What is the topology of a molecule made of fused benzene rings? Hopf and co-workers have examined the case where the benzene rings are fused in an ortho arrangement to complete a circle, the so-called [n]circulenes 1n.1 They computed the series of [3]- to [20]circulene at B3LYP/6-31G(d).
|
|
The most common examples of this class are corannulene 15 and coronene 16. Hopf finds that the small circulenes, [3]- through [6]circulene, are bowls, consistent with many previous studies.
|
|
|
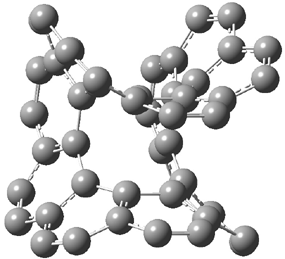
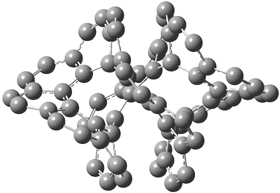
The larger circulenes fall into two distinct topological categories. [7]circulene through [16]circulene are saddles, as shown in Figure 1a. When the compounds are even larger, namely [17]- through [20]circulene, they adopt a helical topology, as seen in Figure 1b. Unfortunately, Hopf does not supply the optimized geometries; there is no supporting material at all. So I have reoptimized [12]circulene at B3LYP/6-31G(d) and [18]circulene at AM1. It is a real shame that authors do not routinely deposit their structures, that referees do not call out the authors on this, and that editors of journals do not demand full geometrical descriptions of all reported computed structures.
|
a) |
b) |
|
112: [12]circulene |
118: [18]circulene |
Figure 1. Optimized structures of (a) [12]circulene (B3LYP/6-31G(d)) and (b) [20]circulene (AM1).
Note the hydrogens have been omitted for clarity.
Hopf does not provide a comparison of structures and their energies. For example, what is the energy difference between the bowl and saddle topologies of [7]circulene or the energy difference between the saddle and helical topologies of [17]circulene?
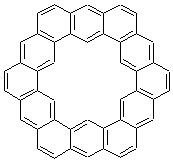
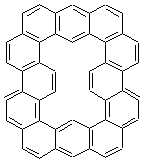
The change in topology of the circulenes is fascinating. One wonders if this change is strictly a function of a stringing fused hexagons in a circle and minimizing the surface. Or is their some π-π stacking that leads to the saddle and helical topologies? Further details would be interesting – as would be examining other types of ciculenes as hinted by the authors at the end of the paper regarding isomeric kekulenes 2.
|
Scheme 1 – examples of kekulenes 2 |
|
|
|
|
References
(1) Christoph, H.; Grunenberg, J.; Hopf, H.; Dix, I.; Jones, P. G.; Scholtissek, M.; Maier, G., "MP2 and DFT Calculations on Circulenes and an Attempt to Prepare the Second Lowest Benzolog, [4]Circulene," Chem. Eur. J. 2008, 14, 5604-5616, DOI: 10.1002/chem.200701837
InChIs
15: InChI=1/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey: VXRUJZQPKRBJKH-UHFFFAOYAF
16: InChI=1/C24H12/c1-2-14-5-6-16-9-11-18-12-10-17-8-7-15-4-3-13(1)19-20(14)22(16)24(18)23(17)21(15)19/h1-12H
InChIKey: VPUGDVKSAQVFFS-UHFFFAOYAQ
112: InChIKey: FTLFLCQEVCSDMZ-UHFFFAOYAB
118: InChIKey: CRXJHICCESJVIG-UHFFFAOYAJ

Computational Organic Chemistry » Quadrannulene responded on 01 Feb 2010 at 9:42 am #
[…] is a four-member ring with four fused-phenyl rings, forming the very small circulene (see this earlier post on circulenes). One might write other resonance structures for the molecule, which could include a central […]
Computational Organic Chemistry » [8]circulene responded on 03 Sep 2013 at 1:31 pm #
[…] can also be named [5]circulene and coronene is [6]circulene. In a previous post I discussed the topology of the circulenes. This earlier work suggested that [8]annulene 1 would have a saddle-shape. This hypothesis has now […]
Computational Organic Chemistry » Curved Aromatic molecules – 4 new examples responded on 24 Sep 2018 at 6:24 am #
[…] second paper presents 4, a non-planar aromatic based on [8]circulene 6.3 (See this post for a general study of circulenes.) [8]circulene has a tub-shape, but is flexible and can undergo tub-to-tub inversion. The expanded […]