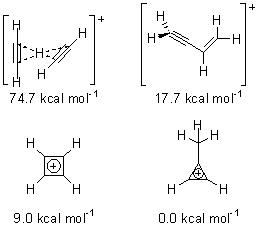
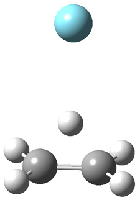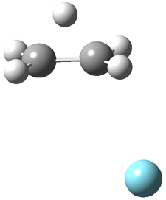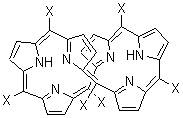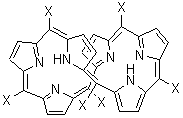The importance of the interactions between neighboring aromatic molecules cannot be overemphasized – π-π-stacking is invoked to explain the structure of DNA, the hydrophobic effect, molecular recognition, etc. Nonetheless, the nature of this interaction is not clear. In fact the commonly held notion of π-π orbital overlap is not seen in computations.

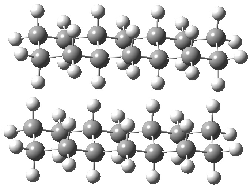
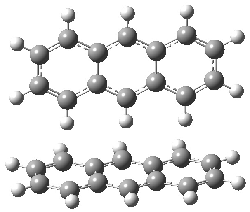
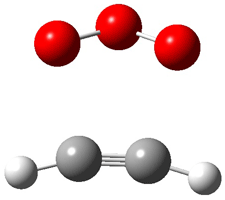
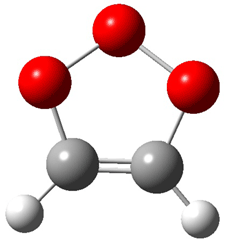
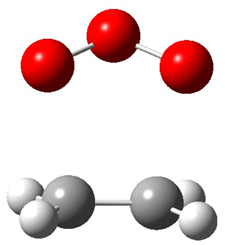
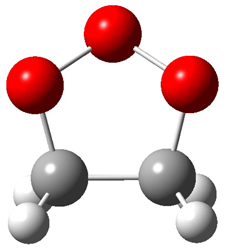
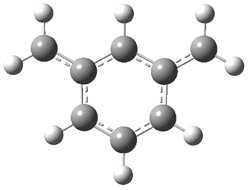
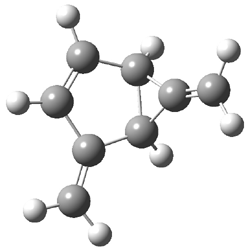
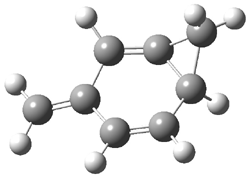
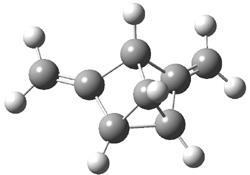
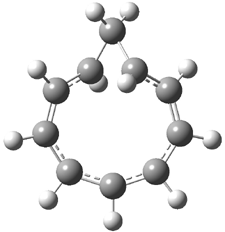
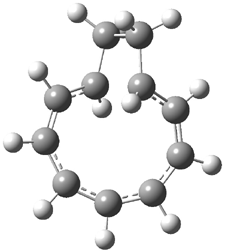
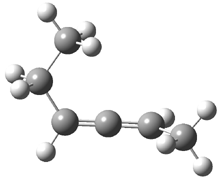
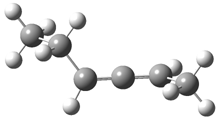
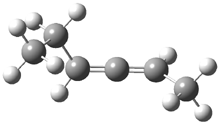
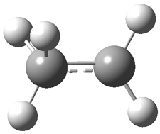
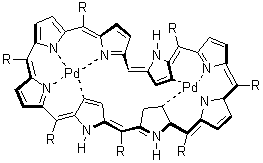
Grimme¹ has now carefully examined the nature of aromatic stacking by comparison with aliphatic analogues. He has examined dimers formed of benzene 1, naphthalene 2, anthracene 3, and teracene 4 and compared these with the dimers of their saturated analogues (cyclohexane 1s, decalin 2s, tetradecahydroanthracene 3s, and octadecahydrotetracene 4s. The aromatic dimmers were optimized in the T-shaped and stacked arrangements, and these are shown for 3 along with the dimer of 3s in Figure 1. These structures are optimized at B97-D/TZV(2d,2p) – a functional designed for van der Waals compounds. Energies were then computed at B2LYP-D/QZV3P, double-hybrid functional that works very well for large systems.

Figure 1. Optimized structures of 3s, 3t, and 3a.

The energies for formation of the complexes are listed in Table 1. The first interesting result here is that the benzene and naphthalene dimmers (whether stacked or T-shaped) are bound by about the same amount as their saturated analogues. Grimme thus warns that “caution is required to not overestimate the effect of the π system”.

Table 1. Complexation energy (kcal mol^-1)

The two larger aromatics here do show a significantly enhanced complexation energy than their saturated analogues, and Grimme refers to this extra stabilization as the π-π stacking effect (PSE). Energy decomposition analysis suggests that electrostatic interactions actually favor the complexation of the saturated analogues over the aromatics. However, Pauli exchange repulsion essentially cancels the electrostatic attraction for all the systems, and it is dispersion that accounts for the dimerization energy. Dispersion increases with size of the molecule, and “classical” dispersion forces (the R^-6 relationship) accounts for more than half of the dispersion energy in the saturated dimmers, while it is the non-classical, or orbital-based, dispersion that dominates in the stacked aromatic dimmers. Grimme attributes this to “special nonlocal electron correlations between the π electrons in the two fragments at small interplane distances”.

References

(1) Grimme, S., "Do Special Noncovalent π-π Stacking Interactions Really Exist?," Angew. Chem. Int. Ed., 2008, 47, 3430-3434, DOI: 10.1002/anie.200705157.

InChIs

1: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H

1s: InChI=1/C6H12/c1-2-4-6-5-3-1/h1-6H2

2: InChI=1/C10H8/c1-2-6-10-8-4-3-7-9(10)5-1/h1-8H

2s: InChI=1/C10H18/c1-2-6-10-8-4-3-7-9(10)5-1/h9-10H,1-8H2

3: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H

3s: InChI=1/C14H24/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h11-14H,1-10H2

4: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

4s: InChI=1/C18H30/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h13-18H,1-12H2

Duncan and Schleyer¹ have investigated protonated acetylene and the protonated acetylene dimer. These ions are created in a pulsed supersonic nozzle/pulsed electrical discharge with a weakly bound argon atom as a tag. IR laser photodissociation spectroscopy allows for the detection of peaks down to 2000 cm^-1, a region not previously explored for this cation. The experimental IR spectrum for H⁺(C₂H₂)^.Ar has two main features: at 3146 and 2217 cm^-1. The 3146 cm^-1 corresponds to the previously observed peak² at 3142 cm^-1 and is similar to the absorption in acetylene (3136 cm^-1). MP2/6-311+G(2d,2p) computations were performed on the classical and non-classical structures of H⁺(C₂H₂), with and without a complexed argon atom. These geometries are displayed in Figure 1 and the predicted vibrational frequencies are listed in Table 1.

Figure 1. MP2/6-311+

Table 1. Relative energies (kcal mol^-1) and frequencies of protonated acetylene
and the protonated acetylene-argon cluster.¹

The argon tag only slightly perturbs the spectrum, as expected for a weakly bond atom remote from most of the hydrogen atoms. The predicted spectra of the two non-classical ions are in nice agreement with the experiment – particularly the interesting peak at 2123 cm^-1 that is due to the bridged proton. This spectra, and the confirmation of the bridging, non-classical structure, makes a nice pair with the recently reported bridging, non-classical structure of the ethyl cation,³ which I blogged on previously.

The spectrum of the H⁺(C₄H₄) ion show a doublet at 3129 and 3158 cm^-1 and two small peaks at 1261 and 1365 cm^-1. The computed structure that comes closest to matching this spectrum is for the asymmetrically bridged dimer (See Figure 2), though is much more energetic than its isomers. The authors speculate that the bridged dimer is trapped in an energy-well during the thermal expansion, which prevents the formation of the lower energy isomers.

Figure 2. Schematic drawing and relative energies of the H⁺(C₄H₄) ion.
(Note – unfortunately the authors have supplied insufficient information in the Supporting Materials to completely define the geometries of these molecules!)

References

(1) Douberly, G. E.; Ricks, A. M.; Ticknor, B. W.; McKee, W.
C.; Schleyer, P. v. R.; Duncan, M. A., "Infrared Photodissociation
Spectroscopy of Protonated Acetylene and Its Clusters," J. Phys. Chem. A, 2008, 112, 1897-1906, DOI: 10.1021/jp710808e.

(2) Gabrys, C. M.; Uy, D.; Jagod, M. F.; Oka, T.; Amano, T., "Infrared Spectroscopy of Carboions. 8. Hollow Cathode Spectroscopy of Protonated Acetylene, C2H3+," J. Phys. Chem., 1995, 99, 15611-15623, DOI: 10.1021/j100042a042.

(3) Andrei, H.-S.; Solcà, N.; Dopfer, O., "IR Spectrum of the Ethyl Cation: Evidence
for the Nonclassical Structure," Angew. Chem. Int. Ed., 2008, 47, 395-397, DOI: 10.1002/anie.200704163

The composite methods (exemplified by the Gaussian-n methods, the Weizmann-n methods and CNS-Q methods) are popularly held to be perhaps the best (if not the most straightforward and mechanical) procedures for obtaining accurate energetics. Errors are generally thought to be in the 1-2 kcal mol^-1 range – quite suitable for comparisons with experiment. The recent study of the 1,3-dipolar cycloaddition of ozone with ethene or ethyne offers serious food for thought about considering these composite methods as simple “black-box” solutions towards obtaining good results.
Wheeler, Ess, and Houk have examined the cycloaddition of ozone with ethyne (Reaction 1) and ethane (Reaction 2) with a variety of different computational techniques.¹ Shown in Figure 1 are the CCSD(T)/cc-pVTZ optimized geometries of the pre-complex, transition state and product for both reactions. One of the potential challenges of these reactions is that ozone has appreciable radical character which is also likely to be true in the pre-complex and transition state but the product should have little to no radical character.

Reaction 1
Precomplex	TS	Product
Reaction 2
Precomplex	TS	Product

The relative enthalphies (0K) of the complex, TS and product were computed using a number of different composite methods. The CBS-QB3, G3, G3B3, G3MP2B3 and G4^2,3 results are listed in Table 1 for both reactions. All of these methods claim a small error – perhaps 1-2 kcal mol^-1. The Gaussian-n methods nicely cluster for the reaction energy for both reactions, while CBS-QB3 predicts both reactions are more exothermic. (The same is also true of CBS-APNO.) The G-n methods indicate that the precomplex is essentially unbound. More concerning is the spread in the enthalpy values of the reaction barrier: the G-n methods predict a barrier that ranges over 5 kcal mol^-1.

Table 1. Relative enthalpies (kcal mol^-1) of the critical points for Reactions 1 and 2.¹

So what is the correct barrier height? A focal point extrapolation procedure was then performed. This seeks to extrapolate to infinite basis set and estimate the effects of correlation through CCSDT(Q) and includes corrections for the Born-Oppenheimer approximation and special relativistic effects. The focal point results are also shown in Table 1. The new G4 composite method gives enthalpies in very nice agreement with those obtained with the much more expensive focal point procedure. However, the other composite methods fair much worse, especially for the activation barrier.
The convergence of the focal point method for the reaction energy is slow, leading to a large error bar of 2 kcal mol^-1. This appears to relate to the radical character difference between the reactant and product. The convergence for the activation barrier is much better (an error of only 0.2 kcal mol^-1) and here the comparison is between reactant and TS which have similar radical character.
Perhaps the most discouraging aspect of this study is that the relative energy predicted using the highest computational component of the composite method – so, CCSD(T)/6-31+G* for the CBS-QB3 method and QCISD(T)/6-31G(d) for the G3 methods – are more accurate than the composite method itself. But, the reasonable performance of the new G4 method^2,3 does offer some glimmer of hope here.

References

(1) Wheeler, S. E.; Ess, D. H.; Houk, K. N., "Thinking
Out of the Black Box: Accurate Barrier Heights of 1,3-Dipolar Cycloadditions of Ozone with Acetylene and Ethylene," J. Phys. Chem. A, 2008, 112, 1798-1807, DOI: 10.1021/jp710104d.

(2) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory," J. Chem. Phys., 2007, 126, 084108, DOI: 10.1063/1.2436888

(3) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory using
reduced order perturbation theory," J. Chem. Phys., 2007, 127, 124105-8, DOI: 10.1063/1.2770701.

InChIs

Reaction 1 product: InChI=1/C2H2O3/c1-2-4-5-3-1/h1-2H

Reaction 2 product: InChI=1/C2H4O3/c1-2-4-5-3-1/h1-2H2

The photochemistry of m-xylylene 2 has been studied by Sander¹ and, as might be anticipated, it’s fascinating! Flash vapor pyrolysis of 1 produces 2. Photolysis of 2 at wavelengths above 400nm gives 3 and 4, while photolysis at 254 nm gives 5. These are products are novel strained hydrocarbons. Confirmation of their structures was obtained by comparing their experimental IR spectra with that computed at B3LYP/6-311G(d,p). Table 1 compares the experimental and computed IR absorptions for 2-5. Note in particular the fine agreement between the two, especially the predicted changes due to i>d₄ substitution for all the phenyl positions.

Table 1. Experimental and Calculated vibrational frequencies (cm^-1) of 2-5.¹

The computed structures of 2-5 and their relative energies are shown in Figure 1. Triplet 1 is the lowest energy isomer, with the singlet-triplet gap of 6.22 kcal mol^-1. This compares with recent high-level computations which give a value of 13.8 kcal mol^-1. ² The other structures are much higher in energy. These other isomers have unusual bonding environments – 3 contains the strained methylenecyclopropane group, 4 is an anti-Bredt compound, and 5 is a very strained tricycle. These compounds can only be prepared by the application of light to provide the energy needed for their creation.

2 Triplet 0.0 Singlet 6.22	3 19.20
4 25.74	5 48.64

Figure 1. B3LYP/6-311G(d,p) optimized structures of 2-5 and their relative energies (kcal mol^-1).¹

References

(1) Neuhaus, P.; Grote, D.; Sander, W., "Matrix Isolation, Spectroscopic Characterization, and Photoisomerization of m-Xylylene," J. Am. Chem. Soc., 2008, 130, 2993-3000, DOI: 10.1021/ja073453d.

(2) Wang, T.; Krylov, A. I., "The effect of substituents on electronic states’ ordering in meta-xylylene diradicals: Qualitative insights from quantitative studies," J. Chem. Phys., 2005, 123, 104304, DOI: 10.1063/1.2018645.

InChIs

2: InChI=1/C8H8/c1-7-4-3-5-8(2)6-7/h3-6H

3: InChI=1/C8H8/c1-5-3-4-7-6(2)8(5)7/h3-4,7-8H,1-2H2; InChIKey=IAJQBWKVTDKBHW-UHFFFAOYAA

4: InChI=1/C8H8/c1-6-2-3-7-5-8(7)4-6/h2-4,7H,1,5H2; InChIKey=XSFFUTQMPAAWHN-UHFFFAOYAU

5: InChI=1/C8H8/c1-3-5-4(2)7-6(3)8(5)7/h5-8H,1-2H2; InChIKey=USZJYFGTTGREFL-UHFFFAOYAB

I know this post is off topic for the blog, but yesterday’s New York Times simply raised my blood pressure.

The Book Review of the New York Times on Sunday March 30 has a review on the book Bonk. The book discusses sex research – and while that certainly is of interest – I want to focus on the associated artwork.

Now chemistry is not usually considered a particularly sexy subject, but its graphics can be fascinating. The periodic table might be the most widely known scientific graphic. The structure of DNA has captured the imagination of more than just scientists. And so it’s not unreasonable that the Times Book Review editors would choose to present some chemical (2-D) drawings. Given the subject of the book, one might have expected perhaps the structures of testosterone and progesterone. Instead, we get the following:

While these structures do not correspond to any known compound – not in and of itself a bad sin – the knowledge (or lack thereof) of chemistry displayed here is simply amazing. The graphic designer is certainly drawn to the preponderance of 6-member rings found in organic chemistry, but has taken this to an extreme! It seems that a random collection of atomic symbols were then willy-nilly added wherever the artist thought would be interesting. The result is simply absurd. One could only have hoped that some copy-editor with a chemistry background could have noticed some of the more glaring mistakes – oh, like five bonds to carbon! For the newspaper of record, these mistakes are simply unwarranted.

To make something good out of this, I am going to hold a contest with my first-semester organic students to identify the errors. The winner will get extra credit in the class – and I will post results here later on.

Here’s another interesting application of computed NMR spectra to resolve the structure of natural products. Braddock and Rzepa have examined obtusallenes V (1), VI (2) and VII (3).¹ The geometries were optimized at mPW1PW91/6-31G(d,p) and the chemical shifts were obtained at this level and using the aug-cc-pVDZ basis set. The larger basis reduces the error and no statistical correction need be applied. The coordinates of these compounds are available through this web-enhanced object of the paper.

The confusion in these structures relates to the position of the halide attachments. For 1 and 2, the problem is which halide (Br or Cl) is at C-7 and C-13. The original structures proposed had these halogens switched from what I’ve drawn, and the correlation between the computed chemical shifts for these original structures and the experiment shows significant deviation: a mean deviation of 1.42 ppm for 1 and 1.67 ppm for 2. Using the structures shown above, along with switching the assigned ¹³C chemical shifts gives much better agreement between the computed and experimental values; the mean deviation is 1.15 ppm for both 1 and 2. Unfortunately the stereochemistry about the allene cannot be determined using NMR – the two different isomers have similar chemical shifts. Similarly, the structure of 3 is predicted as shown above, though the experiment reported only some of the chemical shifts so some uncertainty remains.

References

(1) Braddock, D. C.; Rzepa, H. S., "Structural Reassignment of Obtusallenes V, VI, and VII by GIAO-Based Density Functional Prediction," J. Nat. Prod., 2008, DOI: 10.1021/np0705918.

InChIs

1: InChI=1/C15H18Br3ClO3/c1-8-14(18)12-6-13(17)15(22-12)7-10(19)11(21-15)5-9(20-8)3-2-4-16/h3-4,8-14H,5-7H2,1H3/t2-,8-,9+,10+,11-,12+,13-,14-,15-/m0/s1
InChIKey = PVIUYMGCQVXTIT-JUHTWQEGBT

2: InChI=1/C15H19Br2ClO3/c1-9-14(17)12-4-5-15(20-12)8-11(18)13(21-15)7-10(19-9)3-2-6-16/h3,6,9-14H,4-5,7-8H2,1H3/t2-,9-,10+,11+,12+,13-,14-,15-/m0/s1
InChIKey = WPEZFVRVOYPLJW-LXJGPXSEBA

3: InChI=1/C15H20Br3ClO3/c1-8-15(18)14-6-10(17)13(22-14)7-11(19)12(20)5-9(21-8)3-2-4-16/h3-4,8-15,20H,5-7H2,1H3/t2-,8-,9+,10-,11+,12-,13-,14+,15-/m0/s1
InChIKey = QTZNVLUNNGQAFG-SOAHCKLOBC

A real tour-de-force experimental and computational study of the ORD of 2,3-hexadiene 1 has been produced through the combined efforts of Wiberg, Jorgensen, Crawford, Cheeseman and colleagues.¹ You might not expect a simple compound like 1 to display anything particularly unusual, but you’d be wrong!

2,3-hexadiene exists as three conformations, shown in Figure 1. The cis conformers is the lowest energy form, but the other two are only 0.2 kcal mol^-1 higher in energy, meaning that all three will have significant mol fractions at 0 °C, as listed in Figure 1. The optical rotation for each conformer was determined using B3LYP/aug-cc-pVDZ and CCSD/aug-ccpVDZ. While there is some disagreement in the values determined by the two methods, what is most interesting is that large dependence of [α]_D on the conformation – see Table 1!

cis 0.0 (0.441)

gauche120 0.269 (0.280)

gauche240 0.272 (0.279)

Figure 1. CCSDT optimized geometries of 1, their relative energies (kcal mol^-1) and, in parenthesis, their mol fractions at 0 °C.¹

Table 1. Calculated [α]_D for 1.

^aUsing the aug-ccpVDZ basis set. ^aBoltzman averaged based on the populations shown in Figure 1.

The ORD spectrum of 1 was taken for neat liquid and in the gas phase. The computed and experimental optical rotations are listed in Table 2. Two interesting points can be made from this data. First, the optical activity of 1 is strongly affected by phase. Second, the computed optical rotations, especially the CCSD values, are in fairly good agreement with the gas-phase experimental values.

Table 2. Boltzmann-weighted computed and experimental optical rotations of 1.

A hypothesis to account for the large difference in the gas- and liquid-phase ORD for 1 is that the conformational distribution changes with the phase. The gas and liquid-phase ORD of 2,3-pentadiene shows the same strong phase dependence, even though this compound exists as only one conformer.

Next, a Monte Carlo simulation of gas- and liquid-phase 1 was performed to assess the conformational distributions. Though the range of dihedral angle distributions span about 60°, the population distribution is nearly identical in the two phases – there is no medium-dependence on the conformation distribution, and so this cannot explain the difference in the gas and liquid ORDs.

The authors also tested for the vibrational dependence on the optical rotation. While there is a small correction due to vibrations, it is not enough to account for the differences due to the medium. The origin of this effect remains unexplained.

References

(1) Wiberg, K. B.; Wang, Y. g.; Wilson, S. M.; Vaccaro, P. H.; Jorgensen, W. L.; Crawford, T. D.; Abrams, M. L.; Cheeseman, J. R.; Luderer, M., "Optical Rotatory Dispersion of 2,3-Hexadiene and 2,3-Pentadiene," J. Phys. Chem. A, 2008, DOI: 10.1021/jp076572o.

InChIs

1: InChI=1/C6H10/c1-3-5-6-4-2/h3,6H,4H2,1-2H3/t5-/m1/s1 InChIKey=DPUXQWOMYBMHRN-RXMQYKEDBA

Birney has published another study of a pseudopericyclic reaction to complement the many I discus in Chapter 3.4. Here he looks at that decarbonylation of benzothiophenedione 1, which if analogous to the furandione will first give the ketene 2 before forming 3.¹ Upon gentle heating, 3 dimerizes to 4. Interestingly, 2 has not been detected.²

2 does not exist as a local minimum on the B3LYP/6-31G(d,p) or G3MP2B3 surfaces; rather all optimizations collapse to 3. However, when optimized with PCM with the dielectric of DMSO, 2 is a local minimum.

The transition state for loss of CO from 1 leads directly to 3. This TS (TS1-3, see Figure 1) is non-planar, unlike for the analogous reaction of the furandione. TS1-3 does not correspond with a pseudopericyclic reaction.

TS1-3

TS3-4

Figure 1. B3LYP/6-31G(d,p) optimized geometries of TS1-3 andTS3-4.¹

The transition state for the dimerization of 3 (TS3-4), also shown in Figure 1, appears to be a [2σs + σs] cyclization, which is thermally forbidden. However, analysis of the molecular orbitals indicates the interaction of sets of orthogonal orbitals, exemplary of a pseudopericyclic reaction. The barrier for this reaction, 17.9 kcal mol^-1, is consistent with an allowed pseudopericyclic process.

References

(1) Sadasivam, D. V.; Birney, D. M., "A Computational Study of the Formation and Dimerization of Benzothiet-2-one," Org. Lett., 2008, 10, 245-248, DOI: 10.1021/ol702628v.

(2) Wentrup, C.; Bender, H.; Gross, G., "Benzothiet-2-ones: Synthesis, Reactions, and Comparison with Benzoxet-2-ones and Benzazetin-2-ones," J. Org. Chem., 1987, 52, 3838-3847, DOI: 10.1021/jo00226a022.

InChIs

1: InChI=1/C8H4O2S/c9-7-5-3-1-2-4-6(5)11-8(7)10/h1-4H

2: InChI=1/C7H4OS/c8-5-6-3-1-2-4-7(6)9/h1-4H

3: InChI=1/C7H4OS/c8-7-5-3-1-2-4-6(5)9-7/h1-4H

4: InChI=1/C14H8O2S2/c15-13-9-5-1-3-7-11(9)17-14(16)10-6-2-4-8-12(10)18-13/h1-8H

The structure of the simple, fundamental ethyl cation has finally been ascertained. Computational studies had long suggested the non-classical structure 1 for this cation. The classical structure 2 is a transition state for scrambling the protons. The MP2/6-311G(2d,p) geometries of both structures are shown in Figure 1.

1	2
1.Ar(C2v)	1.Ar(Cs)

Figure 1. MP2/6-311G(2d,f) structures of 1, 2, 1^.Ar(C_2v) and 1^.Ar(C_s).

Dopfer¹ has now obtained IR spectrum of ethyl cation by single-photon IR photodissociation spectroscopy through the reaction

C₂H₅^{+ .} Ar + hν → C₂H₅⁺ + Ar

Two structures of the ethyl cation associated with Ar were optimized at MP2/6-311G(2df,2pd). (The MP2/6-311G(2d,p) structures are shown in Figure 1.) Both of their computed IR spectra have stretches at nearly identical wavenumbers as for ethyl cation 1 itself. The experimental IR spectra has absorptions at 3317 and 3037 cm^-1, very close to the computed frequencies for 1^.Ar(C_2v). This provides strong experimental evidence that ethyl cation is in fact a non-classical ion.

References

(1) Andrei, H.-S.; Solcà, N.; Dopfer, O., "IR Spectrum of the Ethyl Cation: Evidence for the Nonclassical Structure," Angew. Chem. Int. Ed. 2008, 47, 395-397, DOI: 10.1002/anie.200704163

I have discussed Möbius aromatic systems in the book and in the blog. A new Möbius aromatic platform has been synthesized, where the porphyrin π-system is appropriately twisted. Osuka has prepared the hexaphyrins 1 and 2.¹ These possess a double-twist structure, and with its 28 π-electrons 1 should be antiaromatic and 2, having 26 π-electrons should be aromatic.

In fact, the x-ray structure of 1 displays significant bond alternation and the NH protons (in the interior of the molecule) have chemical shift far downfield (δ 14.95 and 12.35 ppm) – all consistent with antiaromatic character. On the other hand¸ while 2 exhibits little bond alternation, the NH protons are seen at 11.1 ppm, too far downfield for the interior positions of an aromatic compound!

Rzepa² has computed 1 and 2 at MPW1PW91/6-31G(d,p) for X=H and CF₃; the latter matches the experimentally prepared compounds. (Rzepa supplies very nice web-enabled access to his results through the supporting materials, and so I do not repeat his structures here. Please also see comments to this post.) As expected, both optimized structures of 1(X=H or X=CF₃) shows distinct bond localization and positive NICS values. The chemical shifts of the NH protons are far downfield, and in reasonable agreement with the experimental shifts. The optimized structures of 2 display bond delocalization and negative NICS values, indicative of aromaticity, as do the NH chemical shifts of 5.2 ppm (X=CF₃) or 3.8 ppm (X=H). These chemical shifts differ from the experiment. Rzepa locates a second less stable conformation 3, but its NH chemical shifts are at 10.9 and 10.1 ppm, in reasonable agreement with experiment. So, he concludes that 1 is antiaromatic and 2 is aromatic and both have a double-twist Möbius topology.

Tanaka, et al have reported the structure of the octaphyrin held in place by a complexed
metal, such as 4.³ A number of analogues have been prepared and their x-ray structure shows the single twist needed for Möbius topology. The NMR spectra are consistent with an aromatic system. And relevant to this blog, B3LYP/6-31G(d) (SDD for the heavy metals) NICS computations reveals a large negative value, -14.6 ppm for 5.

References

(1) Shimizu, S.; Aratani, N.; Osuka, A., "meso-Trifluoromethyl-Substituted
Expanded Porphyrins," Chem. Eur. J., 2006, 12, 4909-4918, DOI: 10.1002/chem.200600158

(2) Rzepa, H. S., "Lemniscular Hexaphyrins as Examples of Aromatic and Antiaromatic
Double-Twist Möbius Molecules," Org. Lett. 2008, DOI: 10.1021/ol703129z

(3) Tanaka, Y.; Saito, S.; Mori, S.; Aratani, N.; Shinokubo, H.; Shibata, N.; Higuchi, Y.; Yoon, Z. S.; Kim, K. S.; Noh, S. B.; Park , J. K.; Kim , D.; Osuka, A., "Metalation of Expanded Porphyrins: A Chemical Trigger Used To Produce Molecular Twisting and Möbius Aromaticity," Angew. Chem. Int. Ed., 2008, 47, 681-684, DOI: 10.1002/anie.200704407

InChIs

1(X=H): InChI=1/C30H22N6/c1-2-20-14-22-5-6-24(33-22)16-26-9-10-28(35-26)18-30-12-11-29(36-30)17-27-8-7-25(34-27)15-23-4-3-21(32-23)13-19(1)31-20/h1-18,31-32,35-36H/b19-13-,20-14-,21-13+,22-14-,23-15-,24-16-,25-15-,26-16-,27-17-,28-18+,29-17-,30-18-

InChIKey: LZQBSNZLFFXDHG-FXYKPCLQBX

1(X=CF₃): InChIKey: XMLQOLTZAIQLSA-UFROFZBYBD

2(X=H): InChI=1/C30H20N6/c1-2-20-14-22-5-6-24(33-22)16-26-9-10-28(35-26)18-30-12-11-29(36-30)17-27-8-7-25(34-27)15-23-4-3-21(32-23)13-19(1)31-20/h1-18,31,36H/b19-13-,20-14-,21-13-,22-14-,23-15-,24-16+,25-15+,26-16-,27-17-,28-18-,29-17-,30-18-

InChIKey: MMFGRQLRZMFRGC-NJRWMLEBBC

2(X=CF₃): InChIKey: FFCNJJQCGZCFGC-FJVZODTDBS