A real tour-de-force experimental and computational study of the ORD of 2,3-hexadiene 1 has been produced through the combined efforts of Wiberg, Jorgensen, Crawford, Cheeseman and colleagues.¹ You might not expect a simple compound like 1 to display anything particularly unusual, but you’d be wrong!

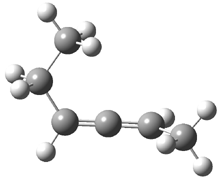
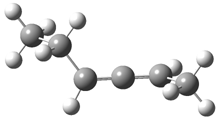
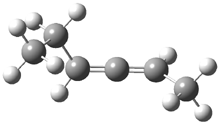
2,3-hexadiene exists as three conformations, shown in Figure 1. The cis conformers is the lowest energy form, but the other two are only 0.2 kcal mol^-1 higher in energy, meaning that all three will have significant mol fractions at 0 °C, as listed in Figure 1. The optical rotation for each conformer was determined using B3LYP/aug-cc-pVDZ and CCSD/aug-ccpVDZ. While there is some disagreement in the values determined by the two methods, what is most interesting is that large dependence of [α]_D on the conformation – see Table 1!

cis 0.0 (0.441)

gauche120 0.269 (0.280)

gauche240 0.272 (0.279)

Figure 1. CCSDT optimized geometries of 1, their relative energies (kcal mol^-1) and, in parenthesis, their mol fractions at 0 °C.¹

Table 1. Calculated [α]_D for 1.

	cis	gauche120	gauche240	averagedb
B3LYP	205.2	415.9	-179.8	156.8
CCSD	208.5	376.7	-120.6	163.8

^aUsing the aug-ccpVDZ basis set. ^aBoltzman averaged based on the populations shown in Figure 1.

The ORD spectrum of 1 was taken for neat liquid and in the gas phase. The computed and experimental optical rotations are listed in Table 2. Two interesting points can be made from this data. First, the optical activity of 1 is strongly affected by phase. Second, the computed optical rotations, especially the CCSD values, are in fairly good agreement with the gas-phase experimental values.

Table 2. Boltzmann-weighted computed and experimental optical rotations of 1.

	Computed		Experiment
nm	B3LYP	CCSD	Liquid	gas
633	134.7	140.6		122
589	156.8	163.8	86.5
546	183.8	203.6	102.0
365	409.7	492.5	243.3
355	427.5	489.3		511

A hypothesis to account for the large difference in the gas- and liquid-phase ORD for 1 is that the conformational distribution changes with the phase. The gas and liquid-phase ORD of 2,3-pentadiene shows the same strong phase dependence, even though this compound exists as only one conformer.

Next, a Monte Carlo simulation of gas- and liquid-phase 1 was performed to assess the conformational distributions. Though the range of dihedral angle distributions span about 60°, the population distribution is nearly identical in the two phases – there is no medium-dependence on the conformation distribution, and so this cannot explain the difference in the gas and liquid ORDs.

The authors also tested for the vibrational dependence on the optical rotation. While there is a small correction due to vibrations, it is not enough to account for the differences due to the medium. The origin of this effect remains unexplained.

References

(1) Wiberg, K. B.; Wang, Y. g.; Wilson, S. M.; Vaccaro, P. H.; Jorgensen, W. L.; Crawford, T. D.; Abrams, M. L.; Cheeseman, J. R.; Luderer, M., "Optical Rotatory Dispersion of 2,3-Hexadiene and 2,3-Pentadiene," J. Phys. Chem. A, 2008, DOI: 10.1021/jp076572o.

InChIs

1: InChI=1/C6H10/c1-3-5-6-4-2/h3,6H,4H2,1-2H3/t5-/m1/s1 InChIKey=DPUXQWOMYBMHRN-RXMQYKEDBA