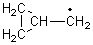A review of my book Computational Organic chemistry written by Christian Mück-Lichtenfeld, has appeared in Synthesis DOI: 10.1055/s-2008-1080541. A few things I particularly appreciate in the review is that Dr. Mück-Lichtenfeld recognized that the book in not intended to be a comprehensive review of computational organic chemistry but rather a survey of highlights, he mentions the book’s web site and blog, and favorably comments on the interviews that conclude each section.
Proton transfer in a hydrated anion
What happens when anions are sequentially solvated with more and more water? In an interesting study by Chesnovsky, Gerber and coworkers, the answer is proton transfer!1 They examined the conjugate base of aniline (C6H5NH–, 1) using both PES and MP2/DZP computations. The PES spectrum of 1 shows two strong peaks. When this anion is then coordinates with one or two water molecules, C6H5NH–).(H2O) or (C6H5NH–).(H2O)2, the peaks shifts to higher energy but the general shape remains unchanged. When three or more water molecules are coordinated to 1, the PE spectra totally changes, becoming broad and relatively featureless.
What accounts for this different PES? The authors posit that the PES of these larger clusters resembles that of hydrated OH– clusters. Optimization of (C6H5NH–).(H2O) or (C6H5NH–).(H2O)2
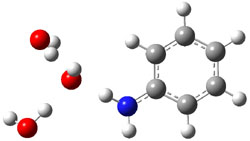
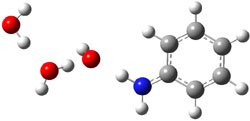
gave structures of the waters hydrogen bonded to the nitrogen anion. However, optimization of the (C6H5NH–).(H2O)3 gave in fact a cluster of the form (C6H5NH2).(HO–).(H2O)2. The two lowest energy structures are shown in Figure 1. The structures correspond to the transfer of one proton from water to the anilinide anion to give aniline associated with hydroxide and two water molecules.
|
Rel E: 0.0 |
Rel E: 0.10 eV |
Figure 1. B3LYP/6-31+G(d) optimized structures of
the C6H5NH2).(HO–).(H2O)2 clusters.
(Note: Once again the authors have failed to include the computed structures as part of the supporting information and so I have reoptimized the structures but at a lower, computationally more tractable level. Hopefully, authors, editors and reviewers will standardize this practice and include such materials in all papers in the very near future!)
Though aniline is a stronger gas-phase acid than water (DPE(aniline) = 366.4 kcal mol-1 and DPE(H2O) = 390.3 kcal mol-1), the reverse is true in solution (pKa(aniline) = 27.3) and pKa(water) = 15.7). As more water molecules are present, the preferential solvation of the hydroxide anion over C6H5NH– results in the formation of hydroxide.
References
(1) Wolf, I.; Shapira, A.; Giniger, R.; Miller, Y.; Gerber, R. B.; Cheshnovsky, O., "Critical Size for Intracluster Proton Transfer from Water to an Anion," Angew. Chem. Int. Ed., 2008, DOI: 10.1002/anie.200800542
Review of SM8
Cramer and Truhlar1 have published a nice review of their SM8 approach to evaluated solvation energy. Besides a quick summary of the theoretical approach behind the model, they detail a few applications. Principle among these is (a) the very strong performance of SM8 relative to some of the standard approaches in the major QM codes (see my previous blog post), (b) modeling interfaces, and (c) computing pKa values of organic compounds.
References
(1) Cramer, C. J.; Truhlar, D. G., "A Universal Approach to Solvation Modeling," Acc. Chem. Res. 2008, 41, 760-768, DOI: 10.1021/ar800019z.
SN2 and E2 DFT benchmark
Bickelhaupt has reported a broad benchmark study of the prototype SN2 and E2 reactions.1 These are the reactions of ethyl fluoride with fluoride and ethyl chloride with chloride (Scheme A). The critical points were optimized at OLYP/TZ2P and then CCSD(T)/CBS energies are used as benchmark. A variety of different density functionals were then used to obtain single-point energies.
Scheme A
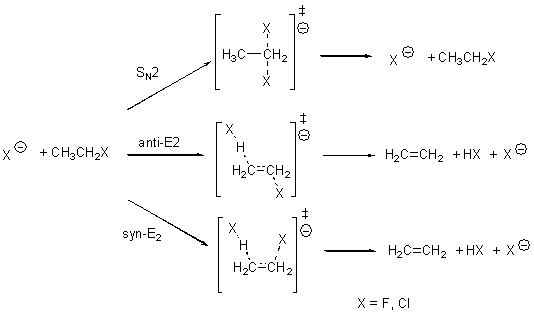
The relative energies of the transition states for the six different reactions are listed for some of the functionals in Table 1. (These are energies relative to separated reactants – and keep in mind that an ion dipole complex is formed between the reactants and the transition states – Bickelhaupt calls this a “reaction complex”.)
Table 1. Relative energies (kcal mol-1) of the transition states for the six reactions shown in Scheme A.
|
|
||||||
|
|
F- |
Cl- |
||||
|
Method |
SN2 |
E2 anti |
E2 syn |
SN2 |
E2 anti |
E2 syn |
|
CCSD(T) |
2.20 |
-1.27 |
5.68 |
5.81 |
18.18 |
30.92 |
|
BLYP |
-11.27 |
-11.55 |
-8.66 |
-3.69 |
5.28 |
14.04 |
|
PW91 |
-11.39 |
-9.58 |
-9.29 |
-3.24 |
6.38 |
14.22 |
|
PBE |
-10.73 |
-9.36 |
-8.98 |
-2.43 |
6.85 |
14.75 |
|
B3LYP |
0.24 |
-5.38 |
-2.00 |
0.92 |
11.00 |
21.22 |
|
MO5-2X |
3.97 |
0.99 |
3.85 |
6.84 |
12.58 |
28.46 |
|
MO6-2X |
5.82 |
1.49 |
4.03 |
10.73 |
10.65 |
30.29 |
|
|
||||||
There is a lot more data in this paper, along with a summary of the mean absolute errors in the overall and central barriers that mimics the data I show in Table 1. The trends are pretty clear. Generalized gradient approximation (GGA) functions – like BLYP, PW91, and PBE – dramatically underestimate the barriers. The hybrid functionals perform much better. The recently maligned B3LYP functional gets the correct trend and provides reasonable estimates of the barriers. Truhlar’s MO5-2X and MO6-2X functionals do very well in matching up the barrier heights along with getting the correct trends in the relative barriers. Simply looking for the functional with the lowest absolute error is not sufficient; BHandH and MO6-L have small errors but give a wrong trend in barriers, predicting that the SN2 reaction is preferred over the E2 for the fluoride reaction.
Reference
(1) Bento, A. P.; Sola, M.; Bickelhaupt, F. M., "E2 and SN2 Reactions of X– + CH3CH2X (X = F, Cl); an ab Initio and DFT Benchmark Study," J. Chem. Theory Comput., 2008, 4, 929-940, DOI: 10.1021/ct700318e.
Dihydrodiazatetracene: is it antiaromatic?
Schleyer continues his study of aromaticity with a paper1 that picks up on the theme presented in one2 I have previously blogged on – the relationship between a formally aromatic pyrazine and formally antiaromatic dihydropyrazine. He now examines the diazotetracene 1 and it dihydro analogue 2.1 In terms of formal electron count, 1 should be aromatic, just like the all carbon analogue tetracene 3, and 2 should be antiaromatic.
Schleyer used the NICSπzz values obtained in the center of each ring to evaluate the aromatic/antiaromatic character of these three molecules. These calculations were performed using canonical molecular orbitals and repeated using localized molecular orbitals. The results are similar for each method, and the canonical MO values are presented in Table 1. As expected for an aromatic compound, each ring of tetracene 3 has large negative NICS values, indicating that each ring is locally aromatic and the molecule as a whole is aromatic. The same is true for the diazotetracene 1. (In fact the NICS values for 1 and 3 are remarkably similar.) However, for 2, the dihydropyrazine ring has a positive NICS values, indicative of a locally antiaromatic ring. While the three phenyl rings have negative NICS values, these absolute values are smaller than for the rings of 1 or 3, indicating an attenuation of their aromaticity. Nonetheless, the sum of the NICS values of 2 is negative, suggesting that the molecule is globally aromatic, though only marginally so. This is due to the antiaromaticity of the dihydropyrazine ring being delocalized to some extent over the entire molecule. Schleyer, concludes that “large 4n π compounds […] are not appreciably destabilized relative to their 4n+2 π congeners.”
Table 1 NICSπzz (ppm) for each ring of 1-3 and their sum.1
|
|
||||
|
-30.0 |
-42.5 |
-41.1 |
-30.1 |
sum = -144.0 |
|
|
||||
|
-26.3 |
-14.2 |
31.3 |
-16.7 |
sum = -25.9 |
|
|
||||
|
-29.6 |
-42.1 |
-42.1 |
-29.6 |
Sum = -143.4 |
References
(1) Miao, S.; Brombosz, S. M.; Schleyer, P. v. R.; Wu, J. I.; Barlow, S.; Marder, S. R.; Hardcastle, K. I.; Bunz, U. H. F., "Are N,N-Dihydrodiazatetracene Derivatives Antiaromatic?," J. Am. Chem. Soc., 2008, 130, 7339-7344, DOI: 10.1021/ja077614p.
(2) Miao, S.; Schleyer, P. v. R.; Wu, J. I.; Hardcastle, K. I.; Bunz, U. H. F., "A Thiadiazole-Fused N,N-Dihydroquinoxaline: Antiaromatic but Isolable," Org. Lett. 2007, 9, 1073-1076, DOI: 10.1021/ol070013i
InChIs
1: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H
2: InChI=1/C16H10N2/c1-2-6-12-10-16-15(9-11(12)5-1)17-13-7-3-4-8-14(13)18-16/h1-10H
3: InChI=1/C16H12N2/c1-2-6-12-10-16-15(9-11(12)5-1)17-13-7-3-4-8-14(13)18-16/h1-10,17-18H
Circulenes
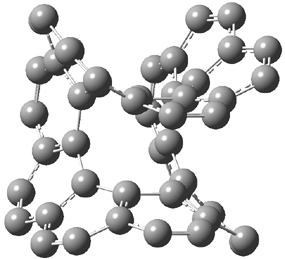
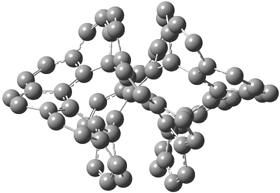
What is the topology of a molecule made of fused benzene rings? Hopf and co-workers have examined the case where the benzene rings are fused in an ortho arrangement to complete a circle, the so-called [n]circulenes 1n.1 They computed the series of [3]- to [20]circulene at B3LYP/6-31G(d).
|
|
The most common examples of this class are corannulene 15 and coronene 16. Hopf finds that the small circulenes, [3]- through [6]circulene, are bowls, consistent with many previous studies.
|
|
|
The larger circulenes fall into two distinct topological categories. [7]circulene through [16]circulene are saddles, as shown in Figure 1a. When the compounds are even larger, namely [17]- through [20]circulene, they adopt a helical topology, as seen in Figure 1b. Unfortunately, Hopf does not supply the optimized geometries; there is no supporting material at all. So I have reoptimized [12]circulene at B3LYP/6-31G(d) and [18]circulene at AM1. It is a real shame that authors do not routinely deposit their structures, that referees do not call out the authors on this, and that editors of journals do not demand full geometrical descriptions of all reported computed structures.
|
a) |
b) |
|
112: [12]circulene |
118: [18]circulene |
Figure 1. Optimized structures of (a) [12]circulene (B3LYP/6-31G(d)) and (b) [20]circulene (AM1).
Note the hydrogens have been omitted for clarity.
Hopf does not provide a comparison of structures and their energies. For example, what is the energy difference between the bowl and saddle topologies of [7]circulene or the energy difference between the saddle and helical topologies of [17]circulene?
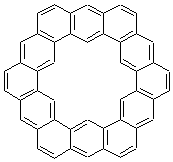
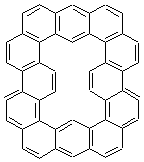
The change in topology of the circulenes is fascinating. One wonders if this change is strictly a function of a stringing fused hexagons in a circle and minimizing the surface. Or is their some π-π stacking that leads to the saddle and helical topologies? Further details would be interesting – as would be examining other types of ciculenes as hinted by the authors at the end of the paper regarding isomeric kekulenes 2.
|
Scheme 1 – examples of kekulenes 2 |
|
|
|
|
References
(1) Christoph, H.; Grunenberg, J.; Hopf, H.; Dix, I.; Jones, P. G.; Scholtissek, M.; Maier, G., "MP2 and DFT Calculations on Circulenes and an Attempt to Prepare the Second Lowest Benzolog, [4]Circulene," Chem. Eur. J. 2008, 14, 5604-5616, DOI: 10.1002/chem.200701837
InChIs
15: InChI=1/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey: VXRUJZQPKRBJKH-UHFFFAOYAF
16: InChI=1/C24H12/c1-2-14-5-6-16-9-11-18-12-10-17-8-7-15-4-3-13(1)19-20(14)22(16)24(18)23(17)21(15)19/h1-12H
InChIKey: VPUGDVKSAQVFFS-UHFFFAOYAQ
112: InChIKey: FTLFLCQEVCSDMZ-UHFFFAOYAB
118: InChIKey: CRXJHICCESJVIG-UHFFFAOYAJ
Heavy atom tunneling
Wes Borden has been exploring reactions where tunneling is operational. These studies have been inspired by Bill Doering’s1 statement regarding tunneling in 1,5-sigmatropic shifts: “The tunneling effect is likely, in the opinion of some, to remain relegated to the virtual world of calculations”. Borden’s first two papers dealt with the kinetic isotope effects for the [1,5]-H shift in 1,3-cyclopentadiene and 5-methyl-1,3-cyclopentadiene.2,3
His latest article examines carbon tunneling,4 which, due to the much heavier mass of the carbon nucleus relative to a proton, is likely to play a minimal role at best. Borden looked at the ring opening of cyclopropylcarbinyl radical 1 to 3-butene-1-yl radical 2, passing through transition state TS1-2. The B3LYP/6-31G(d) optimized structures are shown in Figure 1.
|
|
|
|
|
1 |
TS1-2 |
2 |
Figure 1. B3LYP/6-31G(d) optimized geometries of 1, 2, and TS1-2.4
The predicted rate of the reaction at 298 K using canonical variational transition state theory is increased by about 50% when small-curvature tunneling is included. This predicted rate is a bit smaller than the experimental value. Experiments also shows a linear Arrhenius plot, and Borden’s calculations agree until one reaches very low temperatures. Below 150 K the Arrhenius curve begins to deviate from linearity, and below 20 K the curve is flat – the rate is no longer temperature dependent! Thus, at cryogenic temperatures, the tunneling rate far exceeds traditional crossing of the variational barrier. Borden hopes that experimentalists will reinvestigate this problem (and hopefully confirm his predictions).
References
(1) Doering, W. v. E.; Zhao, X., "Effect on Kinetics by Deuterium in the 1,5-Hydrogen Shift of a Cisoid-Locked 1,3(Z)-Pentadiene, 2-Methyl-10-methylenebicycloJ. Am. Chem. Soc., 2006, 128, 9080-9085, DOI: 10.1021/ja057377v.
(2) Shelton, G. R.; Hrovat, D. A.; Borden, W. T., "Tunneling in the 1,5-Hydrogen Shift Reactions of 1,3-Cyclopentadiene and 5-Methyl-1,3-Cyclopentadiene," J. Am. Chem. Soc., 2007, 129, 164-168, DOI: 10.1021/ja0664279.
(3) Shelton, G. R.; Hrovat, D. A.; Borden, W. T., "Calculations of the Effect of Tunneling on the Swain-Schaad Exponents (SSEs) for the 1,5-Hydrogen Shift in 5-Methyl-1,3-cyclopentadiene. Can SSEs Be Used to Diagnose the Occurrence of Tunneling?," J. Am. Chem. Soc., 2007, 129, 16115-16118, DOI: 10.1021/ja076132a.
(4) Datta, A.; Hrovat, D. A.; Borden, W. T., "Calculations Predict Rapid Tunneling by Carbon from the Vibrational Ground State in the Ring Opening of Cyclopropylcarbinyl Radical at Cryogenic Temperatures," J. Am. Chem. Soc., 2008, 130, 6684-6685, DOI: 10.1021/ja801089p.
InChIs
1: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2
2: InChI=1/C4H7/c1-3-4-2/h3H,1-2,4H2
Electrocyclization of 7-azahepta-1,2,4,6-tetraene
I concluded the subchapter on pseudopericyclic reaction (Chapter 3.4) with a discussion of the controversy concerning the nature of the electrocyclization of 7-azahepta-1,2,4,6-tetraene 1. Quickly summarizing form the book, based on which data one deems important, the reaction can be seen as either pericyclic or pseudopericyclic.
However, I offered David Birney’s opinion as perhaps the proper way to interpret this reaction. David suggested that the TS has both pericyclic and pseudopericyclic character. I wrote that “what we have is a continuum from pericyclic to pseudopericyclic character, analogous to the SN1 to SN2 continuum for nucleophilic substitution”.
Duncan has revisited this reaction,1 employing both B3LYP and CASSCF(10,9) computations. He concludes that the reaction is “neither purely pericyclic nor pseudopericyclic” – just as Birney had indicated. Duncan does offer the possibility of a secondary orbital interaction involving the nitrogen lone pair. But it is nice to see confirmation of the interpretation that David originated for my book!
References
(1) Duncan, J. A.; Calkins, D. E. G.; Chavarha, M., "Secondary Orbital Effect in the Electrocyclic Ring Closure of 7-Azahepta-1,2,4,6-tetraene – A CASSCF Molecular Orbital Study,", J. Am. Chem. Soc., 2008, 130, 6740-6748, DOI: 10.1021/ja074402j.
InChIs
1: InChI=1/C6H7N/c1-2-3-4-5-6-7/h3-7H,1H2/b5-4-,7-6+
InChIKey=VCEMZTODUGWAPF-SCFJQAPRBS
2: InChI=1/C6H7N/c1-6-4-2-3-5-7-6/h2-5,7H,1H2
InChIKey=JGSLKNWXPRDWBA-UHFFFAOYAH
Hexacoordinate carbon
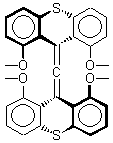
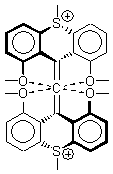
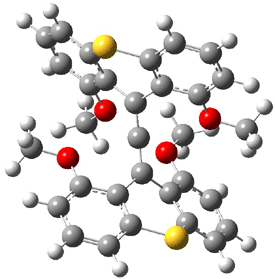
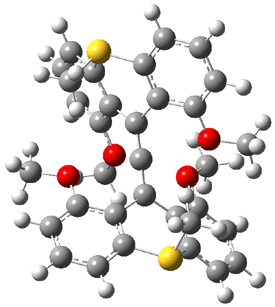
The search for the elusive hypervalent carbon atom took an interesting turn for the positive with the report of the synthesis and characterization of 1 and especially its dication 2.1 The x-ray structure was obtained for both compounds along with computing their B3PW91/6-31G(d) geometries. These computed geometries are shown in Figure 1.
|
|
|
|
1 |
2 |
Figure 1. B3PW91/6-31G(d) optimized geometries of 1 and 2.1
The allene fragment is bent in both structures: 168.5° (169.9° at B3PW91) in 1 and 166.8° (172.7° at B3PW91) in 2. The distances between the central carbon atom of the allene and the four oxygen atoms are 2.66 to 2.82 Å, and computed to be a little longer. Interestingly, these distance contract when the dication 2 is created; ranging from 2.64 to 2.75 Å (again computed to be a little longer). These distances, while significantly longer than normal covalent C-O bonds, are less than the sum of the C and O van der Waals radii. But are they really bonds?
This is not a trivial answer to solve. The authors opt to employ topological electron density analysis (Bader’s atoms-in-molecules approach). Using the electron density from both the high resolution x-ray density map and from the DFT computations, bond paths between the central allene carbon and each oxygen are found, though with, as expected, low values of ρ. The Laplacian of the density at the critical point are positive, indicative of ionic interactions. So according to Bader’s model, the existence of a bond path in a ground state molecule is the necessary and sufficient condition for bonding.
The others conclude by proposing that O…C intermolecular interactions with separations of around 2.6 to 2.8 Å may also suggest hypervalent cases. They note that about 2000 structures in the Cambridge crystallographic database fit this criterion.
References
(1) Yamaguchi, T.; Yamamoto, Y.; Kinoshita, D.; Akiba, K.-y.; Zhang, Y.; Reed, C. A.; Hashizume, D.; Iwasaki, F., "Synthesis and Structure of a Hexacoordinate
Carbon Compound," J. Am. Chem. Soc., 2008, 130, 6894-6895, DOI: 10.1021/ja710423d.
InChIs
1: InChI=1/C31H24O4S2/c1-32-20-9-5-13-24-28(20)18(29-21(33-2)10-6-14-25(29)36-24)17-19-30-22(34-3)11-7-15-26(30)37-27-16-8-12-23(35-4)31(19)27/h5-16H,1-4H3
InChiKey= RJBVLFYVIBCWKW-UHFFFAOYAD
2: InChI=1/C33H30O4S2/c1-34-22-11-7-15-26-30(22)20(31-23(35-2)12-8-16-27(31)38(26)5)19-21-32-24(36-3)13-9-17-28(32)39(6)29-18-10-14-25(37-4)33(21)29/h7-18H,1-6H3/q+2
InChIKey= MVHOSIVPHPDYJJ-UHFFFAOYAM
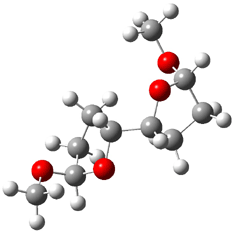
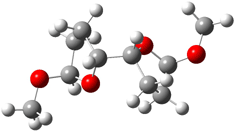
Predicting the 13C NMR of elatenyne
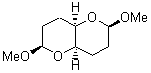
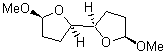
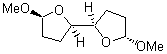
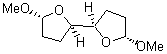
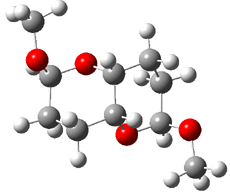
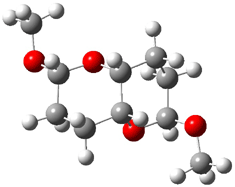
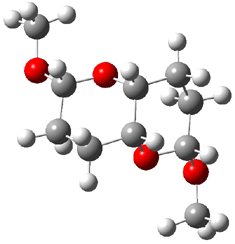
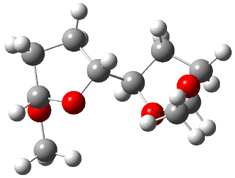
At the Spring ACS meeting in New Orleans this past April, Jonathan Goodman told me about his group’s new work on computed NMR spectra. This study has now appeared.1 The new aspect of this work is taking on compounds with significant conformational flexibility. They first examined the bifuranyl- and pyranopyrans acetals 1-6.
|
|
|
|
|
|
|
|
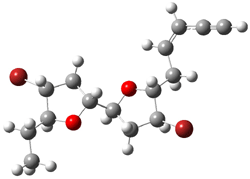
They identified all energetically low-lying conformers through a Monte Carlo MM search, and reoptimized the structures at B3LYP/6-31G**. PCM energies, with the dielectric set to 4.81 to simulate CHCl3, were obtained using the gas-phase geometries. 13C NMR shifts were then computed and weighted based on Boltzmann averaging. Compounds 4-7 require consideration of 4, 5, or 7 conformations, respectively, to account for at least 95% of the population. (The lowest energy conformation for each compound is displayed in Figure 1.) The computed 13C NMR chemical shifts were then compared against the experimental values that have been obtained for 5 of these 6 compounds, though it was not known which experimental spectra corresponds with which structure. Based on the correlation coefficients and the mean and maximum values of the differences between the calculated and experimental shifts allows for identification of the structure that corresponds to each of the five spectra.
|
1 |
2 |
3 |
|
4 |
5 |
6 |
Figure 1. B3LYP/6-31G** minimum energy conformation of 1-6.1
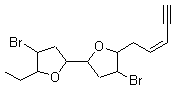
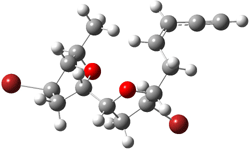
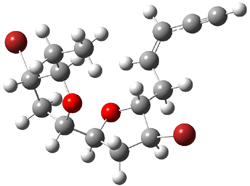
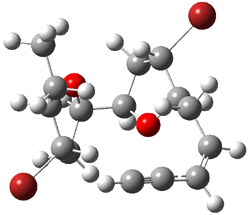
They next took on the absolute structure of elatenyne 7. This compound has been isolated and its 13C NMR obtained nd interpreted.2 The compound can exist in one of 32 different diastereomers. Instead of having to stereospecifically synthesize each diastereomer, obtain its NMR spectra and compare with the natural product, Goodman suggests that one can compute the 13C NMR spectra for each isomer, identified the likely candidates, and synthesize just those if verification is necessary. So, they computed the spectra of all 32 isomers following the above prescription. The chemical shifts for the carbons bearing bromine have relatively large errors, though these can by systematically corrected by reducing the computed values by about 20 ppm. Comparison of the computed spectra of each isomer with the experimental spectra gave three possible isomers (7a-c, see Figure 2) with very strong correlation coefficients. Examination of the men value of the difference of the computed chemical shifts with the experimental values (not including the carbon atoms with a bromine attached) suggests one more possibility 7d (see Figure 2).
|
|
|
|
7a |
7b |
|
7c |
7d |
Figure 2. B3LYP/6-31G** minimum energy conformation of 7a-d.1
References
(1) Smith, S. G.; Paton, R. S.; Burton, J. W.; Goodman, J. M., "Stereostructure Assignment
of Flexible Five-Membered Rings by GIAO 13C NMR Calculations: Prediction of the Stereochemistry of Elatenyne," J. Org. Chem., 2008, DOI: 10.1021/jo8003138.
(2) Sheldrake, H. M.; Jamieson, C.; Burton, J. W., “The Changing Faces of Halogenated Marine Natural Products: Total Synthesis of the Reported Structures of Elatenyne and an Enyne from Laurencia majuscula,” Angew. Chem. Int. Ed., 2006, 45, 7199-7202, DOI: 10.1002/anie.200602211
InChIs
1-3: InChI=1/C10H18O4/c1-11-9-5-3-8-7(13-9)4-6-10(12-2)14-8/h7-10H,3-6H2,1-2H3
4-6: InChI=1/C10H18O4/c1-11-9-5-3-7(13-9)8-4-6-10(12-2)14-8/h7-10H,3-6H2,1-2H3
7: InChI=1/C15H20Br2O2/c1-3-5-6-7-13-11(17)9-15(19-13)14-8-10(16)12(4-2)18-14/h1,5-6,10-15H,4,7-9H2,2H3/b6-5-
InChIKey=SKSTYQSRJPCZSW-WAYWQWQTBQ