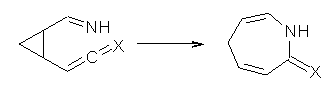
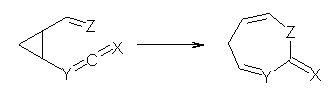
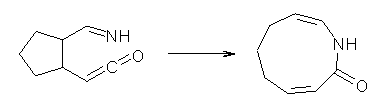
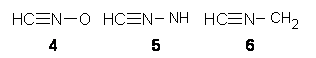Grinberg and colleagues have published a combination of VCD and computation to understand the racemization of imidazoline 1 when exposed to base.¹ Experimental VCD performed at various temperatures indicates first-order kinetics with a barrier of about 24 kcal mol^-1.

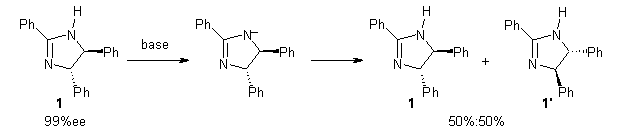
The mechanism for this racemization was proposed and supported with B3LYP/6-31G(d) computations. The anion of 1 can undergo a disrotatory ring opening to form 2, passing through TS1 with a barrier of about 21 kcal mol^-1. Since 2 is chiral with the phenyl groups oriented in non-equivalent positions, ring closure of 2 will go back to 1 and not on to its racemate. In order to racemize, 2 must convert to 3, which can invert to 3’ and then on to 1’. While the barrier for ring opening is likely to be rate limiting, and it does match up reasonably well with the experimental value, the authors have not optimized the transition state that take 2 into 3 or the TS that interconverts 3 with 3’. It’s the former TS that may be pretty large as it requires disruption of the conjugation. Unfortunately, not only have the authors not computed these other TSs, the supplementary materials include only the optimized structure of 1 and not TS1, 2, or 3!

The authors do note that the ring opening is facilitated by the phenyl group on the chiral carbons of 1. They replaced the phenyls with cyclohexyl or cyclohexenyl groups and racemization is no longer observed. Strangely, the authors include in the supporting materials the optimized structures of these variants, but not the TSs for ring opening. Thus, the confirming evidence of a very high barrier for ring opening that would really nail down the mechanism is missing!

References

1) Ma, S.; Busacca, C. A.; Fandrick, K. R.; Bartholomeyzik, T.; Haddad, N.; Shen, S.; Lee, H.; Saha, A.; Yee, N.; Senanayake, C.; Grinberg, N., "Directly Probing the Racemization of Imidazolines by Vibrational Circular Dichroism: Kinetics and Mechanism," Org. Lett., 2010, 12, 2782–2785, DOI: 10.1021/ol100734t

InChIs

1: InChI=1/C21H18N2/c1-4-10-16(11-5-1)19-20(17-12-6-2-7-13-17)23-21(22-19)18-14-8-3-9-15-18/h1-15,19-20H,(H,22,23)/t19-,20-/m0/s1/f/h22H
InChIKey=UCCFUHZMGXEALP-RLNNBPQHDR

A couple of years ago Ess and Houk described computations on the cycloaddition reactions of ethene and ethyne with 9 different 1,3-dipoles 1-9.^1,2 Two interesting results were noted: (a) though barrier heights systematically decreased with the decreasing HOMO-LUMO gap of the 1,3-dipole, the reaction barriers are the same for a given dipole with either ethane or ethyne; (b) The TS geometries about the ethane and ethyne fragments are similar, even though the reactions are quite different in overall reaction energies. This implies a violation of the Hammond Postulate.

Ess and Houk suggested that what dictated these reactions were the energies of distortion of the 1,3-dipole. This is the energy needed to distort the 1,3-dipole into its geometry in the TS. This is typically associated with the bending about the central atom, but rehybridization at the
terminal positions is also needed in many cases. A plot of the distortion energy against the activation barrier gives a line with an R² value of 0.97.

Now Braida, Hiberty and coworkers have employed valence bond computations to interpret these findings.³ The 1,3-dipoles are composed of three valence bond structures a, b and c (shown for 1 below). The last structure (c) is the one associated with the cycloaddition reaction, as it is set up for making the two new bonds at the terminal positions.

The coefficients associated with these VB structures are given in Table 1. It is readily apparent that the degree of diradical character varies considerably among these compounds. Furthermore, for each set of 1,3-dipoles, increasing diradical content correlates with a decreased activation barrier. They also note a strong correlation of decreasing energy needed to excite the ground state 1,3-dipole to the diradical structure (of either the ground state geometry or in the TS geometry) with decreasing activation barrier. Thus, they conclude that it is the diradical character of the 1,3-dipole that controls the reaction – greater diradical character translates into a lower barrier. They argues that the concerted reaction proceeds in two phases, the first phase is distortion of the 1,3-dipole to create sufficient diradical character, and a second phase where the new bonds are made to the dipolarophile, independent of just what that dipolarophile happens to be.

Table 1. Coefficients of the 3 valence bond structures a-c for the ground state 1,3-dipoles 1-9.

References

(1) Ess, D. H.; Houk, K. N., "Distortion/Interaction Energy Control of 1,3-Dipolar
Cycloaddition Reactivity," J. Am. Chem. Soc., 2007, 129, 10646-10647, DOI: 10.1021/ja0734086

(2) Ess, D. H.; Houk, K. N., "Theory of 1,3-Dipolar Cycloadditions: Distortion/Interaction and Frontier Molecular Orbital Models," J. Am. Chem. Soc., 2008, 130, 10187-10198, DOI: 10.1021/ja800009z

(3) Braida, B.; Walter, C.; Engels, B.; Hiberty, P. C., "A Clear Correlation between the Diradical Character of 1,3-Dipoles and Their Reactivity toward Ethylene or Acetylene," J. Am. Chem. Soc., 2010, 132, 7631-7637, DOI: 10.1021/ja100512d

InChIs

1: InChI=1/N2O/c1-2-3
InChIKey=GQPLMRYTRLFLPF-UHFFFAOYAP

2: InChI=1/HN3/c1-3-2/h1H
InChIKey=JUINSXZKUKVTMD-UHFFFAOYAO

3: InChI=1/CH2N2/c1-3-2/h1H2
InChIKey=YXHKONLOYHBTNS-UHFFFAOYAZ

4: InChI=1/CHNO/c1-2-3/h1H
InChIKey=UXKUODQYLDZXDL-UHFFFAOYAL

5: InChI=1/CH2N2/c1-3-2/h1-2H
InChIKey=XILSUYCQFZFDIK-UHFFFAOYAR

6: InChI=1/C2H3N/c1-3-2/h1H,2H2
InChIKey=LSOWAYXKGAQDOG-UHFFFAOYAI

7: InChIInChIKey=DITLKQKHWHCNBT-UHFFFAOYAB

8: InChI=1/CH4N2/c1-3-2/h2-3H,1H2
InChIKey=SSRHHPGUPLMOHA-UHFFFAOYAA

9: InChI=1/C2H5N/c1-3-2/h3H,1-2H2
InChIKey=DASBPRRGHQBNKH-UHFFFAOYAE

What gives rise to the face selectivity in the epoxidation of the alkene of 1 and 2? And why is the epoxidation of 3 of opposite selectivity? Williams¹ argues that the stereoinduction is due to distortional asymmetry, an argument similar to one made recently by Houk^2,3 (see this post) and others for cycloaddition reactions.

The major conclusion from this paper is drawn from the potential energy curve that results from out-of-plane bending of the alkenyl hydrogens, as in Figure 1. The bending curves (computed at B3LYP/6-31g(2d,2p)//B3LYP/6-31+G(d))) are asymmetric: bending the hydrogens away from the three-member ring requires less energy than bending them towards the cyclopropyl ring. However, for 3, bending in the two directions is pretty similar, with a slight preference for bending towards the four-member ring.

Fig. 1 Energy (kcal mol^-1) vs distortion angle of alkenyl hydrogens

This type of bending is part of the distortions that have to occur to reach the transition state, and so Williams argues that the attack from the cyclopropyl face by the oxidant is preferred because of the easier geometric distortion of moving the hydrogen away. Williams makes standard orbital interaction arguments to rationalize the distortion preference.

References

(1) Kolakowski, R. V.; Williams, L. J., "Stereoinduction by distortional asymmetry," Nat. Chem. 2010, 2, 303-307, DOI: 10.1038/nchem.577.

(2)
Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloaddition Reactions of Diazonium Betaines to Acetylene and Ethylene: Bending Vibrations Facilitate Reaction," Angew. Chem. Int. Ed. 2009, 48, 2746-2748, DOI: 10.1002/anie.200805906

(3) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloadditions: Energy Partitioning of Reactants and Quantitation of Synchronicity," J. Am. Chem. Soc., 2010, 132, 3029–3037, DOI: http://dx.doi.org/10.1021/ja909372f

InChIs

1: InChI=1/C9H12/c1-2-7-4-3-6(1)8-5-9(7)8/h1-2,6-9H,3-5H2
InChIKey=YNSKHNKUOPTLCL-UHFFFAOYAA

2: InChI=1/C10H11N/c11-5-8-9-6-1-2-7(4-3-6)10(8)9/h1-2,6-10H,3-4H2
InChIKey=XHTNELKCCFLXEU-UHFFFAOYAJ

3: InChI=1/C10H14/c1-2-8-4-3-7(1)9-5-6-10(8)9/h1-2,7-10H,3-6H2
InChIKey=OYPVZSANECKQOK-UHFFFAOYAR

Rzepa has published a theoretical study of potential stable molecules containing a bond to helium.¹ The work was inspired by the post on this blog pertaining to potential hypervalent carbon species that mimic the S_N2 transition state. Rzepa first reported some of his results on his own blog (see this post and previous ones). The upshot is that structures like 1 appear to possess real bonds to helium!

1

As always, Henry has deposited his structures (see here) and so I have not reproduced any structures.

As an aside I am greatly inspired by this paper as offering an example of how non-traditional media – our two blogs – led to new science, and one that was published by a very forward-thinking publisher (Nature), who recognizes the value of new technologies that facilitate (and not degrade nor supplant) the traditional scientific communication media.

References

1) Rzepa, H. S., “The rational design of helium bonds,” Nature Chem., 2010, 2, 390-393, DOI:10.1038/nchem.596.

Kemnitz and co-workers have added to the protobranching debate (see these earlier posts i, ii, iii) with a proposal for how branching can be stabilizing.¹ A normal chemical bond can be described within the valence bond prescription as an interplay of three different contributors: a covalent term (a) and two ionic terms (b and c). For a typical covalent bond, term a dominates, and for the recently proposed “charge-shift” bond (see this post), the ionic VB terms dominate.

Kemnitz now examines propane using a valence bond method and finds the following. The dominant VB term is the standard, two-covalent bond structure I. Next in importance are the single bond ionic VB structures II. Lastly, the 1,3-ionic structures III contribute about 9% to the total VB wavefunction. These contributions are only possible with branching and provide a net stabilization of about 1.6 kcal mol^-1. This energy is nearly identical to the stabilization energy associated with the protobranching concept proposed by Schleyer, Houk and Mo. This type of ionic structure just might be the mechanism for protobranching stabilization.

References

(1) Kemnitz, C. R.; Mackey, J. L.; Loewen, M. J.; Hargrove, J. L.; Lewis, J. L.; Hawkins, W.
E.; Nielsen, A. F., "Origin of Stability in Branched Alkanes," Chem. Eur. J. 2010, 16,6942-6949, DOI: 10.1002/chem.200902550

Duncan has discovered a pseudopericyclic [3,3]-sigmatropic rearrangement, ¹ and what is particularly interesting is how rare this seems to be! (See this post for an earlier related study.) Using CASSCF/6-31G* computations of Reactions 1-9, only Reaction 1 is found to be pseudopericyclic. (The transition state for this reaction is shown in Figure 1). This characterization is based largely on the shapes of the active MOs, one of which displays two orbital disconnections. In addition, this transition state is much more planar than is typical for a [3,3]-rearrangement. Dihedral angles are about 20 ° in the TS for reaction 1, while in the other reaction TSs, their dihedral angless are about 50 ° or even larger. This is consistent with Birney’s contention that pseudopericyclic reactions have nearly planar TSs. The activation barrier for Reaction 1 is also quite small, 19.4 kcal mol^-1, much lower than for Reactions 2 (26.2 kcal mol^-1) and 3 (33.1 kcal mol^-1).

Figure 1. CASSCF/6-31G* optimized TS for Reaction 1.

References

(1) Forte, L.; Lafortune, M. C.; Bierzynski, I. R.; Duncan, J. A., "CASSCF Molecular Orbital Calculations Reveal a Purely Pseudopericyclic Mechanism for a [3,3] Sigmatropic Rearrangement," J. Am. Chem. Soc., 2010, 132, 2196-2201, DOI: 10.1021/ja906679g

InChIs

Reaction 1:
Reactant (2-(2-methanimidoylcyclopropyl)ethenone):
InChI=1/C6H7NO/c7-4-6-3-5(6)1-2-8/h1,4-7H,3H2
InChIKey=FMPHPBIFFKHFNF-UHFFFAOYAG
Product (1,4-dihydroazepin-7-one):
InChI=1/C6H7NO/c8-6-4-2-1-3-5-7-6/h2-5H,1H2,(H,7,8)/f/h7H
InChIKey=BEYCJMUGQZWVBC-QDQILVOLCK

Since Heilbronner¹ proposed the Möbius annulene in 1964, organic chemists have been fascinated with this structure and many have tried to synthesize an example. I have written many blog posts (1, 2, 3, 4, 5) related to computed Möbius compounds. Now, Herges and Grimme and co-workers have looked at cationic Möbius annulenes.

For the [9]annulene cation,² a variety of DFT methods, along with SCS-MP2 and CCSSD(T) computations suggest that the lowest energy Hückel (1h) and Möbius (1m) structures, shown in Figure 1, are very close in energy. In fact, the best estimate (CCSD(T)/CBS) is that they differ by only 0.04 kcal mol^-1. Laser flash photolysis of 9-chlorobicyclo[6.1.0]nona-2,4,6-triene suggest however that only the Hückel structure is formed, and that its short lifetime is due to rapid electrocyclic ring closure.

In a follow-up study, Herges has examined the larger annulene cations, specifically [13]-, [17]- and [21]-annulenes. ³ The Möbius form of [13]-annulene cation (2m) is predicted to be 11.0 kcal mol^-1 lower in energy that the Hückel (2h) form at B3LYP/6-311+G**. The structures of these two cations are shown in Figure 1. The Möbius cation 2m is likely aromatic, having NICS(0)= -8.95. Electrocyclic ring closure of 2m requires passing through a barrier of at least 20 kcal mol^-1, suggesting that 2m is a realistic target for preparation and characterization.

1h	1m
2h	2m

Figure 1. Optimized structures of 1 (CCSD(T)/cc-pVTZ)² and 2 (B3LYP/6-311+G**)³.

The energy difference between the Möbius and Hückel structures of the larger annulenes is very dependent on computational method, but in all cases the difference is small. Thus, Herges concludes that [13]-annulene cation should be the sole target of synthetic effort toward identification of a Möbius annulene. Experimental studies are eagerly awaited!

References

(1) Heilbronner, E., “Huckel molecular orbitals of Mobius-type conformations of annulenes,” Tetrahedron Lett., 1964, 5, 1923-1928, DOI: 10.1016/S0040-4039(01)89474-0.

2) Bucher, G.; Grimme, S.; Huenerbein, R.; Auer, A. A.; Mucke, E.; Köhler, F.; Siegwarth, J.; Herges, R., "Is the [9]Annulene Cation a Möbius Annulene?," Angew. Chem. Int. Ed., 2009, 48, 9971-9974, DOI: http://dx.doi.org/10.1002/anie.200900886

(3) Mucke, E.-K.; Kohler, F.; Herges, R., "The [13]Annulene Cation Is a Stable Mobius Annulene Cation," Org. Lett., 2010, 12, 1708–1711, DOI: 10.1021/ol1002384

InChIs

1: InChI=1/C9H9/c1-2-4-6-8-9-7-5-3-1/h1-9H/q+1/b2-1-,5-3-,6-4-,9-7-
InChIKey=LIUDWUIEJKKGNI-BWYSQNKRBF

2: InChI=1/C13H13/c1-2-4-6-8-10-12-13-11-9-7-5-3-1/h1-13H/q+1/b2-1-,5-3-,6-4-,9-7-,10-8-,13-11-
InChIKey=FUBPZYTZTJGXKZ-OGBOFXOGBR

Here’s one more attempt to discern the failure of DFT to handle simple alkanes (see this earlier post for a previous attempt to answer this question). Tsuneda and co-workers¹ have employed long-range corrected (LC) DFT to the problem of the energy associated with “protobranching”, i.e., from the reaction

CH₃(CH₂)­_nCH₃ + n CH₄ → (n+1) CH₃CH₃

They computed the energy of this reaction for the normal alkanes propane through decane using a variety of functionals, and compared these computed values with experimentally-derived energies. Table 1 gives the mean unsigned error for a few of the functionals. The prefix “LC” indicated inclusion of long-range corrections, “LCgau” indicates the LC scheme with a gaussian attenuation, and “LRD” indicates inclusion of long-range dispersion.

Table 1. Mean unsigned errors of the “protobranching”
reaction energy of various functional compared to experiment.

A number of important conclusions can be drawn. First, with both LC and LRD very nice agreement with experiment can be had. If only LC is included, the error increases on average by over 1 kcal mol^-1. The MO6-2x functional, touted as a fix of the problem, does not provide complete correction, though it is vastly superior to B3LYP and other hybrid functionals. The authors conclude that the need for LC incorporation points out that the exchange functional lacks the ability to account for this effect. Medium-range correlation is not the main source of the problem as large discrepancies in the reaction energy error occur when different functionals are used that are corrected for LC and LRD. Choice of functional still matters, but LC correction appears to be a main culprit and further studies of its addition to standard functionals would be most helpful.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett. 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

How would you characterized the benzotrithiophene 1? Is it planar? How about when methyl groups are attached (2)? Are these compounds aromatic? A joint computational/experimental study by Wu and Baldridge has tackled these questions.¹

It turns out that both of these compounds are non-planar and have C₂ symmetry. Now, 1 is very nearly planar. But 2 is decidedly non-planar. The MO6-2X/DZ(2d,p) structures are shown in Figure 1. The central 6-member ring has long bonds and expresses some bond alternation: the C-C distance for the bond between the thiophene rings is 1.469 Å and that of the bond shared by the two rings is 1.451 Å The exocyclic bonds are short, 1.375 Å. This appears to be [6]-radialene-like. NICS computations confirm this notion. The NICS(0) value for the central ring of 1 and 2 is -1.6, significantly less negative than the value in benzene of -7.2. The NICS_zz values also reflect non-aromatic character of the central ring. The central ring is non-aromatic.

1

2

Figure 1. MO6-2X/DZ(2d,p) structures of 1 and 2.¹

References

(1) Wu, T.-T.; Tai, C.-C.; Lin, W.-C.; Baldridge, K. K., "1,3,4,6,7,9-Hexamethylbenzo[1,2-c:3,4-c:5,6-c]trithiophene: a twisted heteroarene," Org. Biomol. Chem., 2009, 7, 2748-2755, DOI: 10.1039/b902517k.

InChIs

1: InChI=1/C12H6S3/c1-7-8(2-13-1)10-4-15-6-12(10)11-5-14-3-9(7)11/h1-6H
InChIKey=INZUTJPYADZZEL-UHFFFAOYAI

2: InChI=1/C18H18S3/c1-7-13-14(8(2)19-7)16-10(4)21-12(6)18(16)17-11(5)20-9(3)15(13)17/h1-6H3
InChIKey=WYVKJYPLPAEMLN-UHFFFAOYAA

In order to obtain computed NMR chemical shifts, one computes the isotropic magnetic shielding tensor and subtracts this value from that computed for a reference (or standard) compound. Typically, one uses TMS as the standard. Sarotti and Pellegrinet have questioned whether this is a reasonable approach.¹ Since computational methods vary in quality with methodology, basis set, geometry – one might wonder if the use of a single standard for all computed chemical shifts is the best approach.

They computed the ¹³C chemical shielding tensor for 50 organic compounds possessing a wide variety of functional groups and rings – a few examples are given below. They also computed the ¹³C chemical shielding tensor for 11 different simple organic compounds that might be used as NMR references (like TMS, benzene, methanol, and chloroform).

By comparing the computed chemical shifts obtained using the different references and then matching them with experiment, they propose a multi-reference method. For sp³ carbon atoms they propose using methanol as the reference, and for sp² and sp carbons using benzene as the reference. With chemical shifts computed at mPW1PW91/6-311+G(2d,p)//B3LYP/6-31G(d) using the multi-reference model , the average mean difference from experiment is 2.1 ppm, less than half that found when TMS alone is used. The average RMS deviation of 4.6ppm is about half that when TMS is used as the sole standard.

Though the authors mention the solvent effect on chemical shifts, it is surprising that they did not include solvent in their calculations, especially since they are comparing to experimental chemical shifts in deuterochloroform. Nonetheless, I think this is a nice idea and further exploration of this concept (multi-reference fitting) is worth further pursuits.

References

(1) Sarotti, A. M.; Pellegrinet, S. C., "A Multi-standard Approach for GIAO ¹³C NMR Calculations," J. Org. Chem., 2009, 74, 7254-7260, DOI: 10.1021/jo901234h