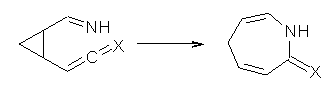
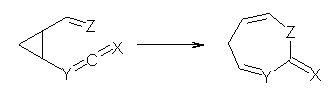
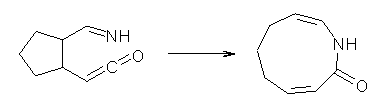
Duncan has discovered a pseudopericyclic [3,3]-sigmatropic rearrangement, 1 and what is particularly interesting is how rare this seems to be! (See this post for an earlier related study.) Using CASSCF/6-31G* computations of Reactions 1-9, only Reaction 1 is found to be pseudopericyclic. (The transition state for this reaction is shown in Figure 1). This characterization is based largely on the shapes of the active MOs, one of which displays two orbital disconnections. In addition, this transition state is much more planar than is typical for a [3,3]-rearrangement. Dihedral angles are about 20 ° in the TS for reaction 1, while in the other reaction TSs, their dihedral angless are about 50 ° or even larger. This is consistent with Birney’s contention that pseudopericyclic reactions have nearly planar TSs. The activation barrier for Reaction 1 is also quite small, 19.4 kcal mol-1, much lower than for Reactions 2 (26.2 kcal mol-1) and 3 (33.1 kcal mol-1).
|
|
Reaction 1: X = O |
|
|
Reaction 4: X = O, Y = CH, Z = CH2 |
|
|
Reaction 8 |
|
|
Reaction 9 |
|
|
Figure 1. CASSCF/6-31G* optimized TS for Reaction 1.
References
(1) Forte, L.; Lafortune, M. C.; Bierzynski, I. R.; Duncan, J. A., "CASSCF Molecular Orbital Calculations Reveal a Purely Pseudopericyclic Mechanism for a [3,3] Sigmatropic Rearrangement," J. Am. Chem. Soc., 2010, 132, 2196-2201, DOI: 10.1021/ja906679g
InChIs
Reaction 1:
Reactant (2-(2-methanimidoylcyclopropyl)ethenone):
InChI=1/C6H7NO/c7-4-6-3-5(6)1-2-8/h1,4-7H,3H2
InChIKey=FMPHPBIFFKHFNF-UHFFFAOYAG
Product (1,4-dihydroazepin-7-one):
InChI=1/C6H7NO/c8-6-4-2-1-3-5-7-6/h2-5H,1H2,(H,7,8)/f/h7H
InChIKey=BEYCJMUGQZWVBC-QDQILVOLCK



Henry Rzepa responded on 10 Jun 2010 at 9:23 am #
The identification of a cyclic reaction as pseudopericyclic is predicated upon identifying one (or in this case) two orbital disconnections. I was trained in the Dewar school of aromaticity, and have always taught pericyclic reactions in this manner; is the transition state aromatic. Unless I missed it, there is no discussion in this article about any NICS value at the centroid of the ring (for reactions with no symmetry,and especially pericyclic reactions, I would use the RCP or ring critical point in the QT-AIM analysis to define this point). Thus this approach (see this blog) identifies surprising aspects of pericyclic reactions which other approaches might miss.
So, does the pseudopericyclic example differ in its NICS value and hence inferred diatropic ring current from the other examples? An orbital disconnection would certainly imply so.
Henry Rzepa responded on 10 Jun 2010 at 1:46 pm #
Might I follow up the previous comment with the suggestion of something far simpler as an explanation for the reaction discussed above;
The N in reaction 1 is the best nucleophile, and the carbonyl of the ketene an excellent electrophile. A simple nucleophilic addition would form either a zwitterionic intermediate, or perhaps an ionic transition state. This would have a substantial dipole moment, and in solution would be heavily stabilized by solvation (even a non polar solvent can do this). In the original article, no mention was made of dipole moments, or the effects of solvent. The modelling was done for the gas phase.

In a blog post I had previously noted how the inclusion of a solvation correction (either continuum or explicit or both) have markedly influence the resulting interpretations. Unless one is modelling a reaction actually conducted in the gas phase, there is no reason at all nowadays why this could not be done routinely.
In this case, we can again invoke William of Occam, in suggesting that the reaction is just a simple nucleophilic addition/elimination, the two steps being either synchronous, or possibly involving a transient dipolar intermediate, but certainly stabilized by solvation. This certainly explains the bond lengths, and the planarity of the transition state. Why invoke anything more complicated? And to answer the question posed in my first comment, the transition state would not be aromatic.