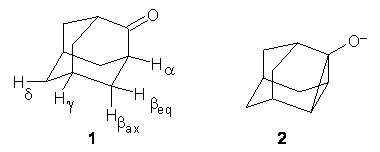
What procedure should one employ when trying to determine a chemical structure from an NMR spectrum? I have discussed a number of such examples in the past, most recently the procedure by Goodman for dealing with the situation where one has the experimental spectra of 2 diastereomers and you are trying to identify the structures of this pair.¹ Now, Goodman provides an extension for the situation where you have a single experimental NMR spectrum and you are trying to determine which of a number of diasteromeric structures best accounts for this spectrum.² Not only does this prescription provide a means for identifying the best structure, it also provides a confidence level.

The method, called DP4, works as follows. First, perform an MM conformational search of every diastereomer. Select the conformations within 10 kJ of the global minimum and compute the ¹³C and ¹H NMR chemical shifts at B3LYP/6->31G(d,p) – note no reoptimizations! Then compute the Boltzmann weighted average chemical shift. Scale these shifts against the experimental values. You’re now ready to apply the DP4 method. Compute the error in each chemical shift. Determine the probability of this error using the Student’s t test (with mean, standard deviation, and degrees of freedom as found using their database of over 1700 ¹³C and over 1700 ¹H chemical shifts). Lastly, the DP4 probability is computed as the product of these probabilities divided by the sum of the product of the probabilities over all possible diastereomers. This process is not particularly difficult and Goodman provides a Java applet to perform the DP4 computation for you!

In the paper Smith and Goodman demonstrate that in identifying structures for a broad range of natural products, the DP4 method does an outstanding job at identifying the correct diastereomer, and an even better job of not misidentifying a wrong structure to the spectrum. Performance is markedly better than the typical procedures used, like using the correlation coefficient or mean absolute error. I would strongly encourage those people utilizing computed NMR spectra for identifying chemical structures to considering employing the DP4 method – the computational method is not particularly computer-intensive and the quality of the results is truly impressive.

Afternote: David Bradley has a nice post on this paper, including some comments from Goodman.

References

(1) Smith, S. G.; Goodman, J. M., "Assigning the Stereochemistry of Pairs of Diastereoisomers Using GIAO NMR Shift Calculation," J. Org. Chem., 2009, 74, 4597-4607, DOI: 10.1021/jo900408d

(2) Smith, S. G.; Goodman, J. M., "Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability," J. Am. Chem. Soc., 2010, 132, 12946-12959, DOI: 10.1021/ja105035r

Somehow I missed this paper when it came out a few months ago, even though I was aware it was coming – as I mentioned it in one of my previous posts!

Anyways, Schreiner and Allen reported on their third study of hydroxyl carbenes (see these posts on dihydroxymethylene and hydroxymethylene), this time examining phenylhydroxycarbene.¹ As I covered in my book, there is a lot of work on phenylcarbenes which typically ring expand to the cycloheptatetraene, see Reaction 1. One might expect phenylhydroxycarbene to do the same thing, i.e. 1 converting into 2 (Reaction 2). 1 is prepared by high-vacuum flash pyrolysis of phenylglyoxylic acid 3 and then capturing the product in an argon matrix at 11 K (Reaction 3).

The carbene 1 is identified through comparison of its experimental and computed (anharmonic frequencies at CCSD(T)/cc-pVDZ) IR frequencies.

No ring expansion is observed at all – Reaction 2 does not occur. Instead, 1 rearranges to benzaldehyde 4 (Reaction 4) at 11 K with a half life of 2.46 h (and a half life of 2.55 h at 20 K). The deuterated analogue does not convert to benzaldehyde and 1-d appears to be completely stable.

So, what is going on? The cis and trans forms of 1 interconvert through a barrier of 22.7 kcal mol^-1. The trans isomer can convert to benzaldehyde (the reaction is very exothermic: -50.8 kcal mol^-1) with a barrier of 28.8 kcal mol^-1 through TS1, shown in Figure 1. The cis isomer can cleave into benzene and CO (not observed) with a huge barrier of 55 kcal mol^-1. All of these barrier were computed at CCSD(T)/cc-pVQZ.

TS1

Figure 1. MP2/cc-pVDZ optimized transition state for the conversion of 1 into 4.

Benzaldehyde seems to be produced by passing through a huge barrier, something that is impossible from a thermal perspective (we’re at 11 K!). But this can be accomplished by tunneling. Tunneling probabilities were computed from the MP2/aug-cc-pVDZ intrinsic reaction path with barrier penetration integrals computed with the WKB approximation. The bottom line: the computed half-life is 3.3 h and the deuterated species is computed to have a half-life of 8700 years(!), both in excellent agreement with experimental observation. Quantum mechanical tunneling is clearly the explanation for this chemistry.

This is another fine example of the power of joint experimental/computational studies. And be on the look-out for an even more exciting case from this group. I met with Wes Allen on my recent trip to the University of Georgia and was entertained with another hydroxycarbene that undergoes quite novel tunneling!

References

(1) Gerbig, D.; Reisenauer, H. P.; Wu, C.-H.; Ley, D.; Allen, W. D.; Schreiner, P. R., "Phenylhydroxycarbene," J. Am. Chem. Soc., 2010, 132, 7273-7275, DOI: 10.1021/ja9107885

InChIs

1: InChI=1/C7H6O/c8-6-7-4-2-1-3-5-7/h1-5,8H
InChIKey=QVZIGMRPQWIGCV-UHFFFAOYAE

2: InChI=1/C7H6O/c8-7-5-3-1-2-4-6-7/h1-6H
InChIKey=QVWDCTQRORVHHT-UHFFFAOYAM

3: InChI=1/C8H6O3/c9-7(8(10)11)6-4-2-1-3-5-6/h1-5H,(H,10,11)/f/h10H
InChIKey=FAQJJMHZNSSFSM-KZFATGLACS

4: InChI=1/C7H6O/c8-6-7-4-2-1-3-5-7/h1-6H
InChIKey=HUMNYLRZRPPJDN-UHFFFAOYAE

It’s been a while since I blogged about the use of computed spectra to determine the structure or configuration of a compound. Well, here’s a nice example of the use of computed electronic circular dichroism to determine the configuration of a coumarin that displays axial chirality.

Mazzanti and coworkers have synthesized a series of coumarins,¹ obtained their ECD and computed their structures, stero-interconversion barriers (at B3LYP/6-31G(d)) and ECD (at TD-DFT/B3LYP/6-311++G(2d,p)//B3LYP/6-31G(d)). I will mention explicitly here just one example, compound 1, which elutes off a chiral column in two mirror image forms, both of which do not stereomutate over time.

The computed structure of 1 is shown in Figure 1 and the barrier for steromutation is predicted to be quite large, 35.7 kcal mol^-1. This explains the lack of stereomutation. The computed ECD of 1M matches very well with the experimental ECD of the first eluted isomer, making the second eluted isomer 1P.

1

Figure 1. B3LYP/6-31G(d) optimized structure of 1.

References

(1) Lunazzi, L.; Mancinelli, M.; Mazzanti, A.; Pierini, M., "Stereomutation of Axially Chiral Aryl Coumarins," J. Org. Chem., 2010, ASAP, DOI: 10.1021/jo101261k

InChIs

1 (6-isopropyl-4-(2-methyl-1-naphthyl)chromen-2-one):
InChI=1/C23H20O2/c1-14(2)17-10-11-21-19(12-17)20(13-22(24)25-21)23-15(3)8-9-16-6-4-5-7-18(16)23/h4-14H,1-3H3
InChIKey=OEQFRNPVUJVJFO-UHFFFAOYAS

The de novo design of catalysts for specific purposes remains an inspired goal for chemists and biochemists. Ken Houk and David Baker have been pursuing this goal, and their recent paper on the design of a catalyst for the bimolecular Diels-Alder¹ is a real significant step forward.

Their model enzyme is one that will provide a hydrogen bond acceptor to the carbamate proton of 1 and a proton donor to the carbonyl oxygen of the amide 2. This model is sketched in Figure 1. Glutamine or asparagines will serve as the acceptor and serine, threonine, or tyrosine will serve as the proton donor. The catalytic site is then modeled, and then this active site is fit within 207 protein scaffolds. About 10¹⁹ active site configurations are reduced to about 10⁶ possible protein scaffolds. Optimization of these led to 84 protein designs.

Figure 1. Enzyme model

These 84 possible proteins were then synthesized within E. coli and then tested for catalytic behavior
in the Diels-Alder reaction of 1 + 2. Only 2 enzymes have activity, and with some protein modifications, quite reasonable enzyme activity is found. These enzymes show strong selectivity for the substrates – addition of a methyl group significantly diminishes catalytic activity. Perhaps most important is that of the 8 possible isomers that can be formed (4 isomers are produced in the uncatalyzed reaction) only 1 is produced here, the 3R,4S isomer 3.

All-in-all, a quite remarkable accomplishment!

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D.,
"Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239.

InChIs

1: InChI=1/C13H13NO4/c1-2-3-8-14-13(17)18-9-10-4-6-11(7-5-10)12(15)16/h2-8H,1,9H2,(H,14,17)(H,15,16)/p-1/b8-3+/fC13H12NO4/h14H/q-1
InChIKey=HGMJQUSLRHRARW-OSXKDGDFDJ

2: InChI=1/C5H9NO/c1-4-5(7)6(2)3/h4H,1H2,2-3H3
InChIKey=YLGYACDQVQQZSW-UHFFFAOYAD

3: InChI=1/C18H22N2O5/c1-20(2)16(21)14-5-3-4-6-15(14)19-18(24)25-11-12-7-9-13(10-8-12)17(22)23/h4,6-10,14-15H,3,5,11H2,1-2H3,(H,19,24)(H,22,23)/p-1/t14-,15+/m0/s1/fC18H21N2O5/h19H/q-1
InChIKey=WWWDBAXWGWLFSD-AFFTYDCXDH

Determination of absolute configuration remains a difficult undertaking, one usually solved by x-ray crystallography. In my book (Chapter 1.6.3) and blog (see these posts) I have noted the use of computations in conjunction with optical rotation or electronic circular dichroism as an alternative: possible configurations are optimized and their optical properties are computed and then matched against experimental spectra.

Neri and coworkers have utilized this approach to determine the absolute configuration of the chiral calix[4]arene 1.¹

Computed optical rotations (TDDFT/B3LYP/6-31G* at 5 frequencies) are compared with experimental values in Table 1. While the magnitude is off (as is typical) the sign of the activity along with the trend matches up very well for the cS configuration shown in Figure 1. It should be noted that a second conformation makes up about 10% of the Boltzmann population, and the contribution of this second configuration is included in the computed values shown in Table 1. In addition, computations at higher levels give very similar results. Lastly, the computed ECD spectrum of the cS isomer also matches up well with experiment.

Table 1. Optical rotation of the cS isomer of 1 compared with experiment

Figure 1. B3LYP/6-31G* optimized structure of the major conformation of 1.

Given the relatively low level of theory employed here, further use of this combined experimental/computational approach to obtaining absolute configurations of large molecules is encouraged.

References

(1) Talotta, C.; Gaeta, C.; Troisi, F.; Monaco, G.; Zanasi, R.; Mazzeo, G.; Rosini, C.; Neri, P., "Absolute Configuration Assignment of Inherently Chiral Calix[4]arenes using DFT Calculations of Chiroptical Properties," Org. Lett., 2010, 12, 2912-2915, DOI: 10.1021/ol101098x

InChIs

1: InChI=1/C59H78O7/c1-16-19-64-53-36-22-35-32-47(59(13,14)15)50(51-48(61)33-45(60)34-49(51)62)46(52(35)63)31-41-30-44(58(10,11)12)29-40(55(41)66-21-18-3)24-39-28-43(57(7,8)9)27-38(54(39)65-20-17-2)23-37(53)26-42(25-36)56(4,5)6/h25-30,32-34,60-63H,16-24,31H2,1-15H3
InChIKey=VGWOVZXMYMCPQO-UHFFFAOYAS

Li and Danishefsky report a study of the Diels-Alder reaction involving cyclobutenone 1 as the dienophile.¹ They claim that “perhaps the ring strain of 1 might well serve to enhance its dienophilicity relative to corresponding cyclopentenones or cyclohexenones.” In fact, 1 is an excellent dienophile, with reactions at or below 0° being accomplished in less than half a day with yields upwards of 90%. The reaction goes with endo selectivity.

What is surprising to me is the statement in the article:

While the magnitude of the effect could not have been predicted in advance, the rate enhancement with 1 must reflect the favorable effects of rehybridization of two particularly strained sp² carbons in the cycloaddition transition state.

Now, Danishefsky alludes to upcoming computations results in a future paper, but I don’t see why the rate enhancement could not have been “predicted in advance”. So, I have optimized the structures of reactants, endo and exo transition states, and products of the reaction of 1,3-butadiene with 1, cyclopentenone 2 and cyclohexenone 3 at B3LYP/6-311G(d) – Reactions 1-3.

The endo TS is preferred for the reaction of 1 and 2, while the endo and exo TSs for 3 are essentially isoenergetic. The optimized geometries are shown in Figure 1.

1TSendo

2TSendo

3TSendo

Figure 1. B3LYP/6-311G(d) optimized geometries of the endo TSs of Reactions 1-3.

The computed activation barriers and overall reaction energies are listed in Table 1. Clearly, the cycloaddition of 1 is favored both in terms of kinetics (having the lowest barrier) and thermodynamically (having the most exothermic reaction energy). In fact, the reaction barriers increases in going from 1 to 2 to 3 and the exothermicity decreases in that same order. This nicely dovetails with the strain energies of the dienophiles and the fact that cyclopententones and cyclohexenones are generally poor dienophiles. Thus, one clearly could have predicted these results in advance!

Table 1. Activation and Reaction Energy (kcal mol^-1) for Reactions 1-3.

Nonetheless, the experimental work is extremely nice and this work offers a new avenue into some interesting bicyclic structures.

Note: This post has been modified to correct the errors in the product structures and their associated InChIs and InChIKeys.

References

(1) Li, X.; Danishefsky, S. J., "Cyclobutenone as a Highly Reactive Dienophile: Expanding Upon Diels-Alder Paradigms," J. Am. Chem. Soc., 2010, 132, 11004-11005, DOI: 10.1021/ja1056888

InChIs

1: InChI=1/C4H4O/c5-4-2-1-3-4/h1-2H,3H2
InChIKey=DFLRGCFWSRELEL-UHFFFAOYAP

1prod: InChI=1/C8H10O/c9-8-5-6-3-1-2-4-7(6)8/h1-2,6-7H,3-5H2/t6-,7-/m0/s1
InChIKey=AYXQRXAAJYZWJJ-BQBZGAKWBC

2: InChI=1/C5H6O/c6-5-3-1-2-4-5/h1,3H,2,4H2
InChIKey=BZKFMUIJRXWWQK-UHFFFAOYAH

2prod: InChI=1/C9H12O/c10-9-6-5-7-3-1-2-4-8(7)9/h1-2,7-8H,3-6H2/t7-,8-/m0/s1
InChIKey=LOJATDUUSCWAOA-YUMQZZPRBU

3: InChI=1/C6H8O/c7-6-4-2-1-3-5-6/h2,4H,1,3,5H2
InChIKey=FWFSEYBSWVRWGL-UHFFFAOYAT

3prod: InChI=1/C10H14O/c11-10-7-3-5-8-4-1-2-6-9(8)10/h1-2,8-9H,3-7H2/t8-,9-/m0/s1
InChIKey=LFDGSLNQYSSFGI-IUCAKERBBQ

The α-proton of ketones and aldehydes are acidic, thanks to delocalization of the resulting anion. However, α-protons at a bridgehead position are much less acidic – the resulting anion is not delocalized as the enolate would be an anti-Bredt alkene. So, what about more remote protons from the carbonyl – would they exhibit enhanced acidity due to inductive or field effects?

Kass has examined the deprotonation of 2-adamantone 1 via experiment and computation.¹ The relative energies of the five different anions are listed in Table 1. Previous H/D exchange experiments indicate that the relative reactivity is β_ax > β_eq > α, and this is well reproduced by computations.²

Table 1. Relative energies (kcal mol^-1) of the enolates of 1.

Kass’ bracketing experiments indicate the enthalpy for deptrotonation of 2-adamantone is 394.7 ± 1.4 kcal mol^-1. This is in nice accord with the computational results for loss of the β_ax proton: 393.8 (M06-2x/aug-cc-pVDZ) and 396.8 kcla mol^-1 (G3). One interesting computational result is a competive cyclic structure 2, whose stability is similar to that to the β_ax ion at M06-2x and is the optimized structure produced at MP2/6-31G(d) when searching for the β_eq enolate.

So, to answer our question, protons remote from a carbonyl are more acidic than alkane
analogues, but much less acidic than typical α-protons of ketones.

References

(1) Meyer, M. M.; Kass, S. R., "Enolates in 3-D: An Experimental and Computational Study of Deprotonated 2-Adamantanone," J. Org. Chem., 2010, 75, 4274-4279, DOI: 10.1021/jo100953y

(2) Stothers, J. B.; Tan, C. T., "Adamantanone: stereochemistry of its homoenolization as shown by ²H nuclear magnetic resonance," J. Chem. Soc., Chem. Commun., 1974, 738-739, DOI: 10.1039/C39740000738

InChI

1: InChI=1/C10H14O/c11-10-8-2-6-1-7(4-8)5-9(10)3-6/h6-9H,1-5H2
InChIKey=IYKFYARMMIESOX-UHFFFAOYAE

2: InChI=1/C10H13O/c11-10-7-2-5-1-6(4-7)9(10)8(10)3-5/h5-9H,1-4H2/q-1
InChIKey=WTXOXRNASCZDME-UHFFFAOYAE

I recently finished reading a book on the application of information theory to “reality”: Decoding Reality by Vlatko Vedral. It’s for the layman (me!) and I was wondering what applications have information theory made in chemistry. Well, just by accident I happened upon a paper by Noorizadeh which proposes an information-based metric to evaluate aromaticity!¹ (I know what you’re thinking – we need another aromaticity metric like we need another hole in the head.) I don’t want to suggest that this metric, which he calls “Shannon aromaticity” after the inventor of information theory, will substitute for previous ones (like aromatic stabilization energy or NICS). But the application here is interesting.

Shannon defined entropy in the information sense as

Where p_i is the probability of occurrence i. This can be converted into a quantum analogue as

Noorizadeh suggests evaluating the electron density at the bond critical points of an aromatic ring and then summing the values of S at each of these ring critical points. An ideal aromatic ring would have S_max= ln (N) where N is the number of bonds in the ring. So, the Shannon aromaticity (SA) is then defined as the difference between the maximum value (ln (N)) and the sum over the ring critical points. A small value would indicate an aromatic ring, and a large value would indicate an antiaromatic ring.

The paper shows a strong correlation exists between the new SA metric and the warhorses ASE and NICS and HOMA for a variety of aromatic, antiaromatic and non-aromatic systems. This new metric is easy to compute and perhaps offers a new way to be thinking about a very old concept: aromaticity.

References

(1) Noorizadeh, S.; Shakerzadeh, E., "Shannon entropy as a new measure of aromaticity, Shannon aromaticity," Phys. Chem. Chem. Phys., 2010, 12, 4742-4749, DOI: 10.1039/b916509f.

Often gem-dialkyl substitution accelerates a reaction, for example in the formation of an epoxide via reaction 1. Here the relative rates are 1:21:252 in going from 1 to 2 to 3.¹ This acceleration is the Thorpe-Ingold effect and had been suggested to arise from a steric reaction: that the methyl groups contract the angle and bring the terminal groups closer together.

1: R₁ = R₂ = H
2: R₁ = Me, R₂ = H
3: R₁ = R₂ = Me

Kostal and Jorgensen² have examined the reaction of the 2-chloroethoxides 1-3 using computations, especially to look at the effect of solvent. At MP2/6-311+G(d,p) and CBS-Q, the relative rates (based on the activation free energy ΔG^‡) are 1:2.8:17 and 1:0.7:3.7, respectively. Evidently there is no significant rate enhancement afforded by gem-substitution in the gas phase.

However, solution computations give a very different result. Using PCM along with the MP2 method, the computed relative rates are 1:5.8:1100 and with the Monte Carlo-Free Energy Perturbation method, the relative rates for aqueous solution are 1:30:773. Thus, the Thorpe-Ingold acceleration is due to solvent. Analysis of the hydrogen bonded structures and the solute-water pair distributions suggest that increasing alkyl substitution reduces the strength of solvation of the reactant, leading to the lower activation barrier.

References

(1) Jung, M. E.; Piizzi, G., "gem-Disubstituent Effect:Theoretical Basis and Synthetic Applications," Chem. Rev., 2005, 105, 1735-1766, DOI: 10.1021/cr940337h

(2) Kostal, J.; Jorgensen, W. L., "Thorpe-Ingold Acceleration of Oxirane Formation Is Mostly a Solvent Effect," J. Am. Chem. Soc., 2010, 132, 8766-8773, DOI: 10.1021/ja1023755

Alder and co-workers have published a substantial theoretical study of potential [6+4]-cycloaddition reactions.¹ There is much too much to summarize from this study, but I highlight here an interesting result that is consistent with one of the themes of the book and blog: unusual potential energy surfaces.

They examined two [6+4]-cycloadditon routes involving 1,3,5-hexatriene with 1,3-butadiene to give 1 and 2. These products are shown in Figure 1. A competing [4+2]-cycloaddition is also possible, giving rise to 3 and 4. Interestingly, only one TS is found leading to 1/3 and one TS leading to 2/4. (These TSs are also shown in Figure 1.) This is reminiscent of many examples from the book and blog where a single TS seems to lead to 2 different products. A valley-ridge inflection point divides the surface between 1 and 3 (VRI-1), and a second valley-ridge inflection point separates 2 from 4 (VRI-2). In addition a Cope transition state (CTS1) takes 1 into 3, and a second TS (CTS2) takes 2 into 4.

TS1	TS2
1	2
CTS1	CTS2

Figure 1. B3LYP/6-31G* optimized structures of the TSs and products of the reaction of 1,3,5-hexadiene with 1,3-butadiene.¹

This type of surface requires study of the dynamics to truly predict what the outcome will be of the reaction. Unfortunately, the low barriers for the Cope rearrangements along with 3 and 4 being much more stable than 1 and 2 indicates that the [6+4] product is unlikely to be observed. Nonetheless, this is yet another example of an unexpected PES.

References

(1) Alder, R. W.; Harvey, J. N.; Lloyd-Jones, G. C.; Oliva, J. M., "Can _π6 + _π4 = 10? Exploring Cycloaddition Routes to Highly Unsaturated 10-Membered Rings," J. Am. Chem. Soc. 2010, 132, 8325-8337, DOI: 10.1021/ja1008135

InChIs

1: InChI=1/C10H14/c1-2-4-6-8-10-9-7-5-3-1/h1-4,9-10H,5-8H2/b3-1-,4-2+,10-9+
InChIKey=RBGHZLIWLPEVLM-OCXPBMDHBA

2: InChI=1/C10H14/c1-2-4-6-8-10-9-7-5-3-1/h1-4,9-10H,5-8H2/b3-1-,4-2-,10-9+
InChIKey=RBGHZLIWLPEVLM-ARMDLRMMBD

3: InChI=1/C10H14/c1-3-9-7-5-6-8-10(9)4-2/h3-5,7,9-10H,1-2,6,8H2/t9-,10-/m0/s1
InChIKey=ANOQDGNLTWJTRB-UWVGGRQHBI

4: InChI=1/C10H14/c1-3-9-7-5-6-8-10(9)4-2/h3-5,7,9-10H,1-2,6,8H2/t9-,10+/m1/s1
InChIKey=ANOQDGNLTWJTRB-ZJUUUORDBZ