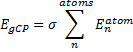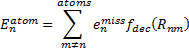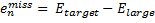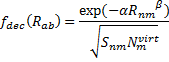Basis set superposition error plagues all practical computations. This error results from the use of incomplete basis sets (thus pretty much all computations will suffer from this problem). The primary example of this error is in the formation of a supermolecule AB from the monomers A and B. Superposition occurs when in the computation of the supermolecule, basis functions centered on B are used to supplement the basis set of A, not to describe the bonding or interaction between the two monomers, but simply to better the description of the monomer A itself. Thus, BSSE always serves to increase the binding in the supermolecule. Recently, this concept has been extended to intramolecular BSSE, as discussed in these posts (A and B).
The counterpoise correction proposed by Boys and Bernardi corrects for the superposition by computing the energy of each monomer using the basis sets centered on both monomers, often referred to as ghost orbitals because the functions are used but not the nuclei upon which they are centered. This can overcorrect for superposition but is the only widely utilized approach to treat the problem. A variation on this approach is what has been suggested for the intramolecular
BBSE problem.
A major discouragement for wider use of counterpoise correction is its computational cost. Kruse and Grimme offer a semi-empirical approach that is extremely cost effective and appears to strongly mimic the traditional counterpoise correction.1
They define the geometric counterpoise scheme (gCP) that provides an energy correction EgCP that can be added onto the electronic energy. This term is defined as
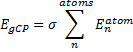
|
Eq. (1)
|
where σ is an empirically fitted scaling term. The atomic contributions are defined as
|
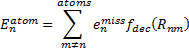
|
Eq. (2)
|
where emiss are the errors in the energy of an atom with a particular target basis set, relative to the energy with some large basis set:
|
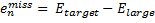
|
Eq. (3)
|
(On a technical matter, the atomic terms are computed in an electric field of 0.6a.u. in order to get some population into higher energy orbitals.) The fdec term is a decay function that relates to the distance between the atoms (Rnm) and the overlap
(Snm):
|
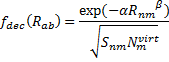
|
Eq. (4)
|
where Nvirt is the number of virtual orbitals on atom m, and α and β are fit parameters. Lastly, the overlap term comes from the integral of a single Slater orbital with coefficient
where ξs and ξp are optimized Slater exponents from extended Huckel theory, and η is the last parameter that needs to be fit.
There are four parameters and these need to be fit for each specific combination of method (functional) and basis set. Kruse and Grimme provide parameters for a number of combinations, and suggest that the parameters devised for B3LYP are suitable for other functionals.
So what is this all good for? They demonstrate that for a broad range of benchmark systems involving weak bonds, the that gCP corrected method coupled with the DFT-D3 dispersion correction provides excellent results, even with B3LYP/6-31G*! This allows one to potentially run a computation on very large systems, like proteins, where large basis sets, like TZP or QZP, would be impossible. In a follow-up paper,2 they show that the B3LYP/6-31G*-gCP-D3 computations of a few Diels-Alder reactions and computations of strain energies of fullerenes match up very well with computations performed at significantly higher levels.
Once this gCP method and the D3 correction are fully integrated within popular QM programs, this combined methodology should get some serious attention. Even in the absence of this integration, these energy corrections can be obtained using the web service provided by Grimme at http://www.thch.uni-bonn.de/tc/gcpd3.
References
(1) Kruse, H.; Grimme, S. "A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems," J. Chem. Phys 2012, 136, 154101-154116, DOI: 10.1063/1.3700154
(2) Kruse, H.; Goerigk, L.; Grimme, S. "Why the Standard B3LYP/6-31G* Model Chemistry Should Not Be Used in DFT Calculations of Molecular Thermochemistry: Understanding and Correcting the Problem," J. Org. Chem. 2012, 77, 10824-10834, DOI: 10.1021/jo302156p