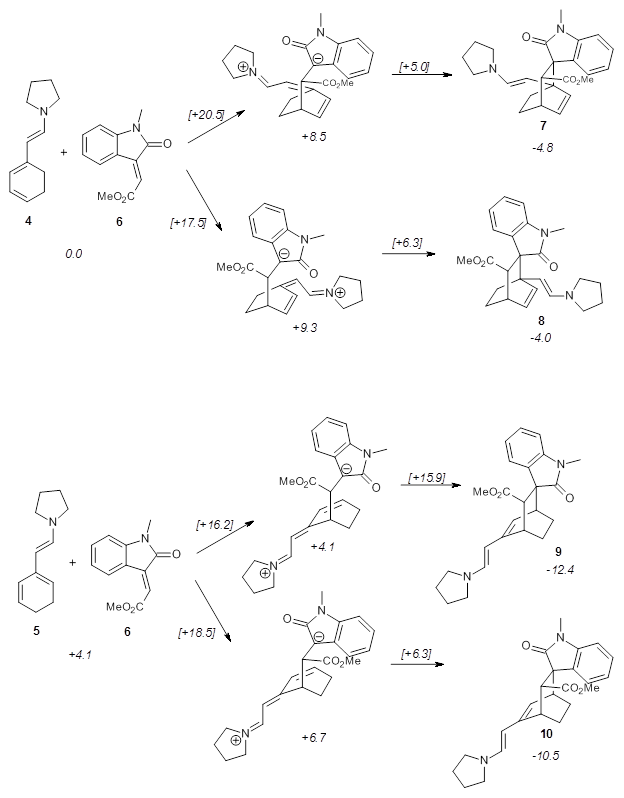
A note here on a few recent Angew. Chem. articles of interest to readers of this blog. The first is a comment by Frenking¹ concerning the “trilogue” by Shaik, Hoffmann and Rzepa² which discusses the nature of C₂, especially the notion that this molecules may possess a quadruple bond (see this post for a previous post on this article.) Frenking argues that the force constant associated with the C-C stretch in C₂ is smaller than that in acetylene, so how can one argue that there is some quadruple bond character in C₂? A reply from the original authors³ accompanies the comment by Frenking, and they respond by noting that the PES for bond stretching is unusually flat. I had the generally sense, though, that the authors of both articles were really talking past each other and that an opportunity for a more fruitful discussion has been missed.

The other article of note is an excellent review of de novo enzyme design as performed by the Baker and Houk labs.⁴ This review, authored by leaders of this effort, highlights their approach to this “holy grail” problem. The general notion is to use standard tools of computational chemistry to design a theozyme. Next, this theozyme is placed into known protein motifs with the attempt to have it fit without too much steric clash. The protein is then mutated one residue at a time to optimize the fit and binding of the theozyme to substrate. Lastly, the best targets are synthesized and tested. (The reader can see my post one of their projects: synthetic Diels-Alderase.)

References

(1) Frenking, G.; Hermann, M. "Critical Comments on “One Molecule, Two Atoms, Three
Views, Four Bonds?”," Angew. Chem. Int. Ed. 2013, 52, 5922-5925. DOI: 10.1002/anie.201301485.

(2) Shaik, S.; Rzepa, H. S.; Hoffmann, R. "One Molecule, Two Atoms, Three Views, Four
Bonds?," Angew. Chem. Int. Ed. 2013, 52, 3020-3033, DOI: 10.1002/anie.201208206.

(3) Danovich, D.; Shaik, S.; Rzepa, H. S.; Hoffmann, R. "A Response to the Critical Comments on “One Molecule, Two Atoms, Three Views, Four Bonds?”," Angew. Chem. Int. Ed. 2013, 52, 5926-5928, DOI: 10.1002/anie.201302350.

(4) Kiss, G.; Çelebi-Ölçüm, N.; Moretti, R.; Baker, D.; Houk, K. N. "Computational Enzyme Design," Angew. Chem. Int. Ed. 2013, 52, 5700-5725, DOI: 10.1002/anie.201204077.

After much delay, the second edition of my book Computational Organic Chemistry has been sent off to the publisher! This edition is an update from the first, including many new examples of the major themes covered in the first edition. In addition there are some entirely new sections and chapters, extending the scope of the book into areas not mentioned in the first edition. There are also some new interviews of major players in the field. Comments from this blog where helpful in guiding my choices for what new materials to include in the book.

I suspect that editing of the book and making it all ready for print will take through the rest of the year. Later on this year I will discuss in the blog the new features of the book in some detail.

I intend to continue to blog on new papers through the publication of the second edition and beyond. So continue to monitor this blog for new papers and for information on where and when to purchase the second edition!

The gold standard in quantum chemistry is the method that is considered to be the best, the one that gives accurate reproduction of experimental results. The CCSD(T) method is often referred to as the gold standard, especially when a complete basis set (CBS) extrapolation is utilized. But is this method truly accurate, or simply the highest level method that is within our reach today?

Řezáč and Hobza¹ address the question of the accuracy of CCSD(T)/CBS by examining 24 small systems that exhibit weak interactions, including hydrogen bonding (e.g. in the water dimer and the water^…ammonia complex), dispersion (e.g. in the methane dimer and the methane^…ethane complex) and π-stacking (e.g. as in the stacked ethene and ethyne dimers). Since weak interactions result from quantum mechanical effects, these are a sensitive probe of computational rigor.

A CCSD(T)/CBS computation, a gold standard computation, still entails a number of approximations. These approximations include (a) an incomplete basis set dealt with by an arbitrary extrapolation procedure; (b) neglect of higher order correlations, such as complete inclusion of triples and omission of quadruples, quintuples, etc.; (c) usually the core electrons are frozen and not correlated with each other nor with the valence electrons; and (d) omission of relativistic effects. Do these omissions/approximations matter?

Comparisons with calculations that go beyond CCSD(T)/CBS to test these assumptions were made for the test set. Inclusion of the core electrons within the correlation computation increases the non-covalent bond, but the average omission is about 0.6% of the binding energy. The relativistic effect is even smaller, leaving it off for these systems involving only first and second row elements gives an average error of 0.1%. Comparison of the binding energy at CCSD(T)/CBS with those computed at CCSDT(Q)/6-311G** shows an average error of 0.9% for not including higher order configuration corrections. The largest error is for the formaldehyde dimer (the complex with the largest biding energy of 4.56 kcal mol^-1) is only 0.08 kcal mol^-1. If all three of these corrections are combined, the average error is 1.5%. It is safe to say that the current gold standard appears to be quite acceptable for predicting binding energy in small non-covalent complexes. This certainly gives much support to our notion of CCSD(T)/CBS as the universal gold standard.

An unfortunate note: the authors state that the data associated with these 24 compounds (the so-called A24 dataset) is available on their web site (www.begdb.com), but I could not find it there. Any help?

References

(1) Řezáč, J.; Hobza, P. "Describing Noncovalent Interactions beyond the Common Approximations: How Accurate Is the “Gold Standard,” CCSD(T) at the Complete Basis Set Limit?," J. Chem. Theor. Comput., 2013, 9, 2151–2155, DOI: 10.1021/ct400057w.

Computing the optical rotation of simple organic molecules can be a real challenge. One of the classic problems is methyloxirane. DFT typically gets the wrong sign, let alone the wrong value. Cappelli and Barone¹ have developed a QM/MM procedure where methyloxirane is treated with DFT (B3LYP/aug-cc-pVDZ or CAM-B3LYP/aubg-cc-pVDZ). Then 2000 arrangements of water about methyloxirane were obtained from an MD simulation. For each of these configurations, a supermolecule containing methyloxirane and all water molecules with 16 Å was identified. The waters of the supermolecule were treated as a polarized force field. This supermolecule is embedded into bulk water employing a conductor-polarizable continuum model (C-PCM). Lastly, inclusion of vibrational effects, and averaging over the 2000 configurations, gives a predicted optical rotation at 589 nm that is of the correct sign (which is not accomplished with a gas phase or simple PCM computation) and is within 10% of the correct value. The full experimental ORD spectrum is also quite nicely matched using this theoretical approach.

References

(1) Lipparini, F.; Egidi, F.; Cappelli, C.; Barone, V. "The Optical Rotation of Methyloxirane in Aqueous Solution: A Never Ending Story?," J. Chem. Theor. Comput. 2013, 9, 1880-1884, DOI: 10.1021/ct400061z.

InChIs

(R)-Methyloxirane:
InChI=1S/C3H6O/c1-3-2-4-3/h3H,2H2,1H3/t3-/m1/s1
InChIKey=GOOHAUXETOMSMM-GSVOUGTGSA-N

I was intending to write a post regarding an interesting paper on o-phenylene polymers. This paper describes experiments and computations on the hexamer, with particular attention paid to arene-arene interactions.¹ These compounds fold into a helix, which has obvious application to many biological systems (DNA and the α-helix of peptides).

One of the things I am attempting to convey in this blog is the advantage of electronic communication in the sciences. In particular, I incorporate 3-dimensional structures of molecules in a way that allows the reader to interact with the molecule through a Java applet. (If you haven’t done this yet, any of the 3-D static images in this blog are actually linked to active structures – simply click on them and allow the Java applet to load.)

Now the paper by Hartley and co-workers does include supporting information with the coordinates of the different conformers of the o-phenylene hexamer, and I was all set to create images and incorporate the active molecules within a post. However, the pdf version of the supporting materials, while looking fine when viewed, actually has destroyed the data. I cannot copy-and-paste the coordinates into any program – the coordinates are completely corrupted! This is yet another example of how pdf is perhaps one of the worst choices for data deposition, as Peter Murray-Rust has often noted in his blog.

So until the supporting materials are fixed in some way, I will not, really can not, write up a post on it. Authors please remember to submit useful supporting materials!

References

(1) Mathew, S. M.; Engle, J. T.; Ziegler, C. J.; Hartley, C. S. "The Role of Arene–Arene Interactions in the Folding of ortho-Phenylenes," J. Am. Chem. Soc. 2013, 135, 6714-6722, DOI: 10.1021/ja4026006.

Alonso and coworkers have again (see this post employed laser-ablation molecular-beam Fourier-transform microwave (LA-MB-MW)spectroscopy to discern the gas phase structure of an important biological compound: cytosine.¹ They identified five tautomers of cytosine 1-5. Comparison between the experimental and computational (MP2/6-311++G(d,p) microwave rotational constants and nitrogen nuclear quadrupole coupling constants led to the complete assignment of the spectra. The experimental and calculated rotational constants are listed in Table 1.

Table 1. Rotational constants (MHz) for 1-5.

The experimental and computed relative free energies are listed in Table 2. There is both not a complete match of the relative energetic ordering of the tautomers, nor is there good agreement in their magnitude. Previous computations² at CCSD(T)/cc-pVQZ//CCSD//cc-pVTZ are in somewhat better agreement with the gas-phase experiments.

Table 2. Relative free energies (kcal mol^-1) of 1-5.

References

(1) Alonso, J. L.; Vaquero, V.; Peña, I.; López, J. C.; Mata, S.; Caminati, W. "All Five Forms of Cytosine Revealed in the Gas Phase," Angew. Chem. Int. Ed. 2013, 52, 2331-2334, DOI: 10.1002/anie.201207744.

(2) Bazso, G.; Tarczay, G.; Fogarasi, G.; Szalay, P. G. "Tautomers of cytosine and their excited electronic states: a matrix isolation spectroscopic and quantum chemical study," Phys. Chem. Chem. Phys., 2011, 13, 6799-6807, DOI:10.1039/C0CP02354J.

InChIs

cytosine: InChI=1S/C4H5N3O/c5-3-1-2-6-4(8)7-3/h1-2H,(H3,5,6,7,8)
InChIKey=OPTASPLRGRRNAP-UHFFFAOYSA-N

Conformational analysis is one of the tasks that computation chemistry is typically quite adept at and computational chemistry is frequently employed for this purpose. Thus, benchmarking methods for their ability to predict accurate conformation energies is quite important. Martin has done this for alkanes¹ (see this post), and now he has looked at a molecule that contains weak intramolecular hydrogen bonds. He examined 52 conformations of melatonin 1.² The structures of the two lowest energy conformations are shown in Figure 1.

1

1a

1b

Figure 1. Structures of the two lowest energy conformers of 1 at SCS-MP2/cc-pVTZ.

The benchmark (i.e. accurate) relative energies of these conformers were obtained at MP2-F12/cc-pVTZ-F12 with a correction for the role of triples: (ECCSD(T)/cc-pVTZ)-E(MP2/cc-pVTZ)). The energies of the conformers were computed with a broad variety of basis sets and quantum methodologies. The root mean square deviation from the benchmark energies is used as a measure of the utility of these alternate methodologies. Of particular note is that HF predicts the wrong ordering of the two lowest energy isomers, as do some DFT methods that use small basis sets and do not incorporate dispersion.

In fact, other than the M06 family or double hybrid functionals, all of the functionals examined here (PBE. BLYP, PBE0, B3LYP, TPSS0 and TPSS) have RMSD values greater than 1 kcal mol^-1. However, inclusion of a dispersion correction, Grimme’s D2 or D3 variety or the Vydrov-van Voorhis (VV10) non-local correction (see this post for a review of dispersion corrections), reduces the error substantially. Among the best performing functionals are B2GP-PLYP-D3, TPSS0-D3, DSD-BLYP and M06-2x. They also find the MP2.5 method to be a practical ab initio alternative. One decidedly unfortunate result is that large basis sets are needed; DZ basis sets are simply unacceptable, and truly accurate performance requires a QZ basis set.

References

(1) Gruzman, D.; Karton, A.; Martin, J. M. L. "Performance of Ab Initio and Density Functional Methods for Conformational Equilibria of CnH2n+2 Alkane Isomers (n = 4-8)," J. Phys. Chem. A 2009, 113, 11974–11983, DOI: 10.1021/jp903640h.

(2) Fogueri, U. R.; Kozuch, S.; Karton, A.; Martin, J. M. L. "The Melatonin Conformer Space: Benchmark and Assessment of Wave Function and DFT Methods for a Paradigmatic Biological and
Pharmacological Molecule," J. Phys. Chem. A 2013, 117, 2269-2277, DOI: 10.1021/jp312644t.

InChIs

1: InChI=1S/C13H16N2O2/c1-9(16)14-6-5-10-8-15-13-4-3-11(17-2)7-12(10)13/h3-4,7-8,15H,5-6H2,1-2H3,(H,14,16)
InChIKey=DRLFMBDRBRZALE-UHFFFAOYSA-N

Halskov, et al.¹ reported the interesting Diels-Alder selectivity shown in Scheme 1. The linear trienamine 1 did not undergo the Diels-Alder addition, while the less stable cross-conjugated diene 2 does react with 3 with high diastereo- and enantioselectivity. Their MPW1K/6-31+G(d,p) computations on a model system, carried out for a gas-phase environment, indicated a concerted mechanism, with thermodynamic control. However, the barrier for the reverse reaction for the kinetic product was computed to be greater than 30 kcal mol^-1, casting doubt on the possibility of thermodynamic control.

Scheme 1.

Houk and co-workers² have re-examined this reaction with the critical addition of performing the computation including the solvent effects. Since the stepwise alternatives involve the formation of zwitterions, solvent can be critical in stabilizing these charge-separated species, intermediates that might be unstable in the gas phase. Henry Rzepa has pointed out in his blog and on many comments in this blog about the need to include solvent, and this case is a prime example of the problems inherent in neglecting solvation.

Using models of the above reaction Houk located two zwitterionic intermediates of the Michael addition for both the reactions of 4 with 6 and of 5 with 6. The second step then involves the closure of the ring to give what would be Diels-Alder products. This is shown in Scheme 2. They were unable to locate transition states for any concerted pathways. The computations were done at M06-2x/def2-TZVPP/IEFPCM//B97D/6-31+G(d,p)/IEFPCM, modeling trichloromethane as the solvent.

Scheme 2. Numbers in italics are energies relative to 4 + 6.

The activation barrier for the second step in each reaction is very small, typically less than 5 kcal mol^-1, so the first step is rate determining. The lowest barrier is for the reaction of 5 leading to 9, analogous to the observed product. Furthermore, 9 is also the thermodynamic product. Thus, the regioselectivity is both kinetically and thermodynamically controlled through a stepwise reaction. This conclusion is only possible by including solvent in order to stabilize the zwitterionic intermediates, and should be a word of caution for everyone doing computations: be sure to include solvent for any reactions that involved charged or charge-separated species at any point along the reaction pathway!

References

(1) Halskov, K. S.; Johansen, T. K.; Davis, R. L.; Steurer, M.; Jensen, F.; Jørgensen, K. A. "Cross-trienamines in Asymmetric Organocatalysis," J. Am. Chem. Soc. 2012, 134, 12943-12946,
DOI: 10.1021/ja3068269.

(2) Dieckmann, A.; Breugst, M.; Houk, K. N. "Zwitterions and Unobserved Intermediates in Organocatalytic Diels–Alder Reactions of Linear and Cross-Conjugated Trienamines," J. Am. Chem. Soc. 2013, 135, 3237-3242, DOI: 10.1021/ja312043g.

Vibrational frequencies are routinely computed within most QM codes assuming the harmonic approximation. To correct for the neglect of higher order terms (anharmonicity), along with correcting for the inherent approximations of whatever quantum mechanical method is used, the harmonic frequencies are typically corrected by using a multiplicative scaling factor. The values of the scaling factor is method-dependent: a different scaling factor is need for every method and basis set combination! Nonetheless, this is a simple approach to computing often quite reasonable vibrational frequencies.

Anharmonic corrections can also be computed, and this is usually done using perturbation theory, which requires computing the third and often fourth derivatives, a mightily expensive proposition for reasonably large molecules even with DFT, let alone with some wavefunction-based post-HF method.

Jacobsen and co-workers¹ examined a set of 176 molecules that include 2738 vibrational modes, using HF, MP2, B3LYP and PBE0 with the 6-31G(d) or 6-31+G(d,p) basis sets. The unscaled anharmonic frequencies are much better than the unscaled harmonic frequencies; for example, using B3LYP/6-31+G(d), the root mean square deviation (RMSD) for the harmonic frequencies is 78 cm^-1 and 36 cm^-1 for the anharmonic frequencies. But the scaled harmonic frequencies are just as good as the scaled anharmonic frequencies; using the same QM method, the RMSD for the scaled harmonic frequencies is 38 cm^-1 and 36 cm^-1 for the scaled anharmonic frequencies.

These authors suggest that accurate anharmonic corrections require very accurate potential energy surfaces, and so they recommend that unless you are using a very highly accurate computational model, there is no point in computing anharmonic frequencies; scaled harmonic frequencies will suffice!

References

(1) Jacobsen, R. L.; Johnson, R. D.; Irikura, K. K.; Kacker, R. N. "Anharmonic Vibrational Frequency Calculations Are Not Worthwhile for Small Basis Sets," J. Chem. Theor. Comput. 2013, 9, 951-954, DOI: 10.1021/ct300293a.

Sugars comprise a very important class of organic compounds for a variety of reasons, including dietary needs. On the chemical side, their stereochemical variations give rise to interesting
conformational questions. While sugar structures are a well-studied dating back to Fischer, most of these studies are in the solid or solution phase, and these phases can certainly play a role in dictating conformational preferences. This is seen in the differences in conformational distribution with different solvents. Only recently has instrumentation been developed (see these posts for some earlier applications: A, B, C) that can provide structural information of sugars in the gas phase. Cocinero and co-workers describe just such an analysis of fructose.¹

Using a combination of laser ablation Fourier transform microwave spectroscopy and quantum chemical computations, they have examined the gas-phase structure of this ketose. There are
quite a number of important conformational and configurational isomers to consider, as shown in Scheme 1. Fructose can exist in a pyranose form (6-member ring) with the anomeric carbon being α or β. An alternative cyclic form is the 5-member ring furanose form, which again has the two options at the anomeric position. Both the 5- and 6-member rings can ring flip, giving rise to 4 pyranose and 4 furanose forms. Of course there is also the
acyclic form.

Scheme 1. Major Frucotse isomers

The observed microwave spectrum is quite simple, showing evidence of only a single isomer. In comparing the microwave rotational constants and the quartic centrifugal distortion constants with those obtained from MP2 and M06-2x computations, it is clear that the only observed isomer is the β-pyranose isomer in its ²C₅ conformation.

Both MP2 and M06-2x (with a variety of TZ basis sets) predict this isomer to be the lowest energy form by about 2.5 kcal mol^-1. This structure is shown in Figure 1. Interestingly, B3LYP predicts the open chain configuration as the most stable isomer, with the β-pyranose isomer about 0.5 kcal mol^-1 higher in energy. The authors strongly caution against using B3LYP for any sugars.

Figure 1. MP2/maug-cc-pVTZ optimized structure of β-fructopyranose.

This most stable furanose isomer displays five intramolecular hydrogen bonds that account for its stability over all other possibilities. However, the pyranose form of fructose is very rare in nature, and the Protein Data Bank has only four examples. The furanose form is by far the more commonly found isomer (as in sucrose). Clearly, hydrogen bonding to solvent and other solvent interactions alter the conformational distribution.

References

(1) Cocinero, E. J.; Lesarri, A.; Ecija, P.; Cimas, A.; Davis, B. G.; Basterretxea, F. J.; Fernandez, J. A.; Castano, F. "Free Fructose is Conformationally Locked," J. Am. Chem. Soc. 2013, 135, 2845-2852, DOI: 10.1021/ja312393m.

InChIs:

β-fructopyranose:
InChI=1S/C5H10O6/c6-2-1-11-5(9,10)4(8)3(2)7/h2-4,6-10H,1H2
InChIKey=FFDHYUUPNCCTDA-UHFFFAOYSA-N