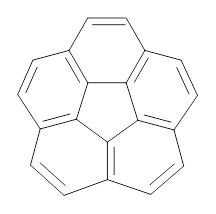
How should one assess the aromatic stabilization energy of non-planar compounds like corannulene 1? The standard approach might be to employ the homodesmotic reaction, like Reaction 1. The energy of this reaction is however quite different whether one chooses s-cis or s-trans butadiene: 67.5 kcal mol-1 with the former and 14.8 kcal mol-1 with the latter. Exactly how one balances the total number of cis/trans relationships is problematic, but worse still is that Reaction 1 does not remove the effect of strain and non-planarity of 1.
|
|
|
Reaction 1
15 H2C=CH-CH=CH2 + 20 H2C=C(CH3)2 → 1 + 10 H2C=CH2 + 20 H2C=CH-CH3
Dobrowolski, Ciesielski and Cyranski1 propose a series of reactions that extend the isomerization stabilization energy concept of Schleyer. References are chosen that involve fixed alternate polyenes by appending methylene groups, creating radialene-like compounds. Reaction 2 and 3 are two such reactions that attempt to remove strain and non-planarity effects along with balancing the cis/trans relationships and potential H-H clashes between the pendant methylene groups. They report an additional 18 variations, because there is no unique method for portioning these effects.
Reaction 2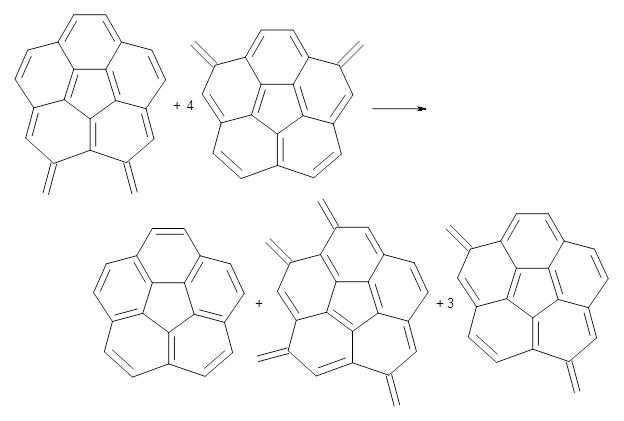
Reaction 3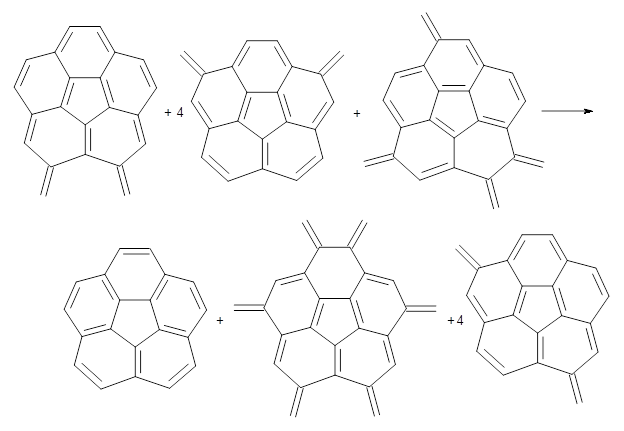
Using B3LYP/6-311G** energies with zero-point vibrational energy, the reaction energies are 46.7 and 46.3 kcal mol-1 for Reactions 2 and 3, respectively. Using all of the variations, the mean value is 44.7 kcal mol-1 with a standard deviation of only 1.2 kcal mol-1. It is clear that corranulene has a rather substantial artomatic stabilization energy, reflecting its decided aromatic character.
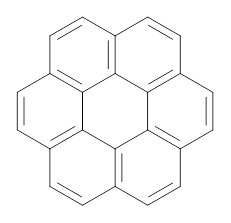
In a similar vein, they have also estimated the aromatic stabilization energy of coronene 2 as 58.4 kcal mol-1, which, while clearly demonstrating the 2 is aromatic, it does not express any “superaromaticity”.
References
(1) Dobrowolski, M. A.; Ciesielski, A.; Cyranski, M. K. "On the aromatic stabilization of corannulene and coronene," Phys. Chem. Chem. Phys., 2011, 13, 20557-20563, DOI: 10.1039/C1CP21994D
InChIs
1: InChI=1S/C21H14/c1-3-13-6-7-15-10-11-16-9-8-14-5-4-12(2)17-18(13)20(15)21(16)19(14)17/h3-11H,1H2,2H3
InChIKey=ZJQHTVPYWDRMLD-UHFFFAOYSA-N
2: InChI=1S/C24H12/c1-2-14-5-6-16-9-11-18-12-10-17-8-7-15-4-3-13(1)19-20(14)22(16)24(18)23(17)21(15)19/h1-12H
InChIKey=VPUGDVKSAQVFFS-UHFFFAOYSA-N

Ilie Fishtik responded on 24 May 2012 at 4:09 pm #
The reference state postulated by Dobrowolski, Ciesielski and Cyranski (DCC) and used to evaluate the aromatic stabilization energy (ASE) of corannulene and coronene is certainly interesting and legitimate. From a methodological point of view, however, the approach used by DCC to evaluate the ASE is wrong.
First, the reaction schemes generated by DCC are stoichiometrically arbitrary. As a result, their ASE is also arbitrary. For simplicity, let us denote the nine reference species used by DCC to evaluate the ASE of corannulene by B1, B2,…,B9 while corannulene itself is denoted by B10. Thus, two of the reactions used by DCC may be presented as
-4B2 + 2B3 – B4 + B5 + B8 + B10 = 0 -45.00 kcal/mol (8)
-4B2 + 2B3 + B9 + B10 = 0 -43.41 kcal/mol (14)
Apparently, the 18 reactions used by DCC give quite consistent ASE for corannulene. These reactions, however, can be linearly combined in an infinite number of ways, thus, generating new reactions, respectively, “new” values of ASE. For example, employing the reaction
-2B3 – 4B5 + 5B9 + B10 = 0 -37.90 kcal/mol
we have an ASE equal to -37.90 kcal/mol while using the reaction
-2B3 + 16B5 – 15B6 + B10 = 0 -66.57 kcal/mol
we obtain an ASE equal to – 66.57 kcal/mol! Notice, both of these reactions were generated by linearly combining the 18 reactions used by DCC. Clearly, including one of these “new” reactions into the “averaging” procedure will significantly modify the ASE.
The second and, decisive issue, is concerned with the very essence of the energetic/ thermodynamic measure of aromaticity. From a thermodynamic point of view aromaticity is a relative stability problem that is uniquely determined by three factors, namely, reference state, group additivity (GA) model and energetic characteristics of the species. Once these three factors are fixed there should be one and only one value of aromaticity. The massive amount of the energetic measures of aromaticity comes from the false postulate that there exist conceptually different energetic definitions of aromaticity, such as, Huckel resonance energy (RE), Dewar RE, Hess-Schaad RE, experimental or empirical RE, isodesmic and homodesmotic stabilization energies, etc. Moreover, it is erroneously stated that “Nowadays the isodesmic and especially the homodesmotic approaches are widely considered to be the most sophisticated methods for estimating the extra stability due to cyclic π-electron delocalization” (M. K. Cyranski, Chem. Rev., 2005, 105, 3773–3811). Such a viewpoint is conceptually wrong and represents the major cause of the mess we currently have in the literature when it comes to energetic evaluation of aromaticity. I’m not in a position to state who was the first to define the resonance energy (RE) as
RE = E – E(GA) (1)
where E is an energetic characteristic of the species such as HMO π-electron energy, ab initio or DFT total enthalpy or experimental enthalpy of formation while E(GA) is the same quantity calculated via a GA model. Nevertheless, whoever was the first and whatever was the reasoning to define the RE according to eq (1), it is the only thermodynamically rigorous definition of RE. Respectively, it is the only energetic or thermodynamic measure of aromaticity. All other “methods” or “approaches” are particular (and, usually, much worse) cases of eq (1). Recently (I. Fishtik, J. Phys. Chem. A 2012, 116, 1854−1863), it has been proved that eq (1) may be uniquely partitioned into contributions associated with certain types of reactions schemes. This new finding unequivocally reveals that the RE evaluated via eq (1) and the ASE evaluated via reaction schemes should coincide! The reaction schemes, however, must be generated in a game changing way.
Computational Organic Chemistry » Bowls derived from C70 responded on 06 Feb 2013 at 5:40 pm #
[…] have discussed a few bowl-shaped aromatics in this blog (see for example this and this). Kuo and Wu now report on a few bowls derived from C70-fullerenes.1 The bowl 1 was synthesized […]