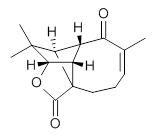
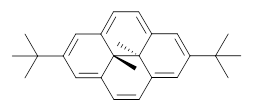
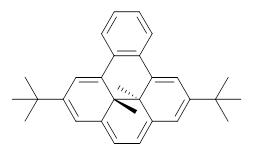
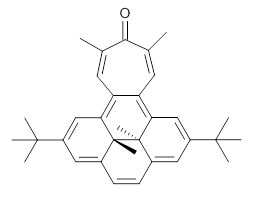
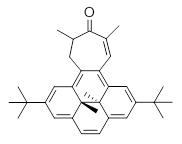
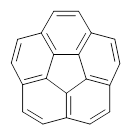
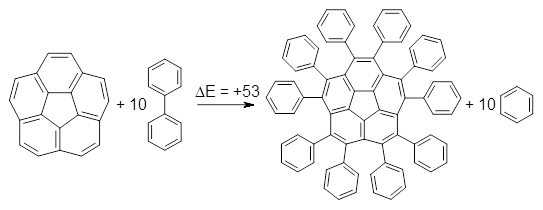
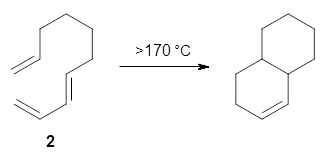
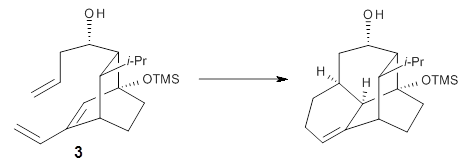
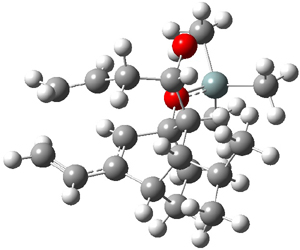
What is the appropriate basis set to use for computing optical rotations? Hedgård, Jensen, and Kongsted examined the optical rotation of 1-6 using B3LYP and CAM-B3LYP at two different wavelengths.¹ They examined a series of different basis sets, including the aug-pCS sets² (developed for NMR computations), the aug-cc-pVXZ series and 6-311++G(3df,3pd). They compared the computed optical rotation with the different basis sets with the value obtained from an extrapolated basis set computation. The mean absolute deviation using either B3LYP or CAM-B3LYP at the two different basis sets are listed in Table 1. The bottom line is that aug-pcS-2 is the preferred method, but this basis set is rather large and computations of big molecules will be difficult. The aug-pcS-1 set is the best choice for large molecules. Errors with the extensive Pople basis set and the aug-cc-pVXZ sets are quite sizable and of concern (especially at the shorter wavelength). It should also be mentioned that even with the largest aug-pcS basis sets extrapolated to the CBS limit, the computed value of the optical rotation of 3 has the wrong sign! Clearly, basis set choice is not the only issue of concern. We remain in need of a robust methodology for computing optical activity.

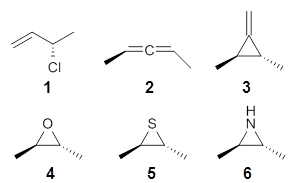
Table 1. Mean absolute deviation of the optical activities of 1-6 evaluated at two wavelengths.

References

(1) Hedegård, E. D.; Jensen, F.; Kongsted, J. "Basis Set Recommendations for DFT Calculations of Gas-Phase Optical Rotation at Different Wavelengths," J. Chem. Theory Comput. 2012, 8, 4425-4433, DOI: 10.1021/ct300359s

(2) Jensen, F. "Basis Set Convergence of Nuclear Magnetic Shielding Constants Calculated by Density Functional Methods," J. Chem. Theory Comput. 2008, 4, 719-727, DOI: 10.1021/ct800013z

The natural product aquatolide has the proposed structure 1.¹ Before starting to investigate this rather unusual structure – the 2[ladderane] component is rare and likely to be a synthetic challenge – Shaw and Tantillo opted to reassure themselves that the structure is correct.² They computed the chemical shifts of this structure at mPW1PW91/6-311+G(2d,p)//B3LYP/6-31+G(d,p) including PCM to model chloroform. Surprisingly, the mean absolute deviation of the computed ¹³C NMR shifts of 1 with the experimental values is 7.23 ppm, with the largest deviation of 24.3 ppm. The largest deviation between 1 and the experimental ¹H NMR shifts is 1.31 ppm. These large errors suggested that the structure is wrong. Surveying some 60 different possible alternative structures, largely based on other related compounds found in the same plant, they landed on 2. Here the mean absolute deviation of the computed ¹³C chemical shifts is only 1.37 ppm, with a maximum deviation of only 4.3 ppm. Similar dramatic improvement is also seen with the proton chemical shifts. Excellent agreement is also seen in the computed ¹H-¹H coupling constants between those computed for 2 and the experimental spectrum. Crystallization of aquatolide and subsequent determination of the structure using x-ray diffraction confirms that the actual structure of aquatolide is 2.

References

(1) San Feliciano, A.; Medarde, M.; Miguel del Corral, J. M.; Aramburu, A.; Gordaliza, M.; Barrero, A. F. "Aquatolide. A new type of humulane-related sesquiterpene lactone," Tetrahedron Lett. 1989, 30, 2851-2854, DOI: 10.1016/s0040-4039(00)99142-1

(2) Lodewyk, M. W.; Soldi, C.; Jones, P. B.; Olmstead, M. M.; Rita, J.; Shaw, J. T.; Tantillo, D. J. "The Correct Structure of Aquatolide—Experimental Validation of a Theoretically-Predicted Structural Revision," J. Am. Chem. Soc. 2012, DOI: 10.1021/ja3089394

InChIs

1: InChI=1S/C15H18O3/c1-7-5-4-6-15-9(11(7)16)8-10(15)12(14(8,2)3)18-13(15)17/h5,8-10,12H,4,6H2,1-3H3/t8-,9+,10+,12+,15+/m1/s1
InChIKey=JGSDEQLPLHCECO-NIDGLEHPSA-N

2: InChI=1S/C15H18O3/c1-7-5-4-6-15-9-8(10(7)16)11(15)14(2,3)12(9)18-13(15)17/h5,8-9,11-12H,4,6H2,1-3H3/b7-5-/t8-,9-,11+,12-,15+/m0/s1
InChIKey=OKZHLNWYFSWUMD-AETBLWMGSA-N

A comprehensive evaluation of how different computational methods perform in predicting the energies of monosaccharides comes to some very interesting conclusions. Sameera and Pantazis¹ have examined the eight different aldohexoses (allose, alltrose, glucose, mannose, gulose, idose, galactose and talose), specifically looking at different rotomers of the hydroxymethyl group, α- vs. β-anomers, pyranose vs. furanose isomers, ring conformations (¹C₄ vs skew boat forms), and ring vs. open chain isomers. In total, 58 different structures were examined. The benchmark computations are CCSD(T)/CBS single point energies using the SCS-MP2/def2-TZVPP optimized geometries. The RMS deviation from these benchmark energies for some of the many different methods examined are listed in Table 1.

Table 1. Average RMS errors (kJ mol^-1) of the 58 different monosaccharide structures for
different computational methods.

Perhaps the most interesting take-home message is that CEPA, MP2, the double hybrid methods and M06-2x all do a very good job at evaluating the energies of the carbohydrates. Given the significant computational advantage of M06-2x over these other methods, this seems to be the functional of choice! The poorer performance of the DFT methods over the ab initio methods is primarily in the relative energies of the open-chain isomers, where errors can be on the order of 10-20 kJ mol^-1 with most of the functionals; even the best overall methods (M06-2x and the double hybrids) have errors in the relative energies of the open-chain isomers of 7 kJ mol^-1. This might be an area of further functional development to probe better treatment of the open-chain aldehydes vs. the ring hemiacetals.

References

(1) Sameera, W. M. C.; Pantazis, D. A. "A Hierarchy of Methods for the Energetically Accurate Modeling of Isomerism in Monosaccharides," J. Chem. Theory Comput. 2012, 8, 2630-2645, DOI:10.1021/ct3002305

I have long been a proponent of the Internet as holding the potential for revolutionizing how chemists communicate. This blog represents one of the ways that electronic communication can enhance how we exchange ideas.

This blog began as a means for me to maintain the currency of my book Computational Organic Chemistry. I realized that as soon as the book was physically printed and distributed, it was already 6 months out of date, and every subsequent day the book became that much less current. But the blog provides a mechanism for me to continuously provide updates to the book. As new articles are published, I can comment on them with the same perspective as I brought to the book.

I have been blogging now for over 5 years: almost 300 posts discussing well over 300 new articles relevant to computational organic chemistry. While the number of comments and commenters has not been particularly large, many of these comments are quite astute and there has been the occasional quite interesting back-and-forth discussion.

While my blogging is not entirely altruistically motivated, this has been more of a labor of love than anything else. So one might understand my dismay when about two weeks ago I received email messages from Jan and Henry and Eugene telling me that when they tried to access the blog, their browsers came back with a malware notice message from Google. Apparently Google will scan sites for problems and most current browsers will poll Google for the health of these sites prior to actually connecting to them.

My blog became infected somehow, and now I had to figure out how to remove the infestation! Fortunately, my son is a CS guru and so when I visited him for the Thanksgiving weekend we set out to disinfect the wordpress installation. After a bit of poking around, we found that every css file associated with the theme had unauthorized byte-code. Once we removed all of that, we submitted the site for review by Google, but to no avail – the site was still infected. So, back to more searching and we discovered that many of the plugins were infected, as were other themes. So another round of removing the foreign code and resubmittal to Google, and finally we passed inspection. The blog is now running clean!

But what a pain! And all for some junk that simply referred people to other sites. This headache cost a number of hours of searching and cleaning and worrying – for no good reason at all. (And I had a free software consultant – Thanks D!) I must say that I came seriously close to deciding to chuck the blog entirely. The hassle of maintaining the site and fighting off spammers and the like are truly the seamy side of the web. If one ever hears the comment that distributing information on the net is “free” – remind them of the constant vigilance needed to ward off spammers and hackers and other vermin. And my little site is nowhere near as vital or subject to attack as say a bank, or a military base, or even a scientific publisher.

I appreciate more now the true cost of doing business on the web. I dismay about the future – the web is very much the “wild west” and lawlessness pervades. I worry that I (and others) may finally just give up. I wish I knew of a solution, but I realize that there is no way to perfectly secure a site.

So if anyone out there has a WordPress site and gets infected I can offer some advice for cleansing – and if anyone has advise as to how to stem the malware tide, please share!

The use of computed NMR coupling constants is starting to grow. In a previous post I discussed a general study by Rablen and Bally on methods for computing J_HH coupling constants. Now Williamson reports methods to experimentally obtain ¹ J_CC and ³J_CC coupling constants.¹ These were obtained for strychnine. He then computed the coupling constants in two steps. Using the B3LYP/6-31G(d) optimized geometry, first the Fermi contact contribution was computed at B3LYP/6-31+G(d,p) by uncontracting the basis set and adding an additional tighter set of polarization functions. Second, the remaining terms (spin-dipolar, paramagnetic spin-orbit and diamagnetic spin-orbit coupling) were computed with the 6-31+Gd,p) set without modifications. The two computed terms were added to give the final estimate.

A plot of the experimental vs. the DFT computed ¹ J_CC and ³J_CC coupling constants shows
an excellent linear relation, with correlation coefficient of 0.9986 and a slope of 0.98. The mean absolute deviation for the computed and experimental ¹ J_CC and ³J_CC coupling constants is 1.0
Hz and 0.4 Hz, respectively, both well within the experimental error.

I expect that computed NMR spectra will continue to be a growth area, especially for structural identification.

References

(1) Williamson, R. T.; Buevich, A. V.; Martin, G. E. "Experimental and Theoretical Investigation of ¹J_CC and ⁿJ_CC Coupling Constants in Strychnine," Org. Letters 2012, 14, 5098-5101, DOI: 10.1021/ol302366s

InChIs

strychnine:
InChI=1S/C21H22N2O2/c24-18-10-16-19-13-9-17-21(6-7-22(17)11-12(13)5-8-25-16)14-3-1-2-4-15(14)23(18)20(19)21/h1-5,13,16-17,19-20H,6-11H2/t13-,16-,17-,19-,20-,21+/m0/s1
InChIKey=QMGVPVSNSZLJIA-FVWCLLPLSA-N

Assessing the degree of aromaticity in a novel compound has been a much sought after prize, and is the topic of much of Chapter 2 in my book. An interesting approach is described in a recent JACS paper by Williams and Mitchell.¹ The interior methyl groups of 1 sit above and below the ring plane of the aromatic dihydropyrene and provide an interesting magnetic probe of the aromaticity; the chemical shift of these methyl groups are δ -4.06ppm, far upfield as they sit in the shielded region above the aromatic plane. Annelation of a benzene ring to give 2 should reduce the ring current, thereby reflecting a reduced aromatic character. In fact, the chemical shifts of the methyls in 2 are δ -1.58 ppm. This relatively large chemical shift difference provides a means for measuring the aromatic influence of other fused rings.

Suppose a different (non-benzene) ring were fused onto 1. Williams and Mitchell examined two such cases 3 and 4 (among others). These two compounds were prepared and studied by ¹H NMR and also by B3LYP/6-31G* computations. The optimized structures of 3 and 4 are shown in Figure 1.

The experimental chemical shifts of the interior methyl groups are δ -3.32 ppm. This downfield shift of the methyls relative to their position in 1 reflects some homoaromatic character of the cycloheptatrienyl ring. If we take the difference in the methyl chemical shifts in 1 and 2 to reflect the aromatic character of benzene (2.48 ppm), then the difference in the chemical shifts of 3 and 1 (0.74 ppm) indicates that the cycloheptatrienyl ring has 0.74/2.48*100 = 30% the (homo)aromatic character of benzene! Similarly, the methyl chemical shifts in 4 are δ -3.56 ppm, leading to an estimate of the aromatic character of the tropone ring of 20%.

3

4

Figure 1. B3LYP/6-31G* optimized geometries of 3 and 4.

In using NICS to estimate the aromatic character, they make use of the average value of the NICS in the four rings of the dihydropyrene fragment. The baseline comparison is then in the average NICS value of 1 compared to that in 5, a compound that has a similar geometry but without the aromatic character of the fused benzene ring. This difference is 11.42ppm. The analogous relationship is then 3 with 6 (a NICS difference of 3.81 ppm) and 4 with 7 (a NICS difference of 2.77ppm). This gives an estimate of the (homo)aromatic character of cycloheptatriene of 33% and the aromatic character of tropolone of 24%. This NICS estimates are in great agreement with the experimental values from the proton chemical shifts.

References

(1) Williams, R. V.; Edwards, W. D.; Zhang, P.; Berg, D. J.; Mitchell, R. H. "Experimental Verification of the Homoaromaticity of 1,3,5-Cycloheptatriene and Evaluation of the Aromaticity of Tropone and the Tropylium Cation by Use of the Dimethyldihydropyrene Probe," J. Am. Chem. Soc. 2012, 134, 16742-16752, DOI: 10.1021/ja306868r.

InChIs

1: InChI=1S/C26H32/c1-23(2,3)21-13-17-9-11-19-15-22(24(4,5)6)16-20-12-10-18(14-21)25(17,7)26(19,20)8/h9-16H,1-8H3/t25-,26-
InChIKey=SEGNSURCRWXVRS-DIVCQZSQSA-N

2: InChI=1S/C30H34/c1-27(2,3)21-15-19-13-14-20-16-22(28(4,5)6)18-26-24-12-10-9-11-23(24)25(17-21)29(19,7)30(20,26)8/h9-18H,1-8H3/t29-,30-/m1/s1
InChIKey=JQXZCWYPFGGVNF-LOYHVIPDSA-N

3: InChI=1S/C33H40/c1-20-13-21(2)15-27-26(14-20)28-18-24(30(3,4)5)16-22-11-12-23-17-25(31(6,7)8)19-29(27)33(23,10)32(22,28)9/h11-12,14-19H,13H2,1-10H3/t32-,33-/m1/s1
InChIKey=MUBRTBMPRBJVOC-CZNDPXEESA-N

4: InChI=1S/C33H38O/c1-19-13-25-26(14-20(2)29(19)34)28-18-24(31(6,7)8)16-22-12-11-21-15-23(30(3,4)5)17-27(25)32(21,9)33(22,28)10/h11-18H,1-10H3/t32-,33-/m1/s1
InChIKey=OWIRQHSHEVFPPM-CZNDPXEESA-N

I just returned from the Southwest Theoretical Chemistry Conference held at Texas A&M University. My thanks again to Steven Wheeler for the invitation to speak at the meeting and for putting together a very fine program and conference.

Among the many interesting talks was one by Sebastian Kozuch who reported on an interesting double hybrid methodology.^1,2 Working with Jan Martin, they defined a procedure that Kozuch referred to as “putting Stefan Grimme into a blender”. They extend the double hybrid concept first suggested by Grimme that adds on an MP2-like correction functional. Kozuch and Martin substitute a spin-component scaled MP2 (SCS-MP2) model for the original MP2 correction. SCS-MP2 was also proposed by Grimme. Lastly, they add on a dispersion correction, an idea championed by Grimme too. The exchange-correlation term is defined as

E_XC = c_XE_X ^DFT + (1 – c_x)E_x^HF + c_CE_C^DFT + c_OE_O^MP2 + c_SE_S^MP2 + s₆E_D

where c_X is the coefficient for the amount of DFT exchange, c_C the amount of DFT correlation, c_C and c_S the amount of opposite- and same-spin MP2, and s₆ the amount of dispersion. They name this procedure DSD-DFT for Dispersion corrected, Spin-component scaled Double hybrid DFT.

In their second paper on this subject, they propose the use of the PBEP86 functional for the DFT components.² Benchmarking against a variety of standard databases, including kinetic data, thermodynamic data, along with inorganic and weakly interacting systems, this method delivers the lowest mean error among a small set of functionals. Kozuch reported at the conference on a number of other combinations and should have a publication soon suggesting an even better method. Importantly, these DSD-DFT computations can be run with most major quantum codes including Orca, Molpro, Q-Chem and Gaussian (with a series of IOP specifications).

While double hybrid methods don’t have quite the performance capabilities of regular DFT, density fitting procedures offer the possibility of a significant reduction in computational time. These DSD-DFT methods are certainly worthy of fuller explorations.

References

(1) Kozuch, S.; Gruzman, D.; Martin, J. M. L. "DSD-BLYP: A General Purpose Double Hybrid Density Functional Including Spin Component Scaling and Dispersion Correction," J. Phys. Chem. C, 2010, 114, 20801-20808,
DOI: 10.1021/jp1070852

(2) Kozuch, S.; Martin, J. M. L. "DSD-PBEP86: in search of the best double-hybrid DFT with spin-component scaled MP2 and dispersion corrections," Phys. Chem. Chem. Phys. 2011, 13, 20104-20107, DOI: 10.1039/C1CP22592H

Corranulene 1 is a bowl-shaped aromatic compound. It inverts through a planar transition state with a barrier of at 11.5 kcal mol^-1. What changes would be found if one per-phenylated corranulene, making 2?

Scott¹ has prepared 2a-c by arylating corranulene using phenylboroxin and palladium acetate and repeating this arylation four times. Amazing to me is that the yield of 2c is 54%! The BMK/cc-pVDZ optimized structure of 2a is shown in Figure 1. One can readily see that the bowl is nearly flat (click on the image to activate Jmol; the x-ray structure of 2b has the bowl depth of only 0.248 Å, compared to a depth of 0.87 Å in 1.

Interestingly, 2 inverts through a chiral TS (shown in Figure 1) so that inversion does not create the enantiomer! The computed barrier height is only 2.5 kcal mol^-1.

2a

2aTS

Figure 1. BMK/cc-pVDZ optimized structures of 2a and the bowl inversion transition state 2aTS.

The flatter bowl results in longer bonds and wider angles about the rim of 2 than in 1. As one might expect, 2a is very strained: the BMK/cc-pVDZ estimation is that 2 is 53 kcal mol^-1 more strained than 1, using the homodesmotic Reaction 1. In total, this is a real nice study of using strain to alter shape.

References

(1) Zhang, Q.; Kawasumi, K.; Segawa, Y.; Itami, K.; Scott, L. T. "Palladium-Catalyzed C–H Activation Taken to the Limit. Flattening an Aromatic Bowl by Total Arylation," J. Am. Chem. Soc., 2012, 134, 15664-15667, DOI: 10.1021/ja306992k

InChIs

1: InChI=1S/C20H10/c1-2-12-5-6-14-9-10-15-8-7-13-4-3-11(1)16-17(12)19(14)20(15)18(13)16/h1-10H
InChIKey=VXRUJZQPKRBJKH-UHFFFAOYSA-N

2a: InChI=1S/C80H50/c1-11-31-51(32-12-1)61-62(52-33-13-2-14-34-52)72-65(55-39-19-5-20-40-55)66(56-41-21-6-22-42-56)74-69(59-47-27-9-28-48-59)70(60-49-29-10-30-50-60)75-68(58-45-25-8-26-46-58)67(57-43-23-7-24-44-57)73-64(54-37-17-4-18-38-54)63(53-35-15-3-16-36-53)71(61)76-77(72)79(74)80(75)78(73)76/h1-50H
InChIKey=OGBCICIRFDLAPN-UHFFFAOYSA-N

2b: InChI=1S/C120H130/c1-111(2,3)81-51-31-71(32-52-81)91-92(72-33-53-82(54-34-72)112(4,5)6)102-95(75-39-59-85(60-40-75)115(13,14)15)96(76-41-61-86(62-42-76)116(16,17)18)104-99(79-47-67-89(68-48-79)119(25,26)27)100(80-49-69-90(70-50-80)120(28,29)30)105-98(78-45-65-88(66-46-78)118(22,23)24)97(77-43-63-87(64-44-77)117(19,20)21)103-94(74-37-57-84(58-38-74)114(10,11)12)93(73-35-55-83(56-36-73)113(7,8)9)101(91)106-107(102)109(104)110(105)108(103)106/h31-70H,1-30H3
InChIKey=UQHBWLRORHEQNL-UHFFFAOYSA-N

2c: InChI=1S/C80H40Cl10/c81-51-21-1-41(2-22-51)61-62(42-3-23-52(82)24-4-42)72-65(45-9-29-55(85)30-10-45)66(46-11-31-56(86)32-12-46)74-69(49-17-37-59(89)38-18-49)70(50-19-39-60(90)40-20-50)75-68(48-15-35-58(88)36-16-48)67(47-13-33-57(87)34-14-47)73-64(44-7-27-54(84)28-8-44)63(43-5-25-53(83)26-6-43)71(61)76-77(72)79(74)80(75)78(73)76/h1-40H
InChIKey=MMASAVXWJRDYLD-UHFFFAOYSA-N

The intramolecular Diels-Alder reaction of 1 occurs slowly, but quantitatively, at room temperature.¹ This is unusual as most Diels-Alder cyclizations require heating to typically 200 °C. For example, the related cyclization of 2 requires heating to 170 °C.² What is the cause for this proximity-induced reaction?

Houk and Baran address this question using a computational approach.³ The Diels-Alder reaction of 2 and a simplified analogue of 1, namely 3, were computed at CPCM/M06-2x/6-311+G(d,p)//B3LYP/6-31G(d). The optimized transition states for the reaction of 2 and 3 are shown in Figure 1. The free energy of activation of 3 is 5.4 kcal mol^-1 lower in energy than the free energy of activation of 2. This is consistent with the much faster reaction of 1 than 2 observed in the experiment.

TS2

TS3

Figure 1. B3LYP/6-31G(d) for the transition states of Reactions 2 and 3.

Partitioning 3 into fragments allows Houk and Baran to apply the distortion model. They find that the rigid diene in 3 (and thereby 1) accelerates the reaction relative to the more flexible diene of 2. Further, strain relief in going from 3 (and thereby 1) to TS3 (and thereby to TS of reaction 1) and the formation of an intramolecular hydrogen bond leads to the lower activation energy of 3, and therefore of 1.

References

(1) Maimone, T. J.; Voica, A.-F.; Baran, P. S. "A Concise Approach to Vinigrol," Angew. Chem. Int. Ed. 2008, 47, 3054-3056, DOI: 10.1002/anie.200800167.

(2) Diedrich, M. K.; Klärner, F.-G.; Beno, B. R.; Houk, K. N.; Senderowitz, H.; Still, W. C. "Experimental Determination of the Activation Parameters and Stereoselectivities of the Intramolecular Diels−Alder Reactions of 1,3,8-Nonatriene, 1,3,9-Decatriene, and 1,3,10-Undecatriene and Transition State Modeling with the Monte Carlo-Jumping Between Wells/Molecular Dynamics Method," J. Am. Chem. Soc. 1997, 119, 10255-10259, DOI: 10.1021/ja9643331.

(3) Krenske, E. H.; Perry, E. W.; Jerome, S. V.; Maimone, T. J.; Baran, P. S.; Houk, K. N. "Why a Proximity-Induced Diels–Alder Reaction Is So Fast," Org. Lett. 2012, 14, 3016-3019, DOI: 10.1021/ol301083q.

InChIs

1: InChI=1S/C23H40O2Si/c1-10-12-19(24)21-20(16(3)4)18-13-14-23(21,15-17(18)11-2)25-26(8,9)22(5,6)7/h10-11,15-16,18-21,24H,1-2,12-14H2,3-9H3/t18?,19-,20?,21?,23+/m0/s1
InChIKey=NGVNTJGCNDZDEY-RHDCMTSYSA-N

2: InChI=1S/C10H16/c1-3-5-7-9-10-8-6-4-2/h3-5,7H,1-2,6,8-10H2/b7-5+
InChIKey=HXZJJSYHNPCGKW-FNORWQNLSA-N

3: InChI=1S/C20H34O2Si/c1-8-10-18(21)20(15(3)4)14-17-11-12-19(20,13-16(17)9-2)22-23(5,6)7/h8-9,13,15,17-18,21H,1-2,10-12,14H2,3-7H3/t17?,18-,19+,20?/m0/s1
InChIKey=GDQHAOHEZAJKPI-FUFFSDJGSA-N

Schreiner has expanded on his previous paper¹ regarding alkanes with very long C-C bonds, which I commented upon in this post. He and his colleagues report² now a series of additional diamond-like and adamantane-like sterically congested alkanes that are stable despite have C-C bonds that are longer that 1.7 Å (such as 1! In addition they examine the structures and rotational barriers using a variety of density functionals.

For 2, the experimental C-C distance is 1.647 Å. A variety of functionals all using the cc-pVDZ basis predict distances that are much too long: B3LYP, B96, B97D, and B3PW91. However, functionals that incorporate some dispersion, either through an explicit dispersion correction (Like B3LYP-D and B2PLYP-D) or with a functional that address mid-range or long range correlation (like M06-2x) or both (like ωB97X-D) all provide very good estimates of this distance.

On the other hand, prediction of the rotational barrier about the central C-C bond of 2 shows different functional performance. The experimental barrier, determined by ¹H and ¹³C NMR is 16.0 ± 1.3 kcal mol^-1. M06-2x, ωB97X-D and B3LYP-D, all of which predict the correct C-C distance, overestimate the barrier by 2.5 to 3.5 kcal mol^-1, outside of the error range. The functionals that do the best in getting the rotational barrier include B96, B97D and PBE1PBE and B3PW91. Experiments and computations of the rotational barriers of the other sterically congested alkanes reveals some interesting dynamics, particularly that partial rotations are possible by crossing lower barrier and interconverting some conformers, but full rotation requires passage over some very high barriers.

In the closing portion of the paper, they discuss the possibility of very long “bonds”. For example, imagine a large diamond-like fragment. Remove a hydrogen atom from an interior position, forming a radical. Bring two of these radicals together, and their computed attraction is 27 kcal mol^-1 despite a separation of the radical centers of more than 4 Å. Is this a “chemical bond”? What else might we want to call it?

A closely related chemical system was the subject of yet another paper³ by Schreiner (this time in collaboration with Grimme) on the hexaphenylethane problem. I missed this paper somehow near
the end of last year, but it is definitely worth taking a look at. (I should point out that this paper was already discussed in a post in the Computational Chemistry Highlights blog, a blog that acts as a journals overlay – and one I participate in as well.)

So, the problem that Grimme and Schreiner³ address is the following: hexaphenylethane 3 is not stable, and 4 is also not stable. The standard argument for their instabilities has been that they are simply too sterically congested about the central C-C bond. However, 5 is stable and its crystal structure has been reported. The central C-C bond length is long: 1.67 Å. But why should 5 exist? It appears to be even more crowded that either 3 or 4. TPSS/TZV(2d,2p) computations on these three compounds indicate that separation into the two radical fragments is very exoergonic. However, when the “D3” dispersion correction is included, 3 and 4 remain unstable relative to their diradical fragments, but 5 is stable by 13.7 kcal mol^-1. In fact, when the dispersion correction is left off of the t-butyl groups, 5 becomes unstable. This is a great example of a compound whose stability rests with dispersion attractions.

3: R₁ = R₂ = H
4: R₁ = tBu, R₂ = H
5: R₁ = H, R₂ = tBu

References

(1) Schreiner, P. R.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Schlecht, S.; Dahl, J. E. P.; Carlson, R. M. K.; Fokin, A. A. "Overcoming lability of extremely long alkane carbon-carbon bonds through dispersion forces," Nature 2011, 477, 308-311, DOI: 10.1038/nature10367

(2) Fokin, A. A.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Dahl, J. E. P.; Carlson, R. M. K.; Schreiner, P. R. "Stable Alkanes Containing Very Long Carbon–Carbon Bonds," J. Am. Chem. Soc., 2012, 134, 13641-13650, DOI: 10.1021/ja302258q

(3) Grimme, S.; Schreiner, P. R. "Steric Crowding Can tabilize a Labile Molecule: Solving the Hexaphenylethane Riddle," Angew. Chem. Int. Ed., 2011, 50, 12639-12642, DOI: 10.1002/anie.201103615