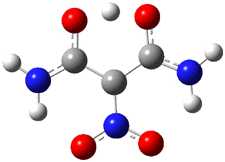
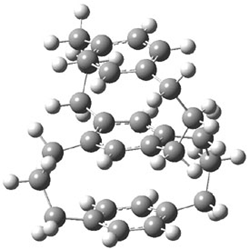
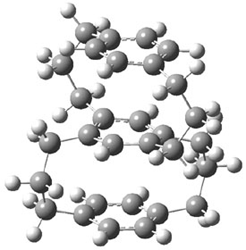
Malonaldehyde 1 possesses a very short intramolecular hydrogen bond. Its potential energy surface has two local minima (the two mirror image hydrogen-bonded structures) separated by a C_2v transition state. Schaefer reports a high-level computational study for the search for even shorter hydrogen bonds that might even lead to a single well on the PES.¹

The hydrogen bond distance is characterized by the non-bonding separation between the two oxygen atoms. Table 1 shows the O^…O distance for a number of substituted malonaldehydes computed at B3LYP/DZP++. Electron withdrawing groups on C₂ reduce the O^..O distance (see trend in 1 → 4). Electron donating groups on C₁ and C₃ also reduce this distance (see 5 and 6). Bulky substituents on the terminal carbons also reduce the O^…O distance (see 7). Combining all of these substituent effects in 8 leads to the very short O^…O distance of 2.380 Å.

Table 1. Distance (Å) between the two oxygen atoms and the barrier for hydrogen transfer of substituted malonaldehydes .¹

^aFocal point energy. ^bFocal point energy and corrected for zero-point vibrational energy.

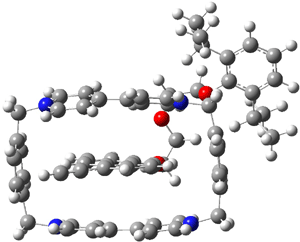
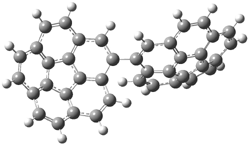
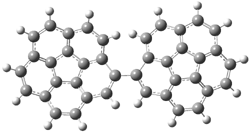
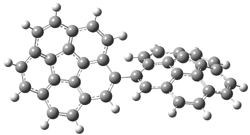
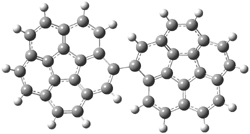
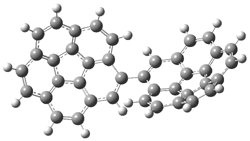
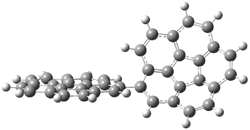
A shorter O^…O distance might imply a smaller barrier for hydrogen transfer between the two oxygens. The structures of 8 and the transition state for its hydrogen transfer are shown in Figure 1. The energies of a number of substituted malonaldehydes were computed using the focal point method, and the barriers for hydrogen transfer are listed in Table 1. There is a nice correlation between the O^…O distance and the barrier height. The barrier for 8 is quite small, suggesting that with some bulkier substituents, the barrier might vanish altogether, leaving only a symmetric structure. In fact, the barrier appears to vanish when zero-point vibrational energies are included.

8

8TS

Figure 1. B3LYP/DZP++ optimized geometries of 8 and the transition state for hydrogen transfer 8TS.¹

References

(1) Hargis, J. C.; Evangelista, F. A.; Ingels, J. B.; Schaefer, H. F., "Short Intramolecular Hydrogen Bonds: Derivatives of Malonaldehyde with Symmetrical Substituents," J. Am. Chem. Soc., 2008, 130, 17471-17478, DOI: 10.1021/ja8060672.

InChIs

1: InChI=1/C3H4O2/c4-2-1-3-5/h1-4H/b2-1-
InChIKey=GMSHJLUJOABYOM-UPHRSURJBI

2: InChI=1/C4H3NO2/c5-1-4(2-6)3-7/h2-3,6H/b4-2-
InChIKey=BHYIQMFSOGUTRT-RQOWECAXBC

3: InChI=1/C3H3NO4/c5-1-3(2-6)4(7)8/h1-2,5H/b3-1+
InChIKey=JBBHDCMVSJADCE-HNQUOIGGBS

4: InChI=1/C3H5BO2/c4-3(1-5)2-6/h1-2,5H,4H2/b3-1+
InChIKey=IQNKNZSFMBIPBI-HNQUOIGGBX

5: InChI=1/C3H6N2O2/c4-2(6)1-3(5)7/h1,6H,4H2,(H2,5,7)/b2-1-/f/h5H2
InChIKey=AOZIOAJNRYLOAH-KRHGAQEYDI

6: InChI=1/C5H8O4/c1-8-4(6)3-5(7)9-2/h3,6H,1-2H3/b4-3+
InChIKey=BYYYYPBUMVENKB-ONEGZZNKBI

7: InChI=1/C11H20O2/c1-10(2,3)8(12)7-9(13)11(4,5)6/h7,12H,1-6H3/b8-7-
InChIKey=SOZFXLUMSLXZFW-FPLPWBNLBX

8: InChI=1/C3H5N3O4/c4-2(7)1(3(5)8)6(9)10/h7H,4H2,(H2,5,8)/b2-1+/f/h5H2
InChIKey=IHYUFGCOUITNJP-CHFMFTGODK

Here’s another nice example of computed NMR spectra being
used to identify complex organic structures.¹

An alkaloid isolated from the custard apple tree was assigned the structure 1 and christened with the name samoquasine A.² Two years later, the authors determined that samoquasine A was actually identical to perlolidine 2.³ Independent synthesis of the compound with structure 1 showed that its properties were not identical to that of samoquasine A.^4,5 The properties of perlolidine were then found to differ from that of samoquasine A,⁴ leaving a void as to just what is the structure of samoquasine A.

Given that compounds 1 and the related compounds 3 and 4 had been prepared and their NMR spectra obtained, Timmons and Wipf¹ decided to compute the ¹³C NMR spectra of 48 related compounds at B3LYP/6-311+G(2d,p)//B3LYP/6-31G(d). The mean absolute difference between the computed and experimental chemical shifts for 1, 3 and 4 are less than 2 ppm. Of the remaining 45 compounds, the one whose chemical shifts match best with that of samoquasine A is 2, with a mean absolute deviation of 1.8 ppm. This agreement supports the contention that samoquasine A and perlolidine are in fact identical. The authors contend that the experimental data used to conjecture that they were not identical is in fact faulty.

References

(1) Timmons, C.; Wipf, P., "Density Functional Theory Calculation of 13C NMR Shifts of Diazaphenanthrene Alkaloids: Reinvestigation of the Structure of Samoquasine A," J. Org. Chem., 2008, 73, 9168-9170, DOI: 10.1021/jo801735e.

(2) Morita, H.; Sato, Y.; Chan, K.-L.; Choo, C.-Y.; Itokawa, H.; Takeya, K.; Kobayashi, J. i., "Samoquasine A, a Benzoquinazoline Alkaloid from the Seeds of Annona squamosa," J. Nat. Prod., 2000, 63, 1707-1708, DOI: 10.1021/np000342i.

(3) Morita, H.; Sato, Y.; Chan, K.-L.; Choo, C.-Y.; Itokawa, H.; Takeya, K.; Kobayashi, J. i., "Samoquasine A, a Benzoquinazoline Alkaloid from the Seeds of Annona squamosa," J. Nat. Prod., 2002, 65, 1748-1748, DOI: 10.1021/np0204343.

(4) Yang, Y.-L.; Chang, F.-R.; Wu, Y.-C., "Total synthesis of 3,4-dihydrobenzo[h]quinazolin-4-one
and structure elucidation of perlolidine and samoquasine A," Tetrahedron Letters, 2003, 44, 319-322, DOI: 10.1016/S0040-4039(02)02577-7.

(5) Chakrabarty, M.; Sarkara, S.; Harigaya, Y., "An Expedient Synthesis of Benzo[h]quinazolin-4(3H)-one: Structure of Samoquasine A Revisited," Synthesis, 2003, 2292-2294, DOI: 10.1055/s-2003-42409.

InChIs

1: InChI=1/C12H8N2O/c15-12-10-6-5-8-3-1-2-4-9(8)11(10)13-7-14-12/h1-7H,(H,13,14,15)/f/h14H
InChIKey=BJVYARVTSUNBMW-YHMJCDSICO

2: InChI=1/C12H8N2O/c15-12-10-7-14-11-4-2-1-3-9(11)8(10)5-6-13-12/h1-7H,(H,13,15)/f/h13H
InChIKey=ULIAUQBOGQCMQM-NDKGDYFDCS

3: InChI=1/C12H8N2O/c15-12-10-6-5-8-3-1-2-4-9(8)11(10)7-13-14-12/h1-7H,(H,14,15)/f/h14H
InChIKey=JFJSVLSRVOIBPG-YHMJCDSICJ

4: InChI=1/C12H8N2O/c15-12-11-9(7-13-14-12)6-5-8-3-1-2-4-10(8)11/h1-7H,(H,14,15)/f/h14H
InChIKey=BGYAATPHYRJYHZ-YHMJCDSICO

Here is another benchmark of the performance of DFT in handling difficult situations, in this case the interaction between nucleic acid base pairs. Sherrill¹ has examined the 124 nucleic acid base pairs from the JSCH-2005 database² compiled by Hobza and coworkers. This database includes 36 hydrogen bonded complexes, and example of which is shown in Figure 1a, and 54 stacked complex, one example of which is shown in Figure 1b.

(a)

(b)

Figure 1. Optimized geometries (RI-MP2/cc-pVTZ) of two representative structures of base pairs: (a) hydrogen bonded pair and (c) stacked pair.

The energies of these base pairs computed with four different functionals: PBE, PBE-D (where Grimme’s empirical dispersion correction³), and the recently developed MO5-2X⁴ and MO6-2X⁵ methods which attempt to treat mid-range electron correlation. The aug-cc-pVDZ basis set was used. These DFT energies are compared with the CCSD(T) energies of Hobza. The mean unsigned error (MUE) for the 28 hydrogen bonded complexes and the 54 stacked complexes are listed in Table 1.

Table 1. Mean unsigned error (kcal mol^-1) of the four DFT
methods (relative to CCSD(T)) for the hydrogen bonded and stacked base pairs.

A few interesting trends are readily apparent. First, PBE (representing standard GGA DFT methods) poorly describes the energy of the hydrogen bonded complexes, but utterly fails to treat the stacking interaction. Inclusion of the dispersion correction (PBE-D) results in excellent energies for the HB cases and quite reasonable results for the stacked pairs. Both of Truhlar’s functionals dramatically outperform PBE, though MO5-2X is probably still not appropriate for the stacked case. MO6-2X however seems to be a very reasonable functional for dealing with base pair interactions, indicating that mid-range correlation correction is sufficient to describe these complexes, and that the long-range correlation correction included in the dispersion correction, while giving improved results, is not essential.

References

(1) Hohenstein, E. G.; Chill, S. T.; Sherrill, C. D., "Assessment of the Performance of the M05-2X and M06-2X Exchange-Correlation Functionals for Noncovalent Interactions in Biomolecules," J. Chem. Theory Comput., 2008, 4, 1996-2000, DOI: 10.1021/ct800308k

(2) Jurecka, P.; Sponer, J.; Cerny, J.; P., H., "Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs," Phys. Chem. Chem. Phys., 2006, 8, 1985-1993, DOI: 10.1039/b600027d.

(3) Grimme, S., "Semiempirical GGA-type density functional constructed with a long-range dispersion correction," J. Comput. Chem., 2006, 27, 1787-1799, DOI: 10.1002/jcc.20495

(4) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., "Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions," J. Chem. Theory Comput., 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(5) Zhao, Y.; Truhlar, D. G., "The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals," Theor. Chem. Acc., 2008, 120, 215-241, DOI: 10.1007/s00214-007-0310-x.

Computed optical activity was utilized in establishing the absolute configuration of the [3,3]paracyclophane 1.¹ The helical twist of this molecule makes it chiral.

The specific rotation of (-)-1 was measured to be -123 ° [dm (g/cm³) ^-1]. Seven different conformations of R–1 were optimized, having either D₂, C₂, or C₁ symmetry, at B3LYP/TZVP. The two lowest energy conformers (at B3LYP/6-31G(d) – the authors did not supply coordinates in their supporting materials!) are shown in Figure 1.

1a (0.0)

1b (0.49)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energy (kcal mol^-1 of the two lowest energy conformers of 1.

The TDDFT computed value for [α]_D for the lowest energy conformer is -171.7 ° [dm (g/cm³)^-1]. In fact, the range of [α]_D for seven conformers is -124.4 to -221.8. These values are consistent with the experimental observation in both sign and magnitude. The computed CD spectrum of the seven R–1 conformations are similar to the experimental spectra of (-)-1. Thus, one can conclude that the two enantiomers are R-(-)-1 and S-(+)-1.

References

(1) Muranaka, A.; Shibahara, M.; Watanabe, M.; Matsumoto, T.; Shinmyozu, T.; Kobayashi, N., "Optical Resolution, Absolute Configuration, and Chiroptical Properties of Three-Layered [3.3]Paracyclophane(1)," J. Org. Chem., 2008, 73, 9125-9128, DOI: 10.1021/jo801441h

InChIs

1: InChI=1/C31H38/c1-3-7-28-22-30-12-6-10-27-20-18-26(19-21-27)9-5-11-29(28)23-31(30)13-4-8-25-16-14-24(2)15-17-25/h14-23H,3-13H2,1-2H3
InChIKey=GFTKQZANYFICNS-UHFFFAOYAN

Host-guest recognition is a major theme of modern chemistry. Computation of these systems remains a real challenge for many reasons, especially the typically large size of the molecules involved and the need for accurately computing weak, non-covalent interactions. This latter point remains a major problem with density functional theory.

Goddard has now examined a rotaxane system.¹ Goddard employed a variety of functionals (B3LYP. PBE, and MO6 variants) to 1, a compound prepared by Stoddart.² The counterion of the experimentally prepared rotoxane is PF₆^–; in the computations, Goddrad employed either no counterions or four chloride ions.

The optimized structure of 1 without counterions computed at B3LYP/6-31G** and MO6-L/6-31G** are shown in Figure 1. The major difference in these structures is the orientation of the naphthyl group inside the host. B3LYP predicts that it is skewed, while MO6-L predicts that it lies parallel to the bipyridinium side. The x-ray structure has the parallel structure, similar to that found with MO6-L, though the pendant bis-i-proylphenyl ring is farther down in the x-ray structure than in the computed structure.

(a)

(b)

Figure 1. Optimized structure of 1⁴⁺
(a) B3LYP/6-31G** and (b) MO6-L/6-31G**.¹

None of the methods perform particularly well in computing the binding energy of the host and guest. The experimental value is -4.9 ± 1 kcal mol^-1. In the gas phase, the two methods predict that the system is bound, -24.9 (B3LYP, -75.2 kcal mol^-1, MO6-L). In acetonitrile, B3LYP predicts that it is unbound, while MO6-L predicts a binding energy of -27.5 kcal mol^-1. Inclusion of four chloride ions leads to some improvement in the binding energy in the gas phase but not for the solution phase.

The excitation energy is 3.50 eV.Computation of the excitation energy is poor with B3LYP (1.33 eV) but nearly exact with MO6-HF//MO6-L (3.42 eV).

Goddard concludes that computation of these sort of interlocked molecules should be performed with the MO6 family of functionals, but clearly more work is needed if accurate energies are required.

References

(1) Benitez, D.; Tkatchouk, E.; Yoon, I.; Stoddart, J. F.; Goddard, W. A., "Experimentally-Based Recommendations of Density Functionals for Predicting Properties in Mechanically Interlocked Molecules," J. Am. Chem. Soc., 2008, 130, 14928-14929, DOI: http://dx.doi.org/10.1021/ja805953u.

(2) Nygaard, S.; Leung, K. C. F.; Aprahamian, I.; Ikeda, T.; Saha, S.; Laursen, B. W.; Kim, S.-Y.; Hansen, S. W.; Stein, P. C.; Flood, A. H.; Stoddart, J. F.; Jeppesen, J. O., "Functionally Rigid Bistable [2]Rotaxanes," J. Am. Chem. Soc., 2007, 129, 960-970, DOI: http://dx.doi.org/10.1021/ja0663529

InChIs

Guest: InChI=1/C28H32O3/c1-6-22-10-7-14-26-25(22)13-9-15-27(26)30-18-16-29-17-19-31-28-23(20(2)3)11-8-12-24(28)21(4)5/h1,7-15,20-21H,16-19H2,2-5H3
InChIKey=HYRADSXCSHFXAZ-UHFFFAOYAJ

Host: InChI=1/C36H32N4/c1-2-30-4-3-29(1)25-37-17-9-33(10-18-37)35-13-21-39(22-14-35)27-31-5-7-32(8-6-31)28-40-23-15-36(16-24-40)34-11-19-38(26-30)20-12-34/h1-24H,25-28H2/q+4
InChIKey=URORLZXVTFVIPS-UHFFFAOYAV

Concern about the use of DFT for general use in organic chemistry remains high; see my previous posts (1, 2, 3). Houk has now examined the reaction enthalpies of ten simple Diels-Alder reactions using a variety of functionals in the search for the root cause of the problem(s).¹

The ten reactions are listed in Scheme 1, and involve cyclic and acyclic dienes and either ethylene or acetylene as the dienophile. Table 1 lists the minimum and maximum deviation of the DFT enthalpies relative to the CBS-QB3 enthalpies (which are in excellent accord with experiment). Clearly, all of the DFT methods perform poorly, with significant errors in these simple reaction energies. The exception is the MO6-2X functional, whose errors are only slightly larger than that found with the SCS-MP2 method. Use of a larger basis set (6-311+G(2df,2p)) reduced errors only a small amount.

Table 1. Maximum, minimum and mean deviation of reaction enthalpies (kcal mol^-1) for the reactions in Scheme 1 using the 6-31+G(d,p) basis set.¹

In order to discern where the problem originates, they next explore the changes that occur in the Diels-Alder reaction: two π bonds are transformed into one σ and one π bond and the conjugation of the diene is lost, leading to (proto)branching in the product. Reactions 1-3 are used to assess the energy consequence of converting a π bond into a σ bond, creating a protobranch, and the loss of conjugation, respectively.

The energies of these reactions were then evaluated with the various functionals. It is only with the conversion of the π bond into a σ bond that they find a significant discrepancy between the DFT estimates and the CBS-QB3 estimate. DFT methods overestimate the energy for the π → σ exchange, by typically around 5 kcal mol^-1, but it can be much worse. Relying on cancellation of errors to save the day for DFT will not work when these types of bond changes are involved. Once again, the user of DFT is severely cautioned!

References

(1) Pieniazek, S. N.; Clemente, F. R.; Houk, K. N., "Sources of Error in DFT Computations of C-C Bond Formation Thermochemistries: π → σ Transformations and Error Cancellation by DFT Methods," Angew. Chem. Int. Ed. 2008, 47, 7746-7749, DOI: 10.1002/anie.200801843

While catalysis of many pericyclic reactions have been reported, until now there have been no reports of a catalyzed electrocylization. Bergman, Trauner and coworkers have now identified the use of an aluminum Lewis Acid to catalyze a 6e^– electrocyclization.¹

They start off by noting that electron withdrawing groups on the C₂ position of a triene lowers the barrier of the electrocylization. So they model the carbomethoxy substituted hexatriene (1a-d) with a proton attached to the carbonyl oxygen as the Lewis acid at B3LYP/6-31G**. Table 1 presents the barrier for the four possible isomeric reactions. Only in the case where the substituent is in the 2 position is there a significant reduction in the activation barrier: 10 kcal mol^-1.

Table 1. B3LYP/6-31G** activation barriers (kcal mol^-1) for the catalyzed (H⁺) and uncatalyzed electrocylication reaction of carbomethoxy-substituted hexatrienes.

With these calculations as a guide, they synthesized compounds 3 and 5 and used Me₂AlCl as the catalysts. In both cases, significant rate enhancement was observed. The thermodynamic parameters for these electrocylizations are given in Table 2. The aluminum catalyst acts primarily to lower the enthalpic barrier, as predicted by the DFT computations. The effect is not as dramatic as for the computations due likely to a much greater charge dispersal in over the aluminum catalyst (as opposed to the tiny proton in the computations) and the omission of solvent from the calculations.

Table 2. Experimental thermodynamic parameters for the electrocylcization of 3 and 5.

References

(1) Bishop, L. M.; Barbarow, J. E.; Bergman, R. G.; Trauner, D., "Catalysis of 6π Electrocyclizations," Angew. Chem. Int. Ed. 2008, 47, 8100-8103, DOI: 10.1002/anie.200803336

InChIs

1a: InChI=1/C8H10O2/c1-3-4-5-6-7-8(9)10-2/h3-7H,1H2,2H3/b5-4-,7-6+
InChIKey=INMLJEKOJCNLTL-SCFJQAPRBY

1b: InChI=1/C8H10O2/c1-3-4-5-6-7-8(9)10-2/h3-7H,1H2,2H3/b5-4-,7-6-
InChIKey=INMLJEKOJCNLTL-RZSVFLSABV

1c: InChI=1/C8H10O2/c1-4-5-6-7(2)8(9)10-3/h4-6H,1-2H2,3H3/b6-5-
InChIKey=QALYADPPGKOFPQ-WAYWQWQTBX

1d: InChI=1/C8H10O2/c1-4-6-7(5-2)8(9)10-3/h4-6H,1-2H2,3H3/b7-6+
InChIKey=BRDQFYBEWWPLFX-VOTSOKGWBR

2a: InChI=1/C8H10O2/c1-10-8(9)7-5-3-2-4-6-7/h2-5>,7H,6H2,1H3
InChIKey=LUFUPKXCMNRVLT-UHFFFAOYAU

2c: InChI=1/C8H10O2/c1-10-8(9)7-5-3-2-4-6-7/h2-3,5H,4,6H2,1H3
InChIKey=KPYYGHDMWKXJCE-UHFFFAOYAC

2d: InChI=1/C8H10O2/c1-10-8(9)7-5-3-2-4-6-7/h3,5-6H,2,4H2,1H3
InChIKey=YCTXQIVXFOMZCV-UHFFFAOYAU

3: InChI=1/C17H20O2/c1-5-16(17(18)19-4)14(3)11-13(2)12-15-9-7-6-8-10-15/h5-12H,1-4H3/b13-12+,14-11-,16-5-
InChIKey=DPBZDJWWRAWHQX-USTKDYFJBV

4: InChI=1/C17H20O2/c1-11-10-12(2)16(17(18)19-4)13(3)15(11)14-8-6-5-7-9-14/h5-10,13,15H,1-4H3/t13-,15-/m1/s1
InChIKey=JFBDOBRQORXZEY-UKRRQHHQBP

5: InChI=1/C16H16O/c1-13(12-14-6-3-2-4-7-14)10-11-15-8-5-9-16(15)17/h2-4,6-8,10-12H,5,9H2,1H3/b11-10-,13-12+
InChIKey=OAQIPONHGIZOBU-JPYSRSMKBG

6: InChI=1/C16H16O/c1-11-7-8-13-14(9-10-15(13)17)16(11)12-5-3-2-4-6-12/h2-8,14,16H,9-10H2,1H3/t14-,16-/m0/s1
InChIKey=MJUGKTLVECDOOO-HOCLYGCPBO

Consider bicorannulenyl 1. Each corranulene unit is a bowl and each is chiral due to being monosubstituted. Additional chirality is due to the arrangement of the bowls along the C₁-C_1’ bond, the bond where the two rings join. So both rotation about the C₁-C_1’ bond and bowl inversion will change the local chirality (Scheme 1 distinguishes these two processes.) One might anticipate that the stereodynamics of 1 will be complicated!

Scheme 1

Rabinovitz, Scott, Shenhar and their groups have tackled the stereodynamics of 1.¹ (This is a very nice joint experimental and theoretical study and I wonder why it did not appear in JACS.) At room temperature and above, one observes a single set of signals, a singlet and eight doublets, in the ¹H NMR. Below 200 K, there are three sets of signals, evidently from three different diastereomers.

Each ring can have either P or M symmetry. The authors designate conformations using these symbols for each ring along with the value of the torsion angle about the C₁-C_1’ bond. So, for example, a PP isomer is the enantiomer of the MM conformer when their dihedral angles are of opposite sign.

DFT computations help make sense of these results. PBE0/6-31G* computations reveal all local minima and rotational and inversion transition states of 1. The lowest (free) energy structure is PP₄₄ (see Figure 1). A very small barrier separates it from PP₁₁₁; this barrier is related to loss of conjugation between the two rings. Further rotation must cross a much larger barrier (nearly 17 and 20 kcal mol^-1). These barriers result from the interaction of the C₂ hydrogen of one ring with either the C_2’ or C_10’ hydrogen, similar to the rotational barrier in 1,1’-binaphthyl. However, the barrier is lower in 1 than in 1,1’-binaphthyl due to the non-planar nature of 1 that allows the protons to be farther apart in the TS. Once over these large barriers, two local minima, PP_-45 and PP_-137, separated by a small barrier are again found.

PP44 0.0	PP-28 19.80	PP-45 3.38
PP111 1.54	PP166 16.76	PP-137 0.14

Figure 1. PBE0/6-31G* optimized geometries and relative free energies (kcal mol^-1) of the PP local minima (PP₄₄, PP₁₁₁, PP_-45, and PP_-137) and rotational transition states.¹

The lowest energy bowl inversion transition state (P₄₉) lies 9.6 kcal mole^-1 above PP₄₄. It is shown in Figure 2. The bowl inversion barrier is comparable to that found in other substituted corannulenes,² which are typically about 9-12 kcal mol^-1).

P49 9.58

Figure 2. PBE0/6-31G* optimized geometry and relative free energy of the lowest energy bowl inversion transition state.¹

Interestingly, it is easier to invert the bowl than to rotate about the C₁-C_1’ bond. And this offers an explanation for the experimental ¹H NMR behavior. At low temperature, crossing the low rotational barriers associated with loss of conjugation occurs. So, using the examples from Figure 1, PP₄₄ and PP₁₁₁ appear as a single time-averaged signal in the NMR. This leads to three pairs of enantiomers (S.PP/R.PP, S.MM/R.PP, and S.PM/R.MP), giving rise to the three sets of NMR signals.

References

(1) Eisenberg, D.; Filatov, A. S.; Jackson, E. A.; Rabinovitz, M.; Petrukhina, M. A.; Scott, L. T.; Shenhar, R., "Bicorannulenyl: Stereochemistry of a C40H18 Biaryl Composed of Two Chiral Bowls," J. Am. Chem. Soc. 2008, 73, 6073-6078, DOI: 10.1021/jo800359z.

(2) Wu, Y. T.; Siegel, J. S., "Aromatic Molecular-Bowl Hydrocarbons: Synthetic Derivatives, Their Structures, and Physical Properties," Chem. Rev. 2006, 106, 4843-4867, DOI: 10.1021/cr050554q.

InChIs

1: InChIKey = XZISQKATUXKXQW-UHFFFAOYAG

Angewandte Chemie has published a rather unusual short article – an appeal by Roald Hoffmann, Paul Schleyer and Fritz Schaefer (the latter two were interviewed in my book!) to use “more realism, please!”¹

These noted computational chemists suggest that we all have been sloppy in the language we use in describing our computations. They first take on the term “stable”, and rightfully point out that this is a very contextual term – stable where? on my desktop? In a 1M aqueous solution? Inside a helium glove box? Inside a mass spectrometer? In an interstellar cloud? Stable for how long? Indefinitely? For a day? For a day in the humid weather of San Antonio? Or a day inside a cold refrigerator? Or how about inside a Ne matrix? Or for the time it takes to run a picosecond laser experiment?

The authors offer up the terms “viable” and “fleeting” as reasonable alternatives and proscribe a protocol for meeting the condition of “viable” – and I must note that this protocol is very demanding, likely beyond the computational abilities of many labs and certainly beyond what can be done for a reasonably large molecule.

They also take on the uncertainty of computed results, pointing out the likely largely overlooked irreproducibility of many DFT results, due to size difference of the computed grids, difference in implementation of the supposedly same functional, etc. They conclude with a discussion of how many significant figures one should employ.

None of this is earth-shattering, and most is really well-known yet often neglected or overlooked. In another interesting publication treat in this issue, four referee reports of the article are reproduced. The first, by Gernot Frenking,² argues exactly this point – that the lack of new information, and the sort of whimsical literary approach make the article unacceptable for publication. The other three referees disagree,^3-5 and note that though the article is not novel, the authors forcefully remind us that better behaviors should be put into practice.

The article is a nice reminder that careful studies should be carefully reported. (And both the authors of the article and the referees note that these same comments apply to our experimental colleagues, too.)

References

(1) Hoffmann, R.; Schleyer, P. v. R.; Schaefer III, H. F., “Predicting Molecules – More Realism, Please!,” Angew. Chem. Int. Ed., 2008, 47, 7164-7167, DOI: 10.1002/anie.200801206.

(2) Frenking, G., “No Important Suggestions,” Angew. Chem. Int. Ed. 2008, 47, 7168-7169, doi: 10.1002/anie.200802500.

(3) Koch, W., “Excellent, Valuable, and Entertaining,” Angew. Chem. Int. Ed., 2008, 47, 7170, DOI: 10.1002/anie.200802996.

(4) Reiher, M., “Important for the Definition of Terminology in Computational Chemistry,” Angew. Chem. Int. Ed., 2008, 48, 7171, DOI: 10.1002/anie.200802506.

(5) Bickelhaupt, F. M., “Attractive and Convincing,” Angew. Chem. Int. Ed., 2008, 47, 7172, DOI: 10.1002/anie.200802330.

Schaefer and Allen have applied their focal point method to the question of the benzylic effect in the S_N2 reaction.¹ S_N2 reactions are accelerated when the attack occurs at the benzylic carbon, a well-known phenomenon yet the reason for this remains unclear. The standard textbook-like argument has been that the negative charge built up in the S_N2 transition state can be delocalized into the phenyl ring. However, solution phase Hammett studies are often U-shaped, indicating that both electron donating and withdrawing group accelerate the substitution reaction. (This is usually argued as indicative of a mechanism change from S_N2 to S_N1.)

The focal point method involves a series of very large computations where both basis set size and degree of electron correlation are systematically increased, allowing for an extrapolation to essentially infinite basis set and complete correlation energy. The energy of the transition state (relative to separated reactants) for four simple S_N2 reactions evaluated with the focal point method are listed in Table 1. The barrier for the benzylic substitutions is lower than for the methyl cases, indicative of the benzylic effect.

Table 1. Energy (kcal mol^-1) of the transition state relative to reactants.¹

To answer the question of why the benzylic substitution reactions are faster, they examined the charge distribution evaluated at B3LYP/DZP++. As seen in Table 1, this method does not accurately reproduce the activation barriers, but the errors are not terrible, and the trends are correct.

In Figure 1 are the geometries of the transition states for the reaction of fluoride with methylflouride or benzylfluoride. The NBO atomic charges show that the phenyl ring acquired very little negative charge at the transition state. Rather, the electric potential at the carbon under attack is much more revealing. The potential is significantly more positive for the benzylic carbon than the methyl carbon in both the reactant and transition states.

VC = -405.156 V	VC = -404.379 V

Figure 1. MP2/DZP++ transition states for the reaction of fluoride with methylfluoride and benzylflouride. NBO charges on F and C and the electrostatic potential in Volts.¹

They next examined the reaction of fluoride with a series of para-substituted benzylfluorides. The relation between the Hammet σ constants and the activation energy is fair (r = 0.971). But the relation between the electrostatic potential at the benzylic carbon (in either the reactant or transition state) with the activation energy is excellent (r = 0.994 or 0.998). Thus, they argue that it is the increased electrostatic potential at the benzylic carbon that accounts for the increased rate of the S_N2 reaction.

References

(1) Galabov, B.; Nikolova, V.; Wilke, J. J.; Schaefer III, H. F.; Allen, W. D., "Origin of the S_N2 Benzylic Effect," J. Am. Chem. Soc., 2008, 130, 9887-9896, DOI: 10.1021/ja802246y.