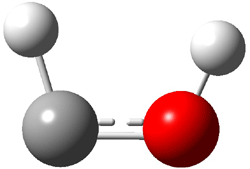
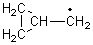The very simple carbene hydroxymethylene, HOCH, has finally been prepared and characterized.¹ Glyoxylic acid CHOCO₂H is subjected to high-vacuum laser photolysis. It fragments into HOCH, which is then trapped into an argon matrix. The experimental IR frequencies match up very well with the CCSD(T)/cc-pVQZ harmonic frequencies of the trans isomer 1t that are also adjusted for anharmonic effects. The computed vertical excitation energy of 415 nm matches well with the experimental value of the maximum absorption in the UV/vis spectra of 427 nm.

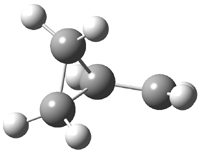
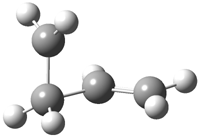
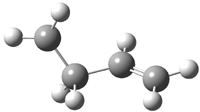
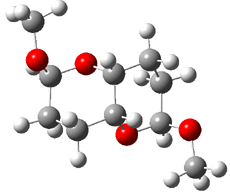
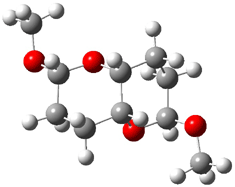
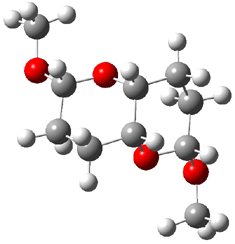
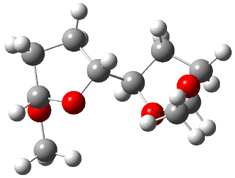
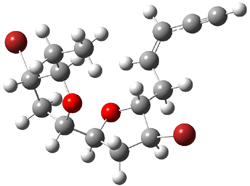
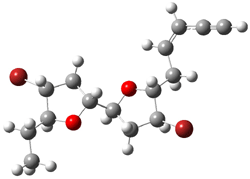
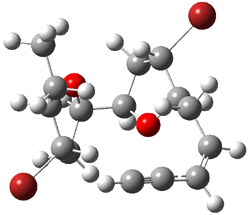
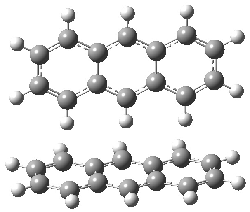
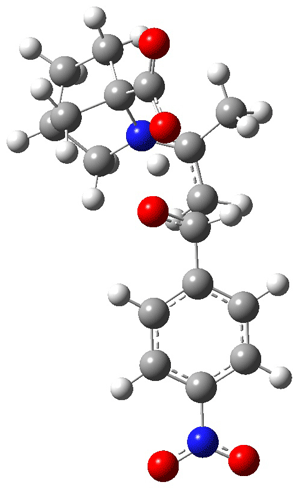
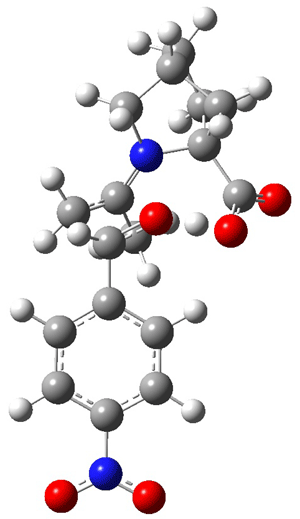
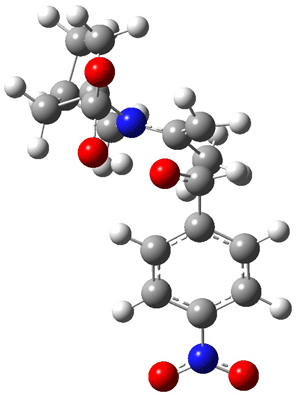
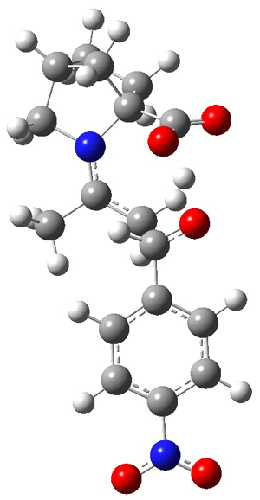
The other very interesting experimental result is that HOCH has a lifetime of about 2 hours in the matrix, while the deuterated species DOCH is stable. To explain these results, Schreiner, Allen and co-workers optimized a number of structures on the PES at CCSD(T)/cc-pVQZ and computed their energies using the focal point technique. The optimized structures and their relative energies are given in Figure 1.

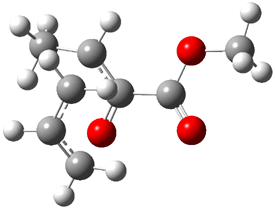
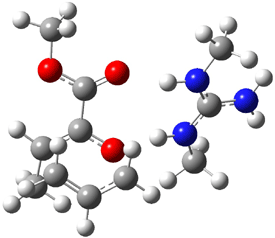
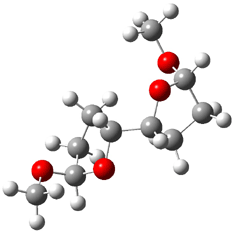
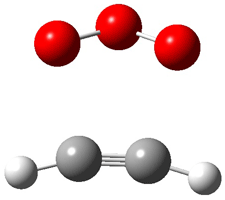
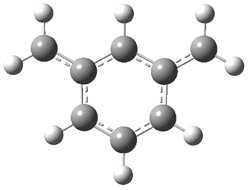
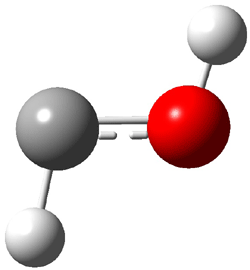
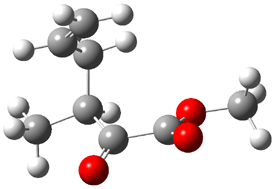
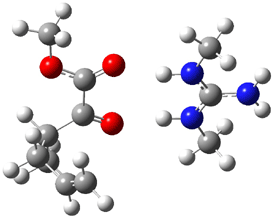
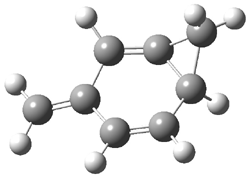
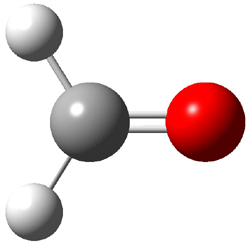
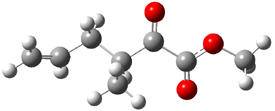
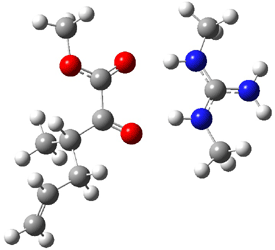
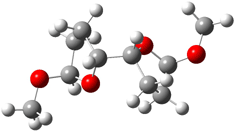
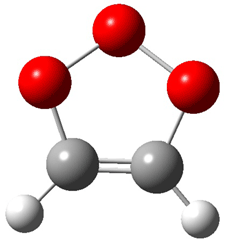
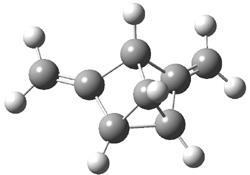
1t (0.0)	TS2 (29.7)	2 (-52.1)
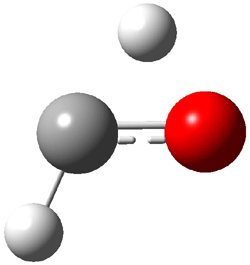
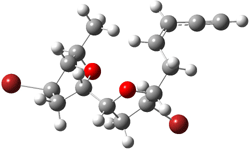
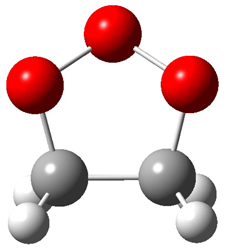
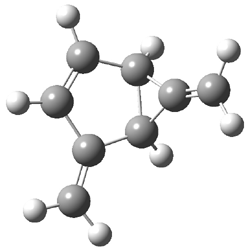
TS1(26.8)
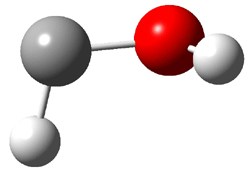
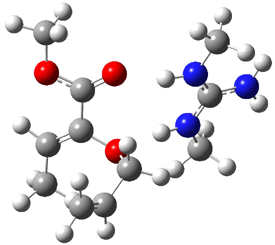
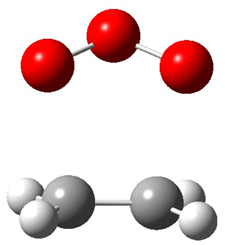
1c (4.4)

Figure 1. Optimized CCSD(T)/cc-pVQZ structures of HOCH isomers and their Focal Point relative energies (kcal mol^-1).¹

The barriers for rearrangement from 1t are both very high. Rearrangement to formaldehyde 2 requires crossing a barrier of 29.7 kcal mol^-1, while the barrier to convert to the cis isomer 1c is 26.8 kcal mol^-1. (Note that from 1c a cleavage into CO and H2 can occur, but this barrier is another 47.0 kcal mol^-1.) These barriers are too large to be crossed at the very low temperatures of the matrices. However, using the intrinsic reaction potential at CCSD(T)/cc-pVQZ and WKB theory, the tunneling lifetime of HOCH is computed to be 122 minutes, in excellent accord with the experiment. The lifetime for DOCH is computed to be over 1200 years. Thus, the degradation of hydroxymethylene is entirely due to tunneling through a very large classical barrier! This rapid tunneling casts serious doubt on the ability to ever identify any hydroxymethylene in interstellar space.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard IV, F. C.; Simmonett, A. C.; Allen, W.
D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

InChI

1: InChI=1/CH2O/c1-2/h1-2H
2: InChI=1/CH2O/c1-2/h1H2

There remains still new territory to explore even with such well-known reactions as the Claisen rearrangement. Jacobsen reports a catalyzed Claisen rearrangement where the catalyst is urea-based.¹ Catalyst 1 produces modest to very reasonable % conversion in a series of simple Claisen rearrangements, as shown in Table 1.

Table 1. Claisen Rearrangements

With the chiral catalyst 2, the Claisen rearrangement is both catalyzed and proceeds with large enantiomeric excess, as shown in the representative example Reaction 1.

Jacobsen and Uyeda also reported the transition state for a model Claisen rearrangement catalyzed by a model guanidinium ion (Reaction 2) computed at B3LYP/6-31G(d). I have reproduced this calculation and the calculations for the both the catalyzed and uncatalyzed rearrangements, shown in Figure 1. In email communication with Dr. Jacobsen, I was able to confirm these energies against their own unpublished results.

Uncatalyzed Reaction 2
Reactant: 0.0	TS: 25.73
Product 1: -11.04	Product 2: -13.69
Catalyzed Reaction 2
Reactant: 0.0	TS: 21.09
Product 1: -12.36	Product 2: -12.80

Figure 1. B3LYP/6-31G(d) optimized structures of the critical points of uncatalyzed and catalyzed Reaction 2. Relative energies in kcal mol^-1.

The structures show the beneficial hydrogen bonds between the guanidinium anion and the carbonyl oxygens (or the ether oxygen of the reactant). In progressing from the transition state, both reactions first gives Product 1. This product conformer can than rotate to give the lower energy conformer Product 2. The activation energy of the catalyzed reaction is 4.64 kcal mol^-1 lower than for the uncatalyzed reaction, demonstrating the benefit of the complexation in the transition state.

I want to thank Dr. Jacobsen and his graduate student Chris Uyeda for sharing their computational results with me for the preparation of this blog post.

References

(1) Uyeda, C.; Jacobsen, E. N., "Enantioselective Claisen Rearrangements with a Hydrogen-Bond Donor Catalyst," J. Am. Chem. Soc., 2008, 130, 9228-9229, DOI: 10.1021/ja803370x.

Bickelhaupt has reported a broad benchmark study of the prototype S_N2 and E2 reactions.¹ These are the reactions of ethyl fluoride with fluoride and ethyl chloride with chloride (Scheme A). The critical points were optimized at OLYP/TZ2P and then CCSD(T)/CBS energies are used as benchmark. A variety of different density functionals were then used to obtain single-point energies.

Scheme A

The relative energies of the transition states for the six different reactions are listed for some of the functionals in Table 1. (These are energies relative to separated reactants – and keep in mind that an ion dipole complex is formed between the reactants and the transition states – Bickelhaupt calls this a “reaction complex”.)

Table 1. Relative energies (kcal mol^-1) of the transition states for the six reactions shown in Scheme A.

There is a lot more data in this paper, along with a summary of the mean absolute errors in the overall and central barriers that mimics the data I show in Table 1. The trends are pretty clear. Generalized gradient approximation (GGA) functions – like BLYP, PW91, and PBE – dramatically underestimate the barriers. The hybrid functionals perform much better. The recently maligned B3LYP functional gets the correct trend and provides reasonable estimates of the barriers. Truhlar’s MO5-2X and MO6-2X functionals do very well in matching up the barrier heights along with getting the correct trends in the relative barriers. Simply looking for the functional with the lowest absolute error is not sufficient; BHandH and MO6-L have small errors but give a wrong trend in barriers, predicting that the S_N2 reaction is preferred over the E2 for the fluoride reaction.

Reference

(1) Bento, A. P.; Sola, M.; Bickelhaupt, F. M., "E2 and S_N2 Reactions of X^– + CH₃CH₂X (X = F, Cl); an ab Initio and DFT Benchmark Study," J. Chem. Theory Comput., 2008, 4, 929-940, DOI: 10.1021/ct700318e.

Wes Borden has been exploring reactions where tunneling is operational. These studies have been inspired by Bill Doering’s¹ statement regarding tunneling in 1,5-sigmatropic shifts: “The tunneling effect is likely, in the opinion of some, to remain relegated to the virtual world of calculations”. Borden’s first two papers dealt with the kinetic isotope effects for the [1,5]-H shift in 1,3-cyclopentadiene and 5-methyl-1,3-cyclopentadiene.^2,3

His latest article examines carbon tunneling,⁴ which, due to the much heavier mass of the carbon nucleus relative to a proton, is likely to play a minimal role at best. Borden looked at the ring opening of cyclopropylcarbinyl radical 1 to 3-butene-1-yl radical 2, passing through transition state TS1-2. The B3LYP/6-31G(d) optimized structures are shown in Figure 1.

1		2
1	TS1-2	2

Figure 1. B3LYP/6-31G(d) optimized geometries of 1, 2, and TS1-2.⁴

The predicted rate of the reaction at 298 K using canonical variational transition state theory is increased by about 50% when small-curvature tunneling is included. This predicted rate is a bit smaller than the experimental value. Experiments also shows a linear Arrhenius plot, and Borden’s calculations agree until one reaches very low temperatures. Below 150 K the Arrhenius curve begins to deviate from linearity, and below 20 K the curve is flat – the rate is no longer temperature dependent! Thus, at cryogenic temperatures, the tunneling rate far exceeds traditional crossing of the variational barrier. Borden hopes that experimentalists will reinvestigate this problem (and hopefully confirm his predictions).

References

(1) Doering, W. v. E.; Zhao, X., "Effect on Kinetics by Deuterium in the 1,5-Hydrogen Shift of a Cisoid-Locked 1,3(Z)-Pentadiene, 2-Methyl-10-methylenebicycloJ. Am. Chem. Soc., 2006, 128, 9080-9085, DOI: 10.1021/ja057377v.

(2) Shelton, G. R.; Hrovat, D. A.; Borden, W. T., "Tunneling in the 1,5-Hydrogen Shift Reactions of 1,3-Cyclopentadiene and 5-Methyl-1,3-Cyclopentadiene," J. Am. Chem. Soc., 2007, 129, 164-168, DOI: 10.1021/ja0664279.

(3) Shelton, G. R.; Hrovat, D. A.; Borden, W. T., "Calculations of the Effect of Tunneling on the Swain-Schaad Exponents (SSEs) for the 1,5-Hydrogen Shift in 5-Methyl-1,3-cyclopentadiene. Can SSEs Be Used to Diagnose the Occurrence of Tunneling?," J. Am. Chem. Soc., 2007, 129, 16115-16118, DOI: 10.1021/ja076132a.

(4) Datta, A.; Hrovat, D. A.; Borden, W. T., "Calculations Predict Rapid Tunneling by Carbon from the Vibrational Ground State in the Ring Opening of Cyclopropylcarbinyl Radical at Cryogenic Temperatures," J. Am. Chem. Soc., 2008, 130, 6684-6685, DOI: 10.1021/ja801089p.

InChIs

1: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2

2: InChI=1/C4H7/c1-3-4-2/h3H,1-2,4H2

The search for the elusive hypervalent carbon atom took an interesting turn for the positive with the report of the synthesis and characterization of 1 and especially its dication 2.¹ The x-ray structure was obtained for both compounds along with computing their B3PW91/6-31G(d) geometries. These computed geometries are shown in Figure 1.

1	2
1	2

Figure 1. B3PW91/6-31G(d) optimized geometries of 1 and 2.¹

The allene fragment is bent in both structures: 168.5° (169.9° at B3PW91) in 1 and 166.8° (172.7° at B3PW91) in 2. The distances between the central carbon atom of the allene and the four oxygen atoms are 2.66 to 2.82 Å, and computed to be a little longer. Interestingly, these distance contract when the dication 2 is created; ranging from 2.64 to 2.75 Å (again computed to be a little longer). These distances, while significantly longer than normal covalent C-O bonds, are less than the sum of the C and O van der Waals radii. But are they really bonds?

This is not a trivial answer to solve. The authors opt to employ topological electron density analysis (Bader’s atoms-in-molecules approach). Using the electron density from both the high resolution x-ray density map and from the DFT computations, bond paths between the central allene carbon and each oxygen are found, though with, as expected, low values of ρ. The Laplacian of the density at the critical point are positive, indicative of ionic interactions. So according to Bader’s model, the existence of a bond path in a ground state molecule is the necessary and sufficient condition for bonding.

The others conclude by proposing that O^…C intermolecular interactions with separations of around 2.6 to 2.8 Å may also suggest hypervalent cases. They note that about 2000 structures in the Cambridge crystallographic database fit this criterion.

References

(1) Yamaguchi, T.; Yamamoto, Y.; Kinoshita, D.; Akiba, K.-y.; Zhang, Y.; Reed, C. A.; Hashizume, D.; Iwasaki, F., "Synthesis and Structure of a Hexacoordinate
Carbon Compound," J. Am. Chem. Soc., 2008, 130, 6894-6895, DOI: 10.1021/ja710423d.

InChIs

1: InChI=1/C31H24O4S2/c1-32-20-9-5-13-24-28(20)18(29-21(33-2)10-6-14-25(29)36-24)17-19-30-22(34-3)11-7-15-26(30)37-27-16-8-12-23(35-4)31(19)27/h5-16H,1-4H3
InChiKey= RJBVLFYVIBCWKW-UHFFFAOYAD

2: InChI=1/C33H30O4S2/c1-34-22-11-7-15-26-30(22)20(31-23(35-2)12-8-16-27(31)38(26)5)19-21-32-24(36-3)13-9-17-28(32)39(6)29-18-10-14-25(37-4)33(21)29/h7-18H,1-6H3/q+2
InChIKey= MVHOSIVPHPDYJJ-UHFFFAOYAM

At the Spring ACS meeting in New Orleans this past April, Jonathan Goodman told me about his group’s new work on computed NMR spectra. This study has now appeared.¹ The new aspect of this work is taking on compounds with significant conformational flexibility. They first examined the bifuranyl- and pyranopyrans acetals 1-6.

They identified all energetically low-lying conformers through a Monte Carlo MM search, and reoptimized the structures at B3LYP/6-31G**. PCM energies, with the dielectric set to 4.81 to simulate CHCl₃, were obtained using the gas-phase geometries. ¹³C NMR shifts were then computed and weighted based on Boltzmann averaging. Compounds 4-7 require consideration of 4, 5, or 7 conformations, respectively, to account for at least 95% of the population. (The lowest energy conformation for each compound is displayed in Figure 1.) The computed ¹³C NMR chemical shifts were then compared against the experimental values that have been obtained for 5 of these 6 compounds, though it was not known which experimental spectra corresponds with which structure. Based on the correlation coefficients and the mean and maximum values of the differences between the calculated and experimental shifts allows for identification of the structure that corresponds to each of the five spectra.

1	2	3
4	5	6

Figure 1. B3LYP/6-31G** minimum energy conformation of 1-6.¹

They next took on the absolute structure of elatenyne 7. This compound has been isolated and its ¹³C NMR obtained nd interpreted.² The compound can exist in one of 32 different diastereomers. Instead of having to stereospecifically synthesize each diastereomer, obtain its NMR spectra and compare with the natural product, Goodman suggests that one can compute the ¹³C NMR spectra for each isomer, identified the likely candidates, and synthesize just those if verification is necessary. So, they computed the spectra of all 32 isomers following the above prescription. The chemical shifts for the carbons bearing bromine have relatively large errors, though these can by systematically corrected by reducing the computed values by about 20 ppm. Comparison of the computed spectra of each isomer with the experimental spectra gave three possible isomers (7a-c, see Figure 2) with very strong correlation coefficients. Examination of the men value of the difference of the computed chemical shifts with the experimental values (not including the carbon atoms with a bromine attached) suggests one more possibility 7d (see Figure 2).

7
7a	7b
7c	7d

Figure 2. B3LYP/6-31G** minimum energy conformation of 7a-d.¹

References

(1) Smith, S. G.; Paton, R. S.; Burton, J. W.; Goodman, J. M., "Stereostructure Assignment
of Flexible Five-Membered Rings by GIAO 13C NMR Calculations: Prediction of the Stereochemistry of Elatenyne," J. Org. Chem., 2008, DOI: 10.1021/jo8003138.

(2) Sheldrake, H. M.; Jamieson, C.; Burton, J. W., “The Changing Faces of Halogenated Marine Natural Products: Total Synthesis of the Reported Structures of Elatenyne and an Enyne from Laurencia majuscula,” Angew. Chem. Int. Ed., 2006, 45, 7199-7202, DOI: 10.1002/anie.200602211

InChIs

1-3: InChI=1/C10H18O4/c1-11-9-5-3-8-7(13-9)4-6-10(12-2)14-8/h7-10H,3-6H2,1-2H3

4-6: InChI=1/C10H18O4/c1-11-9-5-3-7(13-9)8-4-6-10(12-2)14-8/h7-10H,3-6H2,1-2H3

7: InChI=1/C15H20Br2O2/c1-3-5-6-7-13-11(17)9-15(19-13)14-8-10(16)12(4-2)18-14/h1,5-6,10-15H,4,7-9H2,2H3/b6-5-
InChIKey=SKSTYQSRJPCZSW-WAYWQWQTBQ

The importance of the interactions between neighboring aromatic molecules cannot be overemphasized – π-π-stacking is invoked to explain the structure of DNA, the hydrophobic effect, molecular recognition, etc. Nonetheless, the nature of this interaction is not clear. In fact the commonly held notion of π-π orbital overlap is not seen in computations.

Grimme¹ has now carefully examined the nature of aromatic stacking by comparison with aliphatic analogues. He has examined dimers formed of benzene 1, naphthalene 2, anthracene 3, and teracene 4 and compared these with the dimers of their saturated analogues (cyclohexane 1s, decalin 2s, tetradecahydroanthracene 3s, and octadecahydrotetracene 4s. The aromatic dimmers were optimized in the T-shaped and stacked arrangements, and these are shown for 3 along with the dimer of 3s in Figure 1. These structures are optimized at B97-D/TZV(2d,2p) – a functional designed for van der Waals compounds. Energies were then computed at B2LYP-D/QZV3P, double-hybrid functional that works very well for large systems.

Figure 1. Optimized structures of 3s, 3t, and 3a.

The energies for formation of the complexes are listed in Table 1. The first interesting result here is that the benzene and naphthalene dimmers (whether stacked or T-shaped) are bound by about the same amount as their saturated analogues. Grimme thus warns that “caution is required to not overestimate the effect of the π system”.

Table 1. Complexation energy (kcal mol^-1)

The two larger aromatics here do show a significantly enhanced complexation energy than their saturated analogues, and Grimme refers to this extra stabilization as the π-π stacking effect (PSE). Energy decomposition analysis suggests that electrostatic interactions actually favor the complexation of the saturated analogues over the aromatics. However, Pauli exchange repulsion essentially cancels the electrostatic attraction for all the systems, and it is dispersion that accounts for the dimerization energy. Dispersion increases with size of the molecule, and “classical” dispersion forces (the R^-6 relationship) accounts for more than half of the dispersion energy in the saturated dimmers, while it is the non-classical, or orbital-based, dispersion that dominates in the stacked aromatic dimmers. Grimme attributes this to “special nonlocal electron correlations between the π electrons in the two fragments at small interplane distances”.

References

(1) Grimme, S., "Do Special Noncovalent π-π Stacking Interactions Really Exist?," Angew. Chem. Int. Ed., 2008, 47, 3430-3434, DOI: 10.1002/anie.200705157.

InChIs

1: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H

1s: InChI=1/C6H12/c1-2-4-6-5-3-1/h1-6H2

2: InChI=1/C10H8/c1-2-6-10-8-4-3-7-9(10)5-1/h1-8H

2s: InChI=1/C10H18/c1-2-6-10-8-4-3-7-9(10)5-1/h9-10H,1-8H2

3: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H

3s: InChI=1/C14H24/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h11-14H,1-10H2

4: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

4s: InChI=1/C18H30/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h13-18H,1-12H2

The composite methods (exemplified by the Gaussian-n methods, the Weizmann-n methods and CNS-Q methods) are popularly held to be perhaps the best (if not the most straightforward and mechanical) procedures for obtaining accurate energetics. Errors are generally thought to be in the 1-2 kcal mol^-1 range – quite suitable for comparisons with experiment. The recent study of the 1,3-dipolar cycloaddition of ozone with ethene or ethyne offers serious food for thought about considering these composite methods as simple “black-box” solutions towards obtaining good results.
Wheeler, Ess, and Houk have examined the cycloaddition of ozone with ethyne (Reaction 1) and ethane (Reaction 2) with a variety of different computational techniques.¹ Shown in Figure 1 are the CCSD(T)/cc-pVTZ optimized geometries of the pre-complex, transition state and product for both reactions. One of the potential challenges of these reactions is that ozone has appreciable radical character which is also likely to be true in the pre-complex and transition state but the product should have little to no radical character.

Reaction 1
Precomplex	TS	Product
Reaction 2
Precomplex	TS	Product

The relative enthalphies (0K) of the complex, TS and product were computed using a number of different composite methods. The CBS-QB3, G3, G3B3, G3MP2B3 and G4^2,3 results are listed in Table 1 for both reactions. All of these methods claim a small error – perhaps 1-2 kcal mol^-1. The Gaussian-n methods nicely cluster for the reaction energy for both reactions, while CBS-QB3 predicts both reactions are more exothermic. (The same is also true of CBS-APNO.) The G-n methods indicate that the precomplex is essentially unbound. More concerning is the spread in the enthalpy values of the reaction barrier: the G-n methods predict a barrier that ranges over 5 kcal mol^-1.

Table 1. Relative enthalpies (kcal mol^-1) of the critical points for Reactions 1 and 2.¹

So what is the correct barrier height? A focal point extrapolation procedure was then performed. This seeks to extrapolate to infinite basis set and estimate the effects of correlation through CCSDT(Q) and includes corrections for the Born-Oppenheimer approximation and special relativistic effects. The focal point results are also shown in Table 1. The new G4 composite method gives enthalpies in very nice agreement with those obtained with the much more expensive focal point procedure. However, the other composite methods fair much worse, especially for the activation barrier.
The convergence of the focal point method for the reaction energy is slow, leading to a large error bar of 2 kcal mol^-1. This appears to relate to the radical character difference between the reactant and product. The convergence for the activation barrier is much better (an error of only 0.2 kcal mol^-1) and here the comparison is between reactant and TS which have similar radical character.
Perhaps the most discouraging aspect of this study is that the relative energy predicted using the highest computational component of the composite method – so, CCSD(T)/6-31+G* for the CBS-QB3 method and QCISD(T)/6-31G(d) for the G3 methods – are more accurate than the composite method itself. But, the reasonable performance of the new G4 method^2,3 does offer some glimmer of hope here.

References

(1) Wheeler, S. E.; Ess, D. H.; Houk, K. N., "Thinking
Out of the Black Box: Accurate Barrier Heights of 1,3-Dipolar Cycloadditions of Ozone with Acetylene and Ethylene," J. Phys. Chem. A, 2008, 112, 1798-1807, DOI: 10.1021/jp710104d.

(2) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory," J. Chem. Phys., 2007, 126, 084108, DOI: 10.1063/1.2436888

(3) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory using
reduced order perturbation theory," J. Chem. Phys., 2007, 127, 124105-8, DOI: 10.1063/1.2770701.

InChIs

Reaction 1 product: InChI=1/C2H2O3/c1-2-4-5-3-1/h1-2H

Reaction 2 product: InChI=1/C2H4O3/c1-2-4-5-3-1/h1-2H2

The photochemistry of m-xylylene 2 has been studied by Sander¹ and, as might be anticipated, it’s fascinating! Flash vapor pyrolysis of 1 produces 2. Photolysis of 2 at wavelengths above 400nm gives 3 and 4, while photolysis at 254 nm gives 5. These are products are novel strained hydrocarbons. Confirmation of their structures was obtained by comparing their experimental IR spectra with that computed at B3LYP/6-311G(d,p). Table 1 compares the experimental and computed IR absorptions for 2-5. Note in particular the fine agreement between the two, especially the predicted changes due to i>d₄ substitution for all the phenyl positions.

Table 1. Experimental and Calculated vibrational frequencies (cm^-1) of 2-5.¹

The computed structures of 2-5 and their relative energies are shown in Figure 1. Triplet 1 is the lowest energy isomer, with the singlet-triplet gap of 6.22 kcal mol^-1. This compares with recent high-level computations which give a value of 13.8 kcal mol^-1. ² The other structures are much higher in energy. These other isomers have unusual bonding environments – 3 contains the strained methylenecyclopropane group, 4 is an anti-Bredt compound, and 5 is a very strained tricycle. These compounds can only be prepared by the application of light to provide the energy needed for their creation.

2 Triplet 0.0 Singlet 6.22	3 19.20
4 25.74	5 48.64

Figure 1. B3LYP/6-311G(d,p) optimized structures of 2-5 and their relative energies (kcal mol^-1).¹

References

(1) Neuhaus, P.; Grote, D.; Sander, W., "Matrix Isolation, Spectroscopic Characterization, and Photoisomerization of m-Xylylene," J. Am. Chem. Soc., 2008, 130, 2993-3000, DOI: 10.1021/ja073453d.

(2) Wang, T.; Krylov, A. I., "The effect of substituents on electronic states’ ordering in meta-xylylene diradicals: Qualitative insights from quantitative studies," J. Chem. Phys., 2005, 123, 104304, DOI: 10.1063/1.2018645.

InChIs

2: InChI=1/C8H8/c1-7-4-3-5-8(2)6-7/h3-6H

3: InChI=1/C8H8/c1-5-3-4-7-6(2)8(5)7/h3-4,7-8H,1-2H2; InChIKey=IAJQBWKVTDKBHW-UHFFFAOYAA

4: InChI=1/C8H8/c1-6-2-3-7-5-8(7)4-6/h2-4,7H,1,5H2; InChIKey=XSFFUTQMPAAWHN-UHFFFAOYAU

5: InChI=1/C8H8/c1-3-5-4(2)7-6(3)8(5)7/h5-8H,1-2H2; InChIKey=USZJYFGTTGREFL-UHFFFAOYAB

In Chapter 5.3.2, I extensively discuss the organocatalyzed aldol reaction. Barbas and List have pioneered the use of proline to catalyze this reaction, and Houk has performed a series of computational studies to discern the mechanism. The mechanism is essentially the attack of the enamine on the carbonyl with concomitant proton transfer from the carboxylic acid to the forming oxyanion.

Shininisha and Sunoj have examined a number of bicyclic analogues of proline (1-11) as catalysts of the aldol reaction.¹ They computed the activation energies for the reaction of the enamine derived from acetone with p-nitrobenzaldehyde with the various catalysts. All computations were performed at B3LYP/6-311+G**//B3LYP/6-31G* with the solvent effects modeled using CPCM.

As Houk has demonstrated, there are four possible transition states: the attack can come to either the re or si face of the aldehyde and either the syn or anti enamine can be the reactant. The four transition states for the reaction of 8 are shown in Figure 1. These TSs are representative of all of the transition states involving the different catalysts, including proline itself. These TS are characterized by proton transfer accompanying the C-C bond formation. Their relative energies can be interpreted in terms of the distortions about the enamine double bond (the more planar, the lower the energy) and the arrangement of the carboxylic acid and the incipient oxyanion. These arguments were made by Houk and are described in my book.

8-anti-re 0.0	8-anti-si 2.12
8-syn-re 8.15	8-syn-si 7.28

Figure 1. B3LYP/6-311+G**//B3LYP/6-31G* optimized structures and relative energies (kcal/mol) of the transition states of the enamine derived from acetone and 8 with p-nitrobenzaldehyde¹

The enantiomeric excess predicted by the computations for the aldol reaction using the 11 different bicyclic catalysts is presented in Table 1. All of the catalysts except 11 give high enantiomeric excess, with a number of them predicted to produce an ee above 90%. The authors conclude that these catalysts are worth exploring, since they are predicted to perform better than proline (which has a predicted ee of 75%).

Table 1. Predicted ee for the reaction of the enamine derived
from acetone and catalyst with p-nitrobenzaldehyde.

References

(1) Shinisha, C. B.; Sunoj, R. B., "Bicyclic Proline Analogues as Organocatalysts for Stereoselective Aldol Reactions: an in silico DFT Study," Org. Biomol. Chem., 2007, 5, 1287-1294, DOI: 10.1039/b701688c.

InChIs

1: InChI=1/C8H13NO2/c1-5-4-6-2-3-8(5,9-6)7(10)11/h5-6,9H,2-4H2,1H3,(H,10,11)

2: InChI=1/C8H13NO2/c1-5-4-8(7(10)11)3-2-6(5)9-8/h5-6,9H,2-4H2,1H3,(H,10,11)

3: InChI=1/C6H9NO2/c8-5(9)6-2-1-4(3-6)7-6/h4,7H,1-3H2,(H,8,9)

4: InChI=1/C6H9NO3/c8-5(9)6-2-1-4(7-6)10-3-6/h4

5: InChI=1/C5H7NO3/c7-4(8)5-1-3(6-5)9-2-5/h3,6H,1-2H2,(H,7,8)

6: InChI=1/C6H9NO2S/c8-5(9)6-2-1-4(7-6)10-3-6/h4,7H,1-3H2,(H,8,9)

7: InChI=1/C5H7NO2S/c7-4(8)5-1-3(6-5)9-2-5/h3,6H,1-2H2,(H,7,8)

8: InChI=1/C7H11NO2/c9-6(10)7-2-1-5(3-7)4-8-7/h5,8H,1-4H2,(H,9,10)

9: InChI=1/C7H11NO2/c9-7(10)6-4-1-2-5(3-4)8-6/h4-6,8H,1-3H2,(H,9,10)

10: InChI=1/C6H9NO2/c8-6(9)5-3-1-4(2-3)7-5/h3-5,7H,1-2H2,(H,8,9)

11: InChI=1/C6H9NO2/c8-6(9)5-3-1-4(5)7-2-3/h3-5,7H,1-2H2,(H,8,9)