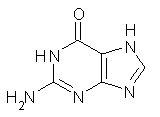
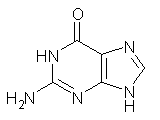
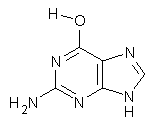
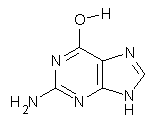
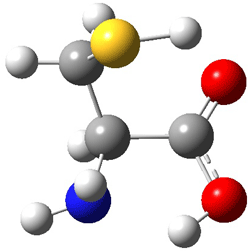
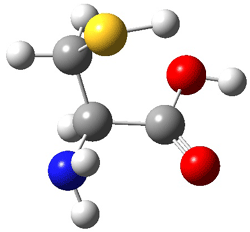
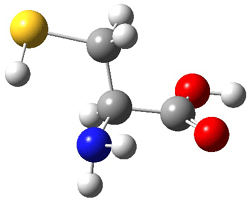
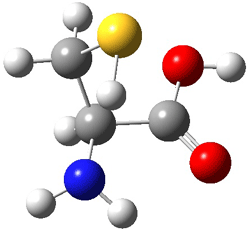
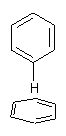
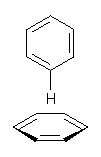
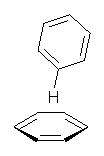
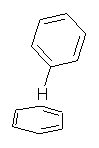
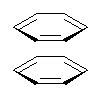
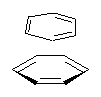
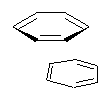
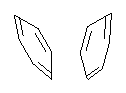
Here’s another fine paper from the Alonso group employing laser ablation molecular beam Fourier transform microwave spectroscopy coupled with computation to discern molecular structure. In this work they examine the low-energy tautomers of guanine.1 The four lowest energy guanine tautomers are shown in Figure 1. (Unfortunately, Alonso does not include the optimized coordinates of these structures in the supporting information – we need to more vigorously police this during the review process!) These tautomers are predicted to be very close in energy (MP2/6-311++G(d,p), and so one might expect to see multiple signals in the microwave originating from all four tautomers. In fact, they discern all four, and the agreement between the computed and experimental rotational constants are excellent (Table 1), especially if one applies a scaling factor of 1.004. Once again, this group shows the power of combined experiment and computations!

Figure 1. Four lowest energy (kcal mol^-1, MP2/6-311++G(d,p)) tautomers of guanine.

Table 1. Experimental and computed rotational constants (MHz) of the four guanine tautomers.

References

(1) Alonso, J. L.; Peña, I.; López, J. C.; Vaquero, V., "Rotational Spectral Signatures of Four Tautomers of Guanine," Angew. Chem. Int. Ed. 2009, 48, 6141-6143, DOI: 10.1002/anie.200901462

InChIs

Guanine: InChI=1/C5H5N5O/c6-5-9-3-2(4(11)10-5)7-1-8-3/h1H,(H4,6,7,8,9,10,11)/f/h8,10H,6H2
InChIKey=UYTPUPDQBNUYGX-GSQBSFCVCX

I have written a number of blog posts that deal with the computation of optical activity. Trindle and Altun have now reported TD-DFT computations of circular dichroism of high-symmetry molecules.¹ The employ either B3LYP (with a variety of basis sets, the largest being 6-311++G(2d,2p)) and SOAP/ATZP. For a number of the high symmetry molecules (two examples are shown in Figure 1), the two methods differ a bit in their predictions of the first excited state, with SOAP typically predicting a red shift relative to the B3LYP. However, both methods general give the same sign of the CD signals and their line shapes are similar.

1	2

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2 (again due to incomplete supporting materials, I reoptimized these structures)

References

(1) Trindle, C.; Altun, Z., "Circular dichroism of some high-symmetry chiral molecules: B3LYP and SAOP calculations " Theor. Chem. Acc. 2009, 122, 145-155, DOI: 10.1007/s00214-008-0494-8.

InChIs

1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2
InChIKey=DYZSIUYFWKNLHS-UHFFFAOYAB

2: InChI=1/C20H24/c1-13-9-18-7-8-20-12-15(3)19(11-16(20)4)6-5-17(13)10-14(18)2/h9-12H,5-8H2,1-4H3
InChIKey=JTMLLDPOLFRPGJ-UHFFFAOYAC

DFT &Optical Rotation Steven Bachrach 27 Jul 2009 No Comments

I (0.0)	II (4.79)
III (5.81)	IV (5.95)

Figure 1. MP2(FC)/aug-cc-pV(T+d)Z optimized geometries and focal point relative energies (kJ mol^-1) of the four lowest energy conformers of cysteine.¹

The three lowest energy structures found here match up with the lowest two structures found by Alonso and the energy differences are also quite comparable: 4.79 kJ and 5.81 mol^-1 with the focal point method 3.89 and 5.38 kJ mol^-1 with MP4/6-311++G(d,p)// MP2/6-311++G(d,p). So the identification of the cysteine conformers made by Alonso remains on firm ground.

References

(1) Wilke, J. J.; Lind, M. C.; Schaefer, H. F.; Csaszar, A. G.; Allen, W. D., "Conformers of Gaseous Cysteine," J. Chem. Theory Comput. 2009, DOI: 10.1021/ct900005c.

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, 4, 6216-6220, DOI: 10.1002/anie.200801337

InChIs

Cysteine:
InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

Back when I was first learning ab initio methods in Cliff Dykstra’s lab, I played a bit with the post-HF method CEPA (couple electron pair approximation). This method fell out of favor over the years with the rise of MP theory and then with DFT. Now, Neese and Grimme and co-workers are resurrecting it.¹ Their Accounts article provides a series of tests of CEPA/1 against benchmark computations (typically CCSD(T)) and lo and behold, CEPA performs remarkably well! It bests B3LYP (no surprise there), B2LYP and MP2 in virtually every category, ranging from reaction energies, hydrogen bond energies, van der Waals interaction energies, and activation barrier heights. As an example, for the isomerization energy of toluene to norbornadiene, CCSD(T) estimates the energy is 42.79 kcal mol^-1. B3LYP does miserably, with an error of nearly 14 kcal mol^-1, but the CEPA/1 estimate is off by only 0.04 kcal mol^-1. Since the computational time of CEPA/1 is competitive with MP2, the authors conclude that CEPA/1 is well-worth reinvestigating as an alternative post-HF methodology.

References

(1) Neese, F.; Hansen, A.; Wennmohs, F.; Grimme, S., "Accurate Theoretical Chemistry with Coupled Pair Models," Acc. Chem. Res. 2009, 42, 641-648 DOI: 10.1021/ar800241t.

Computed NMR spectra have been a major theme of the blog (see these posts). General consensus is that they can be enormously helpful in characterizing structures and stereochemistry, but there has been a nagging sense that one needs to use very large basis sets to get reasonable accuracies.

Bally and Rablen¹ now confront that claim and suggest instead that quite modest basis sets along with a number of flavors of DFT can provide very good ¹H NMR shifts. They examined 80 organic molecules spanning a variety of functional groups. A key feature is that these molecules exist as a single conformation or their conformational distribution is dominated by one conformer. This avoids the need of computing a large number of conformers and taking a Boltzman average of their shifts – a task that would likely require a much larger basis set than what they hope to get away with.

The most important conclusion: the WP04 functional,² developed by Cramer to predict proton spectra, with the very small 6-31G(d,p) basis set and incorporation of the solvent through PCM provides excellent cost/benefit performance. The rms error of the proton chemical shifts is 0.198 ppm, and this can be reduced to 0.140 ppm with scaling. The 6-31G(d) basis set is even better if one uses a linear scaling; its error is only 0.120 ppm. B3LYP/6-31G(d,p) has an rms only somewhat worse. Use of aug-cc-pVTZ basis sets, while substantially more time consuming, provides inferior predictions.

The authors contend that this sort of simple DFT computation, affordable for many organic systems on standard desktop PCs, should be routinely done, especially in preference to increment schemes that are components of some drawing programs. And if a synthesis group does not have the tools to do this sort of work, I’m sure there are many computational chemists that would be happy to collaborate!

References

(1) Jain, R.; Bally, T.; Rablen, P. R., "Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets," J. Org. Chem. 2009, DOI: 10.1021/jo900482q.

(2) Wiitala, K. W.; Hoye, T. R.; Cramer, C. J., "Hybrid Density Functional Methods Empirically Optimized for the Computation of ¹³C and ¹H Chemical Shifts in Chloroform Solution," J. Chem. Theory Comput. 2006, 2, 1085-1092, DOI: 10.1021/ct6001016

Yet more on the benzene dimer. Lesczynski has optimized 9 different benzene dimer configurations, shown in Scheme 1.¹ There are two T-shaped isomers, where a hydrogen from one benzene interacts with the center of the π-cloud of the second. There are two bent versions of the T-shape, called Bent-T-shape. There are two sandwich configurations and two variants where the benzenes are parallel but displaced. Lastly, they report on a new variant, the V-shape configuration. (Once again, the author has not deposited the structures and so I can’t produce interactive figures!)

Scheme 1

The structures were optimized at MP2/aug-cc-pVDZ and then single point energies computed at MP4(SDTQ)/aug-cc-pVDZ and corrected for basis set superposition error. I list these energies in Table 1. They authors note that in comparison with CCSD(T) computations one has to adjust the amount of BSSE correction – which just supports my long-held contention that the standard counterpoise correction overcompensates and that we really have no reliable way of correcting for BSSE.

Table 1. Dimerization energies (kcal mol^-1) at MP4(SDTQ)/aug-cc-pVDZ.¹

The relative energies of the 9 configurations are similar, indicating a very flat potential energy surface. The lowest energy structure is BT-2, and the V-shape configuration is the least favorable of the nine geometries examined.

References

(1) Dinadayalane, T. C.; Leszczynski, J., "Geometries and stabilities of various configurations of benzene dimer: details of novel V-shaped structure revealed " Struct. Chem. 2009, 20, 11-20, DOI: 10.1007/s11224-009-9411-6.

Another two benchmarking studies of the performance of DFT have appeared.

The first is an examination by Csonka and French of the ability of DFT to predict the relative energy of carbohydrate conformation energies.¹ They examined 15 conformers of α- and β-D-allopyranose, fifteen conformations of 3,6-anydro-4-O-methyl-D-galactitol and four conformers of β-D-glucopyranose. The energies were referenced against those obtained at MP2/a-cc-pVTZ(-f)//B3LYP/6-31+G*. (This unusual basis set lacks the f functions on heavy atoms and d and diffuse functions on H.) Among the many comparisons and conclusions are the following: B3LYP is not the best functional for the sugars, in fact all other tested hybrid functional did better, with MO5-2X giving the best results. They suggest the MO5-2X/6-311+G**//MO5-2x/6-31+G* is the preferred model for sugars, except for evaluating the difference between ¹C₄ and ⁴C₁ conformers, where they opt for PBE/6-31+G**.

The second, by Korth and Grimme, describes a “mindless” DFT benchmarking study.²
This is really not a “mindless” study (as the term is used by Schaefer and Schleyer³ and discussed in this post, where all searching is done in a totally automated way) but rather Grimme describes a procedure for removing biases in the test set. Selection of “artificial molecules” is made by first deciding how many atoms are to be present and what will be the distribution of elements. In their two samples, they select systems having 8 atoms. The two sets differ by the distribution of the elements. The first set the atoms Na-Cl are one-third as probable as the elements Li-F, which are one-third as probable as H. The second set has the probability distribution similar to those found in naturally occurring organic compounds. The eight atoms, randomly selected by the computer, are placed in the corners of a cube and allowed to optimize (this is reminiscent of the “mindless” procedure of Schaefer and Schleyer³). This process generates a selection of random bonding environments along with open- and closed shell species, and removes (to a large degree) the biases of previous test sets, which are often skewed towards small molecules, ones where accurate experiments are available or geared towards a select group of molecules of interest. Energies are then computed using a variety of functional and compared to the energy at CCSD(T)/CBS. The bottom line is that the functional nicely group along the rungs defined by Perdew:⁴ LDA is the poorest performer, GGA does much better, the third rung of meta-GGA functionals are slightly better than GGA functionals, hybrids do better still, and the fifth rung functionals (double hybrids) perform quite well. Also of interest is that CCSD(T)/cc-pVDZ gives quite large errors and so Grimme cautions against using this small basis set.

References

(1) Csonka, G. I.; French, A. D.; Johnson, G. P.; Stortz, C. A., "Evaluation of Density Functionals and Basis Sets for Carbohydrates," J. Chem. Theory Comput. 2009, ASAP, DOI: 10.1021/ct8004479.

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, ASAP, DOI: 10.1021/ct800511q.

(3) Bera, P. P.; Sattelmeyer, K. W.; Saunders, M.; Schaefer, H. F.; Schleyer, P. v. R., "Mindless Chemistry," J. Phys. Chem. A 2006, 110, 4287-4290, DOI: 10.1021/jp057107z.

(4) Perdew, J. P.; Ruzsinszky, A.; Tao, J.; Staroverov, V. N.; Scuseria, G. E.; Csonka, G. I., "Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits," J. Chem. Phys. 2005, 123, 062201-9, DOI: 10.1063/1.1904565

One more nail in the coffin of the widely disputed Le Clair structure of hexacyclinol is provided by the B97-2/cc-pVTZ/B3LYP/6-31G(d,p) computed proton and ¹³C NMR for the two “structures” (see my previous blog post for structures and background). These computations¹ are at a more rigorous level than those performed by Rychnovsky, and the addition of the proton spectrum helps clearly settle this issue. Rychnovsky’s structure is the correct one – the mean absolute error between the experimental and computed structure is half that for Rychnovsky structure. The computed coupling constants also are in much better agreement with the Rychnovsky structure. So, Bagno’s contribution accomplishes, I hope, two things: (1) convinces everyone that DFT NMR spectra can be an important tool in identifying natural product structure and (2) closes the book on hexacylinol!

References

(1) Saielli, G.; Bagno, A., "Can Two Molecules Have the Same NMR Spectrum? Hexacyclinol Revisited," Org. Lett. 2009, 11, 1409-1412, DOI: 10.1021/ol900164a.

The failure of DFT in dealing with some seemingly straightforward reactions (as discussed in these previous blog posts: A, B, C, D, E, F) has become a bit clearer. Brittain and co-workers have identified the culprit.¹ They examined twelve different reactions, involving neutral, radical, cations and anions:

R-Me + Me-H → R-H +Me-Me

R-Me + Me^. → R^. + Me-Me

R-Me + Me^– → R^– + Me-Me

R-Me + Me⁺ → R⁺ + Me-Me

where R is ethyl, i-propyl and t-butyl. They used a variety of different functionals, and benchmarked the energies against those found at CCSD(T)/cc-pVTZ. By systematically using different densities and different exchange and correlation components, DFT exchange is responsible for the poor performance – and it can be very poor: the error for the cation reaction with R=t-butyl is 12 kcal mol^-1 with B3LYP and 18 kcal mol^-1 with PBE. It should be noted that the maximum error with G3(MP2) and MP2 is 1.5 and 2.5 kcal mol^-1, respectively. These authors make three important conclusions: (a) that traditional ab initio methods are preferred, (b) that development of new functionals should target the exchange component, and (c) Truhlar’s highly parameterized functional MO5-2X works quite well (maximum error is 2.6 kcal mol^-1 – again for the cation t-butyl case) but the reason for its success is unknown.

References

(1) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys. 2009, DOI: 10.1039/b818412g.