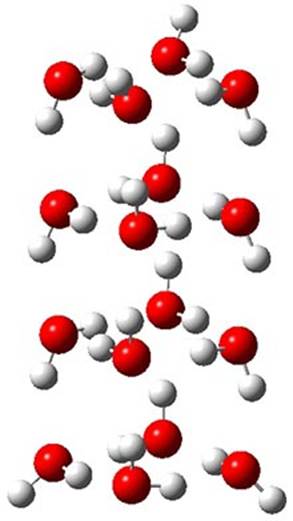
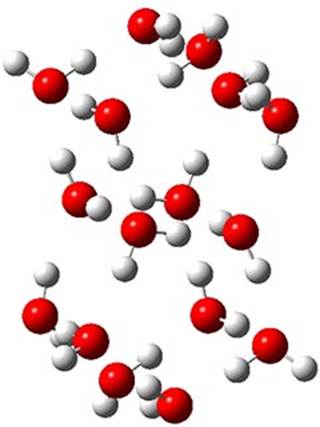
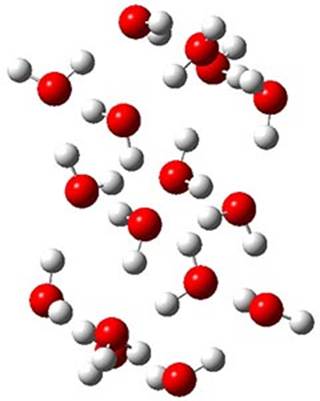
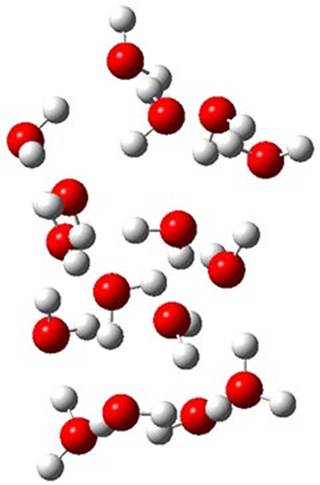
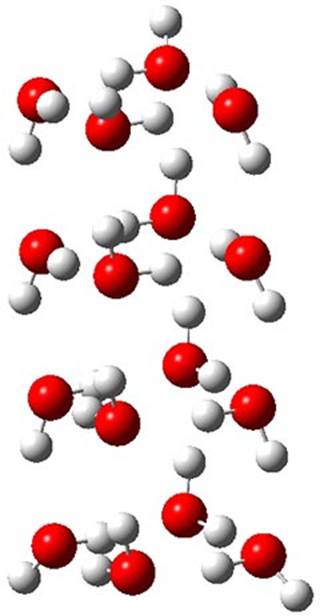
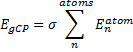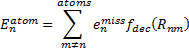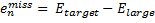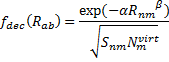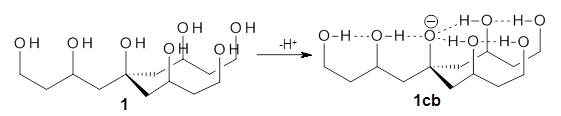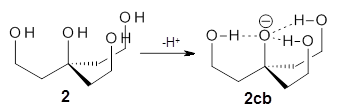Truhlar has made a comparison of binding energies and relative energies of five (H₂O)₁₆ clusters.¹ While technically not organic chemistry, this paper is of interest to the readership of this blog as it compares a very large collection of density functionals on a problem that involves extensive hydrogen bonding, a problem of interest to computational organic chemists.

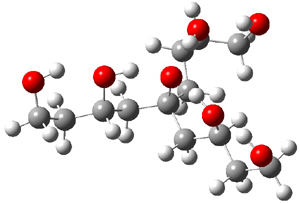
The CCSD(T)/aug-cc-pVTZ//MP2/aug-cc-pVTZ energies of clusters 1-5 (shown in Figure 1) were obtained by Yoo.² These clusters are notable not just for their size but also that they involve multiple water molecules involved in four hydrogen bonds. Truhlar has used these geometries to compute the energies using 73 different density functionals with the jun-cc-pVTZ basis set (see this post for a definition of the ‘jun’ basis sets). Binding energies (relative to 16 isolated water molecules) were computed along with the 10 relative energies amongst the 5 different clusters. Combining the results of both types of energies, Truhlar finds that the best overall performance relative to CCSD(T) is obtained with ωB97X-D, a hybrid GGA method with a dispersion correction. The next two best performing functionals are LC-ωPBE-D3 and M05-2x. The best non-hybrid performance is with revPBE-D3 and B97-D.

1 (0.0)	2 (0.25)
3 (0.42)	4 (0.51)
5 (0.54)

Figure 1. MP2/aug-cc-pVTZ optimized geometries and relative CCSD(T) energies (kcal mol^-1) of (water)₁₆ clusters 1-5. (Don’t forget to click on any of these molecules above to launch Jmol to interactively view the 3-D structure. This feature is true for all molecular structures displayed in all of my blog posts.)

While this study can help guide selection of a functional, two words of caution. First, Truhlar notes that the best performing methods for the five (H₂O)₁₆ clusters do not do a particularly great job in getting the binding and relative energies of water hexamers, suggesting that no single functional really stands out as best. Second, a better study would also involve geometry optimization using that particular functional. Since this was not done, one can garner little here about what method might be best for use in a typical study where a geometry optimization must also be carried out.

References

(1) Leverentz, H. R.; Qi, H. W.; Truhlar, D. G. "Assessing the Accuracy of Density
Functional and Semiempirical Wave Function Methods for Water Nanoparticles: Comparing Binding and Relative Energies of (H₂O)₁₆ and (H₂O)₁₇ to CCSD(T) Results," J. Chem. Theor. Comput. 2013, ASAP, DOI: 10.1021/ct300848z.

(2) Yoo, S.; Aprà, E.; Zeng, X. C.; Xantheas, S. S. "High-Level Ab Initio Electronic Structure Calculations of Water Clusters (H₂O)₁₆ and (H₂O)₁₇: A New Global Minimum for (H₂O)₁₆," J. Phys. Chem. Lett. 2010, 1, 3122-3127, DOI: 10.1021/jz101245s.

Basis set superposition error plagues all practical computations. This error results from the use of incomplete basis sets (thus pretty much all computations will suffer from this problem). The primary example of this error is in the formation of a supermolecule AB from the monomers A and B. Superposition occurs when in the computation of the supermolecule, basis functions centered on B are used to supplement the basis set of A, not to describe the bonding or interaction between the two monomers, but simply to better the description of the monomer A itself. Thus, BSSE always serves to increase the binding in the supermolecule. Recently, this concept has been extended to intramolecular BSSE, as discussed in these posts (A and B).

The counterpoise correction proposed by Boys and Bernardi corrects for the superposition by computing the energy of each monomer using the basis sets centered on both monomers, often referred to as ghost orbitals because the functions are used but not the nuclei upon which they are centered. This can overcorrect for superposition but is the only widely utilized approach to treat the problem. A variation on this approach is what has been suggested for the intramolecular
BBSE problem.

A major discouragement for wider use of counterpoise correction is its computational cost. Kruse and Grimme offer a semi-empirical approach that is extremely cost effective and appears to strongly mimic the traditional counterpoise correction.¹

They define the geometric counterpoise scheme (gCP) that provides an energy correction E_gCP that can be added onto the electronic energy. This term is defined as

Eq. (1)

where σ is an empirically fitted scaling term. The atomic contributions are defined as

where e^miss are the errors in the energy of an atom with a particular target basis set, relative to the energy with some large basis set:

(On a technical matter, the atomic terms are computed in an electric field of 0.6a.u. in order to get some population into higher energy orbitals.) The f_dec term is a decay function that relates to the distance between the atoms (R_nm) and the overlap
(S_nm):

where N^virt is the number of virtual orbitals on atom m, and α and β are fit parameters. Lastly, the overlap term comes from the integral of a single Slater orbital with coefficient

where ξ_s and ξ_p are optimized Slater exponents from extended Huckel theory, and η is the last parameter that needs to be fit.

There are four parameters and these need to be fit for each specific combination of method (functional) and basis set. Kruse and Grimme provide parameters for a number of combinations, and suggest that the parameters devised for B3LYP are suitable for other functionals.

So what is this all good for? They demonstrate that for a broad range of benchmark systems involving weak bonds, the that gCP corrected method coupled with the DFT-D3 dispersion correction provides excellent results, even with B3LYP/6-31G*! This allows one to potentially run a computation on very large systems, like proteins, where large basis sets, like TZP or QZP, would be impossible. In a follow-up paper,² they show that the B3LYP/6-31G*-gCP-D3 computations of a few Diels-Alder reactions and computations of strain energies of fullerenes match up very well with computations performed at significantly higher levels.

Once this gCP method and the D3 correction are fully integrated within popular QM programs, this combined methodology should get some serious attention. Even in the absence of this integration, these energy corrections can be obtained using the web service provided by Grimme at http://www.thch.uni-bonn.de/tc/gcpd3.

References

(1) Kruse, H.; Grimme, S. "A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems," J. Chem. Phys 2012, 136, 154101-154116, DOI: 10.1063/1.3700154

(2) Kruse, H.; Goerigk, L.; Grimme, S. "Why the Standard B3LYP/6-31G* Model Chemistry Should Not Be Used in DFT Calculations of Molecular Thermochemistry: Understanding and Correcting the Problem," J. Org. Chem. 2012, 77, 10824-10834, DOI: 10.1021/jo302156p

This is a short post mainly to bring to the reader’s attention a couple of recent JCTC papers.

The first is a benchmark study by Hujo and Grimme of the geometries produced by DFT computations that are corrected for dispersion.¹ They use the S22 and S66 test sets that span a range of compounds expressing weak interactions. Of particular note is that the B3LYP-D3 method provided the best geometries, suggesting that this much (and justly) maligned functional can be significantly improved with just the simple D3 fix.

The second paper entails the description of Truhlar and Cramer’s latest iteration on their solvation model, namely SM12.² The main change here is the use of Hirshfeld-based charges, which comprise their Charge Model 5 (CM5). The training set used to obtain the needed parameters is much larger than with previous versions and allows for treating a very broad set of solvents. Performance of the model is excellent.

References

(1) Hujo, W.; Grimme, S. "Performance of Non-Local and Atom-Pairwise Dispersion Corrections to DFT for Structural Parameters of Molecules with Noncovalent Interactions," J. Chem. Theor. Comput. 2013, 9, 308-315, DOI: 10.1021/ct300813c

(2) Marenich, A. V.; Cramer, C. J.; Truhlar, D. G. "Generalized Born Solvation Model SM12," J. Chem. Theor. Comput. 2013, 9, 609-620, DOI: 10.1021/ct300900e

Two interesting questions are addressed in a focal-point computational study of t-butyl radical and the t-butyl anion from the Schaefer group.¹ First, is the radical planar? EPR and PES studies from the 1970s indicate a pyramidal structure, with an inversion barrier of only 0.64 kcal mol^-1. The CCSD(T)/cc-pCVTZ optimized structure of t-butyl radical shows it to be pyramidal with the out-of-plane angle formed by one methyl group and the other three carbons of 22.9°, much less than the 54.7° of a perfect tetrahedron. Focal point analysis give the inversion barrier 0.74 kcal mol^-1, in outstanding agreement with experiment.

Second, what is the electron affinity (EA) of the t-butyl radical? Schleyer raised the concern that the alkyl anions may be unbound, and suggested that the electron affinity of t-butyl radical was -9.6 kcal mol^-1; in other words, the anion is thermodynamically unstable. This focal-point study shows just how sensitive the EA is to computational method. The HF/CBS value of the EA is -39.59 kcal mol^-1 (unbound anion), but the MP2/CBS value is +41.57 kcal mol^-1 (bound anion!). The CCSD/aug-cc-pVQZ value is -8.92 while the CCSD(T)/aug-cc-pVQZ value is +4.79 kcal mol^-1. The estimated EA at CCSDT(Q)/CBS is -1.88 kcal mol^-1, and inclusion of correction terms (including ZPE and relativistic effect) gives a final estimate of the EA as -0.48 kcal mol^-1, or a very weakly unbound t-butyl anion. It is somewhat disconcerting that such high-level computations are truly needed for some relatively simple questions about small molecules.

References

(1) Sokolov, A. Y.; Mittal, S.; Simmonett, A. C.; Schaefer, H. F. "Characterization of the t-Butyl Radical and Its Elusive Anion," J. Chem. Theory Comput. 2012, 8, 4323-4329, DOI: 10.1021/ct300753d.

The intramolecular Diels-Alder reaction of 1 occurs slowly, but quantitatively, at room temperature.¹ This is unusual as most Diels-Alder cyclizations require heating to typically 200 °C. For example, the related cyclization of 2 requires heating to 170 °C.² What is the cause for this proximity-induced reaction?

Houk and Baran address this question using a computational approach.³ The Diels-Alder reaction of 2 and a simplified analogue of 1, namely 3, were computed at CPCM/M06-2x/6-311+G(d,p)//B3LYP/6-31G(d). The optimized transition states for the reaction of 2 and 3 are shown in Figure 1. The free energy of activation of 3 is 5.4 kcal mol^-1 lower in energy than the free energy of activation of 2. This is consistent with the much faster reaction of 1 than 2 observed in the experiment.

TS2

TS3

Figure 1. B3LYP/6-31G(d) for the transition states of Reactions 2 and 3.

Partitioning 3 into fragments allows Houk and Baran to apply the distortion model. They find that the rigid diene in 3 (and thereby 1) accelerates the reaction relative to the more flexible diene of 2. Further, strain relief in going from 3 (and thereby 1) to TS3 (and thereby to TS of reaction 1) and the formation of an intramolecular hydrogen bond leads to the lower activation energy of 3, and therefore of 1.

References

(1) Maimone, T. J.; Voica, A.-F.; Baran, P. S. "A Concise Approach to Vinigrol," Angew. Chem. Int. Ed. 2008, 47, 3054-3056, DOI: 10.1002/anie.200800167.

(2) Diedrich, M. K.; Klärner, F.-G.; Beno, B. R.; Houk, K. N.; Senderowitz, H.; Still, W. C. "Experimental Determination of the Activation Parameters and Stereoselectivities of the Intramolecular Diels−Alder Reactions of 1,3,8-Nonatriene, 1,3,9-Decatriene, and 1,3,10-Undecatriene and Transition State Modeling with the Monte Carlo-Jumping Between Wells/Molecular Dynamics Method," J. Am. Chem. Soc. 1997, 119, 10255-10259, DOI: 10.1021/ja9643331.

(3) Krenske, E. H.; Perry, E. W.; Jerome, S. V.; Maimone, T. J.; Baran, P. S.; Houk, K. N. "Why a Proximity-Induced Diels–Alder Reaction Is So Fast," Org. Lett. 2012, 14, 3016-3019, DOI: 10.1021/ol301083q.

InChIs

1: InChI=1S/C23H40O2Si/c1-10-12-19(24)21-20(16(3)4)18-13-14-23(21,15-17(18)11-2)25-26(8,9)22(5,6)7/h10-11,15-16,18-21,24H,1-2,12-14H2,3-9H3/t18?,19-,20?,21?,23+/m0/s1
InChIKey=NGVNTJGCNDZDEY-RHDCMTSYSA-N

2: InChI=1S/C10H16/c1-3-5-7-9-10-8-6-4-2/h3-5,7H,1-2,6,8-10H2/b7-5+
InChIKey=HXZJJSYHNPCGKW-FNORWQNLSA-N

3: InChI=1S/C20H34O2Si/c1-8-10-18(21)20(15(3)4)14-17-11-12-19(20,13-16(17)9-2)22-23(5,6)7/h8-9,13,15,17-18,21H,1-2,10-12,14H2,3-7H3/t17?,18-,19+,20?/m0/s1
InChIKey=GDQHAOHEZAJKPI-FUFFSDJGSA-N

Schreiner has expanded on his previous paper¹ regarding alkanes with very long C-C bonds, which I commented upon in this post. He and his colleagues report² now a series of additional diamond-like and adamantane-like sterically congested alkanes that are stable despite have C-C bonds that are longer that 1.7 Å (such as 1! In addition they examine the structures and rotational barriers using a variety of density functionals.

For 2, the experimental C-C distance is 1.647 Å. A variety of functionals all using the cc-pVDZ basis predict distances that are much too long: B3LYP, B96, B97D, and B3PW91. However, functionals that incorporate some dispersion, either through an explicit dispersion correction (Like B3LYP-D and B2PLYP-D) or with a functional that address mid-range or long range correlation (like M06-2x) or both (like ωB97X-D) all provide very good estimates of this distance.

On the other hand, prediction of the rotational barrier about the central C-C bond of 2 shows different functional performance. The experimental barrier, determined by ¹H and ¹³C NMR is 16.0 ± 1.3 kcal mol^-1. M06-2x, ωB97X-D and B3LYP-D, all of which predict the correct C-C distance, overestimate the barrier by 2.5 to 3.5 kcal mol^-1, outside of the error range. The functionals that do the best in getting the rotational barrier include B96, B97D and PBE1PBE and B3PW91. Experiments and computations of the rotational barriers of the other sterically congested alkanes reveals some interesting dynamics, particularly that partial rotations are possible by crossing lower barrier and interconverting some conformers, but full rotation requires passage over some very high barriers.

In the closing portion of the paper, they discuss the possibility of very long “bonds”. For example, imagine a large diamond-like fragment. Remove a hydrogen atom from an interior position, forming a radical. Bring two of these radicals together, and their computed attraction is 27 kcal mol^-1 despite a separation of the radical centers of more than 4 Å. Is this a “chemical bond”? What else might we want to call it?

A closely related chemical system was the subject of yet another paper³ by Schreiner (this time in collaboration with Grimme) on the hexaphenylethane problem. I missed this paper somehow near
the end of last year, but it is definitely worth taking a look at. (I should point out that this paper was already discussed in a post in the Computational Chemistry Highlights blog, a blog that acts as a journals overlay – and one I participate in as well.)

So, the problem that Grimme and Schreiner³ address is the following: hexaphenylethane 3 is not stable, and 4 is also not stable. The standard argument for their instabilities has been that they are simply too sterically congested about the central C-C bond. However, 5 is stable and its crystal structure has been reported. The central C-C bond length is long: 1.67 Å. But why should 5 exist? It appears to be even more crowded that either 3 or 4. TPSS/TZV(2d,2p) computations on these three compounds indicate that separation into the two radical fragments is very exoergonic. However, when the “D3” dispersion correction is included, 3 and 4 remain unstable relative to their diradical fragments, but 5 is stable by 13.7 kcal mol^-1. In fact, when the dispersion correction is left off of the t-butyl groups, 5 becomes unstable. This is a great example of a compound whose stability rests with dispersion attractions.

3: R₁ = R₂ = H
4: R₁ = tBu, R₂ = H
5: R₁ = H, R₂ = tBu

References

(1) Schreiner, P. R.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Schlecht, S.; Dahl, J. E. P.; Carlson, R. M. K.; Fokin, A. A. "Overcoming lability of extremely long alkane carbon-carbon bonds through dispersion forces," Nature 2011, 477, 308-311, DOI: 10.1038/nature10367

(2) Fokin, A. A.; Chernish, L. V.; Gunchenko, P. A.; Tikhonchuk, E. Y.; Hausmann, H.; Serafin, M.; Dahl, J. E. P.; Carlson, R. M. K.; Schreiner, P. R. "Stable Alkanes Containing Very Long Carbon–Carbon Bonds," J. Am. Chem. Soc., 2012, 134, 13641-13650, DOI: 10.1021/ja302258q

(3) Grimme, S.; Schreiner, P. R. "Steric Crowding Can tabilize a Labile Molecule: Solving the Hexaphenylethane Riddle," Angew. Chem. Int. Ed., 2011, 50, 12639-12642, DOI: 10.1002/anie.201103615

Has there been an organic reaction more examined by computational methods than the Diels-Alder reaction? You’d think we would have covered all aspects of this reaction by now, but no, it appears that this reaction remains fertile hunting grounds.

Doubleday and Houk have examined the Diels-Alder reaction with an eye towards its synchronicity,¹ an area that Houk has delved into throughout his career. While most experiments show significant stereoselectivity, a few examples display a small amount of stereo loss. Computed transition states tend to have forming C-C bond distances that are similar, though with proper asymmetric substitution, the asymmetry of the TS can be substantial. In this paper,¹ they utilize reaction dynamics specifically to assess the time differential between the formation of the two new C-C single bonds. They examined the eight reactions shown below. The first six (R1-R6) have symmetric transition states, though with the random sampling about the TS for the initial condition of the trajectories, a majority of asymmetric starting conditions are used. The last two (R7 and R8) reactions have asymmetric TSs and the random sampling amplifies this asymmetry.

Nonetheless, the results of the dynamics are striking. The time gap, the average time between the formations of the first and second new C-C bond, for R1-R6 is less than 5 fs, much shorter than a C-C vibration. These reactions must be considered as concerted and synchronous. Even the last two reactions (R7 and R8), which are inherently more asymmetric, still have very short time gaps of 15 and 56 fs, respectively. One might therefore reasonably conclude that they too are concerted and synchronous.

There are some exceptions – a few trajectories in the last two reactions involve a long-lived (~1000 fs) diradical intermediate. At very high temperature, about 2% of the trajectories invoke a diradical intermediate. But the overall message is clear: the Diels-Alder reaction is inherently concerted and synchronous.

References

(1) Black, K.; Liu, P.; Xu, L.; Doubleday, C.; Houk, K. N. "Dynamics, transition states, and timing of bond formation in Diels–Alder reactions," Proc. Nat. Acad. Sci. USA, 2012, 109, 12860-12865, DOI: 10.1073/pnas.1209316109

Can a hydrogen bonding network affect acidity? Kass has examined the polyol 1 whose conjugate base 1cb can potentially be stabilized by a large hydrogen bonding network.¹ Kass had previously found a significant acidy enhancement in comparing t-butanol (ΔG(deprotonation) = 369.2 kcal mol^-1) with that of 2 (ΔG(deprotonation) = 334.4 kcal mol^-1).²

Table 1 lists the computed and experimental free energies of deprotonation of 1. The experimental values are computed at M06-2x/maug-cc-pVT(+d)Z. The structure of 1cb is drawn in Figure 1.

Table 1. Computed and experimental free energies (kcal mol^-1 of deprotonation of some alcohols.

The difference in the acidity of t-butanol and 2, some 30 kcal mol^-1, reflects the stability afforded by three intramolecular hydrogen bonds to the oxyanion. In going from 2cb to 1cb, each of the hydroxyl groups that donate to the oxyanion act as the acceptor of a hydrogen bond from the more removed hydroxyl groups. There is in effect a first and second layer of hydrogen bond network in 1cb. These secondary hydrogen bonds lead to further stabilization of the anion, as reflected in the diminished DPE of 1 over 2: 320.2 vs. 335.0 kcal mol^-1. Note that this secondary layer does not stabilize the anion to the same degree as the primary layer, but nonetheless its effect is large and quite striking.

1cb

Figure 1. M06-2x/maug-cc-pVT(+d)Z optimized structure of 1cb.

Even in solution these more remote hydrogen bonds can stabilize the anion. So, using the CPCM approach and modeling DMSO, 2 is predicted have a pK_a that is 15 units below that of t-butanol, and 1 is predicted to be 3 pK_a units more acidic than 2. Experiments verify this prediction with the pK_as of 16.1 for 2 and 11.4 for 1.

References

(1) Shokri, A.; Abedin, A.; Fattahi, A.; Kass, S. R. "Effect of Hydrogen Bonds on pKa Values: Importance of Networking," J. Am. Chem. Soc. 2012, 134, 10646-10650, DOI: 10.1021/ja3037349

(2) Tian, Z.; Fattahi, A.; Lis, L.; Kass, S. R. "Single-Centered Hydrogen-Bonded Enhanced Acidity (SHEA) Acids: A New Class of Brønsted Acids," J. Am. Chem. Soc. 2009, 131, 16984-16988, DOI: 10.1021/ja9075106

InChIs

1: InChI=1S/C13H28O7/c14-4-1-10(17)7-13(20,8-11(18)2-5-15)9-12(19)3-6-16/h10-12,14-20H,1-9H2
InChIKey=HGTVPOTWAYDRSM-UHFFFAOYSA-N

1cb: InChI=1S/C13H27O7/c14-4-1-10(17)7-13(20,8-11(18)2-5-15)9-12(19)3-6-16/h10-12,14-19H,1-9H2/q-1
InChIKey=UQPPTNIHRICITD-UHFFFAOYSA-N

2: InChI=1S/C7H16O4/c8-4-1-7(11,2-5-9)3-6-10/h8-11H,1-6H2
InChIKey=FAQWYKIIWYVDPQ-UHFFFAOYSA-N

2cb: InChI=1S/C7H15O4/c8-4-1-7(11,2-5-9)3-6-10/h8-10H,1-6H2/q-1
InChIKey=WSCPTRIAWKZJFZ-UHFFFAOYSA-N

The activation energy for the 5-endo-dig reaction of the anion 1 is anomalously low compared to its 4-endo-dig and 6-endo-dig analogues. Furthermore, the TS is quite early, earlier than might be expected based on the Hammond Postulate. Alabugin and Schleyer have examined this reaction and found some interesting results.¹

First, NICS(0) values for a series of related intermolecular anionic attack at alkynes show some interesting trends (Table 1). Two of the transition states look like they might be aromatic: the TSs for the 3-exo-dig and the 5-endo-dig reaction have NICS(0) values that are quite negative. However, given the geometry of these TSs, particularly the close proximity of the σ bonds to the ring center, one might be concerned about contamination of these orbitals. So, NICS(0)_MOzz computations, which look at the tensor component perpendicular to the ring using just the π-MOs, shows that the 3-exo-dig is likely non-aromatic (NICS(0)_MOzz is near zero), the TS for the 4-endo-dig reaction is antiaromatic (NICS(0)_MOzz very positive) and the TS for the 5-endo-dig reaction is aromatic (NICS(0)_MOzz is very negative. So this last reaction is the first example of an aromatic transition that is not for a pericyclic reaction!

Table 1. NICS(0) and NICS(0)_MOzz for the TS of some anionic alkyne cyclizations.

These authors argue that the reaction of 1 is an “aborted” sigmatropic shift. A normal pericyclic reaction is a single step with a single (concerted) transition state. An interrupted sigmatropic shift has an intermediate that lies higher in energy than the reactants, such as in the Bergman cyclization of an enediyne. The aborted sigmatropic shift has an intermediate that lies lower in energy than the reactants, such as in the cyclization of 1.

References

(1) Gilmore, K.; Manoharan, M.; Wu, J. I. C.; Schleyer, P. v. R.; Alabugin, I. V. "Aromatic Transition States in Nonpericyclic Reactions: Anionic 5-Endo Cyclizations Are Aborted Sigmatropic Shifts," J. Am. Chem. Soc. 2012, 134, 10584–10594, DOI: 10.1021/ja303341b

I think most organic chemists hold dear to their hearts the notion that selectivity is due to crossing over different transition states. Readers of my book and this blog know of the many examples where this notion simply is not true (see here). This post discusses yet another example taking place in a seemingly simple reaction.

Singleton has examined the nucleophilic substitution reaction of 1 with sodium tolylsulfide.¹ The mono substitution gives potentially two different stereoproducts 2 and 3. The experimental ratio of these products 2:3 is 81:19. (Note that things are a bit more complicated because disubstitution can also occur, but this has been factored into the product ratio.)

Based on previous literature, this reaction is likely to proceed in a concerted fashion, and so one might anticipate running computations to locate a transition state leading to 2 and a transition state leading to 3. In fact, Singleton finds six different TSs (the lowest energy TS 4 is shown in Figure 1), all within 2 kcal mol^-1 of each other at PCM(ethanol)/B3LYP/6-31+G**. However, the intrinsic reaction coordinate going forward from each of these six TSs leads solely to 2; no TS could be located that connects to 3! (Computations were also performed at PCM(ethanol)/M06-2x/6-31+G** which give very similar results.) Classical transition state theory would lead
one to conclude that only 2 should be formed, inconsistent with experiment.

4

5

Figure 1. PCM/B3LYP/6-31+G** optimized structures of TSs 4 and 5.

Furthermore, no intermediate could be located. This is consistent with a concerted mechanism. A second transition state was located which interconverts 2 and 3 with the involvement of a chloride – a sort of addition/rotation/elimination process. This TS 5 is also shown in Figure 1.

A direct dynamics study was performed, and 197 trajectories were computed. Of these, 185 trajectories went to product: 156 to 2 and 29 to 3, for a ratio of 84:16 – in amazing agreement with experiment! The product selectivity is due entirely to dynamic effects. In fact, it is one vibrational mode that dictates the product distribution. Essentially, the nature of the rotation about the C=C bond differentiates the eventual route, with a clockwise rotation leading always to 2 and a counterclockwise rotation leading about a third of the time to 3.

References

(1) Bogle, X. S.; Singleton, D. A. "Dynamic Origin of the Stereoselectivity of a Nucleophilic Substitution Reaction," Org. Lett., 2012, 14, 2528-2531, DOI: 10.1021/ol300817a.

InChIs

1: InChI=1S/C4H4Cl2O/c1-3(7)2-4(5)6/h2H,1H3
InChIKey=NXDUHPYJFYSBCT-UHFFFAOYSA-N

2: InChI=1S/C11H11ClOS/c1-8-3-5-10(6-4-8)14-11(12)7-9(2)13/h3-7H,1-2H3/b11-7-
InChIKey=NCXXSKTZGJETLW-XFFZJAGNSA-N

3: InChI=1S/C11H11ClOS/c1-8-3-5-10(6-4-8)14-11(12)7-9(2)13/h3-7H,1-2H3/b11-7+
InChIKey=NCXXSKTZGJETLW-YRNVUSSQSA-N