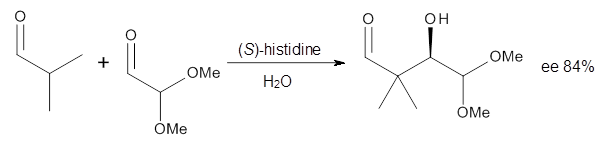
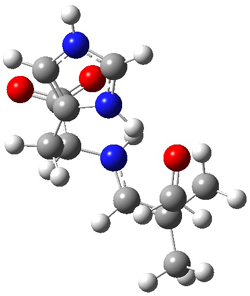
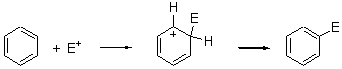
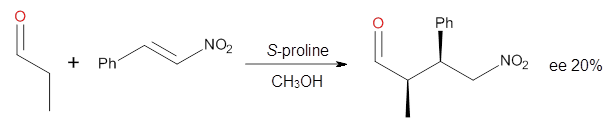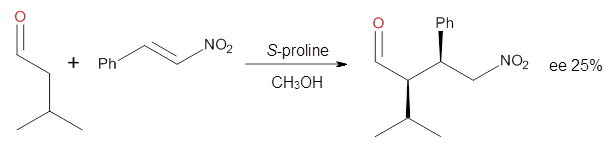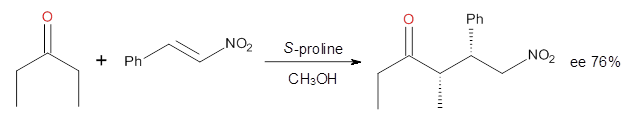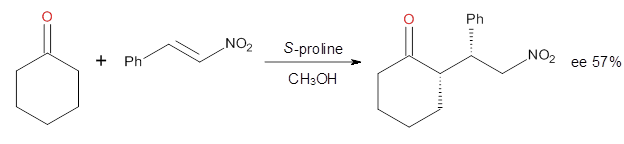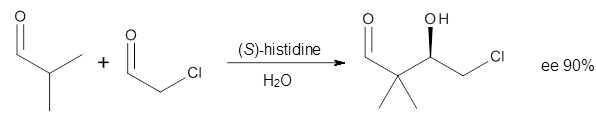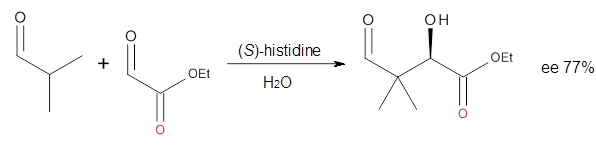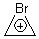Suppose a compound could exist in one of two ways: (a) a symmetrical structure like the bromonium cation A or (b) equilibrating structures that on a time-average basis appear symmetrical, like B. How would one differentiate between these two possibilities?
|
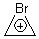
A
|

B
|
Saunders developed a method whereby the species is isotopically labeled and then examined by NMR.1-3 For case B, isotopic labeling will desymmetrize the two structures and so the chemical shifts of what were equivalent nuclei will become (often quite) different. But the isotopic labeling of A, while breaking the symmetry, does so to a much lesser extent, and the chemical shit difference of the (former) equivalent nuclei will be similar.
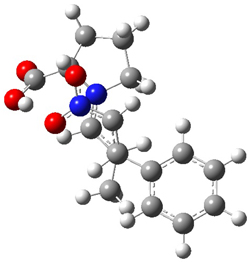
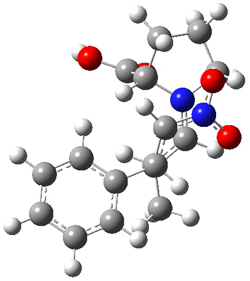
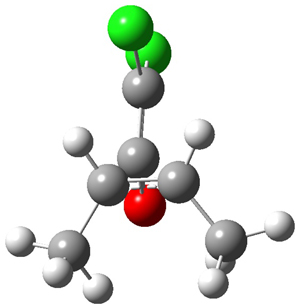
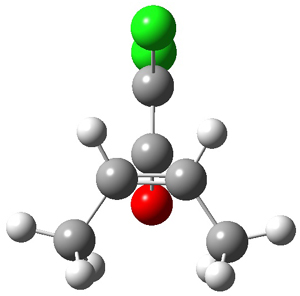
Singelton has employed this concept using both experiment and theory for two interesting cases.4 For the bromonium cation 1, Ohta5 discovered that the 13C NMR chemical shifts differed by 3.61 ppm with the deuterium labels. This led Ohta to conclude that the bomonium cation is really two equilibrating structures. It should be noted that the DFT optimized structure has C2v symmetry (a single symmetric structure). Singleton applied a number of theoretical methods, the most interesting being an MD simulation of the cation. A large number of trajectories were computed and then the NMR shifts were computed at each point along each trajectory to provide a time-averaged difference in the chemical shifts of 4.8 ppm. Thus 2 can express a desymmetrization even though the unlabled structure is symmetric. This desymmetrization is due to coupling of vibrational modes involving the isotopes.
|
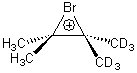
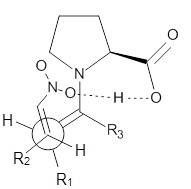
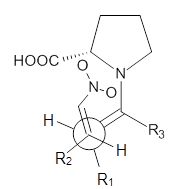
1
|
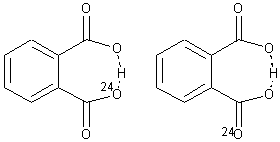
2
|
The second example is phthalate 2. Perrin observed a large 18O chemical shift difference upon isotopic labeling of one of the oxygen atoms, suggesting equilibrating structures.6 An MD study of such a system would take an estimated 1500 processor-years. Instead, by increasing the mass of the label to 24O, the trajectories could be computed in a more reasonable time, and this would result in an isotope effect that is 4 times too large. The oxygen chemical shifts of more the 2.5 million trajectory points were computed for the two labeling cases, and each again showed a large chemical shift difference even though the underlying structure is symmetrical.
Thus, isotopic labeling can desymmetrize a symmetrical potential energy surface.
References
(1) Saunders, M.; Kates, M. R., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance spectra of deuterated cyclohexenyl and cyclopentenyl cations," J. Am. Chem. Soc., 1977, 99, 8071-8072, DOI: 10.1021/ja00466a061
(2) Saunders, M.; Telkowski, L.; Kates, M. R., "Isotopic perturbation of degeneracy. Carbon-13 nuclear magnetic resonance spectra of dimethylcyclopentyl and dimethylnorbornyl cations," J. Am. Chem. Soc., 1977, 99, 8070-8071, DOI: 10.1021/ja00466a060
(3) Saunders, M.; Kates, M. R.; Wiberg, K. B.; Pratt, W., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance of 2-deuterio-2-bicyclo[2.1.1]hexyl cation," J. Am. Chem. Soc., 1977, 99, 8072-8073, DOI: 10.1021/ja00466a062
(4) Bogle, X. S.; Singleton, D. A., "Isotope-Induced Desymmetrization Can Mimic
Isotopic Perturbation of Equilibria. On the Symmetry of Bromonium Ions and Hydrogen Bonds," J. Am. Chem. Soc., 2011, 133, 17172-17175, DOI: 10.1021/ja2084288
(5) Ohta, B. K.; Hough, R. E.; Schubert, J. W., "Evidence for β-Chlorocarbenium and β-Bromocarbenium Ions," Organic Letters, 2007, 9, 2317-2320, DOI: 10.1021/ol070673n
(6) Perrin, C. L., "Symmetry of hydrogen bonds in solution," Pure Appl. Chem., 2009, 81, 571-583, DOI: 10.1351/PAC-CON-08-08-14.