A computational study of addition of singlet carbenes to bicyclobutanes reveals another potential energy surface where dynamics may be active. Rablen, Jones and co-workers examined the reaction of dichlorocarbene with bicyclobutane 1 and 1,2,2-trimethylbicyclobutane 2 (Reactions 1 and 2) using a number of computational techniques.¹

For reaction 1, they identified three reaction pathways. The first two involve the carbene approaching along the central C-C bond. Path A (Scheme 1) involves a single transition state that leads to product 3, with a barrier of 8.4 kcal mol^-1. The second pat (pathway B), leads to critical point 4, which is a transition state at HF/6-31G* and QCISD/6-31G* but is a local minimum at CCSD/6-31G*. This minimum however is very shallow, and vibrational energy will exceed the barriers about it. Both pathways indicate an asynchronous but concerted reaction. The last pathway (C) is for insertion of the carbine into the bridgehead C-C bond, leading to the bicyclo product 5. This barrier is very high, 27 kcal mol^-1, and so this path is unlikely to be competitive.

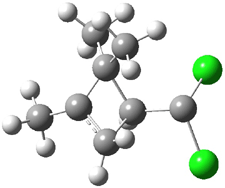
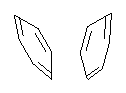
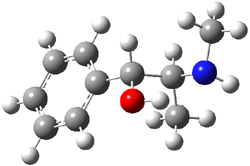
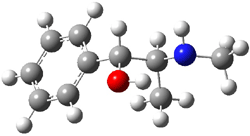
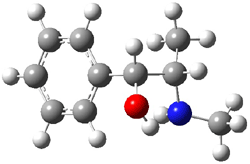
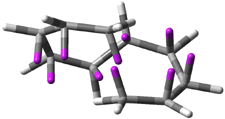
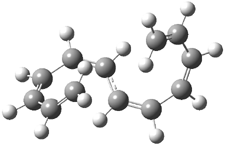
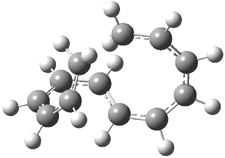
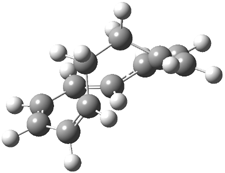
Experimental study of Reaction 2 showed that only 6 is produced.² Rablen and Jones identified six pathways where the carbene attacks 2 along the bridgehead bond (analogous to Paths A and B, except there are three rotamers and the attack can be at either bridgehead carbon) and the insertion path that leads to 8. Once again, this last pathway has a very large barrier and is non-competitive. Attack at the unsubstituted bridgehead carbons is favored over attack at the methyl-substituted bridgehead by 2-3 kcal mol^-1. The path that leads directly to 7 has a slightly lower barrier (0.4 kcal mol^-1) than the path that leads directly to 8. The analog of Path B leads here to a true intermediate 9 through a barrier 0.4 kcal mol^-1 higher than the barrier that leads to 7. This intermediate is shown in Figure 1.

Figure 1. CCSD/6-31G* structure of intermediate 9.¹

The energies of the barriers suggest that 7 will be the major product, but not the exclusive product. Rablen and Jones point out that intermediate 9 lies in a very shallow plateau and exit from this intermediate can lead to either 7 or 8. This sort of potential energy surface has been implicated in reactions that exhibit non-statistical behavior indicative of dynamic effects (see Chapter 7 of my book). Rablen and Jones speculate that dynamics might be dictating the product distribution in Reaction 2 as well. Confirmation awaits a molecular dynamics study.

References

(1) Rablen, P. R.; Paiz, A. A.; Thuronyi, B. W.; Jones, M., "Computational Investigation of the Mechanism of Addition of Singlet Carbenes to Bicyclobutanes," J. Org. Chem. 2009, DOI: 10.1021/jo900485z

(2) Jackson, J. E.; Mock, G. B.; Tetef, M. L.; Zheng, G.-x.; Jones, M., "Reactions of carbenes with bicyclobutanes and quadricyclane : Cycloadditions with two σ bonds," Tetrahedron 1985, 41, 1453-1464, DOI: 10.1016/S0040-4020(01)96386-0.

InChIs

1: InChI=1/C4H6/c1-3-2-4(1)3/h3-4H,1-2H2
InChIKey=LASLVGACQUUOEB-UHFFFAOYAV

2: InChI=1/C7H12/c1-6(2)5-4-7(5,6)3/h5H,4H2,1-3H3
InChIKey=GJMVYBBYZUWWLJ-UHFFFAOYAI

3: InChI=1/C5H6Cl2/c1-2-3-4-5(6)7/h2,4H,1,3H2
InChIKey=FGUOQAVVVDPABB-UHFFFAOYAR

5: InChI=1/C5H6Cl2/c6-5(7)3-1-4(5)2-3/h3-4H,1-2H2
InChIKey=SUZACPSWEYRCBD-UHFFFAOYAW

6: InChI=1/C8H12Cl2/c1-6(2)8(3,4)5-7(9)10/h5H,1H2,2-4H3
InChIKey=QIFFCMZJZYIIBA-UHFFFAOYAZ

7: InChI=1/C8H12Cl2/c1-6(2)7(3)4-5-8(9)10/h5H,4H2,1-3H3
InChIKey=MOELQSRRCNAPQV-UHFFFAOYAX

8: InChI=1/C8H12Cl2/c1-6(2)5-4-7(6,3)8(5,9)10/h5H,4H2,1-3H3
InChIKey=PRCOWYZGJRWGOB-UHFFFAOYAP

Can one steer the course of a reaction by selectively applying a force to a molecule? Atomic force microscopy opens up this avenue. Martinez¹ has just published a computational study on the ring opening of cyclobutene with applied forces. Cyclobutene should ring-open in a conrotatory fashion according to the Woodward-Hoffman rules. But Martinez shows that by pulling on cyclobutene in a cis fashion, the disrotatory pathway can become the more favored route. Thus, it appears that mechanochemistry might be an alternative way to create selectivity in chemical reactions!

References

(1) Ong, M. T.; Leiding, J.; Tao, H.; Virshup, A. M.; Martinez, T. J., “First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene,” J. Am. Chem. Soc., 2009, 131, 6377-6379, DOI: 10.1021/ja8095834.

InChIs

cyclobutene: InChI=1/C4H6/c1-2-4-3-1/h1-2H,3-4H2
InChIKey: CFBGXYDUODCMNS-UHFFFAOYAN

Houk¹ examined the Mannich reaction of the enamine formed from acetone and S-proline with N-ethylidine-N-phenylamine (see Chapter 5.3.3 in my book). Parasuk and Parasuk now extend this to the reaction of the enamine of cyclohexanone and S-proline with N-phenylmethanimine (Reaction 1).² Geometries were optimized at B3LYP/6-31++G(d,p) and single-point energies computed with PCM (for the solvent DMSO) at both B3LYP and MP2.

Reaction 1

First, they examined the formation of the enamine 1, which can be in the syn or anti conformation. The barrier for formation of the syn isomer is 10.2 kcal mol^-1. The barrier for the formation of the anti conformer is much higher, 17.9 kcal mol^-1, and this is with a single water molecule used to assist the proton migration. However, the rotational barrier between the two conformers is only 4.2 kcal mol^-1. So, they conclude that the syn isomer is the only conformer directly formed by the reaction of cyclohexanone and S-proline, and then rotation can produce the anti conformer.

The located the transition state for the reaction of either syn–1 or anti–1 with phenylmethanimine. The two transition states are shown in Figure 1. The barrier for the reaction of syn–1 is 8.5 kcal mol^-1, leading to the S product. The other barrier is higher, 13.0 kcal mol^-1, and the R product 2R is 6.8 kcal mol^-1 higher in energy than the S product 2S. Thus, the reaction to give the S product is both kinetically and thermodynamically favored. This is consistent with experiment³ which gives the S product with 99%ee. Inclusion of solvent makes the S product even more thermodynamically and kinetically favored over the R isomer.

TS-2S

TS-2R

Figure 1. B3LYP/6-311++G(d,p) optimized transition states leading to 2S and 2R.²

References

(1) Bahmanyar, S.; Houk, K. N., "Origins of Opposite Absolute Stereoselectivities in Proline-Catalyzed Direct Mannich and Aldol Reactions," Org. Lett. 2003, 5, 1249-1251, DOI: 10.1021/ol034198e.

(2) Parasuk, W.; Parasuk, V., "Theoretical Investigations on the Stereoselectivity of the Proline Catalyzed Mannich Reaction in DMSO," J. Org. Chem. 2008, 73, 9388-9392, DOI: 10.1021/jo801872w.

(3) Ibrahem, I.; Zou, W.; Casas, J.; Sundén, H.; Córdova, A., "Direct organocatalytic enantioselective α-aminomethylation of ketones," Tetrahedron 2006, 62, 357-364, DOI: 10.1016/j.tet.2005.08.113.

InChIs

1: InChI=1/C11H17NO2/c13-11(14)10-7-4-8-12(10)9-5-2-1-3-6-9/h5,10H,1-4,6-8H2,(H,13,14)/t10-/m0/s1/f/h13
InChIKey=FGOQJKISPWOYSX-WSLRCUSADU

2S: InChI=1/C18H24N2O2/c21-18(22)16-10-6-11-17(16)20-12-5-4-9-15(20)13-19-14-7-2-1-3-8-14/h1-3,7-8,15-16,19H,4-6,9-13H2/b20-17+/t15-,16+/m0/s1
InChIKey=SDMHQUCIHUXJMJ-OQSOEKIEBW

2R: InChI=1/C18H24N2O2/c21-18(22)16-10-6-11-17(16)20-12-5-4-9-15(20)13-19-14-7-2-1-3-8-14/h1-3,7-8,15-16,19H,4-6,9-13H2/b20-17-/t15-,16-/m1/s1
InChIKey=SDMHQUCIHUXJMJ-HGWRPWPUBS

Yet more on the benzene dimer. Lesczynski has optimized 9 different benzene dimer configurations, shown in Scheme 1.¹ There are two T-shaped isomers, where a hydrogen from one benzene interacts with the center of the π-cloud of the second. There are two bent versions of the T-shape, called Bent-T-shape. There are two sandwich configurations and two variants where the benzenes are parallel but displaced. Lastly, they report on a new variant, the V-shape configuration. (Once again, the author has not deposited the structures and so I can’t produce interactive figures!)

Scheme 1

The structures were optimized at MP2/aug-cc-pVDZ and then single point energies computed at MP4(SDTQ)/aug-cc-pVDZ and corrected for basis set superposition error. I list these energies in Table 1. They authors note that in comparison with CCSD(T) computations one has to adjust the amount of BSSE correction – which just supports my long-held contention that the standard counterpoise correction overcompensates and that we really have no reliable way of correcting for BSSE.

Table 1. Dimerization energies (kcal mol^-1) at MP4(SDTQ)/aug-cc-pVDZ.¹

The relative energies of the 9 configurations are similar, indicating a very flat potential energy surface. The lowest energy structure is BT-2, and the V-shape configuration is the least favorable of the nine geometries examined.

References

(1) Dinadayalane, T. C.; Leszczynski, J., "Geometries and stabilities of various configurations of benzene dimer: details of novel V-shaped structure revealed " Struct. Chem. 2009, 20, 11-20, DOI: 10.1007/s11224-009-9411-6.

The Alonso group has once again shown the power of the combination of molecular beam Fourier transform microwave spectroscopy (MB-FTMW) coupled with computations. They examined ephedrine, norephedrine and pseudoephedrine and determined the low energy conformations of each.¹ I discuss just the ephedrine case here, but similar results were obtained for the other two compounds.

1

Ephedrine (1) has six potential conformations, differing by the rotation about the C-C bond and the orientation of the methyl group on the nitrogen. They optimized the 6 conformers at MP2/6-311+G(d,p) and corrected the energies for zero-point vibrational energies computed at B3LYP/6-311++G(d,p). The rotational constants and diagonal elements of the ¹⁴N quadrupole coupling tensor were computed and obtained by experiment. The comparison of these values (shown in Table 1) made possible the identification of three low energy conformers, labeled as AGa, AGb, and GGa. The structures are shown in Figure 1.

Table 1. Experimental and computed^a spectroscopic constants for three conformers of ephedrine.¹

AGa (0.0)	AGb (1.35)
GGa (0.73)

Figure 1. MP2/6-311+G(d,p) computed structures and relative energies (kcal mol^-1) of the three conformers of ephedrine.¹

The agreement between the experimental and computed spectroscopic values is very good, less than 1.5% for the rotational constants. This excellent agreement makes possible the identification of these three conformers. The experimental population ratio of N(AGa):N(GGa):N(AGb) is 20:4:1, in nice agreement with the computed values. Of structural interest here is the intramolecular O-H^…N hydrogen bond in each conformer. The authors also suggest a weak hydrogen bond-like interaction between the N-H and the benzene π-system.

References

(1) Alonso, J. L.; Sanz, M. E.; Lopez, J. C.; Cortijo, V., "Conformational Behavior of Norephedrine, Ephedrine, and Pseudoephedrine," J. Am. Chem. Soc., 2009, 131, 4320-4326, DOI: 10.1021/ja807674q.

InChIs

1: InChI=1/C10H15NO/c1-8(11-2)10(12)9-6-4-3-5-7-9/h3-8,10-12H,1-2H3/t8-,10-/m0/s1
InChIKey=KWGRBVOPPLSCSI-WPRPVWTQBH

The importance of dynamics in simple reactions is made yet again in a recent study by Doubleday and Houk in 1,3-dipolar cycloadditions.¹ They looked at the reaction of acetylene or ethylene with either nitrous oxide, diazonioazanide, or methanediazonium. The transition state for these 6 reactions all show a concerted reaction. The transition vector has three major components; (a) symmetric formation/cleavage of the two new σ bonds, (b) bending of the dipolar component, or (c) symmetric bending of the hydrogens of ethylene or acetylene.

Classical trajectories were traced from the transition state back to reactant and forward to product. In the approach of the two fragments, the dipole bend vibrates, but then after the TS, it needs to bend quickly to close the 5-member ring. This means that the bending mode effectively has to “turn a corner” in phase space, and without energy in this mode, the molecules will simple bounce off of each other. Analysis of the reactants indicates significant vibrational excitation of the dipole bending mode.

References

(1) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloaddition Reactions of Diazonium Betaines to Acetylene and Ethylene: Bending Vibrations Facilitate Reaction," Angew. Chem. Int. Ed. 2009, 48, 2746-2748, DOI: 10.1002/anie.200805906

I blogged on Bickelhaput’s examination of the stability of kinked vs. linear polycyclic aromatics¹ in this post. Bickelhaupt argued against any H^…H stabilization across the bay region, a stabilization that Matta and Bader² argued is present based on the fact that there is a bond path linking the two hydrogens.

Grimme and Erker have now added to this story.³ They prepared the dideuterated phenanthrene 1 and obtained its IR and Raman spectra. The splitting of the symmetric (a₁) and asymmetric (b₁) vibrational frequencies is very small 9-12 cm^-1. The computed splitting are in the same range, with very small variation with the computational methodology employed. The small splitting argues against any significant interaction between the two hydrogen (deuterium) atoms. Further, the sign of the coupling between the two vibrations indicates a repulsive interaction between the two atoms. These authors argue that the vibrational splitting is almost entirely due to conventional weak van der Waals interactions, and that there is no “bond” between the two atoms, despite the fact that a bond path connects them. This bond path results simply from two (electron density) basins forced to butt against each other by the geometry of the molecule as a whole.

References

(1) Poater, J.; Visser, R.; Sola, M.; Bickelhaupt, F. M., "Polycyclic Benzenoids: Why Kinked is More Stable than Straight," J. Org. Chem. 2007, 72, 1134-1142, DOI: 10.1021/jo061637p

(2) Matta, C. F.; Hernández-Trujillo, J.; Tang, T.-H.; Bader, R. F. W., "Hydrogen-Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals," Chem. Eur. J. 2003, 9, 1940-1951, DOI: 10.1002/chem.200204626

(3) Grimme, S.; Mück-Lichtenfeld, C.; Erker, G.; Kehr, G.; Wang, H.; Beckers, H. W., H., "When Do Interacting Atoms Form a Chemical Bond? Spectroscopic Measurements and Theoretical Analyses of Dideuteriophenanthrene," Angew. Chem. Int. Ed. 2009, 48, 2592-2595, DOI: 10.1002/anie.200805751

InChIs

1: InChI=1/C14H10/c1-3-7-13-11(5-1)9-10-12-6-2-4-8-14(12)13/h1-10H/i7D,8D
InChIKey=YNPNZTXNASCQKK-QTQOOCSTEC

Another diversion from the main theme of this blog.

I have been an advocate for a revolution in chemistry publication making use of the technologies available on the net. My latest polemic on this topic is “Chemistry publication – making the revolution” (DOI: 10.1186/1758-2946-1-2) where I advocate for inclusion of more data within articles, enhancing the reader experience by being able to manipulate the data in the same way that the author did. I argue for development of tools that will enable publication of data, along with chemical semantics. Peter Murray-Rust has blogged on perhaps the first step in this direction: Chem4Word.

I ran across a very interesting article on a similar topic in Learned Publishing. The article is “Semantic Publishing: the coming revolution in scientific journal publishing” by David Shotten (DOI: 10.1087/2009202, also available from this repository). Shotten is in the zoology department and so comes to the semantic web with a different perspective, yet arrives at a similar place that I and Peter Murray-Rust and Henry Rzepa (and other chemists) have been advocating. Shotten advocates for “live data” and semantic markup – and cites Project Prospect (the RSC markup of chemical documents built on PMR’s work) as an example of this. Shotten includes a link to a sample zoology article that his group has “enhanced” and there are a lot of clever additions that chemistry publishers would be well served to examine – links to data, cloud tagging, customizable references, etc. Check out the enhanced document here.

Perhaps a growing push for “enhanced publication” from many disciplines will spur on action among the major publishers!

Gronert¹ has published a scathing criticism of the concept of “protobranching” (see my previous blog post) put forth by Schleyer, Houk and Ma² – SHM for short. As a review, protobranching is the term coined by SHM for attractive 1,3-interactions in alkanes. They argue that these attractive 1,3-interactions are the reason for the energetic stability of the branched alkanes over the straight-chain alkanes. Their argument largely rests on the fact that Reaction 1 is exothermic by 2.8 kcal mol^-1.

2 CH₂CH₃ → CH₄ + CH₃CH₂CH₃           Reaction 1

Gronert’s arguments are many and I will discuss only some of them. First, he notes that choosing ethane and methane as the reference molecules leads to all alkanes being stabilized. The stabilization energy of n-heptane is 5.7 kcal mol^-1 and that of n-heptane is 14.1 kcal mol^-1; is this a difference that is meaningful? Under the protobranching method, the stabilization energies of norbornane and n-heptane are quite similar (13.8 and 14.1 kcal mol^-1, respectively) – does that mean they are equally strained? Similarly, protobranching leads to an extraordinary prediction for the resonance energy of benzene: 69 kcal mol^-1. (I find these arguments quite compelling – the use of protobranching extenuates to magnitude of many chemical effects like ring strain, π-conjugation and resonance energy to the point that they become unusable.)

Gronert notes that the C-C-C angle in propane is larger than 109.5°, suggestive of a repulsive force, and one that is in fact much larger than suggested by SHM. The “attractive interaction” is not reproduced in intermolecular models. He points out the SHM attribute the attractive 1,3-interaction in alkenes to hyperconjugation and not to protobranching, and further notes that SHM correct for the strength of the C-H bond in ethyne but not for the C_sp-C bond in propyne, nor do they make any such corrections for the alkenes.

But Gronert’s main complaint rests on the fact that there is simply no evidence for an attractive 1,3-interaction. All previous suggestions for this have been refuted by many others over the past 30 years. SHM’s main support rests on the ability to fit the thermodynamic trends, but Gronert points out that many other possibilities exist for doing so, including a repulsive model. There is ample evidence to support a repulsive interaction. It seems to me that Schleyer, Houk and Ma have their work cut out for them to carefully rebut Gronert’s arguments.

References

(1) Gronert, S., "The Folly of Protobranching: Turning Repulsive Interactions into Attractive Ones and Rewriting the Strain/Stabilization Energies of Organic Chemistry," Chem. Eur. J. 2009, DOI: 10.1002/chem.200800282

(2) Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K. N.; Schleyer, P. v. R., "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations," Chem. Eur. J. 2007, 13, 7731-7744, DOI: 10.1002/chem.200700602

Careful consideration of orbital topolologies of pericyclic reactions has led to the recent flurry of activity related to Möbius aromaticity, homoaromaticity, and antiaromaticity. I discussed this briefly in Chapter 2 of the book and in these posts (1, 2, 3). Mauksh and Tsogoeva¹ have clearly demoted the four different topologies of the transition state of pericyclic reactions. One need to be concerned about (a) the topology of the molecule (does it will have the familiar twist of a Möbius strip or not?) and (b) the topology of the π-system (is there a phase inversion or not?). These four topologies are shown in Figure 1. The pink stick represents the positive lobe of the carbon p orbital.

(A)	(B)
(C)	(D)

Figure 1. Topologies of electrocyclization reactions.

Three of these possibilities had been previously identified. The first (Fig. 1A) is the TS for the electrocyclization of 1,3,5-hexadiene. It has both Hückel topology of the molecule and the p orbitals. The second example (Fig. 1B) is the classic Zimmerman example of the electrocyclization of all-cis 1,3,5,7-octatetraene. It has Hückel topology of the molecule but one phase inversion of the p orbitals. The third example (Fig 1C) is the electrocyclization of (3E,5Z,7E)-1,3,5,7,9-decapentaene, proposed by Rzepa.² Here we have a Möbius topology but there is no phase inversion of the p orbitals.

Mauksch and Tsogoeva report on the novel electrocylization of (3E,5E,7E,9E)-1,3,5,7,9,11-dodecahexaene (1), the fourth topology type (Fig 1d).¹ Here the molecule has the Möbius topology and there is one phase inversion. Figure 2 displays the geometries of the reactant 1, the electrocyclization transition state 2, and the product 3. The activation barrier is 35.7 kcal mol^-1. The NICS value at the center of the ring of the transition state is -12.8ppm , indicative of aromatic character, which is supported by the very small variation of the C-C distances (less than 0.02 Å).

1

2

3

Figure 2. B3LYP/6-31G* optimized geometries of 1-3.¹

Henry Rzepa has commented on this paper in his blog, along with detailing another example of this type of topology. In a second post, Henry discusses the issue of competition between aromatic and antiaromatic character in a related molecule.

References

(1) Mauksch, M.; Tsogoeva, S. B., "A Preferred Disrotatory 4n Electron Möbius Aromatic Transition State for a Thermal Electrocyclic Reaction," Angew. Chem. Int. Ed., 2009, 48, 2959-2963, DOI: 10.1002/anie.200806009

(2) Rzepa, H. S., "Double-twist Möbius aromaticity in a 4n+2 electron electrocyclic reaction," Chem. Commun., 2005, 5220-5222, DOI: 10.1039/b510508k.

InChIs

(3Z)-1,3,5-hexatriene: InChI=1/C6H8/c1-3-5-6-4-2/h3-6H,1-2H2/b6-5-
InChIKey=AFVDZBIIBXWASR-WAYWQWQTBR

(3Z,5Z)-octa-1,3,5,7-tetraene: InChI=1/C8H10/c1-3-5-7-8-6-4-2/h3-8H,1-2H2/b7-5-,8-6-
InChIKey=VXQUABLSXKFKLO-SFECMWDFBK

(3Z,5E,7Z)- 1,3,5,7,9-decapentaene: InChI=1/C10H12/c1-3-5-7-9-10-8-6-4-2/h3-10H,1-2H2/b7-5-,8-6-,10-9+
InChIKey=XKWRJEBRBGIQBA-LODOGNSSBI

(3Z,5Z,7Z,9Z)- 1,3,5,7,9,11-dodecahexaene (1): InChI=1/C12H14/c1-3-5-7-9-11-12-10-8-6-4-2/h3-12H,1-2H2/b7-5-,8-6-,11-9-,12-10-
InChIKey=GLCGEJFIZRSXBL-CAVFYFSLBM

(1Z,3Z,5E,7Z,9Z)-cyclododeca-1,3,5,7,9-pentaene (3): InChI=1/C12H14/c1-2-4-6-8-10-12-11-9-7-5-3-1/h1-10H,11-12H2/b2-1+,5-3-,6-4-,9-7-,10-8-
InChIKey=DULJMQFBRDFTQN-UWFJMCQMBK