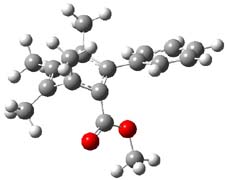
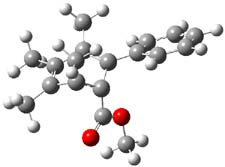
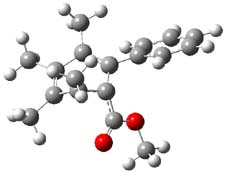
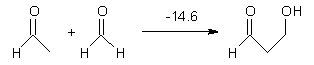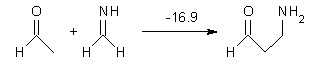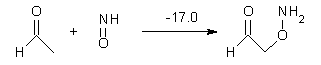Houk has performed a very nice examination of the performance of some density functionals.¹ He takes a quite different approach than what was proposed by Grimme – the “mindless” benchmarking² using random molecules (see this post). Rather, Houk examined a series of simple aldol, Mannich and α-aminoxylation reactions, comparing their reaction energies predicted with DFT against that predicted with CBQ-QB3. The idea here is to benchmark DFT performance for simple reactions of specific interest to organic chemists. These reactions are of notable current interest due their involvement in organocatalytic enantioselective chemistry (see my posts on the aldol, Mannich, and Hajos-Parrish-Eder-Sauer-Wiechert reaction). Examples of the reactions studied (along with their enthalpies at CBS-QB3) are Reaction 1-3.

For the four simple aldol reactions and four simple Mannich reactions, PBE1PBE,
mPW1PW91 and MO6-2X all provided reaction enthalpies with errors of about 2 kcal mol^-1. The much maligned B3LYP functional, along with B3PW91 and B1B95 gave energies with significant larger errors. For the three α-aminoxylation reactions, the errors were better with B3PW91 and B1B95 than with PBE1PBE or MO6-2X. Once again, it appears that one is faced with finding the right functional for the reaction under consideration!

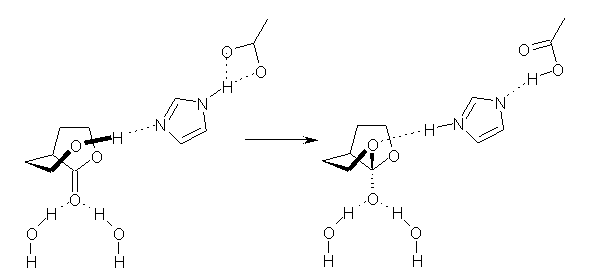
Of particular interest is the decomposition of these reactions into related isogyric, isodesmic
and homdesmic reactions. So for example Reaction 1 can be decomposed into Reactions 4-7 as shown in Scheme 1. (The careful reader might note that these decomposition reactions are isodesmic and homodesmotic and hyperhomodesmotic reactions.) The errors for Reactions 4-7 are typically greater than 4 kcal mol^-1 using B3LYP or B3PW91, and even with MO6-2X the errors are about 2 kcal mol^-1.

Scheme 1.

Houk also points out that Reactions 4, 8 and 9 (Scheme 2) focus on having similar bond changes as in Reactions 1-3. And it’s here that the results are most disappointing. The errors produced by all of the functionals for Reactions 4,8 and 9 are typically greater than 2 kcal mol^-1, and even MO2-6x can be in error by as much as 5 kcal mol^-1. It appears that the reasonable performance of the density functionals for the “real world” aldol and Mannich reactions relies on fortuitous cancellation of errors in the underlying reactions. Houk calls for the development of new functionals designed to deal with fundamental simple bond changing reactions, like the ones in Scheme 2.

Scheme 2

References

(1) Wheeler, S. E.; Moran, A.; Pieniazek, S. N.; Houk, K. N., "Accurate Reaction Enthalpies and Sources of Error in DFT Thermochemistry for Aldol, Mannich, and α-Aminoxylation Reactions," J. Phys. Chem. A 2009, 113, 10376-10384, DOI: 10.1021/jp9058565

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, 5, 993–1003, DOI: 10.1021/ct800511q

Dewar benzene has fascinated physical organic chemists for a long time. Just how does this open up? And why is is stable, given its large strain and the aromaticity of the ring-opened product? Most had rationalized this by recognizing that the route that takes Dewar benzene into benzene is the symmetry-forbidden disrotatory path, and the symmetry allowed conrotatory path leads to the benzene with a trans double bond.

Johnson¹ discovered that the conrotatory TS is high in energy, but below the C_2v structure thought to be the disrotatory TS, but is in fact a saddle point. Further, the IRC path through the conrotatory TS connects Dewar benzene to benzene, avoiding the trans-benzene (which is sometimes referred to as Möbius benzene).

Now comes a report that the PES for opening of Dewar benzene is a bit more complicated.² B3LYP/6-311+G** computations of 1 going to 3 identifies not only the Möat;bius benzene intermediate 2 but a transition state connecting 1 to 2 and a second transition state that connects 2 with 3. These structures are shown in Figure 1.

1	TS1
2	TS2
3

Figure 1. B3LYP/6-311+G** optimized geometries of 1-3 and the two TSs.²

The first TS is 31.0 kcal mol^-1 above reactant and the Möbius benzene intermediate is only 2.1 kcal mol^-1 below this TS. The second TS is 1.6 kcal mol^-1 higher than the first TS, and so is rate-limiting.

The authors also examined a series of related Dewar benzenes and all have two TSs, with the second always higher than the first.

Molecular dynamics computations suggest that the Möbius benzene is likely avoided during the reaction. The fact that the two TSs are similar in energy disguised the fact that there is a second one – the energy of the first TS matches up nicely with experiments. Further MD studies would be interesting to see the interplay between the geometrically quite close intermediate and two TSs – some novel dynamics might be at work here.

References

(1) Johnson, R. P.; Daoust, K. J., "Electrocyclic Ring Opening Modes of Dewar Benzenes: Ab Initio Predictions for Möbius Benzene and trans-Dewar Benzene as New C₆H₆ Isomers," J. Am. Chem. Soc., 1996, 118, 7381-7385, DOI: 10.1021/ja961066q

(2) Dracinsky, M.; Castano, O.; Kotora, M.; Bour, P., "Rearrangement of Dewar Benzene Derivatives Studied by DFT," J. Org. Chem. 2010, ASAP, DOI: 10.1021/jo902065n

InChIs

1: InChI=1/C18H20O2/c1-11-12(2)18(4)15(16(19)20-5)14(17(11,18)3)13-9-7-6-8-10-13/h6-10H,1-5H3
InChIKey=LGAXKHBTTKUURV-UHFFFAOYAH

3: InChI=1/C18H20O2/c1-11-12(2)14(4)17(18(19)20-5)16(13(11)3)15-9-7-6-8-10-15/h6-10H,1-5H3
InChIKey=OUPUSCZNPIJJAH-UHFFFAOYAO

Stoyanov and Reed¹ have reported the IR spectrum of strong acid in water, trying to identify the true nature of the hydrated proton. In other words, what is n in the formula H(H₂O)_n⁺? The key to addressing this problem is to carefully measure the IR spectrum and then remove the signals due to (a) water associated with (or perturbed by) the anion and (b) bulk water. Simply subtracting out bulk water overcorrects because some waters are associated with the proton. By properly scaling the bulk water peak, they identify n as six. Deconvolution of the spectrum of H(H₂O)₆⁺ gives peaks at 3134 ±12, 2816 ± 40, 1746 ± 11, 1202 ± 4 and 654 ± 12 cm^-1.

They suggest that the hydrated proton has structure 3, which is distinguished from previous proposals of H(H₂O)₄⁺ 2 and H(H₂O)₂⁺ 1.

Somewhat surprising is that these authors did not compute the structures of these ions and their IR spectrum. So just to motivate further work I have computed the spectrum of the three ions at PBE1PBE/6-311++G(2df,p)//PBE1PBE/6-31+G(d,p) (Figure 1) and their uncorrected IR frequencies within the range 500-3000 cm^-1 (and intensities greater than 50) are listed in Table 1.

1

2

3

Figure 1. PBE1PBE/6-31+G(d,p) structures of 1 and 3 and PBE1PBE/6-311++G(2df,p) of 2.

Table 1. Computed frequencies (cm^-1) and intensities of 1-3.

The comparison between experiment and computation leaves something to be desired and more careful computation is clearly warranted. In addition, these types of complexes are likely to be dynamic, and so multiple different configurations and conformations will need to be sampled. So, again to promote contributions to this problem, I offer three other configurations of H(H₂O)₆⁺, shown in Figure 2. Their computed IR frequencies are listed in Table 2. Any additional interested takers?

3b -0.48 (0.60)

3c 3.41 (4.80)

3d -1.33 (1.33)

Figure 2. PBE1PBE/6-31+G(d,p) structures of 3b-3d along with their relative (to 3) electronic energy (kcal mol^-1 and electronic energy with ZPE (in parenthesis).

Table 2. Computed frequencies and intensities of 3b-3d.

References

(1) Stoyanov, E. S.; Stoyanova, I. V.; Reed, C. A., "The Structure of the Hydrogen Ion (H_aq⁺) in Water," J. Am. Chem. Soc., 2010, 132, 1484-1485, DOI: 10.1021/ja9101826

Predicting the pK_a of a compound from first principles remains a challenge, despite all of the many algorithmic and methodological advantages within the sphere of computational chemistry. Predicting the gas-phase deprotonation energy is relatively straightforward as I detail in Section 2.2 of my book. The difficulty is in treating the solvent and the interaction of the acid and its conjugate base in solution. Considering that we are most interested in acidities in water, a very polar solvent, the interactions between water and the conjugate base and the proton are likely to be large and important!

Baker and Pulay report a procedure for determining acidities with the aim of high throughput.¹ Thus, computational efficiency is a primary goal. Their approach is to compute the enthalpy change for deprotonation in solution using a continuum treatment and then employ a linear fit to predict the pK_a with the equation:

pK_a(c) = α_cΔH + β_c

where c designates a class of compound, such as alcohol, carboxylic acid, amine, etc. Fitting constants α_c and β_c need to be found then for each unique class of compound, where the fitting is to experimental pK_as in water. In their test suite, they employed eleven anilines and amines, seven pyridines, nine alcohols and phenols, and seven carboxylic acids.

They test a number of different computational variants: (a) what functional to employ, (b) what basis set to use for optimizing structures, and (c) what basis set to use for the enthalpy computation. They opt to employ COSMO for treating the solvent and quickly reject the use of gas phase structures (and particularly use of geometries obtained with molecular mechanics. Their ultimate model is OLYP/6-311+G**//3-21G(d) with the COSMO solvation model. Mean deviation is less than 0.4 pK units. They do note that use of HF or PW91 provides similar small errors, but ultimately favor OLYP for its computational performance.

While this procedure offers some guidance for future computation of acidity, I find a couple of issues. First, it relies on fitted parameters for every class of compound. If one is interested in a new class, then one must develop the appropriate parameters – and the experimental values may not be available or perhaps an insufficient number of them are experimentally available. Second, the parameters cover-up a great deal of problematic computational sins, like the solvation energy of the proton, small basis sets, missing correlation energies, missing dispersion corrections etc. A purist might hope for a computational algorithm that allows for systematic correction and improvement in the estimation of pK_as. Further work needs to be done to meet this higher goal.

References

(1) Zhang, S.; Baker, J.; Pulay, P., "A Reliable and Efficient First Principles-Based Method for Predicting pKa Values. 1. Methodology," J. Phys. Chem. A 2010, 114 , 425-431, DOI: 10.1021/jp9067069

The recent synthesis and characterization of the quadrannulene 1 once again stretches
our notions of aromaticity.¹

The core of this system is a four-member ring with four fused-phenyl rings, forming the very small circulene (see this earlier post on circulenes). One might write other resonance structures for the molecule, which could include a central cyclobutadienyl fragment. However, the X-ray structure and computational analysis rejects any significant contribution of the cyclobutadienyl character. First, the four C-C bond of this central ring are 1.45 Å long, with an NBO bond order of 1.08, signifying single bonds. The bonds from the central 4-member ring are 1.36 Å long with bond order of 1.77 – these are double bonds. NICS computations attest to the central ring (+4.5 ppm) being more like [4]radialene (with a NICS value of -2.6 ppm) than like cyclobutadiene (with a NICS value of +16.5 ppm). The 6-member rings fused to the central ring have NICS values of -2.33 ppm, suggesting a non aromatic character, while the outer rings have NICS values of -10.7ppm, similar to that of benzene. The structure is clearly of radialene form. Nonetheless, the central ring possess extremely pyramidalized carbons, as seen in Figure 1, and their π-orbital axis vector, a measure of the pyramidalization, is 107°, which is similar to the idealized tetrahedral value of 109.47°. Despite this stain, the molecule is thermally stable to 170°C and reacts only slowly with air or base. This molecule will surely inspire further work in the small circulenes.

1

1a

Fig 1. B3LYP/6-311G** structures of 1 and its parent 1a (lacking the TMS groups).¹

References

(1) Bharat, R. B.; Bally, T.; Valente, A.; Cyranski, M. K.; Dobrzycki, L.; Spain, S. M.; Rempala, P.; Chin, M. R.; King, B. T., "Quadrannulene: A Nonclassical Fullerene Fragment," Angew. Chem. Int. Ed. 2009, DOI: 10.1002/anie.200905633

InChIs

1: InChI=1/C44H48Si4/c1-45(2,3)33-21-29-30(22-34(33)46(4,5)6)38-27-19-15-16-20-28(27)40-32-24-36(48(10,11)12)35(47(7,8)9)23-31(32)39-26-18-14-13-17-25(26)37(29)41-42(38)44(40)43(39)41/h13-24H,1-12H3
InChIKey=CDVRNAINHDQBCN-UHFFFAOYAM

1a: InChI=1/C32H16/c1-2-10-18-17(9-1)25-19-11-3-4-12-20(19)27-23-15-7-8-16-24(23)28-22-14-6-5-13-21(22)26(18)30-29(25)31(27)32(28)30/h1-16H
InChIKey=QTVPEOVCCYEZNL-UHFFFAOYAK

The conformational preference of α-β-unsaturated carbonyl compounds is well established: the two π-bonds prefer to be in conjugation with the oxygen and three carbon atoms (nearly) coplanar. Now, what about the conformational preference of vinyl sulfoxides? Since the S-O π-bond is weak, alternate conformations might be favorable. Podlech has prepared some 1,3-dithian-1-oxides that should be conformationally static and thereby offer some insight into this question.¹ The dithiane oxides 1 and 2 can exist with the S-O bond in the axial (a) or equatorial (e) positions.

The B3LYP/6-31++G(d,p) geometries are shown in Figure 1. The equatorial structure has the two π bonds close to coplanar (the C-C-S-O dihedral is 14°), while in the axial isomers, the C-C-S-O dihedral is about -122°.

1a	1e
2a	2e

Figure 1. B3LYP/6-31++G(d,p) optimized structures of 1 and 2.

Podlech argues for a π_C=C → σ*_S-O stabilization in the axial isomer on the basis of two observations. First, the UV maximum absorbance in 1a is at 266nm, 12 nm greater than in 1e and similarly, the UV maximum in 2a is 2 nm higher than in 2e. Second, NBO analysis indicates a much larger contribution for this interaction in 1a (3.05 kcal mol^-1) than in 1e (0.07 kcal mol^-1).

However, I am unconvinced that this interaction is really dominant. Oxidation of the precursor dithiane with MCPBA gives a 42:58 ratio of 1e:1a and a 76:24 ratio of 2e:2a, which indicates a preference for the equatorial form of 1 and only a small preference for the axial form of 2. Unreported by Podlech (even in the supporting materials) is the relative computed energy difference of the two stereoisomers. At B3LYP/6-31++G(d,p) with ZPE, 1e is 2.6 kcal mol^-1 lower in energy than 1a and 2e is 0.05 kcal mol^-1 lower than 2a. So, in the gas-phase, it appears that the vinyl sulfoxides prefer the equatorial orientation, just as in α-β-unsaturated carbonyl compounds. The π_C=C → σ*_S-O interaction is stronger in the axial conformation, but it is doubtful that this alone manifests in any diastereomeric selectivity.

References

(1) Ulshöfer, R.; Podlech, J., "Stereoelectronic Effects in Vinyl Sulfoxides," J. Am. Chem. Soc. 2009, 131, 16618-16619, DOI: 10.1021/ja904354g

The standard model for explaining enzyme activation is that the active site is designed to stabilize the transition state, thereby reducing the activation barrier. Jonathan Goodman offers a very compelling argument for an alternative explanation for at least some enzymes.¹

He examined enzymes that coordinate the substrate through what’s called an “oxyanion hole”, a region in the active site where an incipient oxyanion can be stabilized through 2 or three hydrogen bonds. This usually involves nucleophilic attack at a carbonyl. Analysis of the protein data bank turned up several hundred such structures where a carbonyl is coordinated to the enzyme by 2 or more hydrogen bonds. Also examined were several hundred small molecule x-ray structures that also exhibit this sort of hydrogen bonding scheme. The geometry about the carbonyl oxygen was examined – distances angles and dihedral angles – and the only significant difference between the enzyme and small molecule set is for the dihedral angle formed between the O=C-R plane of the carbonyl and the C=O^…H angle to the hydrogen bond donor. For the small molecules, the preferred value is about 0°, but for the enzymes, the preferred angle is about 90°.

MPWB1K/6-311++G**//B3LYP/6-31G(d,p) computations of a model enzyme active site (see Scheme 1) were performed where the two waters are arranged at different dihedral angles. For both reactant and transition state, the coordinating waters stabilize the structures – and there is a stabilization for all dihedral angles.

Scheme 1

But the best arrangement, i.e. the maximum stabilization, occurs when the waters are arranged with a dihedral angle of 0° for both the reactant and transition state. At 0°, the reactant is significantly stabilized, more so than the stabilization of the TS. At 90° stabilization of both species is less than at 0° but the stabilization is much less for the reactant than for the TS. Thus, at 90° the activation barrier is lowered not by preferential stabilization of the TS but by lesser stabilization of the reactant! The active site is set up not to stabilize the TS but rather to minimize the activation barrier through differential stabilization of the reactant vs the TS. This new model offer another approach towards creating artificial catalysts, ones designed not to maximize binging, but rather to minimize the activation barrier through judicious stabilization of the TS and destabilization of the reactant.

References

(1) Simon, L.; Goodman, J. M., "Enzyme Catalysis by Hydrogen Bonds: The Balance between Transition State Binding and Substrate Binding in Oxyanion Holes," J. Org. Chem. 2010, DOI: 10.1021/jo901503d

Hard to believe but here’s another approach to dealing with intramolecular basis set super position error (BSSE). (I blogged on a previous approach here.) Jensen’s approach¹ is to define the atomic counterpoise correction as

ΔE_ACP = Σ E_A(basisSet_A) – E_A(basisSet_AS)

where this sum runs over all atoms in the molecule and E_A(basisSet_A) is the energy of atom A using the basis set centered on atom A. The key definition is of the last term E_A(basisSet_AS), where this is the energy of atom A using the basis set consisting of those function centered on atom A and some subset of the basis functions centered on the other atoms in the molecule. The key assumption then is just how to select the subset of ghost functions to include in the calculation of the second term.

For intermolecular basis set superposition error, Jensen suggests using the orbitals on atom A along with all orbitals on the other fragment, but not include the orbitals on other atoms in the same fragment where atom A resides. He demonstrates that this approach gives essentially identical superposition corrections as the traditional counterpoise correction for N₂, ethylene dimer and benzene dimer.

For intramolecular corrections, Jensen suggests keeping only the orbitals on atoms a certain bonded distance away from atom A. So for example, ACP(4) would indicate that the energy correction is made using all orbitals on atoms that are 4 or more bonds away from atom A. Jensen suggests in addition that orbitals on atoms that are farther than some cut-off distance away from atom A may also be omitted. He demonstrates the use of these ideas for the relative energies of tripeptide conformational energies.

So while the ACP method is conceptually simple, and also computationally efficient, it does require some playing around with the assumptions of which orbitals will comprise the appropriate subset. And it may be that one has to tune this selection for the individual system of interest.

References

(1) Jensen, F., "An Atomic Counterpoise Method for Estimating Inter- and Intramolecular Basis Set Superposition Errors," J. Chem. Theory Comput. 2010, 6, 100–106, DOI: 10.1021/ct900436f.

I have recently finished reading Free: The Future of a Radical Price by Chris Anderson (buy it here). The premise of the book is that giving things away is not only a serious business plan, it might just be the only business plan for the new economy. I found the book interesting, but ultimately disappointing. All of the models that are in practice or ones he proposes rest upon analogy to the old Gillette razor blade model: give away the razor and sell the blades. The perhaps most successful modern example is giving away search services and browsers and email services all supported by ad placement (Google). Perhaps less successful universally, but certainly working for some, are those bands who give away songs and albums, hoping it leads to concert visits where fans will not just buy tickets but also t-shirts and other paraphernalia.

Giving away stuff is a nice idea, and in the field of science, particularly computational science, we have lots of examples, like free operating systems, free technical software, and free databases. But in reality they’re not truly free.

The problem ultimately is that money needs to be made somewhere; people got to eat and put a roof over their heads and get clothes and that requires real cash. So virtually all of the people developing the computational tools are being paid in some other way – say off of an NSF grant, or by the university or by their commercial employer. Or one produces some code in the hope that it attracts attention that can lead to real paying employment; one might think of this as “reputation payment” that might sometime soon be cashed in for real currency!

Now some stuff, and that can include valuable stuff, is produced truly for free. A great example are the thousands of people who contribute to Wikipedia in their free time. Those chemists who have volunteered to clean up wikipedia entries have done a great job (like this one on the recently infamous PETN) and they not only don’t get paid, they largely contribute anonymously – so they don’t even get a “reputation payment”. The same goes for the many contributors to ChemSpider. But this work is done piecemeal and infrequently and must by definition be a personal low priority because of the need to do work that puts cash in hand.

So, that leads me to ask the question “why Blog? especially why blog in chemistry?” Not an easy one to really figure out, because unless one is just doing it on a lark or very infrequently, the time necessary to blog in a serious way is quite an investment. One has to figure out how to make the blog pay off in some way. Given that our community has not adopted blogging as a means for publishing original research, though Henry Rzepa is attempting to push on this course of action (see his blog), blogging must serve some other purpose, and one that can either directly pay cash or directly raise one’s reputation.

So I’ll answer the question for myself. I blog not for altruistic reasons. While I hope that the blog provides solid information and leads people to interesting articles, that’s not why I do it. Rather the blog serves to meet two goals, both directly related to potential cash. First, the blog is an ongoing update of my monograph Computational Organic Chemistry and so the blog serves as both a way to make the book more valuable to its owners and as a great advertisement for the book – hopefully leading to continuing new sales (like right here!). Second, the systematic blogging builds up materials for a new edition of the book that I hope to begin serious work on in 2011. These blog posts will certainly help reduce the time I anticipate needing to invest in the revisions. I hope the next edition can be as successful as the first has been so far.

So, I’d really like to encourage more people to be creative about making chemical blogs viable. I enjoy many of my colleagues’ blogs, and I wish they would blog more often and that others would also step into the breach. I moved the blog and the book website off of the university campus not just to take advantage of the services that the web host provides (like back-up and 24/7 availability, etc.), but to allow for the possibility of making the sites more commercial – like by including fixed ads or Google ads. I haven’t done this because the blog is really self-sustaining right now, but this route might be a way for more people to think about starting their own blogs.

And I’d like to see more serious scientific blogging that acts to push the boundaries of how we can use this technology to enhance our scientific communication. Remember, we are the chemistry community and if enough of us make this technology our own, others will have to take it seriously and adopt new communication modes. Otherwise, we are stuck kowtowing to the whims and fears of publishers and scientists afraid of the new.

Following up on his previous studies of isotope effects on the ring opening of cyclopropylcarbinyl radical 1 to give 2 (see my previous post), Borden now reports on its kinetic isotope effect (KIE).¹

Using the small-curvature tunneling approximation along with structures and frequencies computed at B3LYP/6-31G(d), he finds a negligible KIE at C₁, consistent with little motion of C₁ in the transition vector. The KIE for substitution at C₄ is large (k(¹²C/¹⁴C)=5.46), also consistent with its large motion in the transition vector. What is surprising is the KIE for deuterium substitution at C₁: 0.37. This is a large inverse isotope effect!

Analysis of the vibrational frequencies that involve the C₁ hydrogens provides an explanation. In going to the TS for the ring opening, both the torsional motion about the C₁-C₂ bond (making the double bond) and the pyramidal motion increase in frequency. This leads to a higher activation barrier for H than D, and the inverse isotope effect.

References

(1) Zhang, X.; Datta, A.; Hrovat, D. A.; Borden, W. T., “Calculations Predict a Large Inverse H/D Kinetic Isotope Effect on the Rate of Tunneling in the Ring Opening of Cyclopropylcarbinyl Radical,” J. Am. Chem. Soc., 2009, 131, 16002-16003, DOI: 10.1021/ja907406q.