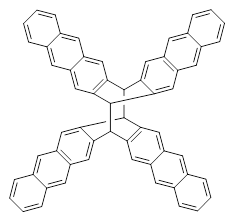
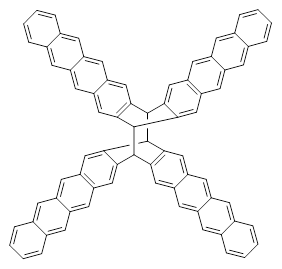
The role of dispersion in large systems is increasingly recognized as critical towards understanding molecular geometry. An interesting example is this study of acene dimers by Grimme.¹ The heptacene and nonacene dimers (1 and 2) were investigated with an eye towards the separation between the “butterfly wings” – is there a “stacked” conformation where the wings are close together, along with the “open” conformer?

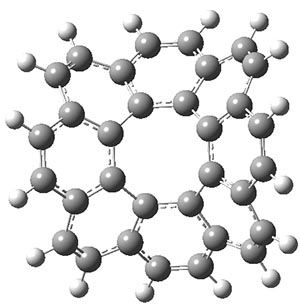
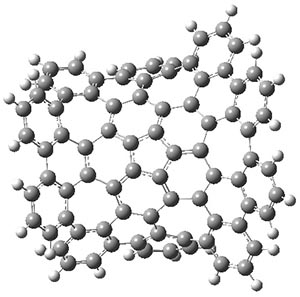
The LPNO-CEPA/CBS potential energy surface of 1 shows only a single local energy minima, corresponding to the open conformer. B3LYP-D3 and B3LYP-NL, two different variations of dealing with dispersion (see this post), do a reasonable job at mimicking the LPNO-CEPA results, while MP2 indicates the stacked conformer is lower in energy than the open conformer.

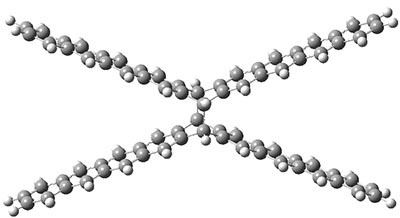
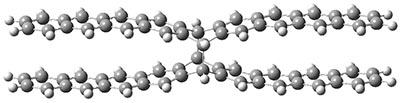
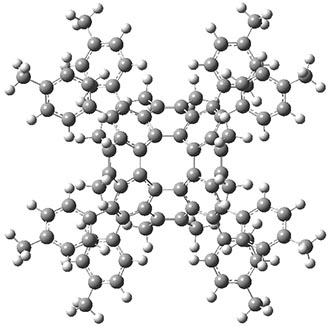
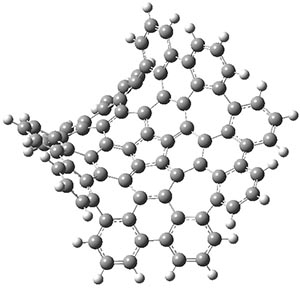
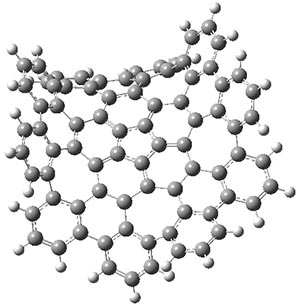
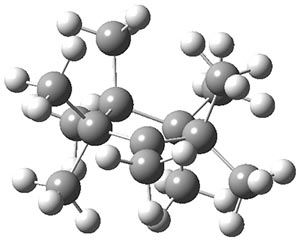
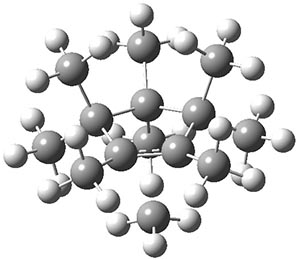
B3LYP-D3 predicts both conformers for the nonacene dimer 2, and the optimized structures are shown in Figure 2. The stacked conformer is slightly lower in energy than the open one, with a barrier of about 3.5 kcal mol^-1. However in benzene solution, the open conformer is expected to dominate due to favorable solvation with both the interior and exterior sides of the wings.

open

stacked

Figure 1. B3LYP-D3/ef2-TZVP optimized structures of the open and stacked conformations of 2.

References

(1) Ehrlich, S.; Bettinger, H. F.; Grimme, S. "Dispersion-Driven Conformational Isomerism in σ-Bonded Dimers of Larger Acenes," Angew. Chem. Int. Ed. 2013, 41, 10892–10895, DOI: 10.1002/anie.201304674.

InChIs

1: InChI=1S/C60H36/c1-2-10-34-18-42-26-50-49(25-41(42)17-33(34)9-1)57-51-27-43-19-35-11-3-4-12-36(35)20-44(43)28-52(51)58(50)60-55-31-47-23-39-15-7-5-13-37(39)21-45(47)29-53(55)59(57)54-30-46-22-38-14-6-8-16-40(38)24-48(46)32-56(54)60/h1-32,57-60H
InChIKey=OYVUURMCCBPDLI-UHFFFAOYSA-N

2: InChI=1S/C76H44/c1-2-10-42-18-50-26-58-34-66-65(33-57(58)25-49(50)17-41(42)9-1)73-67-35-59-27-51-19-43-11-3-4-12-44(43)20-52(51)28-60(59)36-68(67)74(66)76-71-39-63-31-55-23-47-15-7-5-13-45(47)21-53(55)29-61(63)37-69(71)75(73)70-38-62-30-54-22-46-14-6-8-16-48(46)24-56(54)32-64(62)40-72(70)76/h1-40,73-76H
InChIKey=FTSMWBVFVPAXOB-UHFFFAOYSA-N

The singlet and triplet carbene is the topic of Chapter 4, especially sections 1 and 2. The ground state of methylene is the triplet, with one electron in the σ-orbital and one electron in the π-orbital, with the spins aligned. The lowest singlet state places the pair of electrons in the σ-orbital, and this state is about 9 kcal mol^-1 higher in energy than the triplet. The next lowest singlet state has one electron in each of the σ- and π-orbitals, with the spins aligned. The singlet state with both electrons in the π-orbital is the highest of these four states, some 60 kcal mol^-1 above the ground state triplet.

Hoffmann and Borden now pose the question “Can the doubly occupied π carbene (¹A₁-σ⁰π²) be the ground state with appropriate substitution?” The answer they find is yes!¹

The trick is to find a combination of substituents that will raise the energy of the σ-orbital and lower the energy of the π-orbital. The latter effect can be enhanced if the π-orbital can be a part of an aromatic (6e^–) ring.

Two of the best possibilities for identifying a ground state ¹A₁-σ⁰π² carbene are 1 and 2. The CASSCF/6-31G(d) optimized geometries of these two are shown in Figure 1. In 1, the nitrogen lone pairs act to destabilize the σ-orbital, while the aldehyde group acts as a withdrawing group to stabilize the π-orbital. The result is that the ¹A₁-σ⁰π⁶ state of 1 is predicted to be about 8 kcal mol^-1 more stable than the triplet state, as per CASPT2 and CCSD(T) computations.

An ever greater effect is predicted for 2. Here the nitrogen lone pairs adjacent to the carbene act to destabilize the σ-orbital. The empty π-orbital on B lowers the energy of the carbene π-orbital by making it part of the 6-electron aromatic ring. The ¹A₁-σ⁰π⁶ state of 2 is predicted to be about 25 kcal mol^-1 more stable than its triplet state!

1

2

Figure 1. CASSCF/6-31G(d) optimized geometries of the ¹A₁-σ⁰π⁶ states of 1 and 2.

References

(1) Chen, B.; Rogachev, A. Y.; Hrovat, D. A.; Hoffmann, R.; Borden, W. T. "How to
Make the σ⁰π² Singlet the Ground State of Carbenes," J. Am. Chem. Soc. 2013, 135, 13954-13964, DOI: 10.1021/ja407116e.

InChIs

1: InChI=1S/C5H2N2O2/c8-1-4-5(2-9)7-3-6-4/h1-2H
InChIKey=QDSVROXEBBWIOO-UHFFFAOYSA-N

2: InChI=1S/C3H3BN2/c1-4-2-6-3-5-1/h1-2,4H
InChIKey=MQJXDZBYOSOLST-UHFFFAOYSA-N

What is the closest non-bonding H^…H distance within a single molecule? The world record had been 1.617 Å in a pentacyclodecane.¹ This record now appears to be broken by the preparation of the disilane 1.² The ¹H NMR and IR suggest the interior hydrogens are very close. The x-ray structure of 1 indicates a very short Si-Si distance of 4.433 Å, a distance that must accommodate two S-H bonds, typically about 1.48 Å and the H^…H non-bonded distance, which might be as short then as 1.47 Å! The crystal is unfortunately not large enough for a neutron diffraction study, which would enable precise location of the hydrogens.

1

However, computations can help here, and they suggest a H^…H separation of only 1.57 Å: this is the distance obtained with B3PW91/6-311+G(2d,p), M062x/6-311+G(2d,p) and MP2/6-31G(d). The M062x/6-311+G(2d,p) structure is shown in Figure 1.

Figure 1. The M062x/6-311+G(2d,p) optimized structure of 1.

Any ideas for a compound with an even shorter non-bonded H^…H distance?

References

(1) Ermer, O.; Mason, S. A.; Anet, F. A. L.; Miura, S. S. "Ultrashort nonbonded hydrogen^…hydrogen distance in a half-cage pentacyclododecane," J. Am. Chem. Soc. 1985, 107, 2330-2334, DOI: 10.1021/ja00294a023.

(2) Zong, J.; Mague, J. T.; Pascal, R. A. "Exceptional Steric Congestion in an in,in-Bis(hydrosilane)," J. Am. Chem. Soc. 2013, 135, 13235-13237, DOI: 10.1021/ja407398w.

InChI

1: InChI=1S/C39H32S3Si2/c1-7-19-34-28(13-1)25-40-31-16-4-10-22-37(31)44-38-23-11-5-17-32(38)41-26-29-14-2-8-20-35(29)43(34)36-21-9-3-15-30(36)27-42-33-18-6-12-24-39(33)44/h1-24,43-44H,25-27H2
InChIKey=SBEUQCUCKCNPCC-UHFFFAOYSA-N

One of the more controversial components of Bader’s Atoms-In-Molecules (AIM) theory is the contention that there is a one-to-one correspondence between the existence of a bond critical point and the existence of a chemical bond. I discuss this matter in my book and also in these posts (1 and 2). Lane and co-workers now examine this relationship with regard to hydrogen bonds.¹

They examine the topological structure of the electron density of the series 1,2-ethanediol 1, 1,3-propanediol 2, and 1,3-butanediol 3. They find a bond critical point (bcp) between the hydrogen of one hydroxyl group and the oxygen of the second hydroxyl group for the two large compounds 2 and 3. This forms a ring, and a ring critical point is located as well. However, for 1 they find no bond critical point associated with what might be the intramolecular hydrogen bond in 1. For all three diols, the OH stretching frequencies are diminished relative to monoalcohols. So geometrically and spectroscopically there appears to be a hydrogen bond, but rigorous application of Bader’s notion of bonding says that there is no “bond” in 1.

Lane and coworkers go on to show that the electron density in the three diols is really topologically identical, just differing in a matter of degree. They conclude that the existence of a bond critical point should not be the sole arbiter of bonding, but one of the criteria that can be utilized to assess bonding.

While I am not at all in conflict with this conclusion, the paper contains some issues that need be addressed. First off, “bonding” is not a concept of either-or, rather there is a continuum of bonding. Hydrogen bonding should not at all be confused with covalent or ionic bonding – it is dramatically weaker and so one might consider whether the bcp criteria is applicable at all. The authors really fall into this trap stating “… the absence of a BCP should not necessarily be considered evidence as to the absence of a chemical bond (emphasis mine).” Do we want to consider a hydrogen bond as a chemical bond?

I think the key element overlooked in this study is the strength of the “hydrogen bond”. While not determined in the study, undoubtedly the hydrogen bond strength increases in the order 1 < 2 < 3. What is really to be gained by arguing there is or is not a “hydrogen bond” in all or some of these three molecules? The ring-like conformation is the lowest energy conformation for all three. This is driven by some electrostatic attraction between the OH dipole of one hydroxyl group for the dipole of the second hydroxyl group. When do we want to call this attraction a hydrogen bond? What do we gain by not doing so for all three? If we understand that there is an energy continuum of hydrogen bonding, from weak to weaker, doesn’t that provide enough of a model to interpret and predict chemical structure and behavior?

References

(1) Lane, J. R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B. J.; Kjaergaard, H. G. J. Chem. Theor. Comput. 2013, 9, 3263-3266, DOI: DOI: 10.1021/ct400420r.

InChIs

1: InChI=1S/C2H6O2/c3-1-2-4/h3-4H,1-2H2
InChIKey=>LYCAIKOWRPUZTN-UHFFFAOYSA-N

2: InChI=1S/C3H8O2/c4-2-1-3-5/h4-5H,1-3H2
InChIKey=YPFDHNVEDLHUCE-UHFFFAOYSA-N

3: InChI=1S/C4H10O2/c5-3-1-2-4-6/h5-6H,1-4H2
InChIKey=WERYXYBDKMZEQL-UHFFFAOYSA-N

A long sought-after data point critical to the non-classical cation story has finally been obtained. The elusive x-ray crystal structure of a norbornyl cation was finally solved.¹ The [C₇H₁₁]⁺[Al₂Br₇]^– salt was crystallized in CH₂Br₂ at low temperature (40 K). This low temperature was needed to prohibit rotation of the norbornyl cation within the crystal (the cation is near spherical and so subject to relatively easy rotation within the crystal matrix) and hydride scrambling among the three carbons (C₁, C₂, and C₆) involved in the non-classical cation structure.

The authors report a number of different structures, all very similar, depending on slight differences in the crystals used. However, the important features are consistent with all of the structures. The cation is definitely of the non-classical type (see Figure 1) with the basal C₁-C₂ bond length of 1.39 Å similar that in benzene and long non-classical C₁-C₆ and C₂-C₆ distances of 1.80 Å. These distances match very well with the MP2(FC)/def2-QZVPP optimized distances of 1.393 and 1.825 Å, respectively.

Figure 1. X-ray structure of norbornyl cation.

References

(1) Scholz, F.; Himmel, D.; Heinemann, F. W.; Schleyer, P. v. R.; Meyer, K.; Krossing, I. "Crystal Structure Determination of the Nonclassical 2-Norbornyl Cation," Science 2013, 341, 62-64, DOI: 10.1126/science.1238849.

Circulenes are molecules where a central ring is composed of fused benzenoids. Corranulene can also be named [5]circulene and coronene is [6]circulene. In a previous post I discussed the topology of the circulenes. This earlier work suggested that [8]annulene 1 would have a saddle-shape. This hypothesis has now been confirmed with the synthesis of the substituted [8]circulene 2 by Wu and co-workers.¹

The x-ray structure does show a saddle geometry for 2. The central 8-member ring is tub-shaped, even more puckered that cyclooctatetraene (COT) itself, though the bonds in 2 are nearly of equal length. The bond lengths involving the central carbon atoms appear consistent with an [8]radialene-type structure.

The ωB97X-D/6-31G** optimized geometries of the parent compound 1 and the synthesized compound 2 are shown in Figure 1. These computed structures are very similar to each other, along with being very similar to the x-ray structure of 2.

1

2

Figure 1. ωB97X-D/6-31G** optimized geometries of 1 and 2.
(Don’t forget that you can click on these structures – and any other structure on my blog – to interactively manipulate and visualize them, something worth doing here!)

The computed NICS(0) (at HF/6-31+G* – I would really rather have seen these computed with some density functional, preferably at ωB97X-D/6-31G**) values for the six-member rings of both 1 and 2 are negative, ranging from -8.9 ppm to -4.0 ppm, indicating aromatic character. The NICS(0) value at the center of the 8-member ring is +9.8 ppm in 1 and +12.2 ppm in 2. The authors argue that this value cannot discriminate the 8-member ring from that in COT (NICS(0) = 1.98 ppm, the expected value for a non-aromatic ring) and [8]radialene (NICS(0) = -1.2 ppm, also an expected value for a non-aromatic ring). However, they are silent on whether this might actually imply some antiaromatic character to the 8-member ring, which would be consistent with the equivalent bond lengths around the ring.

The authors note that there should be a second isomer of 2 resulting from a flip of the tub. Variable temperature NMR does not show any change in the spectrum, though with a different substituted [8]circulene they do see some coalescence, suggesting a large flipping barrier of at least 20 kcal mol^-1. A computational search for this flipping/inversion might be interesting as the transition state is likely to not be planar.

References

(1) Feng, C.-N.; Kuo, M.-Y.; Wu, Y.-T. "Synthesis, Structural Analysis, and Properties of [8]Circulenes," Angew. Chem. Int. Ed. 2013, 52, 7791-7794, DOI: 10.1002/anie.201303875.

InChIs

1: InChI=1S/C32H16/c1-2-18-5-6-20-9-11-22-13-15-24-16-14-23-12-10-21-8-7-19-4-3-17(1)25-26(18)28(20)30(22)32(24)31(23)29(21)27(19)25/h1-16H
InChIKey=BASWMOIVIHXTRC-UHFFFAOYSA-N

2: InChI=1S/C96H80/c1-49-17-33-65(34-18-49)81-73-57(9)58(10)75-83(67-37-21-51(3)22-38-67)85(69-41-25-53(5)26-42-69)77-61(13)62(14)79-87(71-45-29-55(7)30-46-71)88(72-47-31-56(8)32-48-72)80-64(16)63(15)78-86(70-43-27-54(6)28-44-70)84(68-39-23-52(4)24-40-68)76-60(12)59(11)74(82(81)66-35-19-50(2)20-36-66)90-89(73)91(75)93(77)95(79)96(80)94(78)92(76)90/h17-48H,1-16H3
InChIKey=DEKWLSGHBADDAQ-UHFFFAOYSA-N

Scott and Itami report on a graphene fragment that is highly warped.¹ They have prepared 1 by three separate procedures, one of which starts with corranulene and in two steps makes the product!

The five 7-member rings warp the structure so that it is non-planar. In fact the molecule has negative curvature, reminiscent of a riding saddle. They report the x-ray structure, outside of the fullerenes, the largest hydrocarbon reported by x-ray crystallography. Because of its non-planar geometry, 1 does not pack well and so it is soluble in a variety of solvents.

The authors have obtained the structure of 1 at B3LYP/6-31G(d), shown in Figure 1. The central corranulene component is a shallow bowl, much less shallow than in corranulene itself. This suggests that the compound might flip with a relatively low barrier. The computed barrier is only 1.7 kcal mol^-1. Due to the negative curvatures associated with the seven-member rings, 1 is chiral and the ring flipping process leaves the chirality unchanged. A second transition was located that leads to racemization through a transition state of C_s symmetry. The barrier for this racemization is computed to be 18.9 kcal mol^-1. Variable temperature ¹H NMR analysis does show that at room temperature 1 (substituted with one t-butyl ring on each of the ten exterior phenyl rings) undergoes rapid motion that equilibrates all of the protons. However, at lower temperature the signals for ring protons do separate. This leads to the barrier or the racemization process of 13.6 kcal mol^-1. The ring flip is not frozen out at the temperatures explored.

1

1-TSflip

1-TSrac

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and the transition states for flipping and racemization. (Remember that all structures in my blog are active – click on them to run Jmol and manipulate the 3-D structure.)

Compound 1 is an example of a very interesting negative curvature hydrocarbon, especially unusual for what might be considered an aromatic compound.

References

(1) Kawasumi, K.; Zhang, Q.; Segawa, Y.; Scott, L. T.; Itami, K. "A grossly warped nanographene and the consequences of multiple odd-membered-ring defects," Nat Chem 2013, advance online publication, DOI: 10.1038/nchem.1704.

InChIs

1: InChI=1S/C80H30/c1-11-31-32-12-2-23-43-44-24-5-15-35-36-16-6-27-47-48-28-9-19-39-40-20-10-30-50-49-29-8-18-38-37-17-7-26-46-45-25-4-14-34-33-13-3-22-42-41(21-1)51(31)61-62(52(32)43)72-65(55(35)44)66(56(36)47)74-69(59(39)48)70(60(40)50)75-68(58(38)49)67(57(37)46)73-64(54(34)45)63(53(33)42)71(61)76-77(72)79(74)80(75)78(73)76/h1-30H
InChIKey=KMAOOAQTQHCOHV-UHFFFAOYSA-N

The nine methyl groups of nonamethylcyclopentyl cation 1 all interconvert with a barrier of 7 kcal mol^-1. However, at low temperature only partial scrambling occurs: there are two sets of methyl groups, one containing five groups and the other containing four methyl groups. The barrier for this scrambling is only 2.5 kcal mol^-1. While this behavior was found more than 20 years ago, Tantillo and Schleyer¹ only now have offered a complete explanation.

1

The ground state structure of 1 is shown in Figure 1 and has C₁ symmetry. The two pseudo-axial methyl groups adjacent to the cationic center show evidence of hyperconjugation: long C-C bonds and Me-C-C⁺ angles of 100°.

The transition state TS1¸also in Figure 1, is of C_s symmetry. This transition state leads to interchange of the pseudo-axial methyls, and interchange of the pseudo-equatorial methyls, but no exchange between the members of these two groups. The M06-2x/6-31+G(d,p) and mPW1PW91/6-31+G(d,p) estimate of this barrier is 1.5 and 2.5 kcal mol^-1, respectively. This agrees well with the experiment.

1
TS1	TS2

Figure 1. B3LYP/6-3+G(d,p) optimized geometries.

A second transition state TS2 was found and it corresponds with a twisting motion that interconverts an axial methyl with an equatorial methyl. This TS has C_s symmetry (shown in Figure 1) and the eclipsing interaction give rise to a larger barrier: 7.3 (M06-2x/6-31+G(d,p)) and 6.7 kcal mol^-1 (mPW1PW91/6-31+G(d,p)). So twisting through TS2 and scrambling through TS1 allows for complete exchange of all 9 methyl groups.

An interesting point also made by these authors is that these three structures represent the continuum of cationic structure: a classical (localized) cation in TS2, a bridged structure in TS1 and hyperconjugated cation in 1.

References

(1) Tantillo, D. J.; Schleyer, P. v. R. “Nonamethylcyclopentyl Cation Rearrangement Mysteries Solved,” Org. Lett. 2013, 15, 1725-1727, DOI: 10.1021/ol4005189.

InChIs

1: InChI=1S/C14H27/c1-10-11(2,3)13(6,7)14(8,9)12(10,4)5/h1-9H3/q+1
InChIKey=WUGVCUSQGLXERW-UHFFFAOYSA-N

One of the most widely recognized principles within organic chemistry is Hückel’s rule: an aromatic compound possesses 4n+2 π-electrons while an antiaromatic compound possesses 4n π-electrons. Much less well known is Baird’s rule:¹ the first excited triplet state will be aromatic if it has 4n π-electrons and antiaromatic if it has 4n+2 π-electrons.²

Schleyer used a number of standard methods for assessing aromatic character of a series of excited state triplets, including NICS values and geometric parameters.³ However, Schleyer has long been a proponent of an energetic assessment of aromaticity and it is only now in this recent paper⁴ that he and co-workers examine the stabilization energy of excited triplet states. The isomerization
stabilization energy (ISE)⁵ compares an aromatic (or antiaromatic) compound against a non-aromatic reference, one that typically is made by appending an exo-methylene group to the ring. So, to assess the ISE of the T₁ state of benzene, Reaction 1 is used. (Note that the inherent assumption here is that the stabilization energy of benzene is essentially identical to that of toluene.) At B3LYP/6-311++G(d,p) the energy of Reaction 1 is +13.5 kcal mol^-1. This reaction should be corrected for non-conservation of s-cis and s-trans conformers by adding on the energy of Reaction 2, which is +3.4 kcal mol^-1. So, the ISE of triplet benzene is +16.9 kcal mol^-1, indicating that it is antiaromatic. In contrast, the ISE for triplet cyclooctatetraene is -15.6 kcal mol^-1, and when corrected its ISE value is -24.7 kcal mol^-1, indicating aromatic character. These are completely consistent with Baird’s rule. Schleyer also presents an excellent correlation between the computed ISE values for the triplet state of 9 monocyclic polyenes and their NICS(1)_zz values.

I want to thank Henrik Ottosson for bringing this paper to my attention and for his excellent seminar on the subject of Baird’s rule on his recent visit to Trinity University.

References

(1) Baird, N. C. "Quantum organic photochemistry. II. Resonance and aromaticity in
the lowest 3ππ* state of cyclic hydrocarbons," J. Am. Chem. Soc. 1972, 94, 4941-4948, DOI: 10.1021/ja00769a025.

(2) Ottosson, H. "Organic photochemistry: Exciting excited-state aromaticity," Nat Chem 2012, 4, 969-971, DOI: 10.1038/nchem.1518.

(3) Gogonea, V.; Schleyer, P. v. R.; Schreiner, P. R. "Consequences of Triplet Aromaticity in 4nπ-Electron Annulenes: Calculation of Magnetic Shieldings for Open-Shell Species," Angew. Chem. Int. Ed. 1998, 37, 1945-1948, DOI: 10.1002/(SICI)1521-3773(19980803)37:13/14<1945::AID-ANIE1945>3.0.CO;2-E.

(4) Zhu, J.; An, K.; Schleyer, P. v. R. "Evaluation of Triplet Aromaticity by the
Isomerization Stabilization Energy," Org. Lett. 2013, 15, 2442-2445, DOI: 10.1021/ol400908z.

(5) Schleyer, P. v. R.; Puhlhofer, F. "Recommendations for the Evaluation of Aromatic Stabilization Energies," Org. Lett. 2002, 4, 2873-2876, DOI: 10.1021/ol0261332.

Jacobsen reports on another application of thiourea-based organocatalysts, this time for the
catalysis of hydroamination.¹ To support the synthetic effort, he examined the uncatalyzed intramolecular hydroamination that takes 1, through TS1 into product 2. The geometry of TS1 optimized at B3LYP/6-31+G(d,p) is shown in Figure 1. The computed barrier for this reaction is 22.2 kcal mol^-1. Using a model thiourea as the catalyst (MeHN)₂C=S, 3), Jacobsen locates a
catalyzed transition state TS2 shown in Figure 1. The activation barrier for this catalyzed reaction is 19.1 kcal mol^-1, suggesting that a thiourea can afford a real catalytic effect.

TS1

TS2

Figure 1. B3LYP/6-31+G(d,p) optimized geometries of TS1 and TS2(the catalyzed transition state).

Jacobsen then goes on to show that 4 can act as both an excellent catalyst for the hydroamination reaction along with inducing significant enantioselectivity. An example is Reaction 1, where 10 mol% of catalyst 3 gives an overall yield of 83% and an ee of 91%, while in the absence of catalyst the yield is only 8%.

References

(1) Brown, A. R.; Uyeda, C.; Brotherton, C. A.; Jacobsen, E. N. "Enantioselective Thiourea-Catalyzed Intramolecular Cope-Type Hydroamination," J. Am. Chem. Soc. 2013, 135, 6747-6749, DOI: 10.1021/ja402893z.

InChIs

1: InChI=1S/C5H11NO/c1-2-3-4-5-6-7/h2,6-7H,1,3-5H2
InChIKey=JUMXQRNWLGIKEI-UHFFFAOYSA-N

2: InChI=1S/C5H11NO/c1-5-3-2-4-6(5)7/h5,7H,2-4H2,1H3
InChIKey=YVBPNYXAQNAMLH-UHFFFAOYSA-N

3: InChI=1S/C3H8N2S/c1-4-3(6)5-2/h1-2H3,(H2,4,5,6)
InChIKey=VLCDUOXHFNUCKK-UHFFFAOYSA-N

4: InChI=1S/C44H49N3OS/c1-44(2,3)42(41(48)36-25-15-24-35(36)34-23-14-21-30-16-10-11-22-33(30)34)46-43(49)45-37-26-12-13-27-40(37)47-38(31-17-6-4-7-18-31)28-29-39(47)32-19-8-5-9-20-32/h4-11,14,16-23,28-29,35-37,40,42H,12-13,15,24-27H2,1-3H3,(H2,45,46,49)/t35-,36?,37-,40-,42-/m1/s1
InChIKey=OJMZMPGOFWBKAF-FDGFXIECSA-N