One of the more controversial components of Bader’s Atoms-In-Molecules (AIM) theory is the contention that there is a one-to-one correspondence between the existence of a bond critical point and the existence of a chemical bond. I discuss this matter in my book and also in these posts (1 and 2). Lane and co-workers now examine this relationship with regard to hydrogen bonds.1
They examine the topological structure of the electron density of the series 1,2-ethanediol 1, 1,3-propanediol 2, and 1,3-butanediol 3. They find a bond critical point (bcp) between the hydrogen of one hydroxyl group and the oxygen of the second hydroxyl group for the two large compounds 2 and 3. This forms a ring, and a ring critical point is located as well. However, for 1 they find no bond critical point associated with what might be the intramolecular hydrogen bond in 1. For all three diols, the OH stretching frequencies are diminished relative to monoalcohols. So geometrically and spectroscopically there appears to be a hydrogen bond, but rigorous application of Bader’s notion of bonding says that there is no “bond” in 1.
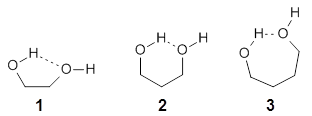
Lane and coworkers go on to show that the electron density in the three diols is really topologically identical, just differing in a matter of degree. They conclude that the existence of a bond critical point should not be the sole arbiter of bonding, but one of the criteria that can be utilized to assess bonding.
While I am not at all in conflict with this conclusion, the paper contains some issues that need be addressed. First off, “bonding” is not a concept of either-or, rather there is a continuum of bonding. Hydrogen bonding should not at all be confused with covalent or ionic bonding – it is dramatically weaker and so one might consider whether the bcp criteria is applicable at all. The authors really fall into this trap stating “… the absence of a BCP should not necessarily be considered evidence as to the absence of a chemical bond (emphasis mine).” Do we want to consider a hydrogen bond as a chemical bond?
I think the key element overlooked in this study is the strength of the “hydrogen bond”. While not determined in the study, undoubtedly the hydrogen bond strength increases in the order 1 < 2 < 3. What is really to be gained by arguing there is or is not a “hydrogen bond” in all or some of these three molecules? The ring-like conformation is the lowest energy conformation for all three. This is driven by some electrostatic attraction between the OH dipole of one hydroxyl group for the dipole of the second hydroxyl group. When do we want to call this attraction a hydrogen bond? What do we gain by not doing so for all three? If we understand that there is an energy continuum of hydrogen bonding, from weak to weaker, doesn’t that provide enough of a model to interpret and predict chemical structure and behavior?
References
(1) Lane, J. R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B. J.; Kjaergaard, H. G. J. Chem. Theor. Comput. 2013, 9, 3263-3266, DOI: DOI: 10.1021/ct400420r.
InChIs
1: InChI=1S/C2H6O2/c3-1-2-4/h3-4H,1-2H2
InChIKey=>LYCAIKOWRPUZTN-UHFFFAOYSA-N
2: InChI=1S/C3H8O2/c4-2-1-3-5/h4-5H,1-3H2
InChIKey=YPFDHNVEDLHUCE-UHFFFAOYSA-N
3: InChI=1S/C4H10O2/c5-3-1-2-4-6/h5-6H,1-4H2
InChIKey=WERYXYBDKMZEQL-UHFFFAOYSA-N

Henry Rzepa responded on 25 Sep 2013 at 4:38 am #
Steve is correct; interpreting the existence or non-existence of a “bond” by whether there is a bond critical point (bcp) is not sound. As I have often pointed out, according to the Poincare-Hopf theorem, a bcp can be annihilated by an adjacent rcp. So in a small ring, such annihilation can occur much more easily than in a large ring. This does not mean the small ring H-bond is in any way “different”. The best example of this is the bcp in cis-butene, where a H…H interaction is so characterised (but it is on the verge of annihilation with a nearby rcp). I think it is now accepted that this H…H interaction is not actually attractive in any manner, but in fact repulsive!
What one may be able to do is to look at WHERE along a bond the bcp coordinates are. This might then tell how how acidic the H is, and possibly other interesting information about the hydrogen bond.
But there are many ways of characterising such weak interactions. For example, I explored the NBO approach on my blog and one can also use the density gradient in the so-called NCI (non-covalent interactions) approach (doi: 10.1021/ja100936w).
In the “weak” region of electron density, where many interactions exist (hydrogen bond, dispersion, electrostatic, etc) it is indeed difficult to define the boundaries between what a bond, an attractive interaction and a repulsive interaction are.
Ilmu Kimia responded on 26 Sep 2013 at 5:43 pm #
So I never know that hydrogen bond has critical points.
Thank you for the lessons.
Theodore S. Dibble responded on 26 Sep 2013 at 7:15 pm #
This issue has relevance to atmospheric and combustion chemistry of alkoxy and peroxy radical analogs of 1–3. Activation barriers and densities of states depend on the presence and strength of the hydrogen bonds (or attractive interactions).
Tiago Galvão responded on 11 Dec 2013 at 5:31 pm #
From the conclusions obtained in the paper bellow, it is possible to extrapolate that a BCP doesn´t form in 1, due to the fact that the interation of the two oxygen electron density prevails. In our study, we verified the Baker and Hubbard geometric rule for hydrogen bonds with QTAIM.
http://pubs.acs.org/doi/abs/10.1021/jp410004x
From 2-Hydroxypyridine to 4(3H)-Pyrimidinone: Computational Study on the Control of the Tautomeric Equilibrium