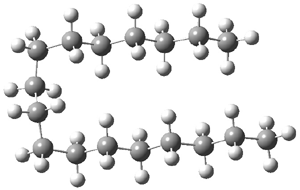
I have written a number of posts discussing long C-C bonds (here and here). What about very long bonds between carbon and a heteroatom? Well, Mascal and co-workers¹ have computed the structures of some oxonium cations that express some very long C-O bonds. The champion, computed at MP2/6-31+G**, is the oxatriquinane 1, whose C-O bond is predicted to be 1.602 Å! (It is rather disappointing that the optimized structures are not included in the supporting materials!) The long bond is attributed not to dispersion forces, as in the very long C-C bonds (see the other posts), but rather to σ(C-H) or σ(C-C) donation into the σ*(C-O) orbital.

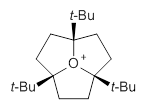
1

Inspired by these computations, they went ahead and synthesized 1 and some related species. They were able to get crystals of 1 as a (CHB₁₁Cl₁₁)^– salt. The experimental C-O bond lengths for the x-ray crystal study are 1.591, 1.593, and 1.622 Å, confirming the computational prediction of long C-O bonds.

As an aside, they also noted many examples of very long C-O distances within the Cambridge
Structural database that are erroneous – a cautionary note to anyone making use of this database to identify unusual structures.

References

(1) Gunbas, G.; Hafezi, N.; Sheppard, W. L.; Olmstead, M. M.; Stoyanova, I. V.; Tham, F. S.; Meyer, M. P.; Mascal, M. "Extreme oxatriquinanes and a record C–O bond length," Nat. Chem. 2012, 4, 1018-1023, DOI: 10.1038/nchem.1502

InChIs

1: InChI=1S/C21H39O/c1-16(2,3)19-10-12-20(17(4,5)6)14-15-21(13-11-19,22(19)20)18(7,8)9/h10-15H2,1-9H3/q+1/t19-,20+,21-
InChIKey=VTBHIDVLNISMTR-WKCHPHFGSA-N

The role of dispersion in understanding organic chemistry, both structure and reactivity, is truly coming into prominence (see for example this blog post for a compound whose stability is the result of dispersion). This has been driven in part by new computational techniques to properly account for dispersion. An interesting recent example is the structure of long chain alkanes, with a question posed and answered by Mata and Suhm:¹ What is the largest alkane whose most stable conformation is the extended chain?

The question is attacked by computation and experiment. The computational methodology involves corrections to the local MP2-F12 energy involving the separation of orbital pairs that are treated with a coupled clusters method. The straight chain (having only anti arrangements about the C-C bonds) and the hairpin conformer (having three gauche arrangements) were completely optimized. The C₁₇H₃₆ hairpin isomer is shown in Figure 1. For chains with 16 or fewer carbons, the all-anti straight chain is lower in energy, but for chains with 17 or more carbon atoms, the hairpin is lower in energy. Gas-phase low temperature IR and Raman spectra suggest that dominance of the hairpin occurs when the chain has 18 carbons, though careful analysis suggests that this is likely an upper bound. At least tentatively the answer to the question is that heptadecane is likely the longest alkane with a straight chain, but further lower temperature experiments are needed to see if the C16 chain might fold as well.

Figure 1. Optimized geometry of the hairpin conformation of heptadecane.

(I thank Dr. Peter Schreiner for bringing this paper to my attention.)

References

(1) Lüttschwager, N. O. B.; Wassermann, T. N.; Mata, R. A.; Suhm, M. A. "The Last Globally Stable Extended Alkane," Angew. Chem. Int. Ed. 2012, ASAP, DOI: 10.1002/anie.201202894.

InChIs

Heptadecane: InChI=1S/C17H36/c1-3-5-7-9-11-13-15-17-16-14-12-10-8-6-4-2/h3-17H2,1-2H3
InChIKey=NDJKXXJCMXVBJW-UHFFFAOYSA-N

The combined supersonic jet expansion and Fourier transform microwave spectroscopy provides an excellent opportunity for the synergistic workings of experiments and computations. This is nicely demonstrated in the study of 1-methyl-4-piperidone.¹

The careful microwave study allows for the full structural characterization of the equatorial form 1e along with obtaining a good deal of information concerning the axial form 1a. To help evaluate the experimental data, the authors have optimized the structure of the two isomers at MP2, B3LYP and M06-2x using the 6-311++G(d,p) basis set.

The rotational parameters computed with the three methods are in very fine agreement with the experimental values. Of particular note is that the three computations predict a different sign for the nuclear quadrupole coupling tensor elements χ_aa and χ_bb, and this is observed in the experiment as well. It is perhaps the critical identifier of the axial isomer. The computed and experimental geometries of 1e are in fine agreement, with the largest deviation of a few degrees in the dihedral angle of the carbonyl to the ring. The experiment suggests an energy difference of 11.9 kJ mol^-1, which is corroborated by MP2, B3LYP and M06-2x computations. In fact, these first two methods predict an enthalpy difference within a kJ of the experimental value.

References

(1) Evangelisti, L.; Lesarri, A.; Jahn, M. K.; Cocinero, E. J.; Caminati, W.; Grabow, J.-U., "N-Methyl Inversion and Structure of Six-Membered Heterocyclic Rings: Rotational Spectrum of 1-Methyl-4-piperidone," J. Phys. Chem. A, 2011,
115, 9545–9551, DOI: 10.1021/jp112425w

InChIs

1: InChI=1/C6H11NO/c1-7-4-2-6(8)3-5-7/h2-5H2,1H3
InChIKey=HUUPVABNAQUEJW-UHFFFAOYAT

I am very much contemplating a second edition of my book Computational Organic Chemistry, which is the basis of this blog. I have been in touch with Wiley and they are enthusiastic about a second edition.

Here is a list of some of the things I am contemplating as new topics for the second edition

1. Discussion of the failures of many of the standard functionals (like B3LYP) to treat simple organics
2. Predicting NMR, IR and ORD spectra
3. Möbius compounds, especially aromatics
4. π-π-stacking
5. tunneling in carbenes (Schreiner and Allen’s great work)
6. acidity of amino acids and remote protons
7. bifurcating potential energy surfaces and the resultant need for dynamic considerations
8. even more examples of dynamics – especially the roundabout S_N2

So, I would like to ask my readers for suggestions of other ideas for new topics to add to the book. These can be extensions of the topics already covered, or brand new areas!

Additionally, I am planning on interviewing a few more people for the book, similar in spirit to the 6 interviews in the first addition. Again, I welcome any suggestions for computational chemists to interview!

Laane has utilized high level computations to examine the high resolution IR and raman spectra of cyclopentane and some deuterated isomers.¹ What is particularly of interest here is the excellent agreement between the experiment and computations. The barrier for planarity is estimated from experiment to be 1808 cm^-1 and CCSD/cc-pVTZ predicts a value of 1887 cm^-1 – excellent agreement. The B3LYP/cc-pVTZ computed frequencies for the C₂ and C_i conformations were scaled by 0.985 for frequencies less than 1450 cm^-1, 0.975 for frequencies between 1450 and 200 cm^-1 and by 0.961 for frequencies above 2000 cm^-1. These frequencies are very similar to one another. In comparison of these averaged frequencies with the experimental frequencies the root mean squared error is only 8.8 cm^-1! As stressed by these authors, computational is important partner with experiment in characterizing spectra.

References

(1) Ocola, E. J.; Bauman, L. E.; Laane, J., "Vibrational Spectra and Structure of Cyclopentane and its Isotopomers," J. Phys. Chem. A, 2011, 115, 6531–6542, DOI: 10.1021/jp2032934.

InChIs

Cyclopentane: InChI=1/C5H10/c1-2-4-5-3-1/h1-5H2 InChIKey=RGSFGYAAUTVSQA-UHFFFAOYAL

Compounds like antipyrine 1 might be expected to have two pyramidal nitrogens with their substituents on opposite sides of the ring. Interestingly, a new polymorph of propyphenazone 2 has both N-methyl and N-phenyl groups on the same side of the ring. Just how unusual is this?

Roumanos and Kertesz¹ have sampled the crystallographic database and found 334 structures with the antipyrine backbone. The vast majority of them have the nitrogen substituents on opposite sides, and a few structures have these groups essential co-planar with the ring. The new propyphenazone structure does seem to be unusual. However, they also performed a BLYP/DNP scan of the potential energy surface of 2. When this surface is overlayed on the distribution of the x-ray structures, one sees that most structures are within 3 kcal mol^-1 of the energy minimum (with the nitrogen groups on opposite sides). However, the structure with both groups on the same side is about 4 kcal mol^-1 higher in energy than the minimum energy structure, and the nearly planar structures are higher in energy still. Thus, the authors conclude that while this new structure is unusual, it is not an outlier.

References

(1) Roumanos, M.; Kertesz, M., "Conformations of Antipyrines," J. Phys. Chem.A, 2011, ASAP, DOI: 10.1021/jp201510w

InChIs

1: InChI=1/C11H12N2O/c1-9-8-11(14)13(12(9)2)10-6-4-3-5-7-10/h3-8H,1-2H3
InChIKey=VEQOALNAAJBPNY-UHFFFAOYAS

2: InChI=1/C14H18N2O/c1-10(2)13-11(3)15(4)16(14(13)17)12-8-6-5-7-9-12/h5-10H,1-4H3
InChIKey=PXWLVJLKJGVOKE-UHFFFAOYAH

Proper handling of hydrogen bonding using DFT remains a concern. Sherrill has reported a careful benchmark study using the potential energy curves for the six dimer combinations involving formic acid, formamide, and formamidine.¹ Comparisons are made to the the CBS extrapolated limit CCSD(T) curve.

As anticipated, B3LYP and related functionals do a poor job. Interestingly, PBE and PBE0 provide very nice curves. The meta-GGA functionals like M05-2x and M06-2x and functionals with dispersion corrections (like ωB97X-D) provide very good potential energy curves. It is clear that intermediate and long-range correlation and dispersion must be accounted for when handling hydrogen bonded systems. Proper selection of the functional is critical.

References

(1) Thanthiriwatte, K. S.; Hohenstein, E. G.; Burns, L. A.; Sherrill, C. D., “Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions,” J. Chem. Theory Comput., 2011, 7, 88-96, DOI: 10.1021/ct100469b.

The structure of organic molecules of biochemical significance remains an important pursuit, one that I have discussed in a number of blog posts. Highlighted particularly in this blog (and in my book) has been the interplay of experiment and computation in structure determination. Dopfer and co-workers combine IR multiple photon dissociation (IRMPD) with DFT and MP2 computations to determine the structure of protonated serotonin 1H+.¹

B3LYP/cc-pVDZ and MP2/cc-pVDZ computations of the conformations of 1H+ give nearly identical results. The lowest energy conformer (see Figure 1) has the ethylamine group in a gauche arrangement so that the protonated amine can interact with the π-system of the ring. The hydroxyl group is orientated trans relative to the ethylamine group. Conformer generated by rotation about the C-O bond or the C-C and C-N bond of the ethylamine group are higher in energy, anywhere from 0.5 to about 5 kcal mol^-1 above the lowest conformer. Protonation at the ring nitrogen or the oxygen are more than 20 kcal mol^-1 higher in energy than the lowest conformer.

1H+

Figure 1. B3LYP/6-31G(d) optimized geometry of 1H+. Note that the authors did not supply sufficient information in their supporting materials to generate the full 3-D coordinates of the molecule, and I did not want to reoptimize at cc-pVDZ. Referees – please insist on complete supporting information!

Comparison of the experimental IR spectrum of 1H+ with the computed IR frequencies (either B3LYP or MP2 – they are very similar) reveals a remarkable agreement with the computed spectra of just the lowest energy conformer. While the lowest energy conformer is predicted to be nearly 70% of the population, there is little spectroscopic evidence of the participation of any other conformer. In fact, the next three lowest energy conformers have a distinctive peak (in their computed IR spectrum) at about 1400 cm^-1, a region that has virtually no absorption in the experimental IR.

References

(1) Lagutschenkov, A.; Langer, J.; Berden, G.; Oomens, J.; Dopfer, O., "Infrared Spectra of Protonated Neurotransmitters: Serotonin," J. Phys. Chem. A, 2010, 114, 13268-13276, DOI: 10.1021/jp109337a

InChIs

serotonin: InChI=1/C10H12N2O/c11-4-3-7-6-12-10-2-1-8(13)5-9(7)10/h1-2,5-6,12-13H,3-4,11H2
InChIKey=QZAYGJVTTNCVMB-UHFFFAOYAX

1H+: InChI=1/C10H12N2O/c11-4-3-7-6-12-10-2-1-8(13)5-9(7)10/h1-2,5-6,12-13H,3-4,11H2/p+1/fC10H13N2O/h11H/q+1
InChIKey=QZAYGJVTTNCVMB-HISXSYJOCA

This one is a bit afield from organic chemistry, but the result is important for computational chemists who are interested in electron density analysis.

The topological electron density analysis of Bader (also called Atoms-In-Molecules – AIM) carves up a molecular electron density into regions associated with an attractor. The attractor is a critical point in the electron density that is a maximum in all directions. Gradient paths, paths that trace increasing electron density, terminate at such an attractor. The union of all such paths defines a basin. Bader found that for typical molecules, the attractor is coincident with the position of the atomic nucleus. He has then assumed a 1:1 correspondence between these two – all nuclei are attractors and all attractors correspond with nuclei.

This correspondence has been questioned in computations on some metals. For example, Li_n and Na_n (n=2,4,6) have a non-nuclear attractor. However, no clear-cut unambiguous experimental observation of non-nuclear attractors has been made, until now. Platts and Stasch¹ have obtained the x-ray diffraction electron density of 1 and they find a non-nuclear attractor near the midpoint of the Mg-Mg bond. This is corroborated by DFT computations of 1 and some related systems. It should be said that the electron density along the Mg-Mg path is quite flat in the middle, but the attractor is present, and the integrated number of electrons within the basin associated with this non-nuclear attractor is a non-trivial 0.81 e (experiment) or 0.79 e (DFT).

It now appears incontrovertible that non-nuclear attractors of the molecular electron density can exist. It would be especially interesting if these types of points could be located in organic species.

References

(1) Platts, J. A.; Overgaard, J.; Jones, C.; Iversen, B. B.; Stasch, A., "First Experimental Characterization of a Non-nuclear Attractor in a Dimeric Magnesium(I) Compound," J. Phys. Chem. A, 2011, 115, 194-200, DOI: 10.1021/jp109547w

Once again, into the breach…

Ess, Liu, and De Proft offer another analysis of the protobranching effect.¹ As a reminder, Schleyer, Mo and Houk and coworkers argue that the reason why branched alkanes are more stable than linear ones is a stabilizing 1,3-interaction that they call protobranching.² This proposal has been met with both supporters and vigorous attacks – see these posts.

What is new here is a partitioning of the total DFT energy into three terms. The critical term is one based on the Weizäcker kinetic energy, which is defined as the integral of the gradient of the density squared divided by the density. They call this a “steric energy term”. The second term is the standard electrostatic term, and the last term, which really just picks up the slack, is a “fermionic quantum term”.

Using this partition, they examine a series of bond separation reactions involving alkanes with differing degrees of “protobranches”. The upshot is that the steric energy, which is destabilizing, is less in branched alkanes that linear ones. However, the fermionic quantum term essentially cancels this out, as branched alkanes, being more compact, are more destabilized by this fermionic effect than are linear alkanes. So, the only remaining term, electrostatics is responsible for the branched alkanes being more stable than linear alkanes.

This does not ultimately resolve the issue of whether the protobranching effect, as defined by Schleyer, Mo and Houk, is real, but these authors purposely chose to avoid that question.

References

(1) Ess, D. H.; Liu, S.; De Proft, F., "Density Functional Steric Analysis of Linear and Branched Alkanes," J. Phys. Chem. A, 2010, ASAP, DOI: 10.1021/jp108577g

(2) Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K. N.; Schleyer, P. v. R., "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations," Chem. Eur. J. 2007, 13, 7731-7744, DOI: 10.1002/chem.200700602