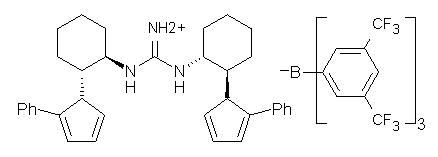
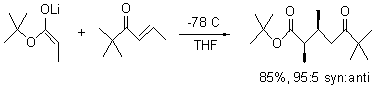
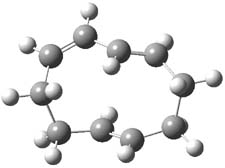
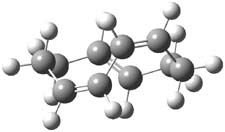
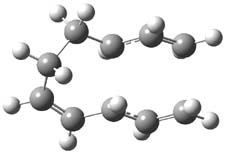
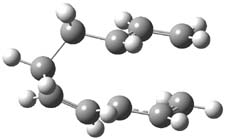
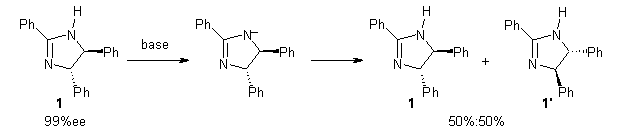
Jacobsen reports another interesting example of organocatalysis, here using a chiral guanadinium salt to catalyze the enantioselective Claisen rearrangement.¹ As an example, Reaction 1 proceeds in 6 days at 30 °C to give 81% yield with an ee of 84%. The system is also diastereoselective, so that Reaction 2, run for 6 days at 40 °C, gives an 82% yield with a diastereomeric ratio of 16:1 and an ee of 81%.

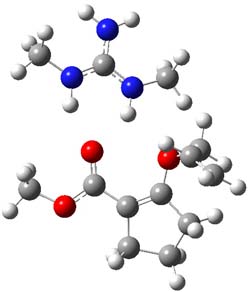
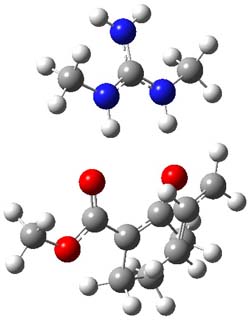
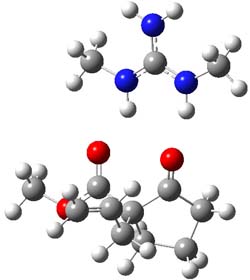
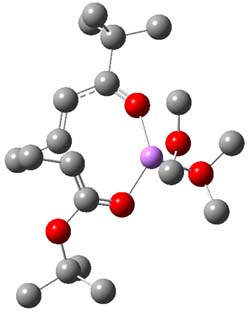
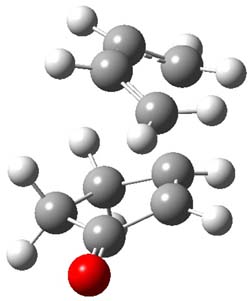
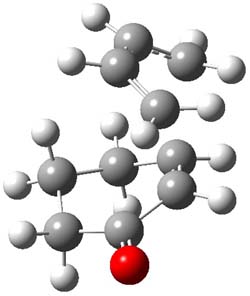
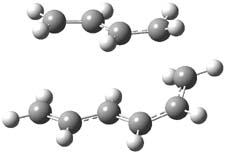
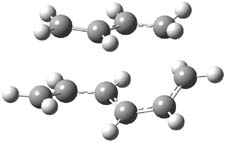
B3LYP/6-31G(d,p) computations provide some insight. The uncatalyzed reaction of 1 to give 2 is predicted to be exothermic by 16.1 kcal mol^-1, with an activation energy of 25.9 kcal mol^-1. Using N,N’-dimethylguanidnium as a model for the catalyst (and with no counter anion and no treatment of solvent – hexanes in this case), they find a complexation energy of almost 27 kcal mol^-1 for forming 3. 3 exhibits (See Figure 1) three hydrogen bond-like interactions – one N-H bifurcates to interact with the carbonyl oxygen and (a very long interaction) to the other oxygen. The product complex 4 also shows three hydrogen bond-like interactions, with an overall exothermicity of -14.7 kcal mol^-1. The complexed transition state 5 has two normal length hydrogen bonds, with an activation energy above 3 of 20.6 kcal mol^-1. Thus the complex lowers the barrier by about 5 kcal mol^-1, indicating the catalytic effect. They have not however addressed the enantioselectivity.

3	5
4

Figure 1. B3LYP/6-31G(d,p) optimized geometries of 3-5.

References

(1) Uyeda, C.; Rötheli, A. R.; Jacobsen, E. N., "Catalytic Enantioselective Claisen Rearrangements of O-Allyl β-Ketoesters," Angew. Chem. Int. Ed., 2010, 49, 9753–9756, DOI: 10.1002/anie.201005183

InChIs

1: InChI=1/C10H14O3/c1-3-7-13-9-6-4-5-8(9)10(11)12-2/h3H,1,4-7H2,2H3
InChIKey=NASFSRKGDOBHIX-UHFFFAOYAC

2: InChI=1/C10H14O3/c1-3-6-10(9(12)13-2)7-4-5-8(10)11/h3H,1,4-7H2,2H3/t10-/m0/s1
InChIKey=QXKXLNGEBVMWLH-JTQLQIEIBT

Mosey has a nice follow-up study on the origin of Woodward-Hoffman forbidden ring opening of cyclobutene under mechanical stress.¹ (See this blog post discussing the earlier work of Martinez.²) Pulling on cis substituents of a cyclobutene causes the ring to open in a disrotatory fashion. Normally, the WH forbidden pathway is accessed by photolysis which creates a new electronic state. Mosey asks if this same mechanism is occurring during mechanical stress.

On the face of things, this seems unlikely; how can a mechanical force lead to a new electronic state? CASSCF computations with either no applied external force or with varying sized external forces and IRC computations help answer this question. Without an external force, a diradical (or at least a species with high diradical character – and this could be the transition state) is found along the disrotatory pathway. This same diradical is found regardless of the size of the externally applied mechanical force. What does change is the position of the TS along the pathway: as the force increases, the TS becomes earlier, and the reaction barrier diminishes. No change in the electronic state is affected by the applied mechanical stress.

References

(1) Kochhar, G. S.; Bailey, A.; Mosey, N. J., "Competition between Orbitals and Stress in Mechanochemistry," Angew. Chem. Int. Ed., 2010, 49, 7452-7455, DOI: 10.1002/anie.201003978

(2) Ong, M. T.; Leiding, J.; Tao, H.; Virshup, A. M.; Martinez, T. J., "First Principles Dynamics and Minimum Energy Pathways for Mechanochemical Ring Opening of Cyclobutene," J. Am. Chem. Soc., 2009, 131, 6377-6379, DOI: 10.1021/ja8095834

Heathcock’s model for predicting the stereo-outcome of Michael additions¹ involves a metal bridging across the two carbonyl oxygens. For Reaction 1, the model predicts that 1,2-syn product over the 1,2-anti product based on more favorable steric arrangements in TSA relative to TSB. Note that other rotatamers of these TS models are possible, but are presumed to be less favorable due to the inability of the metal cation to bridge the carbonyls. In fact, the syn:trans ratio for Reaction 1 is 95:5.

Kwan and Evans have examined this (and related) reactions at the M05-2x/6-31G(d) level.² Dimethyl ether is used as the model for the solvent. The lowest energy transition state for Reaction 1 is TS1, shown in Figure 1 with suppressed drawing of the hydrogens (though the JMol active image will include the hydrogens). This structure is actually more like TSC, a rotamer that was thought to not have a bridging metal. TS1 does have the bridging metal, and this is accomplished by having dihedral values of 40° instead of the ideal 60°. So, computations support the general conclusion of the Heathcock approach, with a modification of the possible inclusion of some other rotamers, though the stereoprediction is not altered.

TS1

Figure 1. M05-2x/6-31G(d) optimized structure of the lowest energy transition state of Reaction 1. Hydrogens are removed in the image for clarity, but the Jmol active image (which you can see by clicking on the above image) will include the hydrogen atoms.

References

(1) Oare, D. A.; Heathcock, C. H. In Topics in Stereochemistry; Eliel, E. L., Wilen, S. H., Eds.; Wiley: New York, 1989; Vol. 19, p 227-408.

(2) Kwan, E. E.; Evans, D. A., "Intermolecular Michael Reactions: A Computational Investigation," Org. Lett. 2010, 12, 5124–5127, DOI: 10.1021/ol102017v

The proline-catalyzed aldol reaction is discussed in Chapter 5.3 of my book. This is an area of continued research and the recent paper of Sharma and Sunoj addresses an alternative mechanism involving oxazolidinone.¹ They examine the proline-catalyzed aldol self-condensation of propanal with B3LYP/6-31+G** and MP2/6-31+G** computations. This reaction is found to proceed² with 4:1 anti:syn diastereoselectivity.

An oxazolidinone intermediate has been observed in proline-catalyzed aldol condensations. This intermediate is proposed to come about via Path b, whereas the generally accepted mechanism put forth by Houk and List, discussed in my book, follows Path a. Sharma and Sunoj find that the oxazolidinone 7 is lower in energy than the enamine 4, and its barrier for ring opening back to 3 is large. Thus, it is not unreasonable that it is the observed intermediate.

Gas phase computations of the reaction of 4 to 5 predict a 99% ee and an anti:syn ratio of about 5:1, in nice agreement with experiment. However, incorporation of solvent reduces the ration to 2:1, and the MP2 computations give a ratio of 1.2:1, in even worse agreement with experiment. However, the major predicted product has the same absolute configuration as the observed product.

The other mechanism is examined in the key step 8 to 9. Here all computations predict that syn addition is favored over anti addition and the enantiomer of the experimentally observed product is predicted to be formed. In addition, intermediate 9 and the TSs leading to it are much higher in energy than intermediate 5 and the TSs associated with its formation. Thus, the oxazolidinone addition mechanism is discounted.

References

(1) Sharma, A.; Sunoj, R., "Enamine versus Oxazolidinone: What Controls Stereoselectivity in Proline-Catalyzed Asymmetric Aldol Reactions?," Angew. Chem. Int. Ed., 2010, 49, 6373-6377, DOI: 10.1002/anie.201001588

(2) Northrup, A. B.; MacMillan, D. W. C., "The First Direct and Enantioselective Cross-Aldol Reaction of Aldehydes," J. Am. Chem. Soc., 2002, 124, 6798-6799, DOI: 10.1021/ja0262378

The de novo design of catalysts for specific purposes remains an inspired goal for chemists and biochemists. Ken Houk and David Baker have been pursuing this goal, and their recent paper on the design of a catalyst for the bimolecular Diels-Alder¹ is a real significant step forward.

Their model enzyme is one that will provide a hydrogen bond acceptor to the carbamate proton of 1 and a proton donor to the carbonyl oxygen of the amide 2. This model is sketched in Figure 1. Glutamine or asparagines will serve as the acceptor and serine, threonine, or tyrosine will serve as the proton donor. The catalytic site is then modeled, and then this active site is fit within 207 protein scaffolds. About 10¹⁹ active site configurations are reduced to about 10⁶ possible protein scaffolds. Optimization of these led to 84 protein designs.

Figure 1. Enzyme model

These 84 possible proteins were then synthesized within E. coli and then tested for catalytic behavior
in the Diels-Alder reaction of 1 + 2. Only 2 enzymes have activity, and with some protein modifications, quite reasonable enzyme activity is found. These enzymes show strong selectivity for the substrates – addition of a methyl group significantly diminishes catalytic activity. Perhaps most important is that of the 8 possible isomers that can be formed (4 isomers are produced in the uncatalyzed reaction) only 1 is produced here, the 3R,4S isomer 3.

All-in-all, a quite remarkable accomplishment!

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D.,
"Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239.

InChIs

1: InChI=1/C13H13NO4/c1-2-3-8-14-13(17)18-9-10-4-6-11(7-5-10)12(15)16/h2-8H,1,9H2,(H,14,17)(H,15,16)/p-1/b8-3+/fC13H12NO4/h14H/q-1
InChIKey=HGMJQUSLRHRARW-OSXKDGDFDJ

2: InChI=1/C5H9NO/c1-4-5(7)6(2)3/h4H,1H2,2-3H3
InChIKey=YLGYACDQVQQZSW-UHFFFAOYAD

3: InChI=1/C18H22N2O5/c1-20(2)16(21)14-5-3-4-6-15(14)19-18(24)25-11-12-7-9-13(10-8-12)17(22)23/h4,6-10,14-15H,3,5,11H2,1-2H3,(H,19,24)(H,22,23)/p-1/t14-,15+/m0/s1/fC18H21N2O5/h19H/q-1
InChIKey=WWWDBAXWGWLFSD-AFFTYDCXDH

Li and Danishefsky report a study of the Diels-Alder reaction involving cyclobutenone 1 as the dienophile.¹ They claim that “perhaps the ring strain of 1 might well serve to enhance its dienophilicity relative to corresponding cyclopentenones or cyclohexenones.” In fact, 1 is an excellent dienophile, with reactions at or below 0° being accomplished in less than half a day with yields upwards of 90%. The reaction goes with endo selectivity.

What is surprising to me is the statement in the article:

While the magnitude of the effect could not have been predicted in advance, the rate enhancement with 1 must reflect the favorable effects of rehybridization of two particularly strained sp² carbons in the cycloaddition transition state.

Now, Danishefsky alludes to upcoming computations results in a future paper, but I don’t see why the rate enhancement could not have been “predicted in advance”. So, I have optimized the structures of reactants, endo and exo transition states, and products of the reaction of 1,3-butadiene with 1, cyclopentenone 2 and cyclohexenone 3 at B3LYP/6-311G(d) – Reactions 1-3.

The endo TS is preferred for the reaction of 1 and 2, while the endo and exo TSs for 3 are essentially isoenergetic. The optimized geometries are shown in Figure 1.

1TSendo

2TSendo

3TSendo

Figure 1. B3LYP/6-311G(d) optimized geometries of the endo TSs of Reactions 1-3.

The computed activation barriers and overall reaction energies are listed in Table 1. Clearly, the cycloaddition of 1 is favored both in terms of kinetics (having the lowest barrier) and thermodynamically (having the most exothermic reaction energy). In fact, the reaction barriers increases in going from 1 to 2 to 3 and the exothermicity decreases in that same order. This nicely dovetails with the strain energies of the dienophiles and the fact that cyclopententones and cyclohexenones are generally poor dienophiles. Thus, one clearly could have predicted these results in advance!

Table 1. Activation and Reaction Energy (kcal mol^-1) for Reactions 1-3.

Nonetheless, the experimental work is extremely nice and this work offers a new avenue into some interesting bicyclic structures.

Note: This post has been modified to correct the errors in the product structures and their associated InChIs and InChIKeys.

References

(1) Li, X.; Danishefsky, S. J., "Cyclobutenone as a Highly Reactive Dienophile: Expanding Upon Diels-Alder Paradigms," J. Am. Chem. Soc., 2010, 132, 11004-11005, DOI: 10.1021/ja1056888

InChIs

1: InChI=1/C4H4O/c5-4-2-1-3-4/h1-2H,3H2
InChIKey=DFLRGCFWSRELEL-UHFFFAOYAP

1prod: InChI=1/C8H10O/c9-8-5-6-3-1-2-4-7(6)8/h1-2,6-7H,3-5H2/t6-,7-/m0/s1
InChIKey=AYXQRXAAJYZWJJ-BQBZGAKWBC

2: InChI=1/C5H6O/c6-5-3-1-2-4-5/h1,3H,2,4H2
InChIKey=BZKFMUIJRXWWQK-UHFFFAOYAH

2prod: InChI=1/C9H12O/c10-9-6-5-7-3-1-2-4-8(7)9/h1-2,7-8H,3-6H2/t7-,8-/m0/s1
InChIKey=LOJATDUUSCWAOA-YUMQZZPRBU

3: InChI=1/C6H8O/c7-6-4-2-1-3-5-6/h2,4H,1,3,5H2
InChIKey=FWFSEYBSWVRWGL-UHFFFAOYAT

3prod: InChI=1/C10H14O/c11-10-7-3-5-8-4-1-2-6-9(8)10/h1-2,8-9H,3-7H2/t8-,9-/m0/s1
InChIKey=LFDGSLNQYSSFGI-IUCAKERBBQ

Alder and co-workers have published a substantial theoretical study of potential [6+4]-cycloaddition reactions.¹ There is much too much to summarize from this study, but I highlight here an interesting result that is consistent with one of the themes of the book and blog: unusual potential energy surfaces.

They examined two [6+4]-cycloadditon routes involving 1,3,5-hexatriene with 1,3-butadiene to give 1 and 2. These products are shown in Figure 1. A competing [4+2]-cycloaddition is also possible, giving rise to 3 and 4. Interestingly, only one TS is found leading to 1/3 and one TS leading to 2/4. (These TSs are also shown in Figure 1.) This is reminiscent of many examples from the book and blog where a single TS seems to lead to 2 different products. A valley-ridge inflection point divides the surface between 1 and 3 (VRI-1), and a second valley-ridge inflection point separates 2 from 4 (VRI-2). In addition a Cope transition state (CTS1) takes 1 into 3, and a second TS (CTS2) takes 2 into 4.

TS1	TS2
1	2
CTS1	CTS2

Figure 1. B3LYP/6-31G* optimized structures of the TSs and products of the reaction of 1,3,5-hexadiene with 1,3-butadiene.¹

This type of surface requires study of the dynamics to truly predict what the outcome will be of the reaction. Unfortunately, the low barriers for the Cope rearrangements along with 3 and 4 being much more stable than 1 and 2 indicates that the [6+4] product is unlikely to be observed. Nonetheless, this is yet another example of an unexpected PES.

References

(1) Alder, R. W.; Harvey, J. N.; Lloyd-Jones, G. C.; Oliva, J. M., "Can _π6 + _π4 = 10? Exploring Cycloaddition Routes to Highly Unsaturated 10-Membered Rings," J. Am. Chem. Soc. 2010, 132, 8325-8337, DOI: 10.1021/ja1008135

InChIs

1: InChI=1/C10H14/c1-2-4-6-8-10-9-7-5-3-1/h1-4,9-10H,5-8H2/b3-1-,4-2+,10-9+
InChIKey=RBGHZLIWLPEVLM-OCXPBMDHBA

2: InChI=1/C10H14/c1-2-4-6-8-10-9-7-5-3-1/h1-4,9-10H,5-8H2/b3-1-,4-2-,10-9+
InChIKey=RBGHZLIWLPEVLM-ARMDLRMMBD

3: InChI=1/C10H14/c1-3-9-7-5-6-8-10(9)4-2/h3-5,7,9-10H,1-2,6,8H2/t9-,10-/m0/s1
InChIKey=ANOQDGNLTWJTRB-UWVGGRQHBI

4: InChI=1/C10H14/c1-3-9-7-5-6-8-10(9)4-2/h3-5,7,9-10H,1-2,6,8H2/t9-,10+/m1/s1
InChIKey=ANOQDGNLTWJTRB-ZJUUUORDBZ

Grinberg and colleagues have published a combination of VCD and computation to understand the racemization of imidazoline 1 when exposed to base.¹ Experimental VCD performed at various temperatures indicates first-order kinetics with a barrier of about 24 kcal mol^-1.

The mechanism for this racemization was proposed and supported with B3LYP/6-31G(d) computations. The anion of 1 can undergo a disrotatory ring opening to form 2, passing through TS1 with a barrier of about 21 kcal mol^-1. Since 2 is chiral with the phenyl groups oriented in non-equivalent positions, ring closure of 2 will go back to 1 and not on to its racemate. In order to racemize, 2 must convert to 3, which can invert to 3’ and then on to 1’. While the barrier for ring opening is likely to be rate limiting, and it does match up reasonably well with the experimental value, the authors have not optimized the transition state that take 2 into 3 or the TS that interconverts 3 with 3’. It’s the former TS that may be pretty large as it requires disruption of the conjugation. Unfortunately, not only have the authors not computed these other TSs, the supplementary materials include only the optimized structure of 1 and not TS1, 2, or 3!

The authors do note that the ring opening is facilitated by the phenyl group on the chiral carbons of 1. They replaced the phenyls with cyclohexyl or cyclohexenyl groups and racemization is no longer observed. Strangely, the authors include in the supporting materials the optimized structures of these variants, but not the TSs for ring opening. Thus, the confirming evidence of a very high barrier for ring opening that would really nail down the mechanism is missing!

References

1) Ma, S.; Busacca, C. A.; Fandrick, K. R.; Bartholomeyzik, T.; Haddad, N.; Shen, S.; Lee, H.; Saha, A.; Yee, N.; Senanayake, C.; Grinberg, N., "Directly Probing the Racemization of Imidazolines by Vibrational Circular Dichroism: Kinetics and Mechanism," Org. Lett., 2010, 12, 2782–2785, DOI: 10.1021/ol100734t

InChIs

1: InChI=1/C21H18N2/c1-4-10-16(11-5-1)19-20(17-12-6-2-7-13-17)23-21(22-19)18-14-8-3-9-15-18/h1-15,19-20H,(H,22,23)/t19-,20-/m0/s1/f/h22H
InChIKey=UCCFUHZMGXEALP-RLNNBPQHDR

A couple of years ago Ess and Houk described computations on the cycloaddition reactions of ethene and ethyne with 9 different 1,3-dipoles 1-9.^1,2 Two interesting results were noted: (a) though barrier heights systematically decreased with the decreasing HOMO-LUMO gap of the 1,3-dipole, the reaction barriers are the same for a given dipole with either ethane or ethyne; (b) The TS geometries about the ethane and ethyne fragments are similar, even though the reactions are quite different in overall reaction energies. This implies a violation of the Hammond Postulate.

Ess and Houk suggested that what dictated these reactions were the energies of distortion of the 1,3-dipole. This is the energy needed to distort the 1,3-dipole into its geometry in the TS. This is typically associated with the bending about the central atom, but rehybridization at the
terminal positions is also needed in many cases. A plot of the distortion energy against the activation barrier gives a line with an R² value of 0.97.

Now Braida, Hiberty and coworkers have employed valence bond computations to interpret these findings.³ The 1,3-dipoles are composed of three valence bond structures a, b and c (shown for 1 below). The last structure (c) is the one associated with the cycloaddition reaction, as it is set up for making the two new bonds at the terminal positions.

The coefficients associated with these VB structures are given in Table 1. It is readily apparent that the degree of diradical character varies considerably among these compounds. Furthermore, for each set of 1,3-dipoles, increasing diradical content correlates with a decreased activation barrier. They also note a strong correlation of decreasing energy needed to excite the ground state 1,3-dipole to the diradical structure (of either the ground state geometry or in the TS geometry) with decreasing activation barrier. Thus, they conclude that it is the diradical character of the 1,3-dipole that controls the reaction – greater diradical character translates into a lower barrier. They argues that the concerted reaction proceeds in two phases, the first phase is distortion of the 1,3-dipole to create sufficient diradical character, and a second phase where the new bonds are made to the dipolarophile, independent of just what that dipolarophile happens to be.

Table 1. Coefficients of the 3 valence bond structures a-c for the ground state 1,3-dipoles 1-9.

References

(1) Ess, D. H.; Houk, K. N., "Distortion/Interaction Energy Control of 1,3-Dipolar
Cycloaddition Reactivity," J. Am. Chem. Soc., 2007, 129, 10646-10647, DOI: 10.1021/ja0734086

(2) Ess, D. H.; Houk, K. N., "Theory of 1,3-Dipolar Cycloadditions: Distortion/Interaction and Frontier Molecular Orbital Models," J. Am. Chem. Soc., 2008, 130, 10187-10198, DOI: 10.1021/ja800009z

(3) Braida, B.; Walter, C.; Engels, B.; Hiberty, P. C., "A Clear Correlation between the Diradical Character of 1,3-Dipoles and Their Reactivity toward Ethylene or Acetylene," J. Am. Chem. Soc., 2010, 132, 7631-7637, DOI: 10.1021/ja100512d

InChIs

1: InChI=1/N2O/c1-2-3
InChIKey=GQPLMRYTRLFLPF-UHFFFAOYAP

2: InChI=1/HN3/c1-3-2/h1H
InChIKey=JUINSXZKUKVTMD-UHFFFAOYAO

3: InChI=1/CH2N2/c1-3-2/h1H2
InChIKey=YXHKONLOYHBTNS-UHFFFAOYAZ

4: InChI=1/CHNO/c1-2-3/h1H
InChIKey=UXKUODQYLDZXDL-UHFFFAOYAL

5: InChI=1/CH2N2/c1-3-2/h1-2H
InChIKey=XILSUYCQFZFDIK-UHFFFAOYAR

6: InChI=1/C2H3N/c1-3-2/h1H,2H2
InChIKey=LSOWAYXKGAQDOG-UHFFFAOYAI

7: InChIInChIKey=DITLKQKHWHCNBT-UHFFFAOYAB

8: InChI=1/CH4N2/c1-3-2/h2-3H,1H2
InChIKey=SSRHHPGUPLMOHA-UHFFFAOYAA

9: InChI=1/C2H5N/c1-3-2/h3H,1-2H2
InChIKey=DASBPRRGHQBNKH-UHFFFAOYAE

Duncan has discovered a pseudopericyclic [3,3]-sigmatropic rearrangement, ¹ and what is particularly interesting is how rare this seems to be! (See this post for an earlier related study.) Using CASSCF/6-31G* computations of Reactions 1-9, only Reaction 1 is found to be pseudopericyclic. (The transition state for this reaction is shown in Figure 1). This characterization is based largely on the shapes of the active MOs, one of which displays two orbital disconnections. In addition, this transition state is much more planar than is typical for a [3,3]-rearrangement. Dihedral angles are about 20 ° in the TS for reaction 1, while in the other reaction TSs, their dihedral angless are about 50 ° or even larger. This is consistent with Birney’s contention that pseudopericyclic reactions have nearly planar TSs. The activation barrier for Reaction 1 is also quite small, 19.4 kcal mol^-1, much lower than for Reactions 2 (26.2 kcal mol^-1) and 3 (33.1 kcal mol^-1).

Figure 1. CASSCF/6-31G* optimized TS for Reaction 1.

References

(1) Forte, L.; Lafortune, M. C.; Bierzynski, I. R.; Duncan, J. A., "CASSCF Molecular Orbital Calculations Reveal a Purely Pseudopericyclic Mechanism for a [3,3] Sigmatropic Rearrangement," J. Am. Chem. Soc., 2010, 132, 2196-2201, DOI: 10.1021/ja906679g

InChIs

Reaction 1:
Reactant (2-(2-methanimidoylcyclopropyl)ethenone):
InChI=1/C6H7NO/c7-4-6-3-5(6)1-2-8/h1,4-7H,3H2
InChIKey=FMPHPBIFFKHFNF-UHFFFAOYAG
Product (1,4-dihydroazepin-7-one):
InChI=1/C6H7NO/c8-6-4-2-1-3-5-7-6/h2-5H,1H2,(H,7,8)/f/h7H
InChIKey=BEYCJMUGQZWVBC-QDQILVOLCK