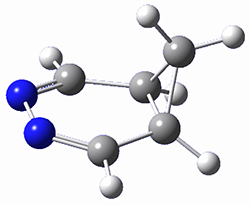
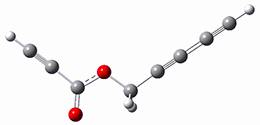
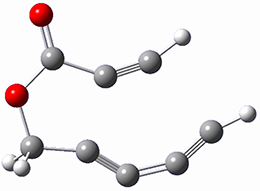
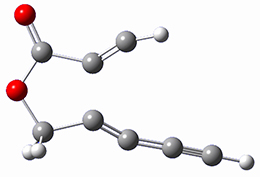
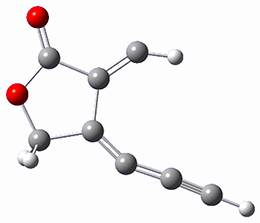
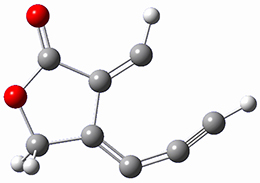
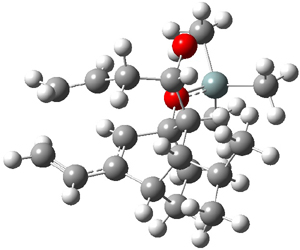
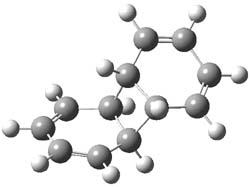
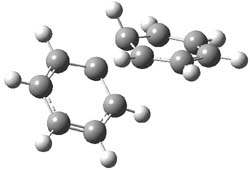
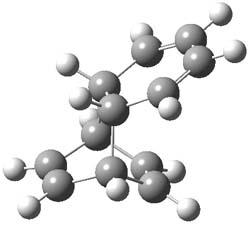
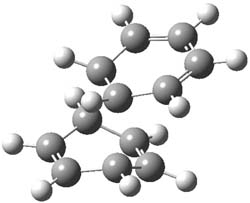
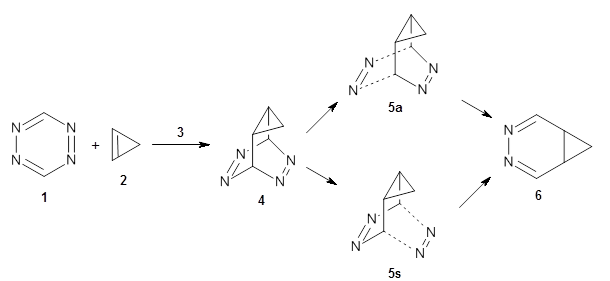
Houk and Doubleday report yet another example of dynamic effects in reactions that appear to be simple, ordinary organic reactions.¹ Here they look at the Diels-Alder reaction of tetrazine 1 with cyclopropene 2. The reaction proceeds by first crossing the Diels-Alder transition state 3 to form the intermediate 4. This intermediate can then lose the anti or syn N₂, through 5a or 5s, to form the product 6. The structures and relative energies, computed at M06-2X/6-31G(d), of these species are shown in Figure 1.

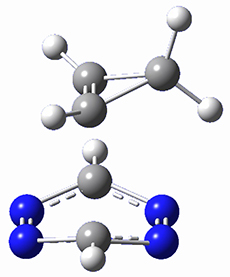
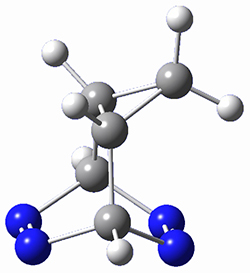
3 17.4	4 -33.2
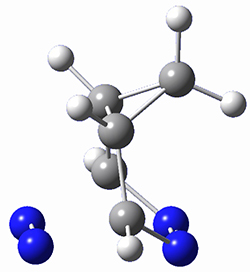
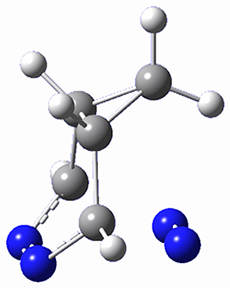
5a -28.9	5s -20.0
6 -86.2

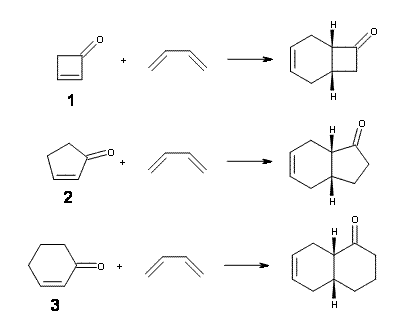
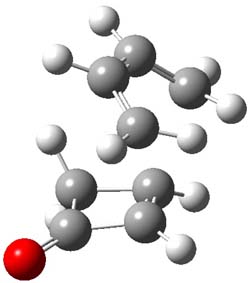
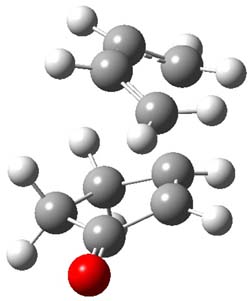
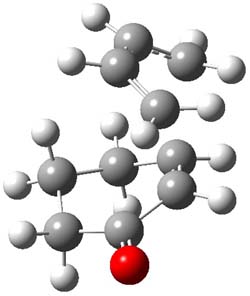
Figure 1. M06-2X/6-31G(d) optimized geometries and energies (relative to 1 + 2) of the critical points along the reaction of tetrazine with cyclopropene.

The large difference in the activation barriers between crossing 5a and 5s (nearly 9 kcal mol^-1) suggests, by transition state theory, a preference of more than a million for loss of the anti N₂ over the syn N₂. However, quasiclassical trajectory studies, using B3LYP/6-31G(d), finds a different situation. The anti pathway is preferred, but only by a 4:1 ratio! This dynamic effect arises from a coupling of the v₃ mode which involves a rocking of the cyclopropane ring that brings a proton near the syn N₂ functionality, promoting its ejection. In addition, the trajectory studies find short residence times within the intermediate neighborhood for the trajectories that lead to the anti product and longer residence times for the trajectories that lead to the syn product. All together, a very nice example of dynamic effects playing a significant role in a seemingly straightforward organic reaction.

References

(1) Törk, L.; Jiménez-Osés, G.; Doubleday, C.; Liu, F.; Houk, K. N. "Molecular Dynamics of the Diels–Alder Reactions of Tetrazines with Alkenes and N₂ Extrusions from Adducts," J. Am. Chem. Soc. 2015, 137, 4749-4758, DOI: 10.1021/jacs.5b00014.

InChIs

1: InChI=1S/C2H2N4/c1-3-5-2-6-4-1/h1-2H
InChIKey=HTJMXYRLEDBSLT-UHFFFAOYSA-N

2: InChI=1S/C3H4/c1-2-3-1/h1-2H,3H2
InChIKey=OOXWYYGXTJLWHA-UHFFFAOYSA-N

4: InChI=1S/C5H6N4/c1-2-3(1)5-8-6-4(2)7-9-5/h2-5H,1H2
InChIKey=JGSMBFYJCNPYDM-UHFFFAOYSA-N

6: InChI=1S/C5H6N2/c1-4-2-6-7-3-5(1)4/h2-5H,1H2
InChIKey=RYJFHKGQZKUXEH-UHFFFAOYSA-N

Cramer, Hoye, Kuwata and coworkers have examined the intramolecular cyclization of an alkyne with a diyne.¹ Their model system is 1, which can cyclize through a concerted transition state TSC togive the benzyne product 2, or it can proceed through a stepwise pathway, first going through TS1 to form the intermediate INT¸ before traversing through a second transition state TS2 and on to product 2. Using both computations and experiments, they examined a series of compounds with
differing substituents at the ends of the two yne moieties.

The experiments show almost the exact same rate of reaction regardless of the terminal substituents. This includes the parent case where the terminal substituents are hydrogens and also the case where the terminal substituents (which end up on adjacent centers on the benzyne ring) are bulky TMS groups. And though there is no real rate effect due to changes in solvent or the presence of light or triplet oxygen, which suggest a concerted reaction, these substituent effects argue for a step wise reaction.

SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p)
computations help explain these observations. Shown in Figure 1 are the optimized geometries and relative energies of the critical points on the reaction surface for the conversion of 1 into 2, and these results are similar with the other substituents as well.

1 (0.0)	2 (-56.9)
TSC (31.5)
TS1 (25.5)	INT (18.8)
TS2 (18.1)

Figure 1. SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p) optimized geometries and relative energies (kcal mol^-1).

The first thing to note is that the concerted TSC is higher in energy than the stepwise TS1. The wavefunction for TSC unstable towards moving from a restricted to unrestricted formalism. Reoptimization of some of these concerted TSs actually led to the stepwise TS.

The next item of note is that TS2 for this case is actually lower in energy than the intermediate (this is a true TS on the energy surface, but when zero-point energy and other thermal corrections are included, it becomes lower in energy than INT). For some of the cases the second TS lies above the intermediate, but typically by a small amount.

Therefore, the mechanism of this reaction is stepwise, but the second step might have such a small barrier (or even no barrier) that one might consider this to be concerted, though highly asymmetric and really bearing little resemblance to more traditional concerted pericyclic reactions.

The authors obliquely hinted at some potential interesting dynamics. I suspect that molecular dynamics calculations will show no effect of that second TS, and one might observe some interesting dynamics, which could be seen in kinetic isotope experiments.

References

(1)  Marell, D. J.; Furan, L. R.; Woods, B. P.; Lei, X.; Bendelsmith, A. J.; Cramer, C. J.; Hoye, T. R.; Kuwata, K. T. "Mechanism of the Intramolecular Hexadehydro-Diels–Alder Reaction," J. Org. Chem. 2015 ASAP, DOI: 10.1021/acs.joc.5b01356.

InChIs

1: InChI=1S/C8H4O2/c1-3-5-6-7-10-8(9)4-2/h1-2H,7H2
InChIKey=MGXDIFXPYGGQLF-UHFFFAOYSA-N

2: InChI=1S/C8H4O2/c9-8-7-4-2-1-3-6(7)5-10-8/h2,4H,5H2
InChIKey=MYFORDRJCVOBTH-UHFFFAOYSA-N

Diels-Alder reaction involving fullerenes have been known for some time. They occur across the [6,6] double bond of C₆₀, the one between two fused 6-member rings. Houk and Briseno report on the Diels-Alder reaction of C₆₀ with pentacene 1 and bistetracene 2 and compare their computations with experiments.¹

Pentacene and bistetracene ring numbering convention

Computations were performed for the reaction of 1 and 2 with C₆₀ at M06-2x/6-31G(d)//M062x-3-21G*. The reaction can occur with the dienophile being either ring 1, 2, or 3 of pentacene and ring 1, 2, 3, or 4 of bistetracene. They located TSs and products for all of these possibilities. Select TSs and products are shown in Figure 1.

For the reaction of 1a, the lowest energy TS is for the reaction at the central ring (ring 3), and the resulting product is the lowest energy product. The transition state (PT_TS3) is shown in Figure 1. This TS has the least distortion energy of the three possibilities, because reacting at this central ring destroys the least amount of aromaticity of pentacene. For the reaction of 1b, the lowest barrier is again for reaction of ring 3 (through TMSPT_TS3). However, the product from the reaction with ring 2 (TMSPT_P2) is lower in free energy than TMSPT­_P3, likely caused by steric interactions with the silyl substituents. This actually matches up with experiments which indicate that an analogue of TMSPT_P2 is the kinetic product but TMSPT_P3 is the thermodynamic product.

PT_TS3
TMSPT_­TS3
TMSPT_P2	TMSPT_P3
BT_TS2	BT_P2

Figure 1. M06-2x/3-21G* optimized geometries.
(Once again a reminder that clicking on any of these structures will launch JMol and you’ll be able to visualize and manipulate this structure in 3-D.)

The computations involving the Diels-Alder reaction of C₆₀ with either 2a or 2b come to the same conclusion. In both cases, the lowest barrier is for the reaction at ring 2, and the product of the reaction at this same ring is the only one that is endoergonic. The geometries of BT_TS2 and BT_P2 are shown in Figure 1. More importantly, the barrier for the Diels-Alder reaction involving 2a and 2b are at least 6 kcal mol^-1 higher than the barriers for the reaction of 1a and 1b, in complete agreement with experiments that show little reaction involving analogues of 2b with C₆₀, while analogues of 1b are reasonably rapid.

References

(1) Cao, Y.; Liang, Y.; Zhang, L.; Osuna, S.; Hoyt, A.-L. M.; Briseno, A. L.; Houk, K. N. "Why Bistetracenes Are Much Less Reactive Than Pentacenes in Diels–Alder Reactions with Fullerenes," J. Am. Chem. Soc. 2014, 136, 10743-10751, DOI: 10.1021/ja505240e.

Halskov, et al.¹ reported the interesting Diels-Alder selectivity shown in Scheme 1. The linear trienamine 1 did not undergo the Diels-Alder addition, while the less stable cross-conjugated diene 2 does react with 3 with high diastereo- and enantioselectivity. Their MPW1K/6-31+G(d,p) computations on a model system, carried out for a gas-phase environment, indicated a concerted mechanism, with thermodynamic control. However, the barrier for the reverse reaction for the kinetic product was computed to be greater than 30 kcal mol^-1, casting doubt on the possibility of thermodynamic control.

Scheme 1.

Houk and co-workers² have re-examined this reaction with the critical addition of performing the computation including the solvent effects. Since the stepwise alternatives involve the formation of zwitterions, solvent can be critical in stabilizing these charge-separated species, intermediates that might be unstable in the gas phase. Henry Rzepa has pointed out in his blog and on many comments in this blog about the need to include solvent, and this case is a prime example of the problems inherent in neglecting solvation.

Using models of the above reaction Houk located two zwitterionic intermediates of the Michael addition for both the reactions of 4 with 6 and of 5 with 6. The second step then involves the closure of the ring to give what would be Diels-Alder products. This is shown in Scheme 2. They were unable to locate transition states for any concerted pathways. The computations were done at M06-2x/def2-TZVPP/IEFPCM//B97D/6-31+G(d,p)/IEFPCM, modeling trichloromethane as the solvent.

Scheme 2. Numbers in italics are energies relative to 4 + 6.

The activation barrier for the second step in each reaction is very small, typically less than 5 kcal mol^-1, so the first step is rate determining. The lowest barrier is for the reaction of 5 leading to 9, analogous to the observed product. Furthermore, 9 is also the thermodynamic product. Thus, the regioselectivity is both kinetically and thermodynamically controlled through a stepwise reaction. This conclusion is only possible by including solvent in order to stabilize the zwitterionic intermediates, and should be a word of caution for everyone doing computations: be sure to include solvent for any reactions that involved charged or charge-separated species at any point along the reaction pathway!

References

(1) Halskov, K. S.; Johansen, T. K.; Davis, R. L.; Steurer, M.; Jensen, F.; Jørgensen, K. A. "Cross-trienamines in Asymmetric Organocatalysis," J. Am. Chem. Soc. 2012, 134, 12943-12946,
DOI: 10.1021/ja3068269.

(2) Dieckmann, A.; Breugst, M.; Houk, K. N. "Zwitterions and Unobserved Intermediates in Organocatalytic Diels–Alder Reactions of Linear and Cross-Conjugated Trienamines," J. Am. Chem. Soc. 2013, 135, 3237-3242, DOI: 10.1021/ja312043g.

The intramolecular Diels-Alder reaction of 1 occurs slowly, but quantitatively, at room temperature.¹ This is unusual as most Diels-Alder cyclizations require heating to typically 200 °C. For example, the related cyclization of 2 requires heating to 170 °C.² What is the cause for this proximity-induced reaction?

Houk and Baran address this question using a computational approach.³ The Diels-Alder reaction of 2 and a simplified analogue of 1, namely 3, were computed at CPCM/M06-2x/6-311+G(d,p)//B3LYP/6-31G(d). The optimized transition states for the reaction of 2 and 3 are shown in Figure 1. The free energy of activation of 3 is 5.4 kcal mol^-1 lower in energy than the free energy of activation of 2. This is consistent with the much faster reaction of 1 than 2 observed in the experiment.

TS2

TS3

Figure 1. B3LYP/6-31G(d) for the transition states of Reactions 2 and 3.

Partitioning 3 into fragments allows Houk and Baran to apply the distortion model. They find that the rigid diene in 3 (and thereby 1) accelerates the reaction relative to the more flexible diene of 2. Further, strain relief in going from 3 (and thereby 1) to TS3 (and thereby to TS of reaction 1) and the formation of an intramolecular hydrogen bond leads to the lower activation energy of 3, and therefore of 1.

References

(1) Maimone, T. J.; Voica, A.-F.; Baran, P. S. "A Concise Approach to Vinigrol," Angew. Chem. Int. Ed. 2008, 47, 3054-3056, DOI: 10.1002/anie.200800167.

(2) Diedrich, M. K.; Klärner, F.-G.; Beno, B. R.; Houk, K. N.; Senderowitz, H.; Still, W. C. "Experimental Determination of the Activation Parameters and Stereoselectivities of the Intramolecular Diels−Alder Reactions of 1,3,8-Nonatriene, 1,3,9-Decatriene, and 1,3,10-Undecatriene and Transition State Modeling with the Monte Carlo-Jumping Between Wells/Molecular Dynamics Method," J. Am. Chem. Soc. 1997, 119, 10255-10259, DOI: 10.1021/ja9643331.

(3) Krenske, E. H.; Perry, E. W.; Jerome, S. V.; Maimone, T. J.; Baran, P. S.; Houk, K. N. "Why a Proximity-Induced Diels–Alder Reaction Is So Fast," Org. Lett. 2012, 14, 3016-3019, DOI: 10.1021/ol301083q.

InChIs

1: InChI=1S/C23H40O2Si/c1-10-12-19(24)21-20(16(3)4)18-13-14-23(21,15-17(18)11-2)25-26(8,9)22(5,6)7/h10-11,15-16,18-21,24H,1-2,12-14H2,3-9H3/t18?,19-,20?,21?,23+/m0/s1
InChIKey=NGVNTJGCNDZDEY-RHDCMTSYSA-N

2: InChI=1S/C10H16/c1-3-5-7-9-10-8-6-4-2/h3-5,7H,1-2,6,8-10H2/b7-5+
InChIKey=HXZJJSYHNPCGKW-FNORWQNLSA-N

3: InChI=1S/C20H34O2Si/c1-8-10-18(21)20(15(3)4)14-17-11-12-19(20,13-16(17)9-2)22-23(5,6)7/h8-9,13,15,17-18,21H,1-2,10-12,14H2,3-7H3/t17?,18-,19+,20?/m0/s1
InChIKey=GDQHAOHEZAJKPI-FUFFSDJGSA-N

Has there been an organic reaction more examined by computational methods than the Diels-Alder reaction? You’d think we would have covered all aspects of this reaction by now, but no, it appears that this reaction remains fertile hunting grounds.

Doubleday and Houk have examined the Diels-Alder reaction with an eye towards its synchronicity,¹ an area that Houk has delved into throughout his career. While most experiments show significant stereoselectivity, a few examples display a small amount of stereo loss. Computed transition states tend to have forming C-C bond distances that are similar, though with proper asymmetric substitution, the asymmetry of the TS can be substantial. In this paper,¹ they utilize reaction dynamics specifically to assess the time differential between the formation of the two new C-C single bonds. They examined the eight reactions shown below. The first six (R1-R6) have symmetric transition states, though with the random sampling about the TS for the initial condition of the trajectories, a majority of asymmetric starting conditions are used. The last two (R7 and R8) reactions have asymmetric TSs and the random sampling amplifies this asymmetry.

Nonetheless, the results of the dynamics are striking. The time gap, the average time between the formations of the first and second new C-C bond, for R1-R6 is less than 5 fs, much shorter than a C-C vibration. These reactions must be considered as concerted and synchronous. Even the last two reactions (R7 and R8), which are inherently more asymmetric, still have very short time gaps of 15 and 56 fs, respectively. One might therefore reasonably conclude that they too are concerted and synchronous.

There are some exceptions – a few trajectories in the last two reactions involve a long-lived (~1000 fs) diradical intermediate. At very high temperature, about 2% of the trajectories invoke a diradical intermediate. But the overall message is clear: the Diels-Alder reaction is inherently concerted and synchronous.

References

(1) Black, K.; Liu, P.; Xu, L.; Doubleday, C.; Houk, K. N. "Dynamics, transition states, and timing of bond formation in Diels–Alder reactions," Proc. Nat. Acad. Sci. USA, 2012, 109, 12860-12865, DOI: 10.1073/pnas.1209316109

In a follow-up to their experimental study that found that cyclobutenone is an excellent dienophile (and which I blogged about here), Danishefsky teams up with Houk and provides an insight into the reactivity.¹ In the Diels-Alder reaction of cyclopentadiene with 2-cyclohexenone, 2-cyclopentenone and cyclobutenone, the product yield increases in the order 36%, 50% and 77%. M06-2x activation enthalpies decrease in this series 15.0, 13.3 and 10.5 kcal mol^-1.

While these activation energies do not correlate with reaction energies, the activation energies do correlate nicely with the distortion energy. (Distortion energy is the energy required to distort reactants to their geometries in the transition state, but without their interaction.) Houk and Danishefsky argue that it is much easier to distort cyclobutenone to its geometry in the TS (and this distortion is primarily moving the alkenyl hydrogens out of plane, away from the incoming diene) than for the larger rings. This is due to (a) the larger s-character of the C-H bond in the smaller ring and (b) the C-C-C angle in the smaller ring is closer to the angle in the pyramidalized TS structure.

References

(1) Paton, R. S.; Kim, S.; Ross, A. G.; Danishefsky, S. J.; Houk, K. N., "Experimental Diels–Alder Reactivities of Cycloalkenones and Cyclic Dienes Explained through Transition-State Distortion Energies," Angew. Chem. Int. Ed., 2011, 44, 10366–10368, DOI: 10.1002/anie.201103998

Bendikov and co-workers have examined the dimerization of linear acenes at M06-2x/6-31G(d).¹ They have looked at the formal forbidden [4+4] reaction that takes, for example, 2 molecules of benzene into three possible dimer products 1P_anti1-2, 1P_syn1-2, and 1P_syn1-4. The relative energies of these products increases in that order, and all three are much higher in energy than reactants; the lowest energy dimer is 1P_anti1-2, lying 47.4 kcal mol^-1 above two benzene molecules. Similarly, the dimerization of naphthalene is also endothermic, but the formation of the symmetric dimer of anthracene 3P-2,2’ is exothermic by 5.4 kcal mol^-1. This gibes nicely with the best estimate of -9 ± 3 kcal mol^-1.² Dimerization of the higher acenes are increasingly exothermic.

The transition state for the dimerization of benzene is concerted, though very asymmetric, as seen in Figure 1. Its energy is quite high (77.79 kcal mol^-1) and so this reaction can be completely discounted. The TS for the dimerization of naphthalene is also concerted and asymmetric, but the reaction pathway for the dimerization is stepwise, with a diradical intermediate. Furthermore, the highest barrier for this stepwise reaction is 33.3 kcal mol^-1. The activation energy of the back reaction (anthracene dimer to two anthrecene molecules) was measured 36.3 kcal mol^-1,³ and the computed barrier of 38.7 kcal mol^-1 is in nice agreement. The computed barriers for the dimerization of the higher acenes are predicted to be even lower than that of anthracene, consistent with the observation of dimers of these molecules.

1Panti1-2	1TSanti1-2
1P-42	1TS-42

Figure 1. M06-2x /6-31G(d) optimized structures.

I was curious that the authors did not consider the formally allowed [4+2] dimerization, leading for example to 1P-42. So, I optimized this product and the concerted transition state leading to it. These are shown in Figure 1. The barrier through this transition state is still very large (54.1 kcal mol^-1) but it is 23 kcal mol^-1 lower in energy than the barrier of the [4+4] reaction! The Product of the [4+2] is also lower in energy (by 9 kcal mol^-1) than 1P_anti1-2. It seems to me that this type of dimerization is worth examining too – though I must say I have not as yet looked to see if anyone has explored this already.

References

(1) Zade, S. S.; Zamoshchik, N.; Reddy, A. R.; Fridman-Marueli, G.; Sheberla, D.; Bendikov,
M., "Products and Mechanism of Acene Dimerization. A Computational Study," J. Am. Chem. Soc., 2011, 133, 10803-10816, DOI: 10.1021/ja106594v

(2) Grimme, S.; Diedrich, C.; Korth, M., "The Importance of Inter- and Intramolecular van der Waals Interactions in Organic Reactions: the Dimerization of Anthracene Revisited," Angew. Chem. Int. Ed., 2006, 45, 625-629, DOI: 10.1002/anie.200502440

(3) Greene, F. D., "Problems of stereochemistry in photochemical reactions in the anthracene area," Bull. Soc. Chim. Fr., 1960, 1356-1360

InChIs

Benzene: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H
InChIKey=UHOVQNZJYSORNB-UHFFFAOYAH

1P_anti1-2: InChI=1/C12H12/c1-2-6-10-9(5-1)11-7-3-4-8-12(10)11/h1-12H
InChIKey=WMPWOGVJEXSFLI-UHFFFAOYAP

1P_syn1-2: InChI=1/C12H12/c1-2-6-10-9(5-1)11-7-3-4-8-12(10)11/h1-12H
InChIKey=WMPWOGVJEXSFLI-UHFFFAOYAP

1P_syn1-4: InChI=1/C12H12/c1-2-10-4-3-9(1)11-5-7-12(10)8-6-11/h1-12H
InChIKey=BCBHEUOKKNYIAT-UHFFFAOYAI

1P-42: InChI=1/C12H12/c1-2-4-12-10-7-5-9(6-8-10)11(12)3-1/h1-12H
InChIKey=ONVDJSCNMCYFTI-UHFFFAOYAY

Anthracene: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H
InChIKey=MWPLVEDNUUSJAV-UHFFFAOYAK

3P-2,2’: InChI=1/C28H20/c1-2-10-18-17(9-1)25-19-11-3-4-12-20(19)26(18)28-23-15-7-5-13-21(23)27(25)22-14-6-8-16-24(22)28/h1-16,25-28H
InChIKey=JUTIJVADGQDBGY-UHFFFAOYAY

The de novo design of catalysts for specific purposes remains an inspired goal for chemists and biochemists. Ken Houk and David Baker have been pursuing this goal, and their recent paper on the design of a catalyst for the bimolecular Diels-Alder¹ is a real significant step forward.

Their model enzyme is one that will provide a hydrogen bond acceptor to the carbamate proton of 1 and a proton donor to the carbonyl oxygen of the amide 2. This model is sketched in Figure 1. Glutamine or asparagines will serve as the acceptor and serine, threonine, or tyrosine will serve as the proton donor. The catalytic site is then modeled, and then this active site is fit within 207 protein scaffolds. About 10¹⁹ active site configurations are reduced to about 10⁶ possible protein scaffolds. Optimization of these led to 84 protein designs.

Figure 1. Enzyme model

These 84 possible proteins were then synthesized within E. coli and then tested for catalytic behavior
in the Diels-Alder reaction of 1 + 2. Only 2 enzymes have activity, and with some protein modifications, quite reasonable enzyme activity is found. These enzymes show strong selectivity for the substrates – addition of a methyl group significantly diminishes catalytic activity. Perhaps most important is that of the 8 possible isomers that can be formed (4 isomers are produced in the uncatalyzed reaction) only 1 is produced here, the 3R,4S isomer 3.

All-in-all, a quite remarkable accomplishment!

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D.,
"Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239.

InChIs

1: InChI=1/C13H13NO4/c1-2-3-8-14-13(17)18-9-10-4-6-11(7-5-10)12(15)16/h2-8H,1,9H2,(H,14,17)(H,15,16)/p-1/b8-3+/fC13H12NO4/h14H/q-1
InChIKey=HGMJQUSLRHRARW-OSXKDGDFDJ

2: InChI=1/C5H9NO/c1-4-5(7)6(2)3/h4H,1H2,2-3H3
InChIKey=YLGYACDQVQQZSW-UHFFFAOYAD

3: InChI=1/C18H22N2O5/c1-20(2)16(21)14-5-3-4-6-15(14)19-18(24)25-11-12-7-9-13(10-8-12)17(22)23/h4,6-10,14-15H,3,5,11H2,1-2H3,(H,19,24)(H,22,23)/p-1/t14-,15+/m0/s1/fC18H21N2O5/h19H/q-1
InChIKey=WWWDBAXWGWLFSD-AFFTYDCXDH

Li and Danishefsky report a study of the Diels-Alder reaction involving cyclobutenone 1 as the dienophile.¹ They claim that “perhaps the ring strain of 1 might well serve to enhance its dienophilicity relative to corresponding cyclopentenones or cyclohexenones.” In fact, 1 is an excellent dienophile, with reactions at or below 0° being accomplished in less than half a day with yields upwards of 90%. The reaction goes with endo selectivity.

What is surprising to me is the statement in the article:

While the magnitude of the effect could not have been predicted in advance, the rate enhancement with 1 must reflect the favorable effects of rehybridization of two particularly strained sp² carbons in the cycloaddition transition state.

Now, Danishefsky alludes to upcoming computations results in a future paper, but I don’t see why the rate enhancement could not have been “predicted in advance”. So, I have optimized the structures of reactants, endo and exo transition states, and products of the reaction of 1,3-butadiene with 1, cyclopentenone 2 and cyclohexenone 3 at B3LYP/6-311G(d) – Reactions 1-3.

The endo TS is preferred for the reaction of 1 and 2, while the endo and exo TSs for 3 are essentially isoenergetic. The optimized geometries are shown in Figure 1.

1TSendo

2TSendo

3TSendo

Figure 1. B3LYP/6-311G(d) optimized geometries of the endo TSs of Reactions 1-3.

The computed activation barriers and overall reaction energies are listed in Table 1. Clearly, the cycloaddition of 1 is favored both in terms of kinetics (having the lowest barrier) and thermodynamically (having the most exothermic reaction energy). In fact, the reaction barriers increases in going from 1 to 2 to 3 and the exothermicity decreases in that same order. This nicely dovetails with the strain energies of the dienophiles and the fact that cyclopententones and cyclohexenones are generally poor dienophiles. Thus, one clearly could have predicted these results in advance!

Table 1. Activation and Reaction Energy (kcal mol^-1) for Reactions 1-3.

Nonetheless, the experimental work is extremely nice and this work offers a new avenue into some interesting bicyclic structures.

Note: This post has been modified to correct the errors in the product structures and their associated InChIs and InChIKeys.

References

(1) Li, X.; Danishefsky, S. J., "Cyclobutenone as a Highly Reactive Dienophile: Expanding Upon Diels-Alder Paradigms," J. Am. Chem. Soc., 2010, 132, 11004-11005, DOI: 10.1021/ja1056888

InChIs

1: InChI=1/C4H4O/c5-4-2-1-3-4/h1-2H,3H2
InChIKey=DFLRGCFWSRELEL-UHFFFAOYAP

1prod: InChI=1/C8H10O/c9-8-5-6-3-1-2-4-7(6)8/h1-2,6-7H,3-5H2/t6-,7-/m0/s1
InChIKey=AYXQRXAAJYZWJJ-BQBZGAKWBC

2: InChI=1/C5H6O/c6-5-3-1-2-4-5/h1,3H,2,4H2
InChIKey=BZKFMUIJRXWWQK-UHFFFAOYAH

2prod: InChI=1/C9H12O/c10-9-6-5-7-3-1-2-4-8(7)9/h1-2,7-8H,3-6H2/t7-,8-/m0/s1
InChIKey=LOJATDUUSCWAOA-YUMQZZPRBU

3: InChI=1/C6H8O/c7-6-4-2-1-3-5-6/h2,4H,1,3,5H2
InChIKey=FWFSEYBSWVRWGL-UHFFFAOYAT

3prod: InChI=1/C10H14O/c11-10-7-3-5-8-4-1-2-6-9(8)10/h1-2,8-9H,3-7H2/t8-,9-/m0/s1
InChIKey=LFDGSLNQYSSFGI-IUCAKERBBQ