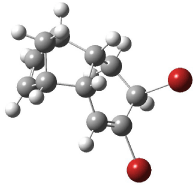
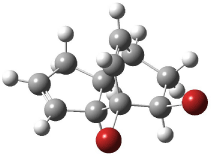
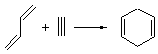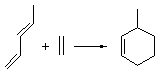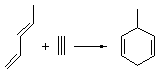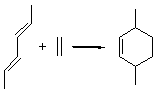Dynamic effects rear up yet again in a seemingly simple reaction. Singleton has examined the Diels-Alder cycloaddition of acrolein with methyl vinyl ketone to give two cross products 1 and 2.¹ Upon heating the product mixture, 1 is essentially the only observed species. The retro-Diels-Alder is much slower than the conversion of 2 into 1. Using a variety of rate data, the best estimate for the relative formation of 1:2 is 2.5.

The eight possible transition states for this reaction were computed with a variety of methodologies, all providing very similar results. The lowest energy TS is TS3. A TS of type TS4 could not be found; all attempts to optimize it collapsed to TS3.

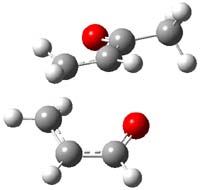
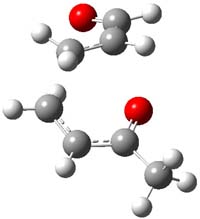
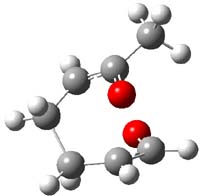
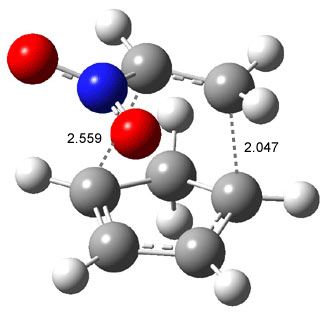
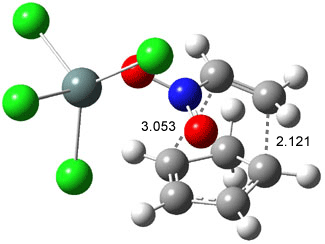
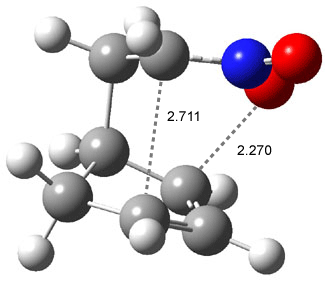
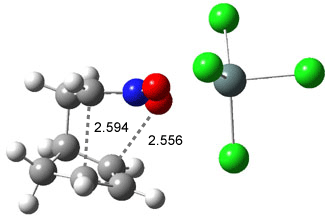
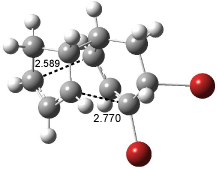
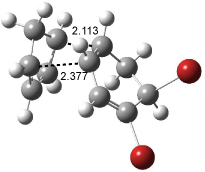
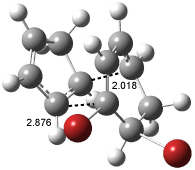
IRC computations indicate the TS3 leads to 1. The lowest energy TS that leads to 2 is TS6, but a second TS (TS5) lower in energy than TS6 also leads to 1. The other TS are still higher in energy. A Cope-type TS that interconverts 1 and 2 (TS7) was also located. The geometries of these TSs are shown in Figure 1.

TS3 (0.0)	TS5 (4.2)
TS6 (5.2)	TS7 (-0.4)

Figure 1. MP2/6-311+G** optimized geometries and relative energies (kcal mol^-1) of TS3-TS7.¹

Ordinary transition state theory cannot explain the experimental results – the energy difference between the lowest barrier to 1 (TS3) and to 2 (TS6) suggests a rate preference of over 700:1 for 1:2. But the shape of the potential energy surface is reminiscent of others that have been discussed in both my book (Chapter 7) and this blog (see my posts on dynamics) – a surface where trajectories cross a single TS but then bifurcate into two product wells.

To address the chemical selectivity on a surface like this, one must resort to molecular dynamics and examine trajectories. In their MD study of the 296 trajectories that begin at TS3 with motion towards product, 89 end at 1 and 33 end at 2, an amazingly good reproduction of experimental results! Interestingly, 174 trajectories recross the transition state and head back towards reactants. These recrossing trajectories result from “bouncing off” the potential energy wall of the forming C₄-C₅ bond.

In previous work, selectivity in on these types of surfaces was argued in terms of which well the TS was closer to. But analysis of the trajectories in this case revealed that a strong correlation exists between the initial direction and velocity in the 98 cm^-1 vibration – the vibration that corresponds to the closing of the second σ bond, the one between C₆-O₁ (forming 1), in the negative direction, and closing the C­₃-O₈ bond (forming 2) in the positive direction. Singleton argues that this is a type of dynamic matching, and it might be more prevalent that previously recognized.

References

(1) Wang, Z.; Hirschi, J. S.; Singleton, D. A., "Recrossing and Dynamic Matching Effects on Selectivity in a Diels-Alder Reaction," Angew. Chem. Int. Ed., 2009, 48, 9156-9159, DOI: 10.1002/anie.200903293

InChIs

1: InChI=1/C7H10O2/c1-6(8)7-4-2-3-5-9-7/h3,5,7H,2,4H2,1H3
InChIKey=AOFHZPHBPUYLAG-UHFFFAOYAJ

2: InChI=1/C7H10O2/c1-6-3-2-4-7(5-8)9-6/h3,5,7H,2,4H2,1H3
InChIKey=PLZQHPPETMMEED-UHFFFAOYAD

Organic catalysis is a major topic of Chapter 5 of my book. The use of iminium ions as a catalyst and to provide stereoselection, pioneered by MacMillan,¹ was not discussed in the book.

Macmillan had proposed that the iminium 2 formed of imidazolinone 1 and (E)-3-phenylprop-2-enal has conformation A. This conformation blocks access to one face of the alkene and directs, for example, dienophiles to the opposite face. Houk found that conformer B is lower in energy at B3LYP/6-31G(d).²

Now Tomkinson³ has produced a study that convincingly shows that 2 exists as conformer B. An x-ray structure shows this conformation in the solid state. Proton NMR shows that the methyl group signals are interpretable only as coming from B. Finally, SCS-MP2/aug-cc-pVTZ//BHandH/6-31+G(d,p) (see Figure 1) computations show that B is 1.2 kcal mol^-1 more stable than A in the gas phase, and PCM computations indicate that this gap is reduced by less then 0.5 kcal mol^-1 in methanol or acetonitrile.

Conformation B provides little steric hindrance at the β-carbon of the iminium ion, explaining its poor stereoselectivity in conjugate additions.

A

B

Figure 1. BHandH/6-31+G(d,p) optimized structures of conformers A and B of 2.

References

(1) Ahrendt, K. A.; Borths, C. J.; MacMillan, D. W. C., "New Strategies for Organic Catalysis: The First Highly Enantioselective Organocatalytic Diels-Alder Reaction," J. Am. Chem. Soc., 2000, 122, 4243-4244, DOI: 10.1021/ja000092s.

(2) Gordillo, R.; Houk, K. N., "Origins of Stereoselectivity in Diels-Alder Cycloadditions Catalyzed by Chiral Imidazolidinones," J. Am. Chem. Soc., 2006, 128, 3543-3553, DOI: 10.1021/ja0525859.

(3) Brazier, J. B.; Evans, G.; Gibbs, T. J. K.; Coles, S. J.; Hursthouse, M. B.; Platts,
J. A.; Tomkinson, N. C. O., "Solution Phase, Solid State, and Theoretical Investigations on the MacMillan Imidazolidinone," Org. Lett., 2009, 11, 133-136, DOI: 10.1021/ol802512y.

InChIs

1: InChI=1/C13H18N2O/c1-13(2)14-11(12(16)15(13)3)9-10-7-5-4-6-8-10/h4-8,11,14H,9H2,1-3H3/t11-/m0/s1
InChIKey=UACYWOJLWBDSHG-NSHDSACABQ

2: InChI=1/C22H25N2O/c1-22(2)23(3)21(25)20(17-19-13-8-5-9-14-19)24(22)16-10-15-18-11-6-4-7-12-18/h4-16,20H,17H2,1-3H3/q+1/b15-10+,24-16+/t20-/m0/s1
InChIKey=ZPEHVNACGWTABV-BYFMJTDEBT

Concern about the use of DFT for general use in organic chemistry remains high; see my previous posts (1, 2, 3). Houk has now examined the reaction enthalpies of ten simple Diels-Alder reactions using a variety of functionals in the search for the root cause of the problem(s).¹

The ten reactions are listed in Scheme 1, and involve cyclic and acyclic dienes and either ethylene or acetylene as the dienophile. Table 1 lists the minimum and maximum deviation of the DFT enthalpies relative to the CBS-QB3 enthalpies (which are in excellent accord with experiment). Clearly, all of the DFT methods perform poorly, with significant errors in these simple reaction energies. The exception is the MO6-2X functional, whose errors are only slightly larger than that found with the SCS-MP2 method. Use of a larger basis set (6-311+G(2df,2p)) reduced errors only a small amount.

Table 1. Maximum, minimum and mean deviation of reaction enthalpies (kcal mol^-1) for the reactions in Scheme 1 using the 6-31+G(d,p) basis set.¹

In order to discern where the problem originates, they next explore the changes that occur in the Diels-Alder reaction: two π bonds are transformed into one σ and one π bond and the conjugation of the diene is lost, leading to (proto)branching in the product. Reactions 1-3 are used to assess the energy consequence of converting a π bond into a σ bond, creating a protobranch, and the loss of conjugation, respectively.

The energies of these reactions were then evaluated with the various functionals. It is only with the conversion of the π bond into a σ bond that they find a significant discrepancy between the DFT estimates and the CBS-QB3 estimate. DFT methods overestimate the energy for the π → σ exchange, by typically around 5 kcal mol^-1, but it can be much worse. Relying on cancellation of errors to save the day for DFT will not work when these types of bond changes are involved. Once again, the user of DFT is severely cautioned!

References

(1) Pieniazek, S. N.; Clemente, F. R.; Houk, K. N., "Sources of Error in DFT Computations of C-C Bond Formation Thermochemistries: π → σ Transformations and Error Cancellation by DFT Methods," Angew. Chem. Int. Ed. 2008, 47, 7746-7749, DOI: 10.1002/anie.200801843

Jorgensen reports an enhanced QM/MM and ab initio study of the rate enhancement of Diels-Alder reactions in various solvents.¹ This study extends earlier studies that he and others have done, many of which are discussed in Chapter 6.2 of the book. In this study, he reports QM/MM computations using the PDDG/PM3 method for the QM component, and MP2 computations incorporating CPCM to account for bulk solvent effects.

The major advance in methodology in this paper is performing a two-dimensional potential of mean force analysis where these two dimensions correspond to the forming C-C distances. In addition, computations were done for water, methanol, acetonitrile and hexane as solvents. Highlights of the results are listed in Table 1.

Table 1. Computed bond asynchronicity^a and activation energy^b (kcal/mol) for the Diels-Alder reaction with cyclopentadiene.

The semi-empirical method underestimates the asynchronicity of these gas-phase Diels-Alder TSs. However, with inclusion of the solvent, the computations do indicate a growing asynchronicity with solvent polarity, This is associated with the ability of the solvent, especially protic solvents, to preferentially hydrogen bond to the carbonyl in the TS.

In terms of energetics, in must first be pointed out that the computations dramatically overestimate the activation barriers. However, the relative trends are reproduced: the barrier increases from water to methanol to acetonitrile to hexane. Jorgensen also computed the activation barriers at MP2/6-311+G(2d,p) with CPCM using the CBS=QB3 gas phase geometries. Some of these results are listed in Table 2. The results for water are in outstanding agreement with experiment. However, the results for the other solvents are poor, underestimating the increase in barrier in moving to the more polar solvent.

Table 2. MP2/6-311+G(2d,p)/CPCM values for ΔG^‡ (kcal/mol).

Bottom line, the conclusions of this study are in agreement with the earlier studies, namely that the hydrophobic effect (better may be the enforced hydrophobic interaction) and greater hydrogen bonding in the TS (both more and stronger hydrogen bonds) account for the rate acceleration of the Diels-Alder reaction in water.

References

(1) Acevedo, O.; Jorgensen, W. L., "Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theory Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.

The search for unusual potential energy surface topologies continues. Unusual surfaces can lead to dynamic effects that result in rates and product distributions dramatically divergent from that predicted by statistical theories. I addressed this topic in Chapter 7 of the book.

Houk has found another interesting example in the Diels-Alder reaction of cyclopentadiene with nitrostyrene 1.¹ The [4+2] adduct is 2, which can undergo a [3,3] Cope-like rearrangement to give 3. Product 3 can also result from a [2+4] Diels-Alder cycloaddition where cyclopentadiene acts as the dienophile.

Like some of the examples in Chapter 7, the potential energy surface, computed at B3LYP/6-31+G*, contains a single transition state (TS1) from reactants. Continuing on the reaction path past the transition state, a valley ridge inflection point (VRI) intervenes, causing the path to bifurcate: one path leads to 2 and the other leads to 3. In other words, a single transition state leads to two different products! TS1 is geometrically closer to 2 than 3, while TS2 lies closer to 3 than 2 (Figure 1). This topology directs most molecules to traverse a path over TS1 and on to 2. What is novel in this paper is that the acid-catalyzed reaction, using SnCl₄, shifts TS1 towards 3 and TS2 towards 2, leading to the opposite product distribution. The uncatalyzed reaction favors formation of 2 while the catalyzed reaction favors 3 over 2. Confirmation of this prediction awaits a molecular dynamics study.

TS1	TS1-Cat
TS2	TS2-Cat

Figure 1. B3LYP/6-31+G(d) optimized structures for TS1 and TS2.¹

References

(1) Celebi-Olcum, N.; Ess, D. H.; Aviyente, V.; Houk, K. N., “Lewis Acid Catalysis Alters the Shapes and Products of Bis-Pericyclic Diels-Alder Transition States,” J. Am. Chem. Soc., 2007, 129, 4528-4529. DOI: 10.1021/ja070686w

InChI

1: InChI=1/C8H7NO2/c10-9(11)7-6-8-4-2-1-3-5-8/h1-7H/b7-6+
2: InChI=1/C13H13NO2/c15-14(16)13-11-7-6-10(8-11)12(13)9-4-2-1-3-5-9/h1-7,10-13H,8H2
3: InChI=1/C13H13NO2/c15-14-9-12(10-5-2-1-3-6-10)11-7-4-8-13(11)16-14/h1-6,8-9,11-13H,7H2

Here as an interesting, relatively straightforward example of how modern computational methods can help elucidate a reaction mechanism. Brinker¹ examined the thermolysis of (1S,2R,5R,7S,8R)-4,5-dibromotricyclo[6.2.1.0^2,7]undeca-3,9-diene 1. The observed products were cyclopentadiene (and its dimer), bromobenzene and (1R,2S,6S,7R,10R)-1,10-dibromotricyclo[5.2.2.0^2,6]undeca-3,8-diene
2. They proposed two possible mechanisms to account for these products. In the first mechanism, 1 can convert to 2 via a Cope rearrangement (path a, Scheme 1). The alternative mechanism has 1 undergo a retro-Diels-Alder reaction to produce 1,6-dibromo-1,3-cyclohexadiene 3 and cyclopentadiene 4 (path b, Scheme 1) 3 can then lose HBR to give bromobenzene. But more interesting is the possibility that cyclopentadiene and 3 can undergo a Diels-Alder reaction (path c, Scheme 1), but one with role reversal, i.e. cylopentadiene acts as the dienophile here, rather than the diene component as in the reverse of path b. This second Diels-Alder reaction (path c) produces 2.

Scheme 1

Brinker optimized the structures in Scheme 1, along with the transition states from paths a-c, at B3LYP/6-31G(d). These structures are shown in Figure 1 and their relative energies are listed in Table 1. The Cope rearrangement is favored over the retro-Diels-Alder by 3.6 kcal mol^-1. While the subsequent Diels-Alder step (path c) has a low electronic barrier (21.7 kcal mol^-1), it is enthalpically disfavored and the free energy barrier is high (40.4 kcal mol^-1. Thus, formation of 2 derives mostly from the direct Cope rearrangement of 2. Production of bromobenzene from 2 results from the retro-Diels-Alder (path b) followed by loss of HBr.

Table 1. Electronic and Free Energies (kcal mol^-1­) computed at B3LYP/6-31G(d).¹

1 xyz file	2 xyz files
TS(a) xyz files	TS(b) xyz file
TS(c) xyz file

Figure 1. B3LYP/6-31G(d) optimized structures.¹

InChI:

1: InChI=1/C11H12Br2/c12-10-4-8-6-1-2-7(3-6)9(8)5-11(10)13/h1-2,4,6-9,11H,3,5H2/t6-,7+,8-,9+,11-/m1/s1

2: InChI=1/C11H12Br2/c12-10-6-7-4-5-11(10,13)9-3-1-2-8(7)9/h1,3-5,7-10H,2,6H2/t7-,8+,9+,10+,11+/m0/s1

References

(1) Su, K. J.; Mieusset, J. L.; Arion, V. B.; Brecker, L.; Brinker, U. H., “Cope Rearrangement versus a Novel Tandem Retro-Diels-Alder-Diels-Alder Reaction with Role reversal,” Org. Lett. 2007, 9, 113-115, DOI: 10.1021/ol0626793