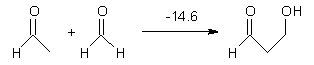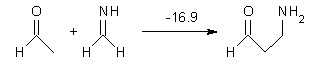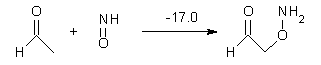For those of you interested in learning about dispersion corrections for density functional theory, I recommend Grimme’s latest review article.¹ He discusses four different approaches to dealing with dispersion: (a) vdW-DF methods whereby a non-local dispersion term is included explicitly in the functional, (b) parameterized functional which account for some dispersion (like the M06-2x functional), (c) semiclassical corrections, labeled typically as DFT-D, which add an atom-pair term that typically has an r^-6 form, and (d) one-electron corrections.

The heart of the review is the comparison of the effect of including dispersion on thermochemistry. Grimme nicely points out that reaction energies and activation barriers typically are predicted with errors of 6-8 kcal mol^-1 with conventional DFT, and these errors are reduced by up to 1.5 kcal mol^-1 with the inclusion fo the “-D3” correction. Even double hybrid methods, whose mean errors are much smaller (about 3 kcal mol^-1), can be improved by over 0.5 kcal mol^-1 with the inclusion of the “-D3” correction. The same is also true for conformational energies.

Since the added expense of including the “-D3” correction is small, there is really no good reason for not including it routinely in all types of computations.

(As an aside, the article cited here is available for free through the end of this year. This new journal WIREs Computational Molecular Science has many review articles that will be of interest to readers of this blog.)

References

(1) Grimme, S., "Density functional theory with London dispersion corrections," WIREs Comput. Mol. Sci., 2011, 1, 211-228, DOI: 10.1002/wcms.30

Another remarkable piece of science from the Schreiner and Allen groups has appeared demonstrating the critical importance of combining experiment with computations.¹ (This one will surely be in the running for computational chemistry paper of the year.) Once again they examine tunneling from a carbene intermediate, but this time with an amazing conclusion that will have impact on chemistry textbooks!

Schreiner and Allen have previously examined a number of hydroxycarbenes (see these posts: A, B, C) and have found tunneling to be the main exit channel from these carbenes. The tunneling passes through barriers that are as large as 30 kcal mol^-1, and as expected, the deuterium labeled analogues have tunneling half lives that are exceptionally long, like 4000 years.

Now they examine methylhydroxycarbene 1,¹ which is interesting because there are two possible exit channels, leading to acetaldehyde 2 or vinyl alcohol 3. Previous gas-phase pyrolysis of pyruvic acid suggested the intermediacy of 1, which rearranges to 2 much more rapidly than to 3. However, G1 computations predict the barrier to 3 is smaller than the barrier to 2,² which should mean that 2 is the kinetic product!

Methylhydroxycarbene 1 was prepared by flash pyrolysis of pyruvic acid with capture of the products in an argon matrix. The carbene 1 was characterized by IR. The predicted frequencies (CCSD(T)/cc-pCVTZ – with corrections for anharmonicity) of 9 of the 11 bands of 1 are within 8 cm^-1 of the experimental frequencies. The OH and OD stretches, the ones not in agreement, are likely to be perturbed by the matrix. The predicted (MRCC/aug-cc-pVTZ) and experimental UV spectrum are also in close agreement.

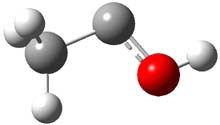
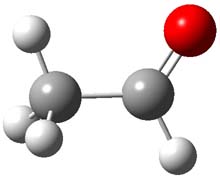
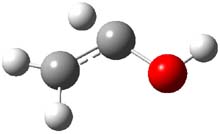
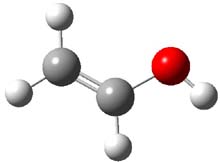
Holding the matrix at 11 K and following the spectra of 1-3 led to the following important kinetic results: the half-life for formation of 2 is 66 min with no 3 observed to form. In addition, the rate for the deuterium labeled carbene to form 2 was too long for measuring, but was 196 minutes in Kr and 251 minutes in Xe. CCSD(T)/cc-pCVCZ computations followed by focal point methods gives the barrier to form acetaldehyde from 1 as 28.0 kcal mol^-1 while that to form vinyl alcohol 3 is much lower: 22.6 kcal mol^-1. (The structures of these three molecules and the transition states connecting them are shown in Figure 1.) Apparently, the reaction passes through or over the higher barrier in large preference over passing through or over the lower barrier!

1
TS12	2
TS13	3

Figure 1. CCSD(T)/cc-pCVTZ optimizes structures of 1-3 and the transition states connecting 1 to 2 and 1 to 3.

Precise mapping of the intrinsic reaction path at CCSD(T)/cc-pCVTZ allows for computing the WKB tunneling probabilities. This leads to the prediction of the half-life for the reaction 1 → 2 as 71 minutes, in excellent agreement with experiment. The computed half-life for the deuterium labeled reaction of 400 years and the computed half-life for 1 → 3 of 190 days are both in fine agreement with experiment.

Why does the reaction preferentially tunnel through the higher barrier? Well, the tunneling rate is dependent on the square root of the barrier height and linearly on the barrier width. The width is much smaller for the rearrangement to 2. The hydrogen needs to move a shorter amount in proceeding from 1to 2 than to 3, and in the rearrangement to vinyl alcohol a second hydrogen must migrate downwards to form the planar vinyl group. Basically, width beats out the height.

The important conclusion from this paper is the following: in addition to reactions being under kinetic or thermodynamic control, we must now consider a third options – a reaction under tunneling control!

A nice perspective on this paper and its implications has been written by Carpenter, who points out how this adds to our general notion of significant limitations to transition state theory.³

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Ley, D.; Gerbig, D.; Wu, C.-H.; Allen, W. D., "Methylhydroxycarbene: Tunneling Control of a Chemical Reaction," Science, 2011, 332, 1300-1303, DOI: 10.1126/science.1203761.

(2) Smith, B. J.; Nguyen Minh, T.; Bouma, W. J.; Radom, L., "Unimolecular rearrangements connecting hydroxyethylidene (CH₃-C-OH), acetaldehyde (CH₃-CH:O), and vinyl alcohol (CH₂:CH-OH)," J. Am. Chem. Soc., 1991, 113, 6452-6458, DOI: 10.1021/ja00017a015

(3) Carpenter, B. K., “Taking the High Road and Getting There Before You,” Science, 2011, 332, 1269-1270, DOI: 10.1126/science.1206693.

InChIs

1: InChI=1/C2H4O/c1-2-3/h3H,1H3
InChIKey=JVKQHDUTAFISFX-UHFFFAOYAN

2: InChI=1/C2H4O/c1-2-3/h2H,1H3
InChIKey=IKHGUXGNUITLKF-UHFFFAOYAB

3: InChI=1/C2H4O/c1-2-3/h2-3H,1H2
InChIKey=IMROMDMJAWUWLK-UHFFFAOYAT

The much publicized failure of common DFT methods to accurately describe alkane isomer energy and bond separation reactions (which I have blogged about many times) has recently been attributed to long-range exchange¹ (see this post) or simply just DFT exchange² (see this post). Grimme now responds by emphatically claiming that it is a failure in accounting for medium-range electron correlation.³

First, Grimme notes that the bond separation energy for linear alkanes (as defined in
Reaction 1) is underestimated by HF, and slightly overestimated by MP2, but SCS-MP2 provides energy in nice agreement with CCSD(T)/CBS energies. Since MP2 adds in coulomb correlation to the HF energy (which treats exchange exactly within a one determinant wavefunction), the traditional wavefunction approach strongly suggests a correlation error.

CH₃(CH₂)_mCH₃ + mCH₄ → (m+1)CH₃CH₃        Reaction 1

Next, bond separation energies computed with PBE and BLYP (which lack exact exchange), PBE0 (which has 25% non-local exchange) and BHLYP (which has 50% non-local exchange) are all similar and systematically too small. So, exchange cannot be the culprit. It must be correlation.

He also makes two other interesting points. First, inclusion of a long-range correction – his recently proposed D3 method⁴ – significantly improves results, but the bond separation energies are still underestimated. It is only with the double-hybrid functional B2PLYP and B2GPPLYP that very good bond separation energies are obtained. And these methods do address the medium-range correlation issue. Lastly, Grimme notes that use of zero-point vibrational energy corrected values or enthalpies based on a single conformation are problematic, especially as the alkanes become large. Anharmonic corrections become critical as does inclusion of multiple conformations with increasing size of the molecules.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett., 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

(2) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys., 2009, DOI: 10.1039/b818412g.

(3) Grimme, S., "n-Alkane Isodesmic Reaction Energy Errors in Density Functional Theory Are Due to Electron Correlation Effects," Org. Lett. 2010, 12, 4670–4673, DOI: 10.1021/ol1016417

(4) Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H., "A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu," J. Chem. Phys., 2010, 132, 154104, DOI: 10.1063/1.3382344.

Computing anions have long been understood to offer interesting challenges. For example, anions require diffuse functions for reasonable description. Jensen¹ has now investigated the electron affinity of atoms and small molecules with three DFT methods: BHHLYP having 50% HF and 50% Becke exchange, B3LYP having 20% HF and 80% Becke exchange and BLYP with 100% Becke exchange. The result is that all three express varying degrees of electron loss from the atom or molecule in the anion. Thus the anionic species really possess only fractional anionic charge.

In cation-anion pairs or in large species that have strong electron acceptors and donors (say a protein), this electron loss manifests itself in less ionic character than what should actually be present. In other words density is erroneously moved off of the anionic center and transferred to the cationic center.

This error is due to poor description of the long-range exchange. Including the LC correction does eliminate the problem, and so one should be very careful in using DFT for anions.

References

(1) Jensen, F., "Describing Anions by Density Functional Theory: Fractional Electron Affinity," J. Chem. Theory Comput., 2010, 6, 2726-2735, DOI: 10.1021/ct1003324

What procedure should one employ when trying to determine a chemical structure from an NMR spectrum? I have discussed a number of such examples in the past, most recently the procedure by Goodman for dealing with the situation where one has the experimental spectra of 2 diastereomers and you are trying to identify the structures of this pair.¹ Now, Goodman provides an extension for the situation where you have a single experimental NMR spectrum and you are trying to determine which of a number of diasteromeric structures best accounts for this spectrum.² Not only does this prescription provide a means for identifying the best structure, it also provides a confidence level.

The method, called DP4, works as follows. First, perform an MM conformational search of every diastereomer. Select the conformations within 10 kJ of the global minimum and compute the ¹³C and ¹H NMR chemical shifts at B3LYP/6->31G(d,p) – note no reoptimizations! Then compute the Boltzmann weighted average chemical shift. Scale these shifts against the experimental values. You’re now ready to apply the DP4 method. Compute the error in each chemical shift. Determine the probability of this error using the Student’s t test (with mean, standard deviation, and degrees of freedom as found using their database of over 1700 ¹³C and over 1700 ¹H chemical shifts). Lastly, the DP4 probability is computed as the product of these probabilities divided by the sum of the product of the probabilities over all possible diastereomers. This process is not particularly difficult and Goodman provides a Java applet to perform the DP4 computation for you!

In the paper Smith and Goodman demonstrate that in identifying structures for a broad range of natural products, the DP4 method does an outstanding job at identifying the correct diastereomer, and an even better job of not misidentifying a wrong structure to the spectrum. Performance is markedly better than the typical procedures used, like using the correlation coefficient or mean absolute error. I would strongly encourage those people utilizing computed NMR spectra for identifying chemical structures to considering employing the DP4 method – the computational method is not particularly computer-intensive and the quality of the results is truly impressive.

Afternote: David Bradley has a nice post on this paper, including some comments from Goodman.

References

(1) Smith, S. G.; Goodman, J. M., "Assigning the Stereochemistry of Pairs of Diastereoisomers Using GIAO NMR Shift Calculation," J. Org. Chem., 2009, 74, 4597-4607, DOI: 10.1021/jo900408d

(2) Smith, S. G.; Goodman, J. M., "Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability," J. Am. Chem. Soc., 2010, 132, 12946-12959, DOI: 10.1021/ja105035r

Here’s one more attempt to discern the failure of DFT to handle simple alkanes (see this earlier post for a previous attempt to answer this question). Tsuneda and co-workers¹ have employed long-range corrected (LC) DFT to the problem of the energy associated with “protobranching”, i.e., from the reaction

CH₃(CH₂)­_nCH₃ + n CH₄ → (n+1) CH₃CH₃

They computed the energy of this reaction for the normal alkanes propane through decane using a variety of functionals, and compared these computed values with experimentally-derived energies. Table 1 gives the mean unsigned error for a few of the functionals. The prefix “LC” indicated inclusion of long-range corrections, “LCgau” indicates the LC scheme with a gaussian attenuation, and “LRD” indicates inclusion of long-range dispersion.

Table 1. Mean unsigned errors of the “protobranching”
reaction energy of various functional compared to experiment.

A number of important conclusions can be drawn. First, with both LC and LRD very nice agreement with experiment can be had. If only LC is included, the error increases on average by over 1 kcal mol^-1. The MO6-2x functional, touted as a fix of the problem, does not provide complete correction, though it is vastly superior to B3LYP and other hybrid functionals. The authors conclude that the need for LC incorporation points out that the exchange functional lacks the ability to account for this effect. Medium-range correlation is not the main source of the problem as large discrepancies in the reaction energy error occur when different functionals are used that are corrected for LC and LRD. Choice of functional still matters, but LC correction appears to be a main culprit and further studies of its addition to standard functionals would be most helpful.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett. 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

Houk has performed a very nice examination of the performance of some density functionals.¹ He takes a quite different approach than what was proposed by Grimme – the “mindless” benchmarking² using random molecules (see this post). Rather, Houk examined a series of simple aldol, Mannich and α-aminoxylation reactions, comparing their reaction energies predicted with DFT against that predicted with CBQ-QB3. The idea here is to benchmark DFT performance for simple reactions of specific interest to organic chemists. These reactions are of notable current interest due their involvement in organocatalytic enantioselective chemistry (see my posts on the aldol, Mannich, and Hajos-Parrish-Eder-Sauer-Wiechert reaction). Examples of the reactions studied (along with their enthalpies at CBS-QB3) are Reaction 1-3.

For the four simple aldol reactions and four simple Mannich reactions, PBE1PBE,
mPW1PW91 and MO6-2X all provided reaction enthalpies with errors of about 2 kcal mol^-1. The much maligned B3LYP functional, along with B3PW91 and B1B95 gave energies with significant larger errors. For the three α-aminoxylation reactions, the errors were better with B3PW91 and B1B95 than with PBE1PBE or MO6-2X. Once again, it appears that one is faced with finding the right functional for the reaction under consideration!

Of particular interest is the decomposition of these reactions into related isogyric, isodesmic
and homdesmic reactions. So for example Reaction 1 can be decomposed into Reactions 4-7 as shown in Scheme 1. (The careful reader might note that these decomposition reactions are isodesmic and homodesmotic and hyperhomodesmotic reactions.) The errors for Reactions 4-7 are typically greater than 4 kcal mol^-1 using B3LYP or B3PW91, and even with MO6-2X the errors are about 2 kcal mol^-1.

Scheme 1.

Houk also points out that Reactions 4, 8 and 9 (Scheme 2) focus on having similar bond changes as in Reactions 1-3. And it’s here that the results are most disappointing. The errors produced by all of the functionals for Reactions 4,8 and 9 are typically greater than 2 kcal mol^-1, and even MO2-6x can be in error by as much as 5 kcal mol^-1. It appears that the reasonable performance of the density functionals for the “real world” aldol and Mannich reactions relies on fortuitous cancellation of errors in the underlying reactions. Houk calls for the development of new functionals designed to deal with fundamental simple bond changing reactions, like the ones in Scheme 2.

Scheme 2

References

(1) Wheeler, S. E.; Moran, A.; Pieniazek, S. N.; Houk, K. N., "Accurate Reaction Enthalpies and Sources of Error in DFT Thermochemistry for Aldol, Mannich, and α-Aminoxylation Reactions," J. Phys. Chem. A 2009, 113, 10376-10384, DOI: 10.1021/jp9058565

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, 5, 993–1003, DOI: 10.1021/ct800511q

Predicting the pK_a of a compound from first principles remains a challenge, despite all of the many algorithmic and methodological advantages within the sphere of computational chemistry. Predicting the gas-phase deprotonation energy is relatively straightforward as I detail in Section 2.2 of my book. The difficulty is in treating the solvent and the interaction of the acid and its conjugate base in solution. Considering that we are most interested in acidities in water, a very polar solvent, the interactions between water and the conjugate base and the proton are likely to be large and important!

Baker and Pulay report a procedure for determining acidities with the aim of high throughput.¹ Thus, computational efficiency is a primary goal. Their approach is to compute the enthalpy change for deprotonation in solution using a continuum treatment and then employ a linear fit to predict the pK_a with the equation:

pK_a(c) = α_cΔH + β_c

where c designates a class of compound, such as alcohol, carboxylic acid, amine, etc. Fitting constants α_c and β_c need to be found then for each unique class of compound, where the fitting is to experimental pK_as in water. In their test suite, they employed eleven anilines and amines, seven pyridines, nine alcohols and phenols, and seven carboxylic acids.

They test a number of different computational variants: (a) what functional to employ, (b) what basis set to use for optimizing structures, and (c) what basis set to use for the enthalpy computation. They opt to employ COSMO for treating the solvent and quickly reject the use of gas phase structures (and particularly use of geometries obtained with molecular mechanics. Their ultimate model is OLYP/6-311+G**//3-21G(d) with the COSMO solvation model. Mean deviation is less than 0.4 pK units. They do note that use of HF or PW91 provides similar small errors, but ultimately favor OLYP for its computational performance.

While this procedure offers some guidance for future computation of acidity, I find a couple of issues. First, it relies on fitted parameters for every class of compound. If one is interested in a new class, then one must develop the appropriate parameters – and the experimental values may not be available or perhaps an insufficient number of them are experimentally available. Second, the parameters cover-up a great deal of problematic computational sins, like the solvation energy of the proton, small basis sets, missing correlation energies, missing dispersion corrections etc. A purist might hope for a computational algorithm that allows for systematic correction and improvement in the estimation of pK_as. Further work needs to be done to meet this higher goal.

References

(1) Zhang, S.; Baker, J.; Pulay, P., "A Reliable and Efficient First Principles-Based Method for Predicting pKa Values. 1. Methodology," J. Phys. Chem. A 2010, 114 , 425-431, DOI: 10.1021/jp9067069

Another benchmark study of the performance of different functionals – this time looking at the conformations of small alkanes.¹ Martin first establishes high level benchmarks: the difference between the trans and gauche conformers of butane: CCSD(T)/cc-pVQZ, 0.606 kcal mol^-1 and W1h-val, 0.611 kcal mol^-1; and the energy differences of the conformers of pentane, especially the TT and TG gap: 0.586 kcal mol^-1 at CCSD(T)/cc-pVTZ and 0.614 kcal mol^-1 at W1h-val.

They then examine the relative conformational energies of butane, pentane, hexane and a number of branched alkanes with a slew of functionals, covering the second through fifth rung of Perdew’s Jacob’s ladder. The paper has a whole lot of data – and the supporting
materials include Jmol-enhanced visualization of the structures! – but the bottom line is the following. The traditionally used functionals (B3LYP, PBE, etc) overestimate conformer energies while the MO6 family underestimates the interaction energies that occur in GG-type conformers. A dispersion correction tends to overcorrect and leads to wrong energy ordering of conformers. But the new double-hybrid functionals (B2GP-PLYP and B2K-PLYP) with the dispersion correction provide quite nice agreement with the CCSD(T) benchmarks.

Also worrisome is that all the functionals have issues in geometry prediction, particularly in the backbone dihedral angles. So, for example, B3LYP misses the τ₁ dihedral angle in the GG conformer by 5° and even MO6-2x misses the τ₂ angle in the TG conformer by 2.4&deg.

References

(1) Gruzman, D.; Karton, A.; Martin, J. M. L., "Performance of Ab Initio and Density Functional Methods for Conformational Equilibria of CnH2n+2 Alkane Isomers (n = 4-8),"
The Journal of Physical Chemistry A 2009, 113, 11974–11983 , DOI: http://dx.doi.org/10.1021/jp903640h

Here’s another extensive benchmarking study – this time on the use of TD-DFT to predict excitation energies.¹ This study looks at the performance of 28 different functionals, and compares the TD-DFT excitation energies against a data set of (a) computed vertical energies and (b) experimental energies. The performance is generally about the same for both data sets, with many functionals (especially the hybrid functionals) giving errors of about 0.3 eV. Performance can be a bit better when examining subclasses of compounds. For example, PBE0 and mPW1PW91 have a mean unsigned error of only 0.14 eV for a set of organic dyes.

References

(1) Jacquemin, D.; Wathelet, V.; Perpete, E. A.; Adamo, C., "Extensive TD-DFT Benchmark: Singlet-Excited States of Organic Molecules," J. Chem. Theory Comput., 2009, 5, 2420-2435, DOI: 10.1021/ct900298e