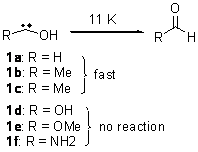
As we have noted in many previous posts, Schreiner has observed tunneling in hydroxycarbenes that is either very rapid (1a-c) or not at all (1d-f).^1-4 In a recent paper his group investigates whether cyclopropylhydroxycarbene 2 might have an intermediate lifetime due to the π-donating effect of the three-member ring.⁵

Schreiner makes this carbene in his usual manner: flash pyrolysis of the cyclopropylglyoxylic acid. Let’s now consider three possible rearrangements of carbene 2. The hydrogen can migrate (Scheme 1, path a) to give cyclopropylcarboxyaldehyde 3 similar to what was observed with the related hydroxycarbenes. Carbon can migrate (Scheme 1, path b), opening up the three-member ring to give the cyclobutenol 4. This ring could open to the diene 5 and tautomerize to the ketone 6. Lastly, a hydrogen migration from carbon (Scheme 1, path c) would lead to 7. The relative energies of these species computed at CCSD(T)//cc-pVTZ//M06-2x//6-311++G(d,p) are shown in Scheme 1.

Scheme 1. Relative energies in kcal mol^-1.

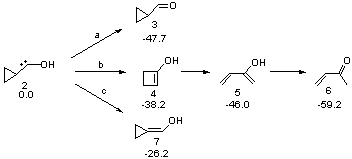
The computed barriers for the initial step of each pathway is +30.4 kcal mol^-1 for path a, +21.9 kcal mol^-1 for path b and +35.8 kcal mol^-1 for path c. Thus, one might expect to see only the reaction along path b at low temperature and mostly along b at high temperature with some small percent along path a. So what actually occurs?

After capturing the flash pyrolysis product in an Ar matrix, besides the unreacted cyclopropylglyoxylic acid, 6, 3, and 2 are observed in an approximate 8:5:1 ratio. 2 is identified on the basis of the nice agreement between the experimental and computed IR frequencies. Irradiation of 2 in the matrix leads to clean conversion to 4, also identified by comparison of the observed and computed IR frequencies. This is all consistent with the computed activation barriers. In the pyrolysis, at high T, 6 is the major product and 3 is the minor product. At very low T (11 K), irradiation of 2 produces 4 (crossing only the lowest barrier) and not continuing further along the rearrangement path to 6.

What is perhaps most exciting is that 2 disappears slowly in the dark at both 11 K and 20 K, converting at the same rate to 3. The half life is 17.7 h, much longer than for the alkyl and aryl substituted hydroxycarbenes 1a-c. This confirms the stabilization effect of the cyclopropyl group, as does its large singlet-triplet gap. The computed tunneling half-life using the WKB approach is 16.6 h, in excellent agreement with experiment. And as expected for a tunneling phenomenon, the dueterated analog has a much longer half-life, computed to be 10⁵ years. Experimentally, 2-d persists with no conversion to 3-d observed.

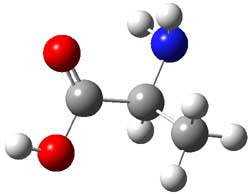
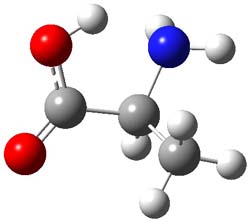
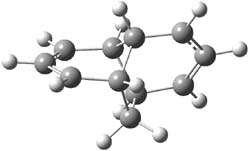
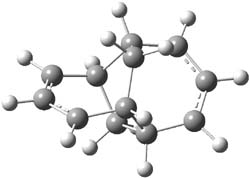
As with methylhydroxycarbene, we see here an example of tunneling control vs kinetic control. At high T, the reaction crosses the lowest barrier (shown in Figure 1a), proceeding to 4 and subsequent rearrangement products. At low T, the reaction crosses a higher barrier (shown in Figure 1b), but this path involves tunneling of the very light hydrogen atom only, producing 3.

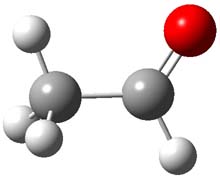
TS 2 → 3

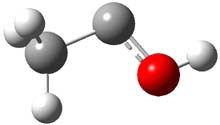
TS 2 → 4

Figure 1. M06-2X/6-311++G(d,p) optimized geometry of the transition states connecting 2 to (a) 3 and (b) 4.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard Iv, F. C.; Simmonett, A. C.; Allen, W. D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

(2) Schreiner, P. R.; Reisenauer, H. P., "Spectroscopic Identification of Dihydroxycarbene," Angew. Chem. Int. Ed., 2008, 47, 7071-7074, DOI: 10.1002/anie.200802105

(3) Gerbig, D.; Reisenauer, H. P.; Wu, C.-H.; Ley, D.; Allen, W. D.; Schreiner, P. R., "Phenylhydroxycarbene," J. Am. Chem. Soc., 2010, 132, 7273-7275, DOI: 10.1021/ja9107885

(4) Schreiner, P. R.; Reisenauer, H. P.; Ley, D.; Gerbig, D.; Wu, C.-H.; Allen, W. D., "Methylhydroxycarbene: Tunneling Control of a Chemical Reaction," Science, 2011, 332, 1300-1303, DOI: 10.1126/science.1203761.

(5) Ley, D.; Gerbig, D.; Wagner, J. P.; Reisenauer, H. P.; Schreiner, P. R., "Cyclopropylhydroxycarbene," J. Am. Chem. Soc., 2011, 133, 13614-13621, DOI: 10.1021/ja204507j

What is required in order to compute very accurate NMR chemical shifts? Harding, Gauss and Schleyer take on the interesting spectrum of 1-adamantyl cation to try to discern the important factors in computing its ¹³C and ¹H chemical shifts.¹

1

To start, the chemical shifts of 1-adamtyl cation were computed at B3LYP/def2-QZVPP and
MP2/qz2p//MP2/cc-pVTZ. The root means square error (compared to experiment) for the carbon chemical shifts is large: 12.76 for B3LYP and 6.69 for MP2. The proton shifts are predicted much more accurately with an RMS error of 0.27 and 0.19 ppm, respectively.

The authors speculate that the underlying cause of the poor prediction is the geometry of the molecule. The structure of 1 was optimized at HF/cc-pVTZ, MP2/cc-pVTZ and CCSD(T)/pVTZ and then the chemical shifts were computed using MP2/tzp with each optimized geometry. The RMS error of the ¹²C chemical shifts are HF/cc-pVTZ: 9.55, MP2/cc-pVTZ: 5.62, and CCSD(T)/pVTZ: 5.06. Similar relationship is seen in the proton chemical shifts. Thus, a better geometry does seem to matter. The CCSD(T)/pVTZ optimized structure of 1 is shown in Figure 1.

1

Figure 1. CCSD(T)/pVTZ optimized structure of 1.

Unfortunately, the computed chemical shifts at CCSD(T)/qz2p//CCSD(T)/cc-pVTZ are still in error; the RMS is 4.78ppm for the carbon shifts and 0.26ppm for the proton shifts. Including a correction for the zero-point vibrational effects and adjusting to a temperature of 193 K to match the experiment does reduce the error; now the RMS for the carbon shifts is 3.85 ppm, with the maximum error of 6 ppm for C3. The RMS for the proton chemical shifts is 0.21ppm.

The remaining error they attribute to basis set incompleteness in the NMR computation, a low level treatment of the zero-point vibrational effects (which were computed at HF/tz2p), neglect of the solvent, and use of a reference in the experiment that was not dissolved in the same media as the adamantyl cation.

So, to answer our opening question – it appears that a very good geometry and treatment of vibrational effects is critical to accurate NMR shift computation of this intriguing molecule. Let the
computational chemist beware!

References

(1) Harding, M. E.; Gauss, J.; Schleyer, P. v. R., "Why Benchmark-Quality Computations Are Needed To Reproduce 1-Adamantyl Cation NMR Chemical Shifts Accurately," J. Phys. Chem. A, 2011, 115, 2340-2344, DOI: 10.1021/jp1103356

InChI

1: InChI=1/C10H15/c1-7-2-9-4-8(1)5-10(3-7)6-9/h7-9H,1-6H2/q+1
InChIKey=HNHINQSSKCACRU-UHFFFAOYAC

Another remarkable piece of science from the Schreiner and Allen groups has appeared demonstrating the critical importance of combining experiment with computations.¹ (This one will surely be in the running for computational chemistry paper of the year.) Once again they examine tunneling from a carbene intermediate, but this time with an amazing conclusion that will have impact on chemistry textbooks!

Schreiner and Allen have previously examined a number of hydroxycarbenes (see these posts: A, B, C) and have found tunneling to be the main exit channel from these carbenes. The tunneling passes through barriers that are as large as 30 kcal mol^-1, and as expected, the deuterium labeled analogues have tunneling half lives that are exceptionally long, like 4000 years.

Now they examine methylhydroxycarbene 1,¹ which is interesting because there are two possible exit channels, leading to acetaldehyde 2 or vinyl alcohol 3. Previous gas-phase pyrolysis of pyruvic acid suggested the intermediacy of 1, which rearranges to 2 much more rapidly than to 3. However, G1 computations predict the barrier to 3 is smaller than the barrier to 2,² which should mean that 2 is the kinetic product!

Methylhydroxycarbene 1 was prepared by flash pyrolysis of pyruvic acid with capture of the products in an argon matrix. The carbene 1 was characterized by IR. The predicted frequencies (CCSD(T)/cc-pCVTZ – with corrections for anharmonicity) of 9 of the 11 bands of 1 are within 8 cm^-1 of the experimental frequencies. The OH and OD stretches, the ones not in agreement, are likely to be perturbed by the matrix. The predicted (MRCC/aug-cc-pVTZ) and experimental UV spectrum are also in close agreement.

Holding the matrix at 11 K and following the spectra of 1-3 led to the following important kinetic results: the half-life for formation of 2 is 66 min with no 3 observed to form. In addition, the rate for the deuterium labeled carbene to form 2 was too long for measuring, but was 196 minutes in Kr and 251 minutes in Xe. CCSD(T)/cc-pCVCZ computations followed by focal point methods gives the barrier to form acetaldehyde from 1 as 28.0 kcal mol^-1 while that to form vinyl alcohol 3 is much lower: 22.6 kcal mol^-1. (The structures of these three molecules and the transition states connecting them are shown in Figure 1.) Apparently, the reaction passes through or over the higher barrier in large preference over passing through or over the lower barrier!

1
TS12	2
TS13	3

Figure 1. CCSD(T)/cc-pCVTZ optimizes structures of 1-3 and the transition states connecting 1 to 2 and 1 to 3.

Precise mapping of the intrinsic reaction path at CCSD(T)/cc-pCVTZ allows for computing the WKB tunneling probabilities. This leads to the prediction of the half-life for the reaction 1 → 2 as 71 minutes, in excellent agreement with experiment. The computed half-life for the deuterium labeled reaction of 400 years and the computed half-life for 1 → 3 of 190 days are both in fine agreement with experiment.

Why does the reaction preferentially tunnel through the higher barrier? Well, the tunneling rate is dependent on the square root of the barrier height and linearly on the barrier width. The width is much smaller for the rearrangement to 2. The hydrogen needs to move a shorter amount in proceeding from 1to 2 than to 3, and in the rearrangement to vinyl alcohol a second hydrogen must migrate downwards to form the planar vinyl group. Basically, width beats out the height.

The important conclusion from this paper is the following: in addition to reactions being under kinetic or thermodynamic control, we must now consider a third options – a reaction under tunneling control!

A nice perspective on this paper and its implications has been written by Carpenter, who points out how this adds to our general notion of significant limitations to transition state theory.³

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Ley, D.; Gerbig, D.; Wu, C.-H.; Allen, W. D., "Methylhydroxycarbene: Tunneling Control of a Chemical Reaction," Science, 2011, 332, 1300-1303, DOI: 10.1126/science.1203761.

(2) Smith, B. J.; Nguyen Minh, T.; Bouma, W. J.; Radom, L., "Unimolecular rearrangements connecting hydroxyethylidene (CH₃-C-OH), acetaldehyde (CH₃-CH:O), and vinyl alcohol (CH₂:CH-OH)," J. Am. Chem. Soc., 1991, 113, 6452-6458, DOI: 10.1021/ja00017a015

(3) Carpenter, B. K., “Taking the High Road and Getting There Before You,” Science, 2011, 332, 1269-1270, DOI: 10.1126/science.1206693.

InChIs

1: InChI=1/C2H4O/c1-2-3/h3H,1H3
InChIKey=JVKQHDUTAFISFX-UHFFFAOYAN

2: InChI=1/C2H4O/c1-2-3/h2H,1H3
InChIKey=IKHGUXGNUITLKF-UHFFFAOYAB

3: InChI=1/C2H4O/c1-2-3/h2-3H,1H2
InChIKey=IMROMDMJAWUWLK-UHFFFAOYAT

The most favorable conformation of a carboxylic acid is the Z form. In fact, the E form is rarely found. Schreiner now offers an explanation for why this is so.¹

Photolysis of matrix-deposited benzoic acid revealed only the Z form (1Z). However, photolysis of deuterated benzoic acid did reveal the E form 1E, however it disappeared with a half-life of 12 minutes on argon at 11 K and 20 K. The lack of temperature dependence, and the huge isotope effect suggested that the isomerization proceeds via tunneling.

The tunneling rate was computed by generating the reaction path at CCSD(T)/cc-pVTZ with
MP2/cc-pVDZ zero point energy. This gave a half-life of 2.8 h for the deuterium species and 10^-5 min for the proton species. A Hammet-like relationship could be produced for the half-lives of para-substituted benzoic acids. Interestingly, a nice correlation is found between the computed width of the tunneling barrier and the half life with σ-donating ability.

References

(1) Amiri, S.; Reisenauer, H. P.; Schreiner, P. R., "Electronic Effects on Atom Tunneling: Conformational Isomerization of Monomeric Para-Substituted Benzoic Acid Derivatives," J. Am. Chem. Soc., 2010, 132 , 15902–15904, DOI: 10.1021/ja107531y

InChIs

Benzoic acid: InChI=1/C7H6O2/c8-7(9)6-4-2-1-3-5-6/h1-5H,(H,8,9)/f/h8H
InChIKey=WPYMKLBDIGXBTP-FZOZFQFYCI

How is the aromaticity of benzene affected by nitrogen substitution? Are pyridine and pyrimidine more or less aromatic than benzene? This question has been addressed many times, and Schleyer adds to this discussion with a B3LYP/6-311+G** study of the entire series of azines.¹ Analysis of the aromaticity is based on a two metrics: NICS(0)_πzz and extra cyclic resonance energy (ECRE). The NICS(0) _πzz value is now the ring current measurement advocated by Schleyer as it only includes the π orbitals and uses the tensor component perpendicular to the ring. ECRE is obtained by comparing block-localized energies of the azine to appropriate acyclic references.

Interestingly, both metrics give the same result, namely, that the aromaticity of benzene and all of the azines 1-6 are essentially equally aromatic.

References

(1) Wang, Y.; Wu, J. I. C.; Li, Q.; Schleyer, P. v. R., "Aromaticity and Relative Stabilities of Azines," Org. Lett., 2010, 12, 4824-4827, DOI: 10.1021/ol102012d

InChIs

1: InChI=1/C5H5N/c1-2-4-6-5-3-1/h1-5H
InChIKey=JUJWROOIHBZHMG-UHFFFAOYAY

2a: InChI=1/C4H4N2/c1-2-4-6-5-3-1/h1-4H
InChIKey=PBMFSQRYOILNGV-UHFFFAOYAA

2b: InChI=1/C4H4N2/c1-2-5-4-6-3-1/h1-4H
InChIKey=CZPWVGJYEJSRLH-UHFFFAOYAT

2c: InChI=1/C4H4N2/c1-2-6-4-3-5-1/h1-4H
InChIKey=KYQCOXFCLRTKLS-UHFFFAOYAV

3a: InChI=1/C3H3N3/c1-2-4-6-5-3-1/h1-3H
InChIKey=JYEUMXHLPRZUAT-UHFFFAOYAF

3b: InChI=1/C3H3N3/c1-2-5-6-3-4-1/h1-3H
InChIKey=FYADHXFMURLYQI-UHFFFAOYAY

3c: InChI=1/C3H3N3/c1-4-2-6-3-5-1/h1-3H
InChIKey=JIHQDMXYYFUGFV-UHFFFAOYAG

4a: InChI=1/C2H2N4/c1-2-4-6-5-3-1/h1-2H
InChIKey=DPOPAJRDYZGTIR-UHFFFAOYAI

4b: InChI=1/C2H2N4/c1-3-2-5-6-4-1/h1-2H
InChIKey=ZFXBERJDEUDDMX-UHFFFAOYAH

4c: InChI=1/C2H2N4/c1-3-5-2-6-4-1/h1-2H
InChIKey=HTJMXYRLEDBSLT-UHFFFAOYAH

5: InChI=1/CHN5/c1-2-4-6-5-3-1/h1H
InChIKey=ALAGDBVXZZADSN-UHFFFAOYAQ

6: InChI=1/N6/c1-2-4-6-5-3-1
InChIKey=YRBKSJIXFZPPGF-UHFFFAOYAK

Small energy differences pose a serious challenge for computation. The focal point analysis of Allen and Schaefer is one approach towards solving this problem, with energies extrapolated to the complete basis set limit at the HF and MP2 levels, and then corrections added on for higher-order effects.

These authors have applied the method to the conformations of alanine (similar to their previous study on cysteine – see this post).¹ There are two low energy conformers 1 and 2. The CCSD(T)/cc-pVTZ structures are shown in Figure 1. The HF/CBS estimate places 2 below 1, but this is reveres at MP2. With the correction for CCSD and CCSD(T), and core electrons, the energy gap is only 0.45 kJ mol^-1, favoring 1. Zero-point vibrational energy favors 1 by 1.66 kJ mol^-1, for a prediction that 1 is 2.11 kJ mol^-1 lower in energy than 2. It is interesting that most of this energy difference arises from differences in their ZPVE.

1

2

Figure 1. CCSD(T)/cc-pVTZ optimized geometries of the two lowest energy conformations of alanine.

The article also discusses the structures of these to conformers, obtained through a combination of theoretical treatment and revisiting the limited experimental measurements.

References

(1) Jaeger, H. M.; Schaefer, H. F.; Demaison, J.; Csaszar, A. G.; Allen, W. D., "Lowest-Lying Conformers of Alanine: Pushing Theory to Ascertain Precise Energetics and Semiexperimental R_e Structures," J. Chem. Theory Comput., 2010, 6, 3066-3078, DOI: 10.1021/ct1000236

InChIs

Alanine: InChI=1/C3H7NO2/c1-2(4)3(5)6/h2H,4H2,1H3,(H,5,6)/t2-/m0/s1/f/h5H
InChIKey=QNAYBMKLOCPYGJ-SNQCPAJUDI

Interacting bis-allyl radicals are the topic of a computational study by Gleiter and Borden.¹ The new twist is to have the two allyl groups interact through a cyclobutyl, cyclopentyl or cyclohexyl ring, as in 1-3.

The degree of interaction of the radical electrons is evaluated with a number of metrics. First, the singlet-triplet energy gap is computed at CASSCF(6,6)/6-31G(d) and UB3LYP/6-31G(d). A larger gap is suggestive of strong interaction between the two allyl radicals. Next, the <S²> value of the UB3LYP wavefunction will be 0 for a pure singlet, which occurs when the radicals are strongly interacting. A value near 1 suggests an electron localized into each allyl fragment. Lastly, the natural orbital occupation numbers (NOON) of the two highest lying orbitals would be 2 and 0 for the pure interacting state and each would be 1 for the non-interacting state. The B3LYP/6-31G(d) optimized geometries of 1-3 are shown in Figure 1. The values of each metric are listed in Table 1.

1	2
3

Figure 1. B3LYP/6-31G(d) optimized geometries of 1-3.

Table 1. Metrics for evaluating the allyl interaction in 1-3.

The different metrics are all consistent. The allyl radicals are strongly interacting in 1, with a low lying singlet state. The interaction is significantly lessened in 2 and smaller still in 3. The authors argue these differences in terms of the molecular orbital interactions between the allyl fragments and the central ring fragment.

References

(1) Lovitt, C. F.; Dong, H.; Hrovat, D. A.; Gleiter, R.; Borden, W. T., "Through-Bond Interactions in the Diradical Intermediates Formed in the Rearrangements of Bicyclo[n.m.0]alkatetraenes," J. Am. Chem. Soc., 2010, 132, 14617-14624, DOI: ja106329t

InChIs

1: InChI=1/C10H10/c1-3-7-9-5-2-6-10(7)8(9)4-1/h1-10H
InChIKey=QQZALYREQJSRLB-UHFFFAOYAA

2: InChI=1/C11H12/c1-3-8-7-9-4-2-6-11(8)10(9)5-1/h1-6,8-11H,7H2
InChIKey=XHSRXRHTBHVJQX-UHFFFAOYAV

3: InChI=1/C12H14/c1-3-9-7-12-6-2-5-11(9)8-10(12)4-1/h1-6,9-12H,7-8H2
InChIKey=JFNCWTOWDGQJLS-UHFFFAOYAA

The much publicized failure of common DFT methods to accurately describe alkane isomer energy and bond separation reactions (which I have blogged about many times) has recently been attributed to long-range exchange¹ (see this post) or simply just DFT exchange² (see this post). Grimme now responds by emphatically claiming that it is a failure in accounting for medium-range electron correlation.³

First, Grimme notes that the bond separation energy for linear alkanes (as defined in
Reaction 1) is underestimated by HF, and slightly overestimated by MP2, but SCS-MP2 provides energy in nice agreement with CCSD(T)/CBS energies. Since MP2 adds in coulomb correlation to the HF energy (which treats exchange exactly within a one determinant wavefunction), the traditional wavefunction approach strongly suggests a correlation error.

CH₃(CH₂)_mCH₃ + mCH₄ → (m+1)CH₃CH₃        Reaction 1

Next, bond separation energies computed with PBE and BLYP (which lack exact exchange), PBE0 (which has 25% non-local exchange) and BHLYP (which has 50% non-local exchange) are all similar and systematically too small. So, exchange cannot be the culprit. It must be correlation.

He also makes two other interesting points. First, inclusion of a long-range correction – his recently proposed D3 method⁴ – significantly improves results, but the bond separation energies are still underestimated. It is only with the double-hybrid functional B2PLYP and B2GPPLYP that very good bond separation energies are obtained. And these methods do address the medium-range correlation issue. Lastly, Grimme notes that use of zero-point vibrational energy corrected values or enthalpies based on a single conformation are problematic, especially as the alkanes become large. Anharmonic corrections become critical as does inclusion of multiple conformations with increasing size of the molecules.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett., 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

(2) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys., 2009, DOI: 10.1039/b818412g.

(3) Grimme, S., "n-Alkane Isodesmic Reaction Energy Errors in Density Functional Theory Are Due to Electron Correlation Effects," Org. Lett. 2010, 12, 4670–4673, DOI: 10.1021/ol1016417

(4) Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H., "A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu," J. Chem. Phys., 2010, 132, 154104, DOI: 10.1063/1.3382344.

Borden predicted measurable heavy-atom isotope effects in the ring opening of cyclopropylcarbinyl radical. In my blog post on this paper, I concluded with the line:

Borden hopes that experimentalists will reinvestigate this
problem (and hopefully confirm his predictions).

Well, in a recent paper where Borden collaborates with Singleton, these predictions are confirmed!¹

There is a sizable kinetic isotope effect for breaking the ring bond to a ¹²C over a bond to a ¹³C atom, up to 16% at -100 °C. The KIE predicted without including tunneling are dramatically below the experimental values, but incorporation of tunneling in the computated KIEs match up with experiment with an error no greater that 0.7%. The Arrhenius plot of ln KIE vs. 1/T shows enhanced isotope effects when tunneling is included, very nice agreement between the experimental and tunneling-corrected KIEs and curvature – all indicative of heavy atom tunneling. Lastly, the ring open product (1-butene) is the observed major product (62%) at -100 °C; the minor product is methylcyclopropane. In the absence of heavy-atom tunneling, 1-butene would be the minor product (28%).

References

(1) Gonzalez-James, O. M.; Zhang, X.; Datta, A.; Hrovat, D. A.; Borden, W. T.; Singleton, D. A. J. Am. Chem. Soc., 2010, 132, 12548-12549, DOI: 10.1021/ja1055593.

InChIs

Cyclopropylcarbonyl radical: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2
InChIKey=RMCDUNHIVVEEDD-UHFFFAOYAR

1-butene: InChI=1/C4H8/c1-3-4-2/h3H,1,4H2,2H3
InChIKey=VXNZUUAINFGPBY-UHFFFAOYAZ

I have had a long-standing interest in organolithium compounds, dating back to my graduate student days. Thus, I was excited to read Kass and Radom’s latest work on the computational and experimental evaluation of the acidity of lithium acetylide LiCCH.¹

The gas phase experimental acidity is accomplished by preparing the conjugate base of lithium acetylide through a procedure of collision-induced dissociation with loss of CO₂, as in Scheme 1. By reacting this anion with a variety of different acids, they were able to bracket the acidity and determine that ΔH_acid is 391.0 ± 1.3 kcal mol^-1. This is about 13 kcal mol^-1 less acidic than acetylene itself. The reduction is acidity understandable in terms of the C-Li being essentially ionic, and thereby loss of the proton builds up negative charge on a carbon adjacent to a carbon that already has a great deal of negative charge.

Scheme 1

Computations support this enthalpy for deprotonation. The G3, G4 and W1 values for the enthalpy deprotonation of lithium acetylide are 389.1, 388.9, and 390.4 kcal mol^-1, respectively. It should also be noted that the conjugate base of lithium acetylide posses a non-classical bridging geometry 1, which is well-known for organolithium species.²

References

(1) Meyer, M. M.; Chan, B.; Radom, L.; Kass, S., R., "Gas-Phase Synthesis and Reactivity of Lithium Acetylide Ion, LiCC^–," Angew. Chem. Int. Ed., 2010, 49, 5161-5164, DOI: 10.1002/anie.201001485

(2) Streitwieser, A.; Bachrach, S. M.; Dorigo, A.; Schleyer, P. v. R. In Lithium Chemistry: A Theoretical and Experimental Overview; Sapse, A.-M., Schleyer, P. v. R., Eds.; Wiley-Interscience: New York, 1995, p 1-45.