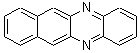
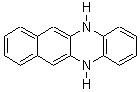
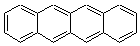
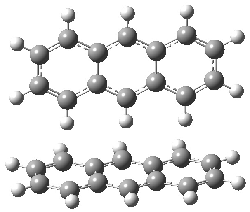
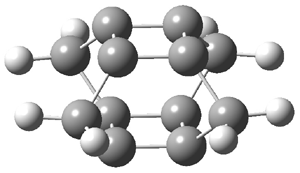
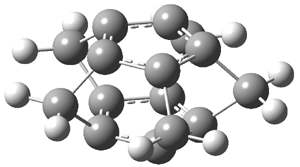
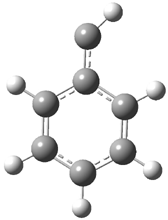
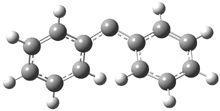
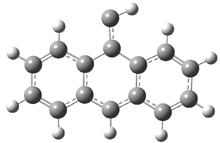
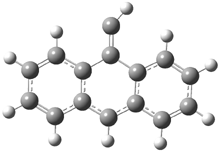
Schleyer continues his study of aromaticity with a paper¹ that picks up on the theme presented in one² I have previously blogged on – the relationship between a formally aromatic pyrazine and formally antiaromatic dihydropyrazine. He now examines the diazotetracene 1 and it dihydro analogue 2.¹ In terms of formal electron count, 1 should be aromatic, just like the all carbon analogue tetracene 3, and 2 should be antiaromatic.

Schleyer used the NICS_πzz values obtained in the center of each ring to evaluate the aromatic/antiaromatic character of these three molecules. These calculations were performed using canonical molecular orbitals and repeated using localized molecular orbitals. The results are similar for each method, and the canonical MO values are presented in Table 1. As expected for an aromatic compound, each ring of tetracene 3 has large negative NICS values, indicating that each ring is locally aromatic and the molecule as a whole is aromatic. The same is true for the diazotetracene 1. (In fact the NICS values for 1 and 3 are remarkably similar.) However, for 2, the dihydropyrazine ring has a positive NICS values, indicative of a locally antiaromatic ring. While the three phenyl rings have negative NICS values, these absolute values are smaller than for the rings of 1 or 3, indicating an attenuation of their aromaticity. Nonetheless, the sum of the NICS values of 2 is negative, suggesting that the molecule is globally aromatic, though only marginally so. This is due to the antiaromaticity of the dihydropyrazine ring being delocalized to some extent over the entire molecule. Schleyer, concludes that “large 4n π compounds […] are not appreciably destabilized relative to their 4n+2 π congeners.”

Table 1 NICS_πzz (ppm) for each ring of 1-3 and their sum.¹

References

(1) Miao, S.; Brombosz, S. M.; Schleyer, P. v. R.; Wu, J. I.; Barlow, S.; Marder, S. R.; Hardcastle, K. I.; Bunz, U. H. F., "Are N,N-Dihydrodiazatetracene Derivatives Antiaromatic?," J. Am. Chem. Soc., 2008, 130, 7339-7344, DOI: 10.1021/ja077614p.

(2) Miao, S.; Schleyer, P. v. R.; Wu, J. I.; Hardcastle, K. I.; Bunz, U. H. F., "A Thiadiazole-Fused N,N-Dihydroquinoxaline: Antiaromatic but Isolable," Org. Lett. 2007, 9, 1073-1076, DOI: 10.1021/ol070013i

InChIs

1: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

2: InChI=1/C16H10N2/c1-2-6-12-10-16-15(9-11(12)5-1)17-13-7-3-4-8-14(13)18-16/h1-10H

3: InChI=1/C16H12N2/c1-2-6-12-10-16-15(9-11(12)5-1)17-13-7-3-4-8-14(13)18-16/h1-10,17-18H

Wes Borden has been exploring reactions where tunneling is operational. These studies have been inspired by Bill Doering’s¹ statement regarding tunneling in 1,5-sigmatropic shifts: “The tunneling effect is likely, in the opinion of some, to remain relegated to the virtual world of calculations”. Borden’s first two papers dealt with the kinetic isotope effects for the [1,5]-H shift in 1,3-cyclopentadiene and 5-methyl-1,3-cyclopentadiene.^2,3

His latest article examines carbon tunneling,⁴ which, due to the much heavier mass of the carbon nucleus relative to a proton, is likely to play a minimal role at best. Borden looked at the ring opening of cyclopropylcarbinyl radical 1 to 3-butene-1-yl radical 2, passing through transition state TS1-2. The B3LYP/6-31G(d) optimized structures are shown in Figure 1.

1		2
1	TS1-2	2

Figure 1. B3LYP/6-31G(d) optimized geometries of 1, 2, and TS1-2.⁴

The predicted rate of the reaction at 298 K using canonical variational transition state theory is increased by about 50% when small-curvature tunneling is included. This predicted rate is a bit smaller than the experimental value. Experiments also shows a linear Arrhenius plot, and Borden’s calculations agree until one reaches very low temperatures. Below 150 K the Arrhenius curve begins to deviate from linearity, and below 20 K the curve is flat – the rate is no longer temperature dependent! Thus, at cryogenic temperatures, the tunneling rate far exceeds traditional crossing of the variational barrier. Borden hopes that experimentalists will reinvestigate this problem (and hopefully confirm his predictions).

References

(1) Doering, W. v. E.; Zhao, X., "Effect on Kinetics by Deuterium in the 1,5-Hydrogen Shift of a Cisoid-Locked 1,3(Z)-Pentadiene, 2-Methyl-10-methylenebicycloJ. Am. Chem. Soc., 2006, 128, 9080-9085, DOI: 10.1021/ja057377v.

(2) Shelton, G. R.; Hrovat, D. A.; Borden, W. T., "Tunneling in the 1,5-Hydrogen Shift Reactions of 1,3-Cyclopentadiene and 5-Methyl-1,3-Cyclopentadiene," J. Am. Chem. Soc., 2007, 129, 164-168, DOI: 10.1021/ja0664279.

(3) Shelton, G. R.; Hrovat, D. A.; Borden, W. T., "Calculations of the Effect of Tunneling on the Swain-Schaad Exponents (SSEs) for the 1,5-Hydrogen Shift in 5-Methyl-1,3-cyclopentadiene. Can SSEs Be Used to Diagnose the Occurrence of Tunneling?," J. Am. Chem. Soc., 2007, 129, 16115-16118, DOI: 10.1021/ja076132a.

(4) Datta, A.; Hrovat, D. A.; Borden, W. T., "Calculations Predict Rapid Tunneling by Carbon from the Vibrational Ground State in the Ring Opening of Cyclopropylcarbinyl Radical at Cryogenic Temperatures," J. Am. Chem. Soc., 2008, 130, 6684-6685, DOI: 10.1021/ja801089p.

InChIs

1: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2

2: InChI=1/C4H7/c1-3-4-2/h3H,1-2,4H2

The importance of the interactions between neighboring aromatic molecules cannot be overemphasized – π-π-stacking is invoked to explain the structure of DNA, the hydrophobic effect, molecular recognition, etc. Nonetheless, the nature of this interaction is not clear. In fact the commonly held notion of π-π orbital overlap is not seen in computations.

Grimme¹ has now carefully examined the nature of aromatic stacking by comparison with aliphatic analogues. He has examined dimers formed of benzene 1, naphthalene 2, anthracene 3, and teracene 4 and compared these with the dimers of their saturated analogues (cyclohexane 1s, decalin 2s, tetradecahydroanthracene 3s, and octadecahydrotetracene 4s. The aromatic dimmers were optimized in the T-shaped and stacked arrangements, and these are shown for 3 along with the dimer of 3s in Figure 1. These structures are optimized at B97-D/TZV(2d,2p) – a functional designed for van der Waals compounds. Energies were then computed at B2LYP-D/QZV3P, double-hybrid functional that works very well for large systems.

Figure 1. Optimized structures of 3s, 3t, and 3a.

The energies for formation of the complexes are listed in Table 1. The first interesting result here is that the benzene and naphthalene dimmers (whether stacked or T-shaped) are bound by about the same amount as their saturated analogues. Grimme thus warns that “caution is required to not overestimate the effect of the π system”.

Table 1. Complexation energy (kcal mol^-1)

The two larger aromatics here do show a significantly enhanced complexation energy than their saturated analogues, and Grimme refers to this extra stabilization as the π-π stacking effect (PSE). Energy decomposition analysis suggests that electrostatic interactions actually favor the complexation of the saturated analogues over the aromatics. However, Pauli exchange repulsion essentially cancels the electrostatic attraction for all the systems, and it is dispersion that accounts for the dimerization energy. Dispersion increases with size of the molecule, and “classical” dispersion forces (the R^-6 relationship) accounts for more than half of the dispersion energy in the saturated dimmers, while it is the non-classical, or orbital-based, dispersion that dominates in the stacked aromatic dimmers. Grimme attributes this to “special nonlocal electron correlations between the π electrons in the two fragments at small interplane distances”.

References

(1) Grimme, S., "Do Special Noncovalent π-π Stacking Interactions Really Exist?," Angew. Chem. Int. Ed., 2008, 47, 3430-3434, DOI: 10.1002/anie.200705157.

InChIs

1: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H

1s: InChI=1/C6H12/c1-2-4-6-5-3-1/h1-6H2

2: InChI=1/C10H8/c1-2-6-10-8-4-3-7-9(10)5-1/h1-8H

2s: InChI=1/C10H18/c1-2-6-10-8-4-3-7-9(10)5-1/h9-10H,1-8H2

3: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H

3s: InChI=1/C14H24/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h11-14H,1-10H2

4: InChI=1/C18H12/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h1-12H

4s: InChI=1/C18H30/c1-2-6-14-10-18-12-16-8-4-3-7-15(16)11-17(18)9-13(14)5-1/h13-18H,1-12H2

Duncan and Schleyer¹ have investigated protonated acetylene and the protonated acetylene dimer. These ions are created in a pulsed supersonic nozzle/pulsed electrical discharge with a weakly bound argon atom as a tag. IR laser photodissociation spectroscopy allows for the detection of peaks down to 2000 cm^-1, a region not previously explored for this cation. The experimental IR spectrum for H⁺(C₂H₂)^.Ar has two main features: at 3146 and 2217 cm^-1. The 3146 cm^-1 corresponds to the previously observed peak² at 3142 cm^-1 and is similar to the absorption in acetylene (3136 cm^-1). MP2/6-311+G(2d,2p) computations were performed on the classical and non-classical structures of H⁺(C₂H₂), with and without a complexed argon atom. These geometries are displayed in Figure 1 and the predicted vibrational frequencies are listed in Table 1.

Figure 1. MP2/6-311+

Table 1. Relative energies (kcal mol^-1) and frequencies of protonated acetylene
and the protonated acetylene-argon cluster.¹

The argon tag only slightly perturbs the spectrum, as expected for a weakly bond atom remote from most of the hydrogen atoms. The predicted spectra of the two non-classical ions are in nice agreement with the experiment – particularly the interesting peak at 2123 cm^-1 that is due to the bridged proton. This spectra, and the confirmation of the bridging, non-classical structure, makes a nice pair with the recently reported bridging, non-classical structure of the ethyl cation,³ which I blogged on previously.

The spectrum of the H⁺(C₄H₄) ion show a doublet at 3129 and 3158 cm^-1 and two small peaks at 1261 and 1365 cm^-1. The computed structure that comes closest to matching this spectrum is for the asymmetrically bridged dimer (See Figure 2), though is much more energetic than its isomers. The authors speculate that the bridged dimer is trapped in an energy-well during the thermal expansion, which prevents the formation of the lower energy isomers.

Figure 2. Schematic drawing and relative energies of the H⁺(C₄H₄) ion.
(Note – unfortunately the authors have supplied insufficient information in the Supporting Materials to completely define the geometries of these molecules!)

References

(1) Douberly, G. E.; Ricks, A. M.; Ticknor, B. W.; McKee, W.
C.; Schleyer, P. v. R.; Duncan, M. A., "Infrared Photodissociation
Spectroscopy of Protonated Acetylene and Its Clusters," J. Phys. Chem. A, 2008, 112, 1897-1906, DOI: 10.1021/jp710808e.

(2) Gabrys, C. M.; Uy, D.; Jagod, M. F.; Oka, T.; Amano, T., "Infrared Spectroscopy of Carboions. 8. Hollow Cathode Spectroscopy of Protonated Acetylene, C2H3+," J. Phys. Chem., 1995, 99, 15611-15623, DOI: 10.1021/j100042a042.

(3) Andrei, H.-S.; Solcà, N.; Dopfer, O., "IR Spectrum of the Ethyl Cation: Evidence
for the Nonclassical Structure," Angew. Chem. Int. Ed., 2008, 47, 395-397, DOI: 10.1002/anie.200704163

A real tour-de-force experimental and computational study of the ORD of 2,3-hexadiene 1 has been produced through the combined efforts of Wiberg, Jorgensen, Crawford, Cheeseman and colleagues.¹ You might not expect a simple compound like 1 to display anything particularly unusual, but you’d be wrong!

2,3-hexadiene exists as three conformations, shown in Figure 1. The cis conformers is the lowest energy form, but the other two are only 0.2 kcal mol^-1 higher in energy, meaning that all three will have significant mol fractions at 0 °C, as listed in Figure 1. The optical rotation for each conformer was determined using B3LYP/aug-cc-pVDZ and CCSD/aug-ccpVDZ. While there is some disagreement in the values determined by the two methods, what is most interesting is that large dependence of [α]_D on the conformation – see Table 1!

cis 0.0 (0.441)

gauche120 0.269 (0.280)

gauche240 0.272 (0.279)

Figure 1. CCSDT optimized geometries of 1, their relative energies (kcal mol^-1) and, in parenthesis, their mol fractions at 0 °C.¹

Table 1. Calculated [α]_D for 1.

^aUsing the aug-ccpVDZ basis set. ^aBoltzman averaged based on the populations shown in Figure 1.

The ORD spectrum of 1 was taken for neat liquid and in the gas phase. The computed and experimental optical rotations are listed in Table 2. Two interesting points can be made from this data. First, the optical activity of 1 is strongly affected by phase. Second, the computed optical rotations, especially the CCSD values, are in fairly good agreement with the gas-phase experimental values.

Table 2. Boltzmann-weighted computed and experimental optical rotations of 1.

A hypothesis to account for the large difference in the gas- and liquid-phase ORD for 1 is that the conformational distribution changes with the phase. The gas and liquid-phase ORD of 2,3-pentadiene shows the same strong phase dependence, even though this compound exists as only one conformer.

Next, a Monte Carlo simulation of gas- and liquid-phase 1 was performed to assess the conformational distributions. Though the range of dihedral angle distributions span about 60°, the population distribution is nearly identical in the two phases – there is no medium-dependence on the conformation distribution, and so this cannot explain the difference in the gas and liquid ORDs.

The authors also tested for the vibrational dependence on the optical rotation. While there is a small correction due to vibrations, it is not enough to account for the differences due to the medium. The origin of this effect remains unexplained.

References

(1) Wiberg, K. B.; Wang, Y. g.; Wilson, S. M.; Vaccaro, P. H.; Jorgensen, W. L.; Crawford, T. D.; Abrams, M. L.; Cheeseman, J. R.; Luderer, M., "Optical Rotatory Dispersion of 2,3-Hexadiene and 2,3-Pentadiene," J. Phys. Chem. A, 2008, DOI: 10.1021/jp076572o.

InChIs

1: InChI=1/C6H10/c1-3-5-6-4-2/h3,6H,4H2,1-2H3/t5-/m1/s1 InChIKey=DPUXQWOMYBMHRN-RXMQYKEDBA

What happens when antiaromatic rings stack? One can draw an MO interaction diagram for π-stacked cyclobutadiene dimer (Figure 1) and recognize at once that this cluster should be stabilized. In fact, it is reminiscent of an orbital diagram for an aromatic species!

Figure 1. MO Interaction diagram of stacked butadiene (modified from Ref 1).

Houk had examined just this dimer (1) in 1996 and located a D_4h critical point at CASSCF(8,8)/6-31G* (see Figure 2).² This structure is energetically below two isolated cyclobutadiene molecules; however, it is a second-order saddle point.

1

Figure 1. CASSCF(8,8)/6-31G* optimized structure of 1.

Schleyer has examined a series of superphanes constructed from anti- and aromatic rings linked by methano bridges, 2-7.¹ These structures were optimized at B3LYP/6-311+G** and their magnetic properties computed at GIAO-PW91. The optimized structures of 3 and 4 are shown in Figure 3.

3

4

Figure 3. B3LYP/6-311+G** optimized structures of 3 and 4.¹

The inter-ring separation (D) in these compounds is quite interesting (Table 1). It decreases in the series 2-4, with the distance in the latter compound of only 2.002 Å. The inter-ring distance is much larger in 5, which has two (aromatic) benzene rings. All of the other comounds (except 2) have shorter distances and these all involve antiaromatic rings. These short distances for the antiaromatic superphanes suggests stabilizing interactions between the rings, as indicated by the MO diagram of Figure 1.

Table 1. Inter-ring distance and NICS values for 2-7.¹

^aDistance (Å) between the carbon of one ring and the closest carbon of the second ring.

The NICS values are also interesting. Schleyer computed a variety of different NICS values, and we list here the isotropic NICS value at the cage center (NICS_cage) and the zz-component evaluated 1 Å above the ring on the outside face NICS(1)_zzring). The NICS(1)_zzring is perhaps the best measure of magnetic properties related to aromatic/antiaromatic character. All six compounds have rings that have negative values of NICS(1)_zzring, indicating of aromatic character. In fact, the value for 5 is less negative than for isolated benzene alone. This suggests that the stacked antiaromatic rings become aromatic, while the stacked aromatic rings become less aromatic. For all six compounds, the NICS_cage value is negative indicating diatropicity, associated with aromatic character – again consistent with the MO argument presented in Figure 1. To answer our lead off question, stacked antiaromatic rings are aromatic!

References

(1) Corminboeuf, C.; Schleyer, P. v. R.; Warner, P., "Are Antiaromatic Rings Stacked Face-to-Face Aromatic?," Org. Lett. 2007, 9, 3263-3266, DOI: 10.1021/ol071183y.

(2) Li, Y.; Houk, K. N., "The Dimerization of Cyclobutadiene. An ab Initio CASSCF Theoretical Study," J. Am. Chem. Soc. 1996, 118, 880-885, DOI: 10.1021/ja921663m.

InChIs

2: InChI=1/C9H6/c1-4-6-2-7-5(1)9(7)3-8(4)6/h1-3H2/q-2

3: InChI=1/C12H8/c1-5-7-2-8-6(1)10-3-9(5)11(7)4-12(8)10/h1-4H2

4: InChI=1/C15H10/c1-6-8-2-9-7(1)11-3-10(6)14-5-15(11)13(9)4-12(8)14/h1-5H2/q+2

5: InChI=1/C18H12/c1-7-9-2-10-8(1)12-3-11(7)15-5-16(12)18-6-17(15)13(9)4-14(10)18/h1-6H2

6: InChI=1/C21H14/c1-8-10-2-11-9(1)13-3-12(8)16-5-17(13)21-7-20(16)18-6-19(21)15(11)4-14(10)18/h1-7H2/q-2

7: InChI=1/C24H16/c1-9-11-2-12-10(1)14-3-13(9)17-5-18(14)22-7-21(17)23-8-24(22)20-6-19(23)15(11)4-16(12)20/h1-8H2

In the book I extensively discuss the singlet-triplet gap of methylene and some of the chemistry of phenylcarbene. Schleyer and Schaefer have now reported computations on the singlet-triplet gap of arylcarbenes.¹ The geometries of phenylcarbene 1, diphenylcarbene 2, 1-naphthylcarbene 3, bis(1-naphtyl)carbene 4, and 9-anthrylcarbene 5 were optimized at B3LYP/6-311+G(d,p). These geometries are shown in Figure 1.

1s	1t
2s	2t
3s	3t
4s	4s
4s	4s

Figure 1. B3LYP/6-311+G(d,p) optimized structures of singlet and triplet 1-5.

Since this functional is known to underestimate the singlet-triplet gap of carbenes, they employ an empirical correction based on the difference in this gap for methylene between the computed value (11.89 kcal mol^-1) and the experimental value (9.05 kcal mol^-1). These corrected energy gaps are listed in Table 1.

Table 1. Corrected singlet-triplet energy gaps (kcal mol^-1) at B3LYP/6-311+G(d,p).

Using the following isodesmic reactions, they estimate the stabilization of the singlet or triplet carbene afforded by the aryl substituent:

R-C-H + CH₄ → H-C-H + R-CH₃

R-C-R + CH₄ → R-C-H + R-CH₃

These isodesmic energies are listed in Table 2. For phenylcarbne, the phenyl group stabilizes the singlet more than the triple, reducing the ST gap by 6.3 kcal mol^-1. However, adding a second phenyl group (making 2) stabilizes both the singlet and triplet by about the same amount, leading to little change in the ST gap. The singlet does not get accrue the potential benefit of the second aryl group because sterics prohibit the two rings from being coplanar.

Table 2. Aryl effect for 1-5 based on the isodesmic reaction energies (kcal mol^-1)

References

(1) Woodcock, H. L.; Moran, D.; Brooks, B. R.; Schleyer, P. v. R.; Schaefer, H. F., "Carbene Stabilization by Aryl Substituents. Is Bigger Better?," J. Am. Chem. Soc., 2007, 129, 3763-3770, DOI: 10.1021/ja068899t.

InChIs

1: InChI=1/C7H6/c1-7-5-3-2-4-6-7/h1-6H

2: InChI=1/C13H10/c1-3-7-12(8-4-1)11-13-9-5-2-6-10-13/h1-10H

3: InChI=1/C11H8/c1-9-5-4-7-10-6-2-3-8-11(9)10/h1-8H

4: InChI=1/C21H14/c1-2-8-19-14-16(12-13-17(19)6-1)15-20-10-5-9-18-7-3-4-11-21(18)20/h1-14H

5: InChI=1/C15H10/c1-11-14-8-4-2-6-12(14)10-13-7-3-5-9-15(11)13/h1-10H

Robinson and Schleyer report the synthesis of and computations on the novel structure gallepin 1.¹ This is the gallium analogue of tropyllium, the prototype of a seven-member aromatic ring. Robinson actually prepared the bis-benzannulated analogue 2, which is found to coordinate to TMEDA in the crystal.

Schleyer computed (B3LYP/LANL2DZ) the gallepin portion of 2 in its naked form 3 and associated with trimethylamine 4. The crystal structure of 2 reveals that the 7 member ring is boat-shaped, and this is reproduced in the computed structure of 4. Interestingly, the naked gallepin is planar, suggestive of an aromatic structure. NICS_πZZ computations were performed to gauge the aromaticity of these compounds. The value for the 7-member ring is -9.0 in 4 and -9.9 in 3, indicating aromatic character. These values are less then in the parent gallepin 1, which has a value of -15.3, but this is the normal type of diminishment expected from benzannulation.
But borapin has a NICS_πZZ substantially more negative (-27.7) and so gallepins are less aromatic than borapins. Nonetheless, it is very interesting that aromaticity can be extended in this interesting way – different heteroatom and different ring size.

3	4

References

(1) Quillian, B.; Wang, Y.; Wei, P.; Wannere, C. S.; Schleyer, P. v. R.; Robinson, G. H., "Gallepins. Neutral Gallium Analogues of the Tropylium Ion: Synthesis, Structure, and Aromaticity," J. Am. Chem. Soc., 2007, 129, 13380-13381, DOI: 10.1021/ja075428d.

Truhlar and Cramer have updated their Solvation Model to SM8.¹ This model allows for any solvent to be utilized (both water and organic solvents) and treats both neutral and charged solutes. While there are some small theoretical changes to the model, the major change is in how the parameters are selected, the number of parameters, and a much more extensive data set is used for the fitting procedure.

Of note is how well this new model works. Table 1 compares the errors in solvation free energies computed using the new SM8 model against some other popular continuum methods. Clearly, SM8 provides much better results. As they point out, what is truly discouraging is the performance of the 3PM model against the continuum methods. 3PM stands for “three-parameter model”, where the solvation energies of all the neutral solute in water is set to their average experimental value (-2.99 kcal mol^-1), and the same for the neutral solutes in organic solvents (-5.38 kcal mol^-1), and for ions (-65.0 kcal mol^-1). The 3PM outperforms most of the continuum methods!

Table 1. Mean unsigned error (kcal mol^-1) for the solvation
free energies computed with different methods.¹

^a274 data points. ^b666 data points spread among 16 solvents. ^c332 data points spread among acetonitrile, water, DMSO, and methanol. ^dUsing mPW1PW/6-31G(d). ^eUsing mPW1PW/6-31G(d) and the UA0 atomic radii in Gaussian. ^fUsing mPW1PW/6-31G(d) and the UAHF atomic radii in Gaussian. ^gUsing B3LYP/6-31G(d) and conductor-PCM in GAMESS. ^hUsing B3LYP/6-31G(d) and the PB method in Jaguar.

References

(1) Marenich, A. V.; Olson, R. M.; Kelly, C. P.; Cramer, C. J.; Truhlar, D. G., "Self-Consistent Reaction Field Model for Aqueous and Nonaqueous Solutions Based on Accurate Polarized Partial Charges," J. Chem. Theory Comput., 2007, 3, 2011-2033. DOI: 10.1021/ct7001418.

Peter Vollhardt and Ken Houk have teamed up on an interesting account of pericyclic reactions of molecules related to starphenylene.¹ This touches on the nature of aromatic compounds and pericyclic reaction mechanisms, topics I take up in a few places in the book.

Compound 1 rearranges at 120 °C to 3, and the presumed pathway is
through 2 – the simultaneous [2+2+2] ring opening through the all-disrotatory path.
However, the computed (B3LYP/6-31G(d) activation energy is 34.6 kcal mol^-1 for this path, much higher than the experimental activation enthalpy, which is 28.9 kcal mol^-1.

The alternative path is to sequential break the cyclobutene rings with the standard conrotatory stereochemistry. This would give 4 and the barrier is 32.5 kcal mol^-1, in better agreement with experiment. From here, there is a bond shift, which traverses a Möbius geometry – as proposed by Karney and Castro (see the book and also this previous post). An electrocylization, followed by a Diels-Alder cycloaddition completes the path to 3. The rate determining step is the first: 1 ↔ 4.

On the other hand, upon heating 5 produces 6. Here the computed barrier for the [2+2+2] reaction (32.6 kcal mol^-1) is in nice agreement with the experimental value (34.1 kcal mol^-1), while the stepwise pathway has a much higher barrier (39.9 kcal mol^-1). They did not locate the polycyclic analogue of 3 (namely, 7) in the reaction of 5. This may be due in part to the fact that the bond shift is accompanied by a loss of aromaticity.

References

(1) Eichberg, M. J. H., K. N.; Lehmann, J.; Leonard, P. W.; Märker, A.; Norton, J. E.; Sawicka, D.; Vollhardt, K. P. C. W., G. D.; Wolff, S., "The Thermal Retro[2+2+2] cycloaddition of Cyclohexane Activated by Triscyclobutenannelation: Concerted All-Disrotatory versus Stepwise Conrotatory Pathways to Fused [12]Annulenes," Angew. Chem. Int. Ed., 2007, 46, 6894-6898, DOI: 10.1002/anie.200702474

InChIs

1: InChI=1/C24H30/c1-2-8-14-13(7-1)19-20(14)22-17-11-5-6-12-18(17)24(22)23-16-10-4-3-9-15(16)21(19)23/h19-24H,1-12H2/t19-,20+,21-,22+,23-,24+

2: InChI=1/C24H30/c1-2-8-20-15-16-22-10-5-6-12-24(22)18-17-23-11-4-3-9-21(23)14-13-19(20)7-1/h13-18H,1-12H2/b14-13-,16-15-,18-17-,19-13-,20-15+,21-14+,22-16+,23-17+,24-18-

3: InChI=1/C24H30/c1-2-8-14-13(7-1)19-21-15-9-3-4-10-16(15)22-20(14)23(19)17-11-5-6-12-18(17)24(21)22/h19-24H,1-12H2

4: InChI=1/C24H30/c1-2-8-20-15-16-22-10-5-6-12-24(22)18-17-23-11-4-3-9-21(23)14-13-19(20)7-1/h13-18H,1-12H2/b14-13+,16-15+,18-17+,19-13-,20-15+,21-14+,22-16-,23-17-,24-18+

5: InChI=1/C24H18/c1-2-8-14-13(7-1)19-20(14)22-17-11-5-6-12-18(17)24(22)23-16-10-4-3-9-15(16)21(19)23/h1-12,19-24H/t19-,20+,21-,22+,23-,24+

6: InChI=1/C24H18/c1-2-8-20-15-16-22-10-5-6-12-24(22)18-17-23-11-4-3-9-21(23)14-13-19(20)7-1/h1-18H/b14-13-,16-15-,18-17-,19-13-,20-15+,21-14+,22-16+,23-17+,24-18-

7: InChI=1/C24H18/c1-2-8-14-13(7-1)19-21-15-9-3-4-10-16(15)22-20(14)23(19)17-11-5-6-12-18(17)24(21)22/h1-12,19-24H