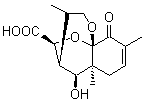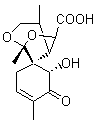Cramer and Hoye have applied DFT computations to the predictions of both protons and carbon NMR chemical shifts in penam β-lactams¹ using the procedure previously described in my blog post Predicting NMR chemical shifts. They examined the compounds 1-8 by optimizing low energy conformers at B3LYP/6-31G(d) with IEFPCM (solvent=chloroform). The chemical shifts were then computed using these geometries with the larger 6-311+G(2d,p) basis set and four different functionals: B3LYP, PBE1 and the two specific functionals designed to produce proton and carbon chemical shifts: WP04 and WC04.

A number of interesting results are reported. First, all three functionals do a fine job in predicting the proton chemical shifts of 1-8, with WP04 slightly better than the other two.On the other hand, all three methods fail to predict the carbon chemical shifts of 1-3, though B3LYP and PBE1 do correctly identify 5-8. The failure of WC04 is surprising, especially since dimethyl disulfide was used in the training set. They also noted that WP04 using just the minimum energy conformation (as opposed to a Boltzmann averaged chemical shift sampled from many low energy conformers) did correctly identify lactams 1-4. This is helped by the fact that the lowest energy conformer constituted anywhere form 37% to 68% of the energy-weighted population.

References

(1) Wiitala, K. W.; Cramer, C. J.; Hoye, T. R., “Comparison of various density functional methods for distinguishing stereoisomers based on computed ¹H or ¹³C NMR chemical shifts using diastereomeric penam ?-lactams as a test set,” Mag. Reson. Chem., 2007, 45, 819-829, DOI: 10.1002/mrc.2045.

InChIs

1: InChI=1/C18H17NO5S/c1-18(2)14(17(23)24-3)19-15(22)11(16(19)25-18)10-12(20)8-6-4-5-7-9(8)13(10)21/h4-7,10-11,14,16H,1-3H3/t11-,14+,16+/m0/s1

5: InChI=1/C17H15NO5S/c1-17(2)13(16(22)23)18-14(21)10(15(18)24-17)9-11(19)7-5-3-4-6-8(7)12(9)20/h3-6,9-10,13,15H,1-2H3,(H,22,23)/t10-,13+,15+/m0/s1

Schleyer and Houk¹ offer a provocative paper examining the reference compounds that one chooses when trying to evaluate such concepts as ring strain energy and aromaticity. I discuss this at length in Chapter 2 of the book, focusing on the isodesmic, homodesmotic, and group equivalent reactions.

Their work starts with the isodesmic reaction

CH₃CH₂CH₃ + CH₄ → 2 CH₃CH₃

and note that this reaction is endothermic by 2.83 kcal mol^-1. They argue that 1,3-dialkyl interactions are stabilizing, and call this effect “protobranching”.

Gronert^2,3 has recently described the counterargument – that 1,3-dialkyl groups are repulsive – but whether the interaction is attractive or repulsive is not my concern here. Let’s proceed assuming that protobranching is in fact stabilizing.

Schleyer and Houk demonstrate that the stabilization of protobranching is nicely additive. In Table 1 are simple bond separation (isodesmic) reactions of straight-chain alkanes and cycloalkanes. This can then be extended to argue for why branched alkanes are more stable than their straight-chain analogues – namely, branched chains have more 1,3-dialkyl interactions and these are stabilizing. They note that the group separation reaction of iso-butane is more endothermic than that of pentane, yet the difference is neatly ascribed to protobranching.

Table 1. Energy of reactions and energy per protobranch (PB) using experimental heats of formation.

Now the interesting aspect is when this concept of protobranching is applied to ring systems. The conventional (homodesmotic) reaction for cyclopropane is

(CH₂)₃ + 3 C₂H₆ → 3 CH₃CH₂CH₃ ΔH = -27.7 kcal mol^-1

Schleyer and Houk argue that protobranching is not balanced in this reaction, and the consequence is that since propane is stabilized by about 2.8 kcal mol^-1, the reaction energy should be reduced by 8.4 kcal mol^-1. Thus the ring strain energy (RSE) of cyclopropane is 19.3 kcal mol^-1. This is essentially the value obtained when one employs the isodesmic reaction to evaluate the RSE of cyclopropane, namely

(CH₂)₃ + 3 CH₄ → 3 C₂H₆ ΔH = -19.2 kcal mol^-1

And this isodesmic reaction has balanced protobrancing (none!) on both sides. The reaction that balances protobranching (two on each side) for obtaining the RSE of cyclobutane is

(CH₂)₄ + 2 CH₄ → 2 CH₃CH₂CH₃ ΔH = -21.0 kcal mol^-1

Protobranching corrections need also be made to the question of aromatic stabilization energy or resonance energy of benzene. For example, since cyclohexane is invoked as one of the reference compounds in the following reaction, the resulting energy must be corrected for six protobranching interactions.

2 C₂H₄ + (CH₂)6 → (CH)₆ + 3 C₂H₆

The question now becomes “Is protobranching real and do we need to correct for it?” Further studies should be performed.

References

(1) Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K. N.; Schleyer, P. v. R., "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations," Chem. Eur. J. 2007, 13, 7731-7744, DOI: 10.1002/chem.200700602

(2) Gronert, S., "Evidence that Alkyl Substitution Provides Little Stabilization to Radicals: The C-C Bond Test and the Nonbonded Interaction Contradiction," J. Org. Chem., 2006, 71, 7045-7048, DOI: 10.1021/jo060797y.

(3) Gronert, S., "An Alternative Interpretation of the C-H Bond Strengths of Alkanes," J. Org. Chem., 2006, 71, 1209-1219, DOI: 10.1021/jo052363t.

I mentioned “mindless chemistry” in the interview with Fritz Schaefer. This term, the title of the article by Schaefer and Schleyer,¹ refers to locating minimum energy structures through a stochastic search driven solely by a computer algorithm. No chemical rationale or intuition is used; rather, the computer simply tries a slew of different possibilities and mindlessly marches through them.

The approach employed by Schaefer and Schleyer is to use the ‘kick” algorithm of Saunders.² An arbitrary initial geometry is first selected (Saunders even suggests the case where all atoms are located at the same point!) and then a kick is applied to each atom, with random direction and displacement, to create a new geometry. An optimization is then performed with some quantum mechanical method, to produce a new structure. The kick is then applied to this new structure (or to the initial one again) to generate another geometry to start up another optimization. By doing many different “kicks” with different kick size, one can span a large swath of configuration space.

In their first “mindless chemistry” paper, Schafer and Schleyer identified some new structures of BCONS, C₆Be and C₆Be^2-.¹ In their next application,³ they explored the novel molecule periodane, which has the molecular formula LiBeBCNOF, named to reflect its make-up of one atom of every element (save neon) on the first full row of the periodic table. Krüger⁴ located the planar structure 1 (see Figure 1). But Schaefer and Schleyer, employing the “kick” algorithm located 27 structures that are lower in energy than 1, Their lowest energy structure 2 is 122 kcal mol^-1 lower than 1. They advocate for this stochastic search to gain broad understanding of the nature of the potential energy surface and then refining the search using “human logic”.

1

2

Figure 1. Optimized structures of periodane 1 and 2.

(Note – I have only provided a sketch of 2 since the supporting information for the article has not yet been posted on the Wiley web site. I will update this post with the actual structure when it becomes available.)

References

(1) Bera, P. P.; Sattelmeyer, K. W.; Saunders, M.; Schaefer, H. F.; Schleyer, P. v. R., "Mindless Chemistry," J. Phys. Chem. A, 2006, 110, 4287-4290, DOI: 10.1021/jp057107z.

(2) Saunders, M., "Stochastic Search for Isomers on a Quantum Mechanical Surface," J. Comput. Chem.. 2004, 25, 621-626, DOI: 10.1002/jcc.10407

(3) Bera, P. P.; Schleyer, P. v. R.; Schaefer, H. F., III, "Periodane: A Wealth of Structural Possibilities Revealed by the Kick Procedure," Int. J. Quantum Chem. 2007, 107, 2220-2223, DOI: 10.1002/qua.21322

(4) Krüger, T., "Periodane – An Unexpectedly Stable Molecule of Unique Composition," Int. J. Quantum Chem. 2006, 106, 1865-1869, DOI: 10.1002/qua.20948

Jorgensen reports an enhanced QM/MM and ab initio study of the rate enhancement of Diels-Alder reactions in various solvents.¹ This study extends earlier studies that he and others have done, many of which are discussed in Chapter 6.2 of the book. In this study, he reports QM/MM computations using the PDDG/PM3 method for the QM component, and MP2 computations incorporating CPCM to account for bulk solvent effects.

The major advance in methodology in this paper is performing a two-dimensional potential of mean force analysis where these two dimensions correspond to the forming C-C distances. In addition, computations were done for water, methanol, acetonitrile and hexane as solvents. Highlights of the results are listed in Table 1.

Table 1. Computed bond asynchronicity^a and activation energy^b (kcal/mol) for the Diels-Alder reaction with cyclopentadiene.

The semi-empirical method underestimates the asynchronicity of these gas-phase Diels-Alder TSs. However, with inclusion of the solvent, the computations do indicate a growing asynchronicity with solvent polarity, This is associated with the ability of the solvent, especially protic solvents, to preferentially hydrogen bond to the carbonyl in the TS.

In terms of energetics, in must first be pointed out that the computations dramatically overestimate the activation barriers. However, the relative trends are reproduced: the barrier increases from water to methanol to acetonitrile to hexane. Jorgensen also computed the activation barriers at MP2/6-311+G(2d,p) with CPCM using the CBS=QB3 gas phase geometries. Some of these results are listed in Table 2. The results for water are in outstanding agreement with experiment. However, the results for the other solvents are poor, underestimating the increase in barrier in moving to the more polar solvent.

Table 2. MP2/6-311+G(2d,p)/CPCM values for ΔG^‡ (kcal/mol).

Bottom line, the conclusions of this study are in agreement with the earlier studies, namely that the hydrophobic effect (better may be the enforced hydrophobic interaction) and greater hydrogen bonding in the TS (both more and stronger hydrogen bonds) account for the rate acceleration of the Diels-Alder reaction in water.

References

(1) Acevedo, O.; Jorgensen, W. L., "Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theory Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.

Kass has once again uncovered a simple system that challenges our notions of basic chemical concepts. It is a well accepted notion that the most acidic proton of all of the amino acids is the carboxylic acid one. However, acidities are strongly influenced by the solvent, and the absence of solvent in the gas phase can dramatically alter things.

Kass and co-workers examined the gas-phase acidity of cysteine with computational and
experimental techniques.¹ The lowest energy conformer of cysteine is 1a, characterized by having three intramolecular hydrogen bonds (Figure 1). The next lowest conformer, 1b, has only two intramolecular hydrogen bonds and is 1.5 kcal mol^-1 higher in energy at G3B3.

1a xyz	1b xyz

Figure 1. B3LYP/aug-cc-pVDZ optimized structures of cysteine 1.¹

They optimized a number of different configurations of the conjugate base of cysteine: two conformers from the loss of the carboxylate proton (2a and 2b), two conformers from the loss of the thiol proton (2c and 2d), and one conformer from the loss of the thiol proton of the zwitterion (2e). These structures are shown in Figure 2 along with their relative energies. All of these structures possess two intramolecular hydrogen bonds.

2a (3.1) xyz	2b (3.4) xyz
2c (0.0) xyz	2d (5.1) xyz
2e (10.1) xyz

Figure 2. B3LYP/aug-cc-pVDZ optimized structures of the conjugate base of cysteine 2. Relative energies (kcal mol^-1) in parenthesis computed at G3B3.¹

The gas phase acidity of carboxylic acids is greater than thiols; the deprotonation energy of propanoic acid (CH₃CH₂CO₂H) is 347.7 kcal mol^-1 at G3B3 (347.2 expt.²), about 6 kcal mol^-1 less than that of ethanethiol (CH₂CH₂SH: 355.0 at G3B3 and 354.2 expt.²). However, the computations indicate that 2c is the lowest energy structure of deprotonated cysteine, and 2c comes about by loss of the thiol proton! Te lowest energy cysteine conjugate base from loss of the carboxylate proton is 1a, which is 3.1 kcal mol^-1 higher in energy. Apparently, the hydrogen bonding network in 2c is quite favorable, able to make up for the inherent favorability of a carboxylate over a thiolate anion.

The G3B3 computed deprotonation energy of cysteine is 333.3 kcal mol^-1 (for removal of the thiol proton). Kass determined the deprotonation energy of cysteine using a kinetic and a thermodynamic method. The kinetic method gives a value of 332.9 ± 3.3 kcal mol^-1­, while the thermodynamic method gives 334.4 ± 3.3 kcal mol^-1­. These are in fine agreement with the computed value.

This study ably demonstrates the dramatic role that solvent can play in determining molecular properties. Kass titled the article “Are carboxyl groups the most acidic sites in amino acids?” and answers with “no” – in the gas phase the thiol group is more acidic. He ends the article with an indication that the alcohol of tyrosine may be competitive in acidity with its carboxylic group, too.

References

(1) Tian, Z.; Pawlow, A.; Poutsma, J. C.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidity, H/D Exchange Experiments, and Computations on Cysteine and Its Conjugate Base," J. Am. Chem. Soc., 2007, 129, 5403-5407, DOI: 10.1021/ja0666194.

(2) NIST, NIST Chemistry WebBook, 2005, http://webbook.nist.gov/.

InChIs

1: InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)

I just ran across a nice summary article by Peter Schreiner¹ detailing the recent spate of articles describing problems with many DFT methods, especially the ubiquitous B3LYP functional. This article covers essentially the same ground as my previous post Problems with DFT.

References

(1) Schreiner, P. R., “Relative Energy Computations with Approximate Density Functional Theory – A Caveat!,” Angew. Chem. Int. Ed., 2007, 46, 4217-4219, DOI: 10.1002/anie.200700386.

Another three applications of computed NMR chemical shifts towards structure identification have appeared, dealing with carbohydrates and natural products.

Prediction of NMR Signals of Carbohydrates

The study by Cramer and Hoye¹ investigates identification of diastereomers with NMR, in particular, identification of cis and trans isomers of 2-methyl- (1), 3-methyl- (2), and 4-methylcyclohexanol (3). The study discusses the ability of different DFT methods to predict the chemical shifts of these alcohols in regard to distinguishing their different configurations. An interesting twist is that they have developed a functional specifically suited to predict proton chemical shifts and a second functional specifically for predicting carbon chemical shifts.²

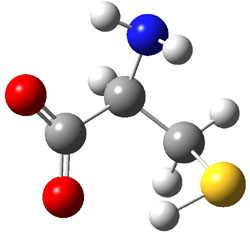
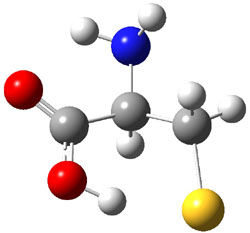
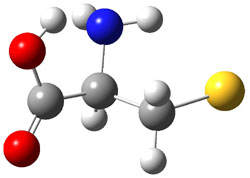
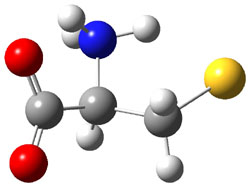
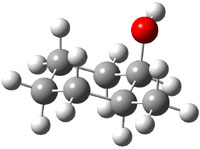
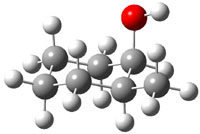
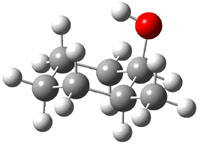
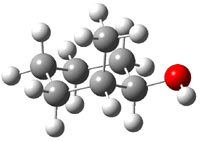
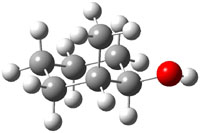
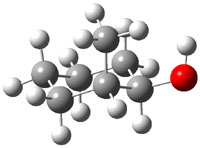
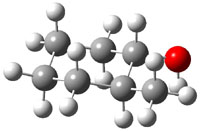
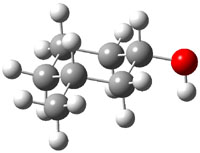
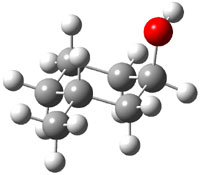
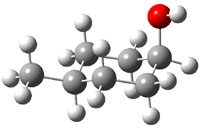
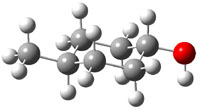
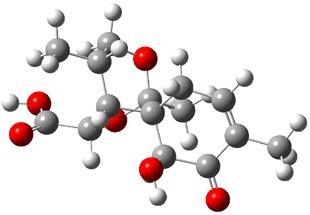
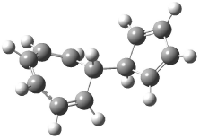
The approach they take was first to optimize the six different conformations for each diastereomer including solvent (chloroform). They chose to optimize the structures at B3LYP/6-311+G(2d,p) with PCM. The six conformers (notice the axial/equatorial relationships, along with the position of the alcohol hydrogen) of 1c are presented in Figure 1. Chemical shifts were then obtained with a number of different methods, weighting them according to a Boltzmann distribution.

0.0 xyz	0.20 xyz	0.73 xyz
1.23 xyz	1.56 xyz	1.85 xyz

Figure 1. PCM/B3LYP/6-311+G(2d,p) optimized structures of the conformers of 1c. Relative energies (kcal mol^-1) are listed for each isomer.

Now a brief digression into how they developed their modified functional.² They define the exchange-correlation functional (see Chapter 1.3.1 of my book – or many other computational chemistry books!) as

      E_xc = P₂E_x(HF) + P₃ΔE_x(B) + P₄E_x(LSDA) + P₅ΔE_c(LYP) + P₆E_c(LSDA)

where the Ps are parameters to be fit and E_x(HF) is the Hartree-Fock exchange energy, ΔE_x(B) is the Becke gradient correction to the local spin-density approximation (LSDA), E_x(LSDA) is the exchange energy, ΔE_c(LYP) is the Lee-Yang-Parr correction to the LSDA correlation energy, and E_c(LSDA) is the LSDA correlation energy. Chemical shifts were computed for proton and carbon, and the parameters P were adjusted (between 0 and 1) to minimize the error in the predicted chemical shifts from the experimental values. A total of 43 different molecules were used for this fitting procedure. The values of the parameters are given for the carbon functional (WC04), the proton functional (WP04) and B3LYP (as a reference) in Table 1. Note that there is substantial difference in the values of the parameter among these three different functionals.

Table 1. Values of the parameters P for the functionals WC04, WP04, and B3LYP.

Now, the computed proton and carbon chemical shifts using 4 different functions (B3LYP, PBE1, MP04, and WC04) for 1-3 were compared with the experiment values. This comparison was made in a number of different ways, but perhaps most compellingly by looking at the correlation coefficient of the computed shifts compared with the experimental shifts. This was done for each diastereomer, i.e. the computed shifts for 2c and 2t were compared with the experimental shifts of both 2c and 2t. If the functional works well, the correlation between the computed and experimental chemical shifts of 2c (and 2t) should be near unity, while the correlation between the computed shifts of 2c and the experimental shifts of 2t should be dramatically smaller than one. This is in fact the case for all three functionals. The results are shown in Table 2 for B3LYP and WP04, with the later performing slightly better. The results for the carbon shifts are less satisfactory; the correlation coefficients are roughly the same for all comparisons with B3LYP and PBE1, and WC04 is only slightly improved.
Nonetheless, the study clearly demonstrates the ability of DFT-computed proton chemical shifts to discriminate between diasteromers.

Table 2. Correlation coefficients between the computed and experimental proton chemical shifts.^a

	2ccomp (1.06) xyz	2tcomp (0.0) xyz
2cexp   2texp	0.9971 0.9985 0.8167 0.8098	0.8334 0.9050 0.9957 0.9843
	3c (0.0) xyz	3t (0.63) xyz
3cexp   3texp	0.9950 0.9899 0.8856 0.9310	0.8763 0.8717 0.9990 0.9979
	4c (0.54) xyz	4t (0.0) xyz
4cexp   4texp	0.9993 0.9975 0.8744 0.8675	0.8335 0.9279 0.9983 0.9938

^aPCM/B3LYP/6-311+G(2d,p)//PCM/ B3LYP/6-31G(d) in regular type and PCM/WP04/6-311+G(2d,p)//PCM/ B3LYP/6-31G(d) in italic type. Relative energy (kcal mol^-1) of the most favorable conformer of each diastereomer is given in parenthesis.

Predicting NMR of Natural Products

Bagno has a long-standing interest in ab initio prediction of NMR. In a recent article, his group takes on the prediction of a number of complex natural products.³ As a benchmark, they first calculated the NMR spectra of strychnine (4) and compare it with its experimental spectrum. The optimized PBE1PBE/6-31G(d,p) geometry of 4 is drawn in Figure 2. The correlation between the computed NMR chemical shifts for both ¹H and ¹³C is quite good, as seen in Table 3. The corrected mean average errors are all very small, but Bagno does point out that four pairs of proton chemical shifts and three pairs of carbon chemical shifts are misordered.

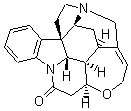
Strychnine 4

Figure 2. PBE1PBE/6-31G(d,p) geometry of strychnine 4.³

Table 3. Correlation coefficient and corrected mean average error
(CMAE) between the computed and experiment chemical shifts of 4.

The study of the sesquiterpene carianlactone (5) demonstrates the importance of including solvent in the NMR computation. The optimized B3LYP/6-31G(d,p) geometry of 5 is shown in Figure 3, and the results of the comparison of the computed and experimental chemical are listed in Table 4. The correlation coefficient is unacceptable when the x-ray structure is used. The agreement improves when the gas phase optimized geometry is employed, but the coefficient is still too far from unity. However, optimization using PCM (with the solvent as pyridine to match experiments) and then computing the NMR chemical shifts in this reaction field provides quite acceptable agreement between the computed and experimental chemical shifts.

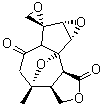
Corianlactone 5

Figure 3. B3LYP/6-31G(d,p) geometry of carianlactone 5.³

Table 4. Correlation coefficient and corrected mean average error (CMAE) between
the computed and experiment chemical shifts of 5.

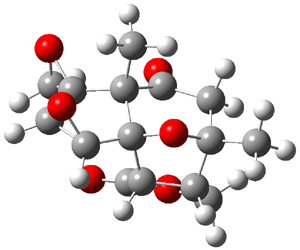
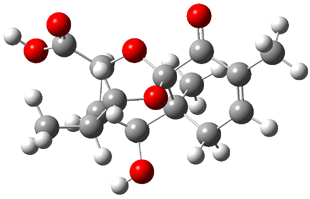
Lastly, Bagno took on the challenging structure of the natural product first identified as boletunone B (6a).⁴ Shortly thereafter, Steglich reinterpreted the spectrum and gave the compound the name isocyclocalopin A (6b).⁵ A key component of the revised structure was based on the δ 0.97 ppm signal that they assigned to a methyl above the enone group, noting that no methyl in 6a should have such a high field shift.

Bagno optimized the structures of 6a and 6b at B3LYP/6-31G(d,p), shown in Figure 4. The NMR spectra for 6a and 6b were computed with PCM (modeling DMSO as the solvent). The correlation coefficients and CMAE are much better for the 6b model than for the 6a model., supporting the reassigned structure. However, the computed chemical shift for the protons of the key methyl group in question are nearly identical in the two proposed structures: 1.08 ppm in 6a and 1.02 ppm in 6b. Nonetheless, the computed chemical shifts and coupling constants of 6b are a better fit with the experiment than those of 6a.

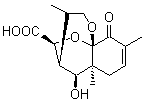
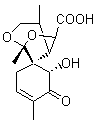
boletunone B 6a	isocyclocalopin A 6b

Figure 4. B3LYP/6-31G(d,p) geometry of the proposed structures of Boletunone B, 6a and 6b.³

Table 5. Correlation coefficient and corrected mean average error (CMAE) between the computed (B3LYP/6-31G(d,p) + PCM) and experiment chemical shifts of 6a and 6b.

In a similar vein, Nicolaou and Frederick has examined the somewhat controversial structure of maitotxin.⁶ For the sake of brevity, I will not draw out the structure of maitotxin; the interested reader should check out its entry in wikipedia. The structure of maitotoxin has been extensively studied, but in 2006, Gallimore and Spencer⁷ questioned the stereochemistry of the J/K ring juncture. A fragment of maitotoxin that has the previously proposed stetreochemistry is 7. Gallimore and Spencer argued for a reversed stereochemistry at this juncture (8), one that would be more consistent with the biochemical synthesis of the maitotoxin. Nicolaou noted that reversing this stereochemistry would lead to other stereochemical changes in order for the structure to be consistent with the NMR spectrum. Their alternative is given as 9.

7

8

9

Nicolaou and Freferick computed ¹³C NMR of the three proposed fragments 7-9 at B3LYP/6-31G*; unfortunately they do not provide the coordinates. They benchmark this method against brevetoxin B, where the average error is 1.24 ppm, but they provide no error analysis – particularly no regression so that corrected chemical shift data might be employed. The best agreement between the computed and experimental chemical shifts is for 7, with average difference of 2.01 ppm. The differences are 2.85 ppm for 8 and 2.42 ppm for 9. These computations support the original structure of maitotoxin. The Curious Wavefunction blog discusses this topic, with an emphasis on the possible biochemical implication.

References

(1) Wiitala, K. W.; Al-Rashid, Z. F.; Dvornikovs, V.; Hoye, T. R.; Cramer, C. J., "Evaluation of Various DFT Protocols for Computing ¹H and ¹³C Chemical Shifts to Distinguish Stereoisomers: Diastereomeric 2-, 3-, and 4-Methylcyclohexanols as a Test Set," J. Phys. Org. Chem. 2007, 20, 345-354, DOI: 10.1002/poc.1151

(2) Wiitala, K. W.; Hoye, T. R.; Cramer, C. J., "Hybrid Density Functional Methods Empirically Optimized for the Computation of ¹³C and ¹H Chemical Shifts in Chloroform Solution," J. Chem. Theory Comput. 2006, 2, 1085-1092, DOI: 10.1021/ct6001016

(3) Bagno, A.; Rastrelli, F.; Saielli, G., "Toward the Complete Prediction of the ¹H and ¹³C NMR Spectra of Complex Organic Molecules by DFT Methods: Application to Natural Substances," Chem. Eur. J. 2006, 12, 5514-5525, DOI: 10.1002/chem.200501583

(4) Kim, W. G.; Kim, J. W.; Ryoo, I. J.; Kim, J. P.; Kim, Y. H.; Yoo, I. D., "Boletunones A and B, Highly Functionalized Novel Sesquiterpenes from Boletus calopus," Org. Lett. 2004, 6, 823-826, DOI: 10.1021/ol049953i

(5) Steglich, W.; Hellwig, V., "Revision of the Structures Assigned to the Fungal Metabolites Boletunones A and B," Org. Lett. 2004, 6, 3175-3177, DOI: 10.1021/ol048724t.

(6) Nicolaou, K. C.; Frederick, M. O., "On the Structure of Maitotoxin," Angew. Chem. Int. Ed., 2007, 46, 5278-5282, DOI: 10.1002/anie.200604656.

(7) Gallimore, A. R.; Spencer, J. B., "Stereochemical Uniformity in Marine Polyether Ladders – Implications for the Biosynthesis and Structure of Maitotoxin," Angew. Chem. Int. Ed. 2006, 45, 4406-4413, DOI: 10.1002/anie.200504284.

InChI

1: InChI=1/C7H14O/c1-6-4-2-3-5-7(6)8/h6-8H,2-5H2,1H3
2: InChI=1/C7H14O/c1-6-3-2-4-7(8)5-6/h6-8H,2-5H2,1H3
3: InChI=1/C7H14O/c1-6-2-4-7(8)5-3-6/h6-8H,2-5H2,1H3
4: InChI=1/C21H22N2O2/c24-18-10-16-19-13-9-17-21(6-7-22(17)11-12(13)5-8-25-16)14-3-1-2-4-15(14)23(18)20(19)21/h1-5,13,16-17,19-20H,6-11H
5: InChI=1/C14H14O6/c1-12-2-6(15)8-13(4-18-13)9-10(19-9)14(8,20-12)7-5(12)3-17-11(7)16/h5,7-10H,2-4H2,1H3/t5-,7-,8?,9+,10+,12+,13?,14-/m1/s1
6a: InChI=1/C15H20O6/c1-7-4-5-14(3)12(17)9-8(2)6-20-15(14,11(7)16)21-10(9)13(18)19/h4,8-10,12,17H,5-6H2,1-3H3,(H,18,19)/t8-,9+,10+,12+,14-,15-/m1/s1
6b: InChI=1/C15H20O6/c1-7-4-5-15(12(17)10(7)16)9-8(2)6-20-14(15,3)21-11(9)13(18)19/h4,8-9,11-12,17H,5-6H2,1-3H3,(H,18,19)/t8?,9-,11?,12+,14-,15-/m1/s1

The search for unusual potential energy surface topologies continues. Unusual surfaces can lead to dynamic effects that result in rates and product distributions dramatically divergent from that predicted by statistical theories. I addressed this topic in Chapter 7 of the book.

Houk has found another interesting example in the Diels-Alder reaction of cyclopentadiene with nitrostyrene 1.¹ The [4+2] adduct is 2, which can undergo a [3,3] Cope-like rearrangement to give 3. Product 3 can also result from a [2+4] Diels-Alder cycloaddition where cyclopentadiene acts as the dienophile.

Like some of the examples in Chapter 7, the potential energy surface, computed at B3LYP/6-31+G*, contains a single transition state (TS1) from reactants. Continuing on the reaction path past the transition state, a valley ridge inflection point (VRI) intervenes, causing the path to bifurcate: one path leads to 2 and the other leads to 3. In other words, a single transition state leads to two different products! TS1 is geometrically closer to 2 than 3, while TS2 lies closer to 3 than 2 (Figure 1). This topology directs most molecules to traverse a path over TS1 and on to 2. What is novel in this paper is that the acid-catalyzed reaction, using SnCl₄, shifts TS1 towards 3 and TS2 towards 2, leading to the opposite product distribution. The uncatalyzed reaction favors formation of 2 while the catalyzed reaction favors 3 over 2. Confirmation of this prediction awaits a molecular dynamics study.

TS1	TS1-Cat
TS2	TS2-Cat

Figure 1. B3LYP/6-31+G(d) optimized structures for TS1 and TS2.¹

References

(1) Celebi-Olcum, N.; Ess, D. H.; Aviyente, V.; Houk, K. N., “Lewis Acid Catalysis Alters the Shapes and Products of Bis-Pericyclic Diels-Alder Transition States,” J. Am. Chem. Soc., 2007, 129, 4528-4529. DOI: 10.1021/ja070686w

InChI

1: InChI=1/C8H7NO2/c10-9(11)7-6-8-4-2-1-3-5-8/h1-7H/b7-6+
2: InChI=1/C13H13NO2/c15-14(16)13-11-7-6-10(8-11)12(13)9-4-2-1-3-5-9/h1-7,10-13H,8H2
3: InChI=1/C13H13NO2/c15-14-9-12(10-5-2-1-3-6-10)11-7-4-8-13(11)16-14/h1-6,8-9,11-13H,7H2

In the pursuit of further elucidation of just what the concepts “aromatic” and “antiaromatic” mean, Schleyer and Bunz reported the preparation and characterization of a novel antiaromatic compound that is isolable.¹

Bunz synthesized the redox pair of compounds 1 and 2 that differ in the electron count in the pi-system. The former (1) has 14 π electrons and should be aromatic, while the latter (5) has 16 π electrons and should be antiaromatic. The NMR spectrum of both compounds was measured and compared to the computed signals of the parent compounds 3 and 4. The signals match very nicely. The structures of 1 and 2 were further confirmed by x-ray crystallography. 1 and 2 can be interconverted by redox reactions and 2 is stable in air, only slowly oxidizing to 1.

The NICS(0)_πizz values computed for 3 and 4 are shown in Figure 1. (See ref 2 for a discussion on this NICS method and also Chapter 2 of my book.) These values are quite negative for each ring of 3, consistent with its expected aromatic character. On the other hand, the NICS value for each ring of 4 is more positive than the corresponding ring of 3, with the value in the center of the pyrazine ring being positive. These NICS values indicate that 4 is certainly less aromatic than 3, and perhaps even expresses antiaromatic character.

Figure 1. NICS(0)_πzz values for 3 and 4 computed at PW91/6-311G**.

Interestingly, hydrogenation of 3 to give 4 is -14.0, indicating that while 3 appears to be a normal aromatic compound, 4, if it is antiaromatic, exhibits some energetic stabilization. They identify this stabilization as a result of the interaction between the dihydropyrazine ring and the thidiazole ring, evidenced in the exothermicity of the isodemic reaction:

So while 4 may be antiaromatic, it appears to be energetically reasonably stable. It is important to keep in mind though that 4 is not the most stable tricycle isomer; in fact, 5 is 7 kcal mol^-1 lower in energy than 4.

Schleyer and Bunz conclude that antiaromaticity may “not result in a prohibitive energetic penalty.”

References

(1) Miao, S.; Schleyer, P. v. R.; Wu, J. I.; Hardcastle, K. I.; Bunz, U. H. F., "A Thiadiazole-Fused N,N-Dihydroquinoxaline: Antiaromatic but Isolable," Org. Lett. 2007, 9, 1073-1076, DOI: 10.1021/ol070013i

(2) Fallah-Bagher-Shaidaei, H.; Wannere, C. S.; Corminboeuf, C.; Puchta, R.; Schleyer, P. v. R., "Which NICS Aromaticity Index for Planar π Rings Is Best?," Org. Lett., 2006, 8, 863-866, DOI: 10.1021/ol0529546.

InChI

3: InChI=1/C8H4N4S/c1-2-10-6-4-8-7(11-13-12-8)3-5(6)9-1/h1-4H
4: InChI=1/C8H6N4S/c1-2-10-6-4-8-7(11-13-12-8)3-5(6)9-1/h1-4,9-10H
5: InChI=1/C8H6N4S/c1-2-10-6-4-8-7(11-13-12-8)3-5(6)9-1/h1-2H,3-4H2

We noted in Chapter 2.1 some serious errors in the prediction of bond dissociation energies using B3LYP. For example, Gilbert examined the C-C bond dissociation energy of some simple branched alkanes.¹ The mean absolute deviation (MAD) for the bond dissociation energy predicted by G3MP2 is 1.7 kcal mol^-1 and 2.8 kcal mol^-1 using MP2. In contrast, the MAD for the B3LYP predicted values is 13.7 kcal mol^-1, with some predictions in error by more than 20 kcal mol^-1. Furthermore, the size of the error increases with the size of the molecule. Consistent with this trend, Curtiss and co-workers noted a systematic underestimation of the heat of formation of linear alkanes of nearly 0.7 kcal mol^-1 per bond using B3LYP.²

Further evidence disparaging the general performance of DFT methods (and B3LYP in particular) was presented in a paper by Grimme and in two back-to-back Organic Letters articles, one by Schreiner and one by Schleyer. Grimme³ noted that the relative Energy of two C₈H₁₈ isomers, octane and 2,2,3,3-tetramethylbutane are incorrectly predicted by DFT methods (Table 1). While MP2 and CSC-MP2 (spin-component-scaled MP2) correctly predict that the more branched isomer is more stable, the DFT methods predict the inverse! Grimme attributes this error to a failure of these DFT methods to adequately describe medium-range electron correlation.

Schreiner⁵ also compared the energies of hydrocarbon isomers. For example, the three lowest energy isomers of C₁₂H₁₂ are 1-3, whose B3LYP/6-31G(d) structures are shown in Figure 1. What is disturbing is that the relative energies of these three isomers depends strongly upon the computational method (Table 2), especially since these three compounds appear to be quite ordinary hydrocarbons. CCSD(T) predicts that 2 is about 15 kcal mol^-1 less stable than 1 and that 3 lies another 10 kcal mol^-1 higher in energy. MP2 exaggerates the separation by a few kcal mol^-1. HF predicts that 1 and 2 are degenerate. The large HF component within B3LYP leads to this DFT method’s poor performance. B3PW91 does reasonably well in reproducing the CCSD(T) results.

1 xyz file

2 xyz file

3 xyz file

Figure 1. Structures of 1-3 at B3LYP/6-31G(d).

Another of Schreiner’s examples is the relative energies of the C₁₀H­₁₀ isomers; Table 3 compares their relative experimental heats of formation with their computed energies. MP2 adequately reproduces the isomeric energy differences. B3LYP fairs quite poorly in this task. The errors seem to be most egregious for compounds with many single bonds. Schreiner recommends that while DFT-optimized geometries are reasonable, their energies are unreliable and some non-DFT method should be utilized instead.

Schleyer’s example of poor DFT performance is in the isodesmic energy of Reaction 1 evaluated for the n-alkanes.⁶ The energy of this reaction becomes more positive with increasing chain length, which Schleyer attributes to stabilizing 1,3-interactions between methyl or methylene groups. (Schleyer ascribes the term “protobranching” to this phenomenon.) The stabilization energy of protobranching using experimental heats of formation increases essentially linearly with the length of the chain, as seen in Figure 2.

n-CH₃(CH₂)_mCH₃ + mCH₄ → (m + 1)C₂H₆         Reaction 1

Schleyer evaluated the protobranching energy using a variety of methods, and these energies are also plotted in Figure 2. As expected, the G3 predictions match the experimental values quite closely. However, all of the DFT methods underestimate the stabilization energy. Most concerning is the poor performance of B3LYP. All three of these papers clearly raise concerns over the continued widespread use of B3LYP as the de facto DFT method. Even the new hybrid meta-GGA functionals fail to adequately predict the protobranching phenomenon, leading Schleyer to conclude: “We hope that Check and Gilbert’s pessimistic admonition that ‘a computational chemist cannot trust a one-type DFT calculation’¹ can be overcome eventually”. These papers provide a clear challenge to developers of new functionals.

Figure 2. Comparison of computed and experimental protobranching stabilization energy (as defined in Reaction 1) vs. m, the number of methylene groups of the n-alkane chain.⁶

Truhlar believes that one of his newly developed functionals answers the call for a reliable method. In a recent article,⁴ Truhlar demonstrates that the M05-2X⁷ functional performs very well in all three of the cases discussed here. In the case of the C₈H₁₈ isomers (Table 1), M05-2X properly predicts that 2,2,3,3-tetramethylbutane is more stable than octane, and estimates their energy difference within the error limit of the experiment. Second, M05-2X predicts the relative energies of the C₁₂H₁₂ isomers 1-3 within a couple of kcal mol^-1 of the CCSD(T) results (see Table 2). Last, in evaluating the isodesmic energy of Reaction 1 for hexane and octane, M05-2X/6-311+G(2df,2p) predicts energies of 11.5 and 17.2 kcal mol^-1 respectively. These are in excellent agreement with the experimental values of 13.1 kcal mol^-1 for butane and 19.8 kcal mol^-1 for octane.

Truhlar has also touted the M05-2X functional’s performance in handling noncovalent interactions.⁸ For example, the mean unsigned error (MUE) in the prediction of the binding energies of six hydrogen-bonded dimers is 0.20 kcal mol^-1. This error is comparable to that from G3 and much better than CCSD(T). With the M05-2X functional already implemented within NWChem and soon to be released within Gaussian and Jaguar, it is likely that M05-2X may supplant B3LYP as the new de facto functional in standard computational chemical practice.

Schleyer has now examined the bond separation energies of 72 simple organic molecules computed using a variety of functionals,⁹ including the workhorse B3LYP and Truhlar’s new M05-2X. Bond separation energies are defined by reactions of each compound, such as three shown below:

The new M05-2X functional performed the best, with a mean absolute deviation (MAD) from the experimental energy of only 2.13 kcal mol^-1. B3LYP performed much worse, with a MAD of 3.96 kcal mol^-1. As noted before, B3LYP energies become worse with increasing size of the molecules, but this problem is not observed for the other functionals examined (including PW91, PBE, and mPW1PW91, among others). So while M05-2X overall appears to solve many of the problems noted with common functionals, it too has some notable failures. In particular, the error is the bond separation energies of 4, 5, and 6 is -8.8, -6.8, and -6.0 kcal mol^-1, respectively.

References

(1) Check, C. E.; Gilbert, T. M., “Progressive Systematic Underestimation of Reaction Energies by the B3LYP Model as the Number of C-C Bonds Increases: Why Organic Chemists Should Use Multiple DFT Models for Calculations Involving Polycarbon Hydrocarbons,” J. Org. Chem. 2005, 70, 9828-9834, DOI: 10.1021/jo051545k.

(2) Redfern, P. C.; Zapol, P.; Curtiss, L. A.; Raghavachari, K., “Assessment of Gaussian-3 and Density Functional Theories for Enthalpies of Formation of C₁-C₁₆ Alkanes,” J. Phys. Chem. A 2000, 104, 5850-5854, DOI: 10.1021/jp994429s.

(3) Grimme, S., “Seemingly Simple Stereoelectronic Effects in Alkane Isomers and the Implications for Kohn-Sham Density Functional Theory,” Angew. Chem. Int. Ed. 2006, 45, 4460-4464, DOI: 10.1002/anie.200600448

(4) Zhao, Y.; Truhlar, D. G., “A Density Functional That Accounts for Medium-Range Correlation Energies in Organic Chemistry,” Org. Lett. 2006, 8, 5753-5755, DOI: 10.1021/ol062318n

(5) Schreiner, P. R.; Fokin, A. A.; Pascal, R. A.; deMeijere, A., “Many Density Functional Theory Approaches Fail To Give Reliable Large Hydrocarbon Isomer Energy Differences,” Org. Lett. 2006, 8, 3635-3638, DOI: 10.1021/ol0610486

(6) Wodrich, M. D.; Corminboeuf, C.; Schleyer, P. v. R., “Systematic Errors in Computed Alkane Energies Using B3LYP and Other Popular DFT Functionals,” Org. Lett. 2006, 8, 3631-3634, DOI: 10.1021/ol061016i

(7) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., “Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(8) Zhao, Y.; Truhlar, D. G., “Assessment of Model Chemistries for Noncovalent Interactions,” J. Chem. Theory Comput. 2006, 2, 1009-1018, DOI: 10.1021/ct060044j.

(9) Wodrich, M. D.; Corminboeuf, C.; Schreiner, P. R.; Fokin, A. A.; Schleyer, P. v. R., “How Accurate Are DFT Treatments of Organic Energies?,” Org. Lett., 2007, 9, 1851-1854, DOI: 10.1021/ol070354w.

InChI

1: InChI=1/C11H10/c1-2-5-7-3(1)4(1)8-6(2)10-9(5)11(7,8)10/h1-10H

2: InChI=1/C12H12/c1-2-4-10-6-8-11-7-5-9(3-1)12(10)11/h1-12H

3: InChI=1/C12H12/c1-2-4-8-11(7-3-1)12-9-5-6-10-12/h1-12H

4: InChI=1/C6H6/c1-4-5(2)6(4)3/h1-3H2

5: InChI=1/C8H10/c1-3-7-5-6-8(7)4-2/h3-4H,1-2,5-6H2

6: InChI=1/C10H10/c1-2-8-5-6-9-4-3-7(1)10(8)9/h1-10H