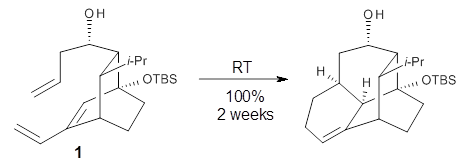
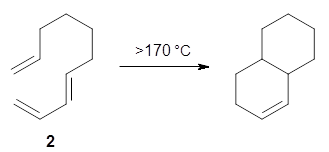
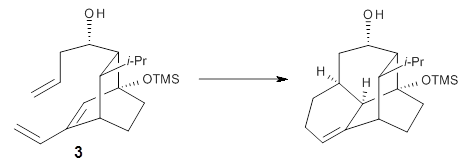
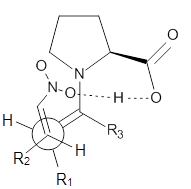
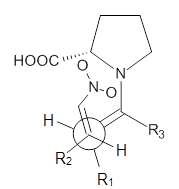
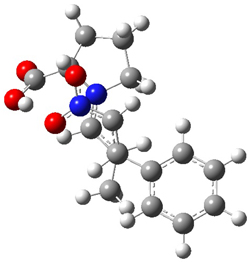
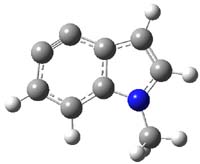
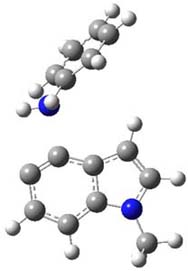
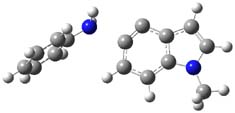
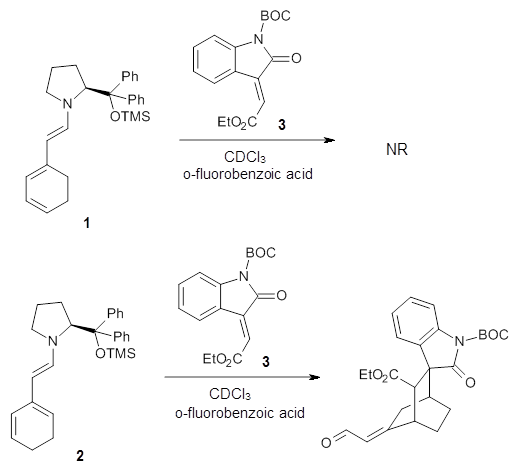
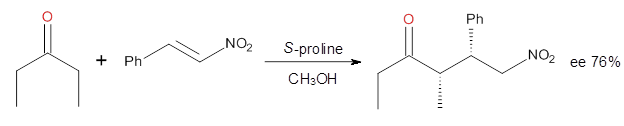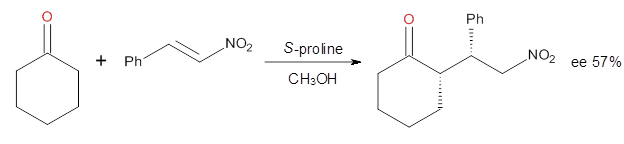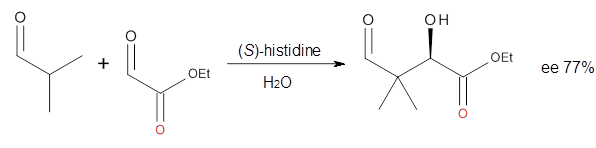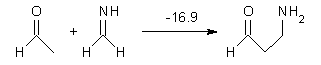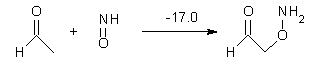Halskov, et al.¹ reported the interesting Diels-Alder selectivity shown in Scheme 1. The linear trienamine 1 did not undergo the Diels-Alder addition, while the less stable cross-conjugated diene 2 does react with 3 with high diastereo- and enantioselectivity. Their MPW1K/6-31+G(d,p) computations on a model system, carried out for a gas-phase environment, indicated a concerted mechanism, with thermodynamic control. However, the barrier for the reverse reaction for the kinetic product was computed to be greater than 30 kcal mol^-1, casting doubt on the possibility of thermodynamic control.

Scheme 1.

Houk and co-workers² have re-examined this reaction with the critical addition of performing the computation including the solvent effects. Since the stepwise alternatives involve the formation of zwitterions, solvent can be critical in stabilizing these charge-separated species, intermediates that might be unstable in the gas phase. Henry Rzepa has pointed out in his blog and on many comments in this blog about the need to include solvent, and this case is a prime example of the problems inherent in neglecting solvation.

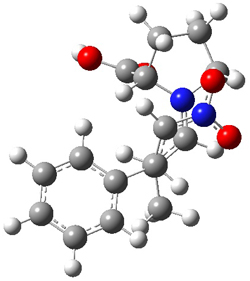
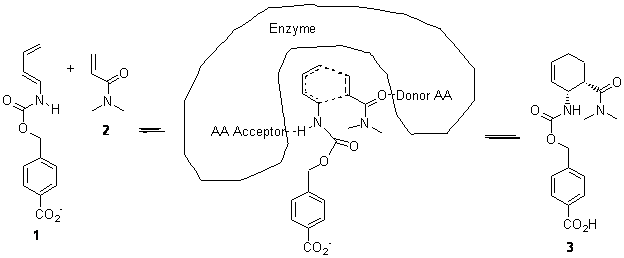
Using models of the above reaction Houk located two zwitterionic intermediates of the Michael addition for both the reactions of 4 with 6 and of 5 with 6. The second step then involves the closure of the ring to give what would be Diels-Alder products. This is shown in Scheme 2. They were unable to locate transition states for any concerted pathways. The computations were done at M06-2x/def2-TZVPP/IEFPCM//B97D/6-31+G(d,p)/IEFPCM, modeling trichloromethane as the solvent.

Scheme 2. Numbers in italics are energies relative to 4 + 6.

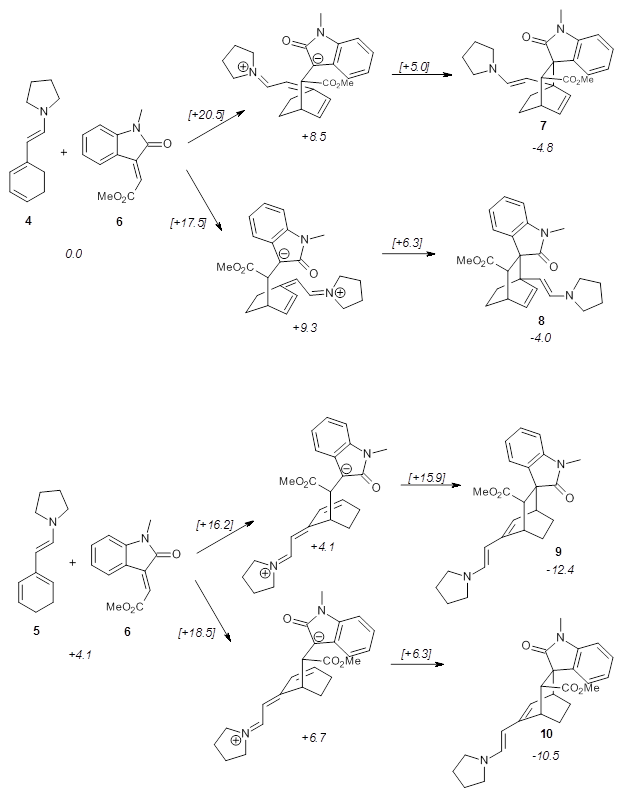
The activation barrier for the second step in each reaction is very small, typically less than 5 kcal mol^-1, so the first step is rate determining. The lowest barrier is for the reaction of 5 leading to 9, analogous to the observed product. Furthermore, 9 is also the thermodynamic product. Thus, the regioselectivity is both kinetically and thermodynamically controlled through a stepwise reaction. This conclusion is only possible by including solvent in order to stabilize the zwitterionic intermediates, and should be a word of caution for everyone doing computations: be sure to include solvent for any reactions that involved charged or charge-separated species at any point along the reaction pathway!

References

(1) Halskov, K. S.; Johansen, T. K.; Davis, R. L.; Steurer, M.; Jensen, F.; Jørgensen, K. A. "Cross-trienamines in Asymmetric Organocatalysis," J. Am. Chem. Soc. 2012, 134, 12943-12946,
DOI: 10.1021/ja3068269.

(2) Dieckmann, A.; Breugst, M.; Houk, K. N. "Zwitterions and Unobserved Intermediates in Organocatalytic Diels–Alder Reactions of Linear and Cross-Conjugated Trienamines," J. Am. Chem. Soc. 2013, 135, 3237-3242, DOI: 10.1021/ja312043g.

The intramolecular Diels-Alder reaction of 1 occurs slowly, but quantitatively, at room temperature.¹ This is unusual as most Diels-Alder cyclizations require heating to typically 200 °C. For example, the related cyclization of 2 requires heating to 170 °C.² What is the cause for this proximity-induced reaction?

Houk and Baran address this question using a computational approach.³ The Diels-Alder reaction of 2 and a simplified analogue of 1, namely 3, were computed at CPCM/M06-2x/6-311+G(d,p)//B3LYP/6-31G(d). The optimized transition states for the reaction of 2 and 3 are shown in Figure 1. The free energy of activation of 3 is 5.4 kcal mol^-1 lower in energy than the free energy of activation of 2. This is consistent with the much faster reaction of 1 than 2 observed in the experiment.

TS2

TS3

Figure 1. B3LYP/6-31G(d) for the transition states of Reactions 2 and 3.

Partitioning 3 into fragments allows Houk and Baran to apply the distortion model. They find that the rigid diene in 3 (and thereby 1) accelerates the reaction relative to the more flexible diene of 2. Further, strain relief in going from 3 (and thereby 1) to TS3 (and thereby to TS of reaction 1) and the formation of an intramolecular hydrogen bond leads to the lower activation energy of 3, and therefore of 1.

References

(1) Maimone, T. J.; Voica, A.-F.; Baran, P. S. "A Concise Approach to Vinigrol," Angew. Chem. Int. Ed. 2008, 47, 3054-3056, DOI: 10.1002/anie.200800167.

(2) Diedrich, M. K.; Klärner, F.-G.; Beno, B. R.; Houk, K. N.; Senderowitz, H.; Still, W. C. "Experimental Determination of the Activation Parameters and Stereoselectivities of the Intramolecular Diels−Alder Reactions of 1,3,8-Nonatriene, 1,3,9-Decatriene, and 1,3,10-Undecatriene and Transition State Modeling with the Monte Carlo-Jumping Between Wells/Molecular Dynamics Method," J. Am. Chem. Soc. 1997, 119, 10255-10259, DOI: 10.1021/ja9643331.

(3) Krenske, E. H.; Perry, E. W.; Jerome, S. V.; Maimone, T. J.; Baran, P. S.; Houk, K. N. "Why a Proximity-Induced Diels–Alder Reaction Is So Fast," Org. Lett. 2012, 14, 3016-3019, DOI: 10.1021/ol301083q.

InChIs

1: InChI=1S/C23H40O2Si/c1-10-12-19(24)21-20(16(3)4)18-13-14-23(21,15-17(18)11-2)25-26(8,9)22(5,6)7/h10-11,15-16,18-21,24H,1-2,12-14H2,3-9H3/t18?,19-,20?,21?,23+/m0/s1
InChIKey=NGVNTJGCNDZDEY-RHDCMTSYSA-N

2: InChI=1S/C10H16/c1-3-5-7-9-10-8-6-4-2/h3-5,7H,1-2,6,8-10H2/b7-5+
InChIKey=HXZJJSYHNPCGKW-FNORWQNLSA-N

3: InChI=1S/C20H34O2Si/c1-8-10-18(21)20(15(3)4)14-17-11-12-19(20,13-16(17)9-2)22-23(5,6)7/h8-9,13,15,17-18,21H,1-2,10-12,14H2,3-7H3/t17?,18-,19+,20?/m0/s1
InChIKey=GDQHAOHEZAJKPI-FUFFSDJGSA-N

Has there been an organic reaction more examined by computational methods than the Diels-Alder reaction? You’d think we would have covered all aspects of this reaction by now, but no, it appears that this reaction remains fertile hunting grounds.

Doubleday and Houk have examined the Diels-Alder reaction with an eye towards its synchronicity,¹ an area that Houk has delved into throughout his career. While most experiments show significant stereoselectivity, a few examples display a small amount of stereo loss. Computed transition states tend to have forming C-C bond distances that are similar, though with proper asymmetric substitution, the asymmetry of the TS can be substantial. In this paper,¹ they utilize reaction dynamics specifically to assess the time differential between the formation of the two new C-C single bonds. They examined the eight reactions shown below. The first six (R1-R6) have symmetric transition states, though with the random sampling about the TS for the initial condition of the trajectories, a majority of asymmetric starting conditions are used. The last two (R7 and R8) reactions have asymmetric TSs and the random sampling amplifies this asymmetry.

Nonetheless, the results of the dynamics are striking. The time gap, the average time between the formations of the first and second new C-C bond, for R1-R6 is less than 5 fs, much shorter than a C-C vibration. These reactions must be considered as concerted and synchronous. Even the last two reactions (R7 and R8), which are inherently more asymmetric, still have very short time gaps of 15 and 56 fs, respectively. One might therefore reasonably conclude that they too are concerted and synchronous.

There are some exceptions – a few trajectories in the last two reactions involve a long-lived (~1000 fs) diradical intermediate. At very high temperature, about 2% of the trajectories invoke a diradical intermediate. But the overall message is clear: the Diels-Alder reaction is inherently concerted and synchronous.

References

(1) Black, K.; Liu, P.; Xu, L.; Doubleday, C.; Houk, K. N. "Dynamics, transition states, and timing of bond formation in Diels–Alder reactions," Proc. Nat. Acad. Sci. USA, 2012, 109, 12860-12865, DOI: 10.1073/pnas.1209316109

Here are a couple of articles describing computational approaches to catalytic enantioselective reactions using variations upon the classic proline-catalyzed aldol reaction of List and Barbas¹ that started the whole parade. I have discussed the major computational papers on that system in my book (Chapter 5.3).

Yang and Wong² investigated the proline-catalyzed nitro-Michael reaction, looking at four examples, two with aldehydes and two with ketones (Reactions 1-4).

These four reactions were examined atMP2/311+G**//M06-2x/6-31G**, and PCM was also applied. The key element of this study is that they examined two different types of transition states: (a) based on the Houk-List model involving a hydrogen bond and (b) an electrostatic based model with no hydrogen bond. These are sketched in Scheme 1. For each of the reactions 1-4 there are 8 located transition states differing in the orientation of the attack on to the syn or anti enamine.

Scheme 1. TS models

The two lowest energy TS are shown in Figure 1. TS1-β1-RS is the lowest TS and it leads to the major enantiomer. The second lowest TS, TS1-β3-SR, lies 2.9 kJ mol^-1 above the other TS, and it leads to the minor enantiomer. This lowest TS is of the Houk-List type (Model A) while the other TS is of the Model B type. The enthalpies of activation suggest an ee of 54%, in reasonable
agreement with experiment.

TS1-β1-RS

TS1-β1-RS

Figure 1. M06-2x/6-31G** optimized geometries of TS1-β1-RS and TS1-β1-RS.

The computations of the other three reactions are equally good in terms of agreement with experiment, and importantly the computations indicate the reversal of stereoselection between the aldehydes and the ketones. These computations clearly implicate both the Houk-List and the non-hydrogen bonding TSs in the catalyzed Michael additions.

Houk in collaboration with Scheffler and Mahrwald investigate the use of histidine as a catalyst for the asymmetricaldol reaction.³ Examples of the histidine-catalyzed aldol are shown in Reactions 5-7.

	Reaction 5
	Reaction 6
	Reaction 7

The interesting twist here is whether the imidazole can also be involved in hydrogen bonding to the acceptor carbonyl group, serving the purpose of the carboxylic acid group in the Houk-List TS when proline is the catalyst (Model A). The transition states for these and a few other reactions were computed at M06-2x/6-31+G(d,p) including with the SMD continuum solvent model for water. The two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde are shown in Figure 2; TS1 has the carboxylic acid group as the hydrogen donor while the imidazole is the donor in TS2. Of note is that these two TS are isoenergetic, indicating that both modes of stabilization are at play with histidine as the catalyst.

TS1

TS2

Figure 2. M06-2x/6-31+G(d,p) geometries of the two lowest energy TSs for the reaction of isobutyraldehde and formaldehyde catalyzed by histidine.

The possible TSs for Reactions 5-7 were also located. For example, with Reaction 5, the lowest energy TS involves the imidazole as the hydrogen donor and it leads to the major product. The lowest energy TS that leads to the minor product involves the carboxylic acid as the donor. The computed ee’s for Reactions 5-7 are in very good, if not excellent, agreement with the experimental values. The study should spur further activity in which one might tune the stereoselectivity by using catalysts with multiple binding opportunities.

References

(1) List, B.; Lerner, R. A.; Barbas, C. F., III; "Proline-Catalyzed Direct Asymmetric Aldol Reactions," J. Am. Chem. Soc., 2000, 122, 2395-2396, DOI: 10.1021/ja994280y.

(2) Yang, H.; Wong, M. W. "(S)-Proline-catalyzed nitro-Michael reactions: towards a better understanding of the catalytic mechanism and enantioselectivity," Org. Biomol. Chem.,
2012, 10, 3229-3235, DOI: 10.1039/C2OB06993H

(3) Lam, Y.-h.; Houk, K. N.; Scheffler, U.; Mahrwald, R. "Stereoselectivities of Histidine-Catalyzed Asymmetric Aldol Additions and Contrasts with Proline Catalysis: A Quantum Mechanical Analysis," J. Am. Chem. Soc. 2012, 134, 6286-6295, DOI: 10.1021/ja2118392

One of the great challenges to computational chemistry and computational biochemistry is rational design of enzymes. Baker and Houk have been pursuing this goal and in their recent paper they report progress towards an enzyme designed to catalyze a Diels-Alder reaction.¹

They envisaged an enzyme that could catalyze the Diels-Alder of 1 with 2 by having a suitable hydrogen bond acceptor of the carbamide proton of 1 (such as the carbonyl oxygen of glutamine or asparagine) along with a suitable donor to the oxygen of 2 (such as the hydroxyl of tyrosine, serine or threonine) – as shown below. Along with positioning the diene and dienophile near each other and properly orienting them for reaction, the activation barrier should be lowered by narrowing the HOMO-LUMO gap.

A series of transition states for the Diels-Alder reaction of 1 with 2 along with the hydrogen-bonded amino acids were optimized B3LYP/6-31+G(d,p) and used as constraints within the RosettaMatch code for locating a protein scaffold that could accommodate this TS structure. This resulted in 84 protein designs, each of which were synthesized and screened for activity in catalyzing the Diels-Alder reaction. Of these potential enzymes, 50 were soluble and of these 50, only 2 showed any activity. These two were selectively mutated to try to improve activity, and some improvement was obtained.

Of particular note is that mutation that removed one or both of the residues designed to hydrogen bond to the substrates resulted in complete loss of activity.

In principle 8 different steriosomeric products are possible in the reaction of 1 with 2. In solution in the absence of enzyme, four products are observed, with the major product (47%) the 3R,4S endo prodcut 3. The designed enzymes were constructed to make this product, and in fact it is the only observed stereoisomer formed in the reaction in the presence of enzyme. Furthermore, the designed enzymes are quite selective; for example, changing a single N-methyl group to N-ethyl on 2 reduced the rate by a factor of 2 and larger substituents resulted in a greater rate suppression.

Turnover rate is high and suggests that these enzymes might have real application in chemical synthesis. The disappointing aspect of the study was the poor ratio of predicted enzymes (84) to ones that actually had activity (2).

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D., "Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239

In a follow-up to their experimental study that found that cyclobutenone is an excellent dienophile (and which I blogged about here), Danishefsky teams up with Houk and provides an insight into the reactivity.¹ In the Diels-Alder reaction of cyclopentadiene with 2-cyclohexenone, 2-cyclopentenone and cyclobutenone, the product yield increases in the order 36%, 50% and 77%. M06-2x activation enthalpies decrease in this series 15.0, 13.3 and 10.5 kcal mol^-1.

While these activation energies do not correlate with reaction energies, the activation energies do correlate nicely with the distortion energy. (Distortion energy is the energy required to distort reactants to their geometries in the transition state, but without their interaction.) Houk and Danishefsky argue that it is much easier to distort cyclobutenone to its geometry in the TS (and this distortion is primarily moving the alkenyl hydrogens out of plane, away from the incoming diene) than for the larger rings. This is due to (a) the larger s-character of the C-H bond in the smaller ring and (b) the C-C-C angle in the smaller ring is closer to the angle in the pyramidalized TS structure.

References

(1) Paton, R. S.; Kim, S.; Ross, A. G.; Danishefsky, S. J.; Houk, K. N., "Experimental Diels–Alder Reactivities of Cycloalkenones and Cyclic Dienes Explained through Transition-State Distortion Energies," Angew. Chem. Int. Ed., 2011, 44, 10366–10368, DOI: 10.1002/anie.201103998

The de novo design of catalysts for specific purposes remains an inspired goal for chemists and biochemists. Ken Houk and David Baker have been pursuing this goal, and their recent paper on the design of a catalyst for the bimolecular Diels-Alder¹ is a real significant step forward.

Their model enzyme is one that will provide a hydrogen bond acceptor to the carbamate proton of 1 and a proton donor to the carbonyl oxygen of the amide 2. This model is sketched in Figure 1. Glutamine or asparagines will serve as the acceptor and serine, threonine, or tyrosine will serve as the proton donor. The catalytic site is then modeled, and then this active site is fit within 207 protein scaffolds. About 10¹⁹ active site configurations are reduced to about 10⁶ possible protein scaffolds. Optimization of these led to 84 protein designs.

Figure 1. Enzyme model

These 84 possible proteins were then synthesized within E. coli and then tested for catalytic behavior
in the Diels-Alder reaction of 1 + 2. Only 2 enzymes have activity, and with some protein modifications, quite reasonable enzyme activity is found. These enzymes show strong selectivity for the substrates – addition of a methyl group significantly diminishes catalytic activity. Perhaps most important is that of the 8 possible isomers that can be formed (4 isomers are produced in the uncatalyzed reaction) only 1 is produced here, the 3R,4S isomer 3.

All-in-all, a quite remarkable accomplishment!

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D.,
"Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239.

InChIs

1: InChI=1/C13H13NO4/c1-2-3-8-14-13(17)18-9-10-4-6-11(7-5-10)12(15)16/h2-8H,1,9H2,(H,14,17)(H,15,16)/p-1/b8-3+/fC13H12NO4/h14H/q-1
InChIKey=HGMJQUSLRHRARW-OSXKDGDFDJ

2: InChI=1/C5H9NO/c1-4-5(7)6(2)3/h4H,1H2,2-3H3
InChIKey=YLGYACDQVQQZSW-UHFFFAOYAD

3: InChI=1/C18H22N2O5/c1-20(2)16(21)14-5-3-4-6-15(14)19-18(24)25-11-12-7-9-13(10-8-12)17(22)23/h4,6-10,14-15H,3,5,11H2,1-2H3,(H,19,24)(H,22,23)/p-1/t14-,15+/m0/s1/fC18H21N2O5/h19H/q-1
InChIKey=WWWDBAXWGWLFSD-AFFTYDCXDH

Houk and Doubleday have a nice follow-up study¹ to their previous MD study² of 1,3-dipolar cycloadditions, which I posted on here. They report on the cycloaddition of either acetylene or ethylene to 9 different 1,3-dipoles. Continuing on Houk’s recent thread of looking at distortion energies to attain the TS, they note that a sizable fraction (often over 50%) of the distortion energy is associated with bending the X-Y-Z bond of the dipole, consistent with their earlier work suggesting the importance of this vibration in attaining and crossing the TS. What’s new in this paper is the extensive MD studies, with trajectory studies of all 18 reactions. These revealed again the importance of vibrational energy in this X-Y-Z bending mode in crossing the TS. They also noted the role of translational energy, and the relationship between translational vs. vibrational energy depending on the early/late nature of the TS. Their final point was that the lifetime of any diradical or diradical-like intermediate is so short, less than the time of a bond vibration, so that one can discount any diradical participation. The reaction is concerted.

References

(1) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloadditions: Energy Partitioning of Reactants and Quantitation of Synchronicity," J. Am. Chem. Soc., 2010, ASAP, DOI: /10.1021/ja909372f

(2) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloaddition Reactions of Diazonium Betaines to Acetylene and Ethylene: Bending Vibrations Facilitate Reaction," Angew. Chem. Int. Ed., 2009, 48, 2746-2748, DOI: 10.1002/anie.200805906

The nature of reactions of indolynes is the subject of two recent computational/experimental studies. There are three isomeric indolynes 1a-c which are analogues of the more famous benzyne (which I discuss in significant detail in Chapter 4.4 of my book).

One might anticipate that the indolynes undergo comparable reactions as benzyne, like Diels-Alder reactions and nucleophilic attack. In fact the indolynes do undergo these reactions, with unusual regiospecificity. For example, the reaction of the substituted 6,7-indolyne undergoes regioselective Diels-Alder cycloaddition with substituted furans (Scheme 1), but the reaction with the other indolynes gives no regioselection. ¹ Note that the preferred product is the more sterically congested adduct.

Scheme 1

In the case of nucleophilic addition, the nucleophiles add specifically to C₆ with substituted 6,7-indolynes (Scheme 2), while addition to 4,5-indolynes preferentially gives the C₅-adduct (greater than 3:1) while addition to the 5,6-indolynes preferentially gives the C₅-adduct), but with small selectivity (less than 3:1).²

Scheme 2

The authors of both papers – Chris Cramer studied the Diels-Alder chemistry and Ken Houk studied the nucleophilic reactions – employed DFT computations to examine the activation barriers leading to the two regioisomeric products. So for example, Figure 1 shows the two transition states for the reaction of 2c with 2-iso-propyl furan computed at MO6-2X/6-311+G(2df,p).

ΔG‡ = 9.7

ΔG‡ = 7.6

Figure 1. MO6-21/6-311+G(2df,p) optimized TSs for the reaction of 2-iso-propylfuran with 2c. Activation energy (kcal mol^-1) listed below each structure.¹

The computational results are completely consistent with the experiments. For the Diels-Alder reaction of 2-t-butylfuran with the three indolynes 2a-c, the lower computed TS always corresponds with the experimentally observed major product. The difference in the energy of the TSs leading to the two regioisomers for reaction with 2a and 2b is small (less than 1 kcal mol^-1), consistent with the small selectivity. On the other hand, no barrier could be found for the reaction of 2-t-butylfuran with 2c that leads to the major product. Similar results are also obtained for the nucleophilic addition – in all cases, the experimentally observed major product corresponds with the lower computed activation barrier.

So what accounts for the regioselectivity? Both papers make the same argument, though couched in slightly different terms. Houk argues in terms of distortion energy – the energy needed to distort reactants to their geometries in the TS. As seen in Figure 2, the benzyne fragment of 2a is distorted, with the C-C-C angle at C₄ of 125° and at C₅ of 129°. In the transition states, the angle at the point of nucleophilic attack widens. Since the angle starts out wider at C₅, attack there is preferred, since less distortion is needed to achieve the geometry of the TS.

2a
TS at C4 ΔG‡ = 12.9	TS at C5 ΔG‡ = 9.9

Figure 2. B3LYP/6-31G(d) optimized structures of 2a and the TSs for the reaction of aniline with 2a. Activation energy in kcal mol^-1.²

Cramer argues in terms of the indolyne acting as an electrophile. Increasing substitution at the furan 2-position makes is better at stabilizing incipient positive charge that will build up there during a (very) asymmetric Diels-Alder transition state. This explains the increasing selectivity of the furan with increasing substitution. The indolyne acting as an electrophile means that the attack will lead from the center will lesser charge. In 2c, the C-C-C angle at C₆ is 135.3°, while that at C₇ is 117.2°. This makes C₇ more carbanionic and C₆ more carbocationic; therefore, the first bond made is to C₆, leading to the more sterically congested product. Note that Houk’s argument applies equally well, as C₆ is predistorted to the TS geometry.

References

(1) Garr, A. N.; Luo, D.; Brown, N.; Cramer, C. J.; Buszek, K. R.; VanderVelde, D., "Experimental and Theoretical Investigations into the Unusual Regioselectivity of 4,5-, 5,6-, and 6,7-Indole Aryne Cycloadditions," Org. Lett., 2010, 12, 96-99, DOI: 10.1021/ol902415s

(2) Cheong, P. H. Y.; Paton, R. S.; Bronner, S. M.; Im, G. Y. J.; Garg, N. K.; Houk, K. N., "Indolyne and Aryne Distortions and Nucleophilic Regioselectivites," J. Am. Chem. Soc., 2010, 132, 1267-1269, DOI: 10.1021/ja9098643

InChIs

1a: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h2,4-6,9H
InChIKey=RNDHGGYOIRREHC-UHFFFAOYAU

1b: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h3-6,9H
InChIKey=WWZQFJXNXMIWCD-UHFFFAOYAO

1c: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h1,3,5-6,9H
InChIKey=UHIRLIIPIXHWLT-UHFFFAOYAH

2a: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h3,5-7H,1H3
InChIKey=VTVUPAJGRVFCKI-UHFFFAOYAJ

2b: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h4-7H,1H3
InChIKey=KKPOWDDYMOXTFW-UHFFFAOYAN

2c: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h2,4,6-7H,1H3
InChIKey=MDAHOGWZOBLIEX-UHFFFAOYAZ

Houk has performed a very nice examination of the performance of some density functionals.¹ He takes a quite different approach than what was proposed by Grimme – the “mindless” benchmarking² using random molecules (see this post). Rather, Houk examined a series of simple aldol, Mannich and α-aminoxylation reactions, comparing their reaction energies predicted with DFT against that predicted with CBQ-QB3. The idea here is to benchmark DFT performance for simple reactions of specific interest to organic chemists. These reactions are of notable current interest due their involvement in organocatalytic enantioselective chemistry (see my posts on the aldol, Mannich, and Hajos-Parrish-Eder-Sauer-Wiechert reaction). Examples of the reactions studied (along with their enthalpies at CBS-QB3) are Reaction 1-3.

For the four simple aldol reactions and four simple Mannich reactions, PBE1PBE,
mPW1PW91 and MO6-2X all provided reaction enthalpies with errors of about 2 kcal mol^-1. The much maligned B3LYP functional, along with B3PW91 and B1B95 gave energies with significant larger errors. For the three α-aminoxylation reactions, the errors were better with B3PW91 and B1B95 than with PBE1PBE or MO6-2X. Once again, it appears that one is faced with finding the right functional for the reaction under consideration!

Of particular interest is the decomposition of these reactions into related isogyric, isodesmic
and homdesmic reactions. So for example Reaction 1 can be decomposed into Reactions 4-7 as shown in Scheme 1. (The careful reader might note that these decomposition reactions are isodesmic and homodesmotic and hyperhomodesmotic reactions.) The errors for Reactions 4-7 are typically greater than 4 kcal mol^-1 using B3LYP or B3PW91, and even with MO6-2X the errors are about 2 kcal mol^-1.

Scheme 1.

Houk also points out that Reactions 4, 8 and 9 (Scheme 2) focus on having similar bond changes as in Reactions 1-3. And it’s here that the results are most disappointing. The errors produced by all of the functionals for Reactions 4,8 and 9 are typically greater than 2 kcal mol^-1, and even MO2-6x can be in error by as much as 5 kcal mol^-1. It appears that the reasonable performance of the density functionals for the “real world” aldol and Mannich reactions relies on fortuitous cancellation of errors in the underlying reactions. Houk calls for the development of new functionals designed to deal with fundamental simple bond changing reactions, like the ones in Scheme 2.

Scheme 2

References

(1) Wheeler, S. E.; Moran, A.; Pieniazek, S. N.; Houk, K. N., "Accurate Reaction Enthalpies and Sources of Error in DFT Thermochemistry for Aldol, Mannich, and α-Aminoxylation Reactions," J. Phys. Chem. A 2009, 113, 10376-10384, DOI: 10.1021/jp9058565

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, 5, 993–1003, DOI: 10.1021/ct800511q