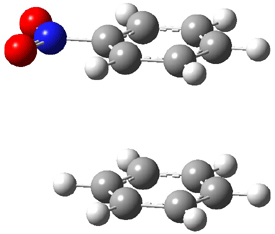
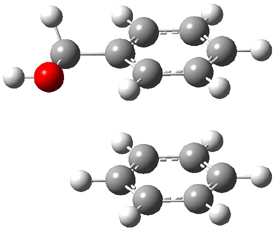
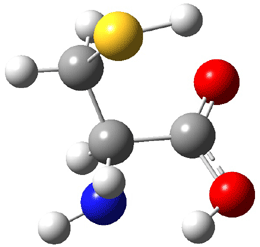
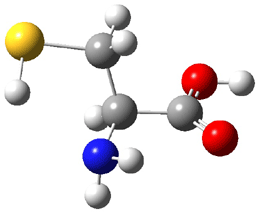
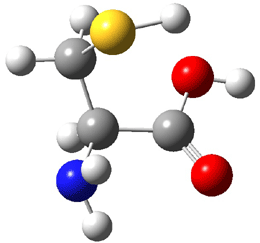
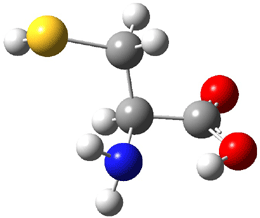
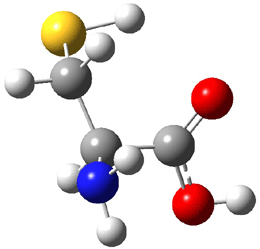
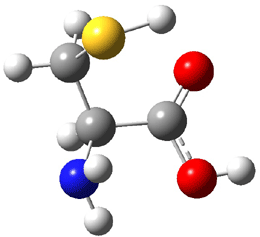
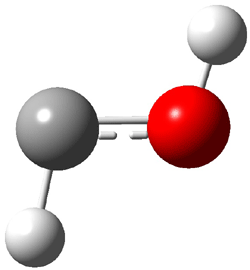
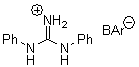
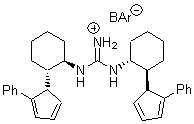
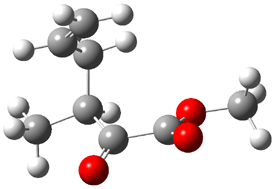
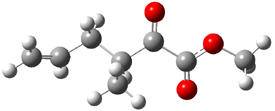
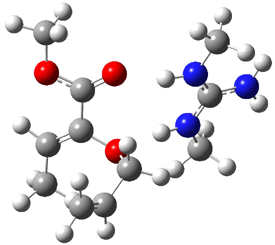
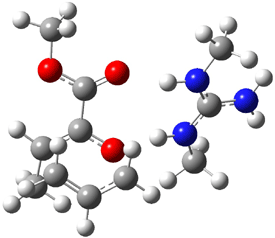
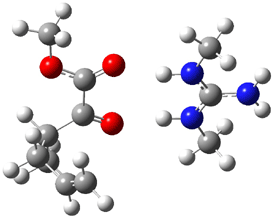
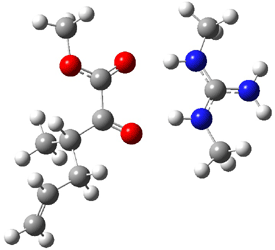
An alternative take on the nature of the interaction in π-stacking is offered by Wheeler and Houk.¹ They start by examining the binding between benzene and a series of 24 substituted benzenes. Two representative dimmers are shown in Figure 1, where the substituent is NO₂ or CH₂OH. As was noted in a number of previous studies,^2-6 the binding with any substituted benzene is stronger than the parent benzene dimer. Nonetheless, Wheeler and Houk point out that the binding energy has a reasonable correlation with σ_m. It appears that the benzene dimer itself is the outlier; the binding energy when the substituent is CH₂OH, whose σ_m value is zero, is bound more tightly than the benzene dimer. They conclude that there is a dispersive interaction between any substituent and the other benzene ring.

(a)	(b)
(c)	(d)

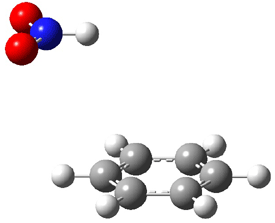
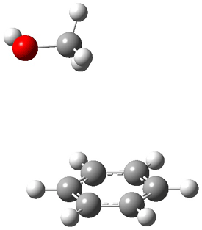
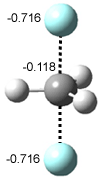
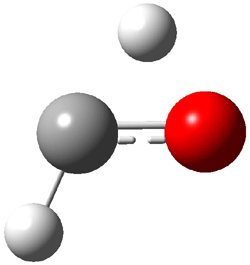
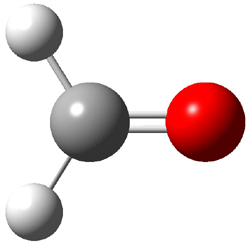
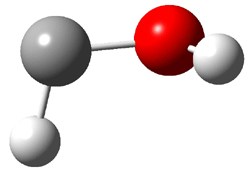
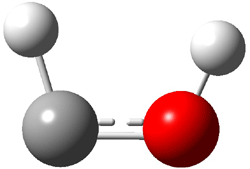
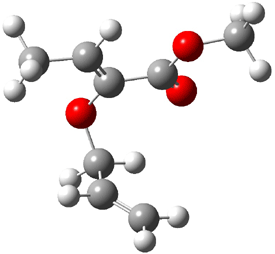
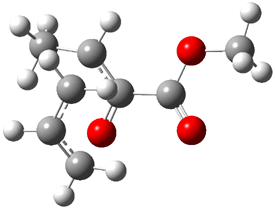
Figure 1. MO5-2X/6-31+G(d) optimized geometries of (a) C₆H₆-C₆H₅NO₂, (b) C₆H₆-C₆H₅CH₂OH, (c) C₆H₆-HNO₂, and (d) C₆H₆-HCH₂OH.¹

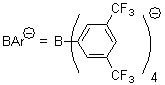
They next constructed an admittedly very crude model system whereby the substituted benzene C₆H₅X is replaced by HX; the corresponding models are also shown in Figure 1. The binding energies of these model dimmers correlates very well with the real dimmers, with r = 0.91. Rather than involving the interaction of the π-electrons, the origin of the enhanced binding in aromatic dimers involves electrostatic interactions of the substituent with the other aromatic ring – effectively the quadrupole of the unsubstituted ring interacts with the dipoles of the substituent and its ring system. In addition, the inherent dispersive interaction increase the binding.

References

(1) Wheeler, S. E.; Houk, K. N., "Substituent Effects in the Benzene Dimer are Due to Direct Interactions of the Substituents with the Unsubstituted Benzene," J. Am. Chem. Soc., 2008, 130, 10854-10855, DOI: 10.1021/ja802849j.

(2) Sinnokrot, M. O.; Sherrill, C. D., "Unexpected Substituent Effects in Face-to-Face π-Stacking Interactions," J. Phys. Chem. A, 2003, 107, 8377-8379, DOI: 10.1021/jp030880e.

(3) Sinnokrot, M. O.; Sherrill, C. D., "Substituent Effects in π-&pi Interactions: Sandwich and T-Shaped Configurations," J. Am. Chem. Soc., 2004, 126, 7690-7697, DOI: 10.1021/ja049434a.

(4) Sinnokrot, M. O.; Sherrill, C. D., "Highly Accurate Coupled Cluster Potential Energy Curves for the Benzene Dimer: Sandwich, T-Shaped, and Parallel-Displaced Configurations," J. Phys. Chem. A, 2004, 108, 10200-10207, DOI: 10.1021/jp0469517

(5) Lee, E. C.; Kim, D.; Jurecka, P.; Tarakeshwar, P.; Hobza, P.; Kim, K. S., "Understanding of Assembly Phenomena by Aromatic-Aromatic Interactions: Benzene Dimer and the Substituted Systems," J. Phys. Chem. A 2007, 111, 3446-3457, DOI: 10.1021/jp068635t.

(6) Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C., "Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of
(bio)organic molecules," Org. Biomol. Chem. 2007, 741-758, DOI: 10.1039/b615319b

I have an immediate opening in my group for a post-doctoral associate. The position involves computational approaches to a variety of problems, including nucleophilic substitution at heteroatoms, solvent effects, and host-guest chemistry. The candidate must have some experience with computational chemistry, especially with any one of the major ab initio programs (like Gaussian, or Gamess or NWChem, etc.).

If you are interested in the position, please see the description here.

Angewandte Chemie has published a rather unusual short article – an appeal by Roald Hoffmann, Paul Schleyer and Fritz Schaefer (the latter two were interviewed in my book!) to use “more realism, please!”¹

These noted computational chemists suggest that we all have been sloppy in the language we use in describing our computations. They first take on the term “stable”, and rightfully point out that this is a very contextual term – stable where? on my desktop? In a 1M aqueous solution? Inside a helium glove box? Inside a mass spectrometer? In an interstellar cloud? Stable for how long? Indefinitely? For a day? For a day in the humid weather of San Antonio? Or a day inside a cold refrigerator? Or how about inside a Ne matrix? Or for the time it takes to run a picosecond laser experiment?

The authors offer up the terms “viable” and “fleeting” as reasonable alternatives and proscribe a protocol for meeting the condition of “viable” – and I must note that this protocol is very demanding, likely beyond the computational abilities of many labs and certainly beyond what can be done for a reasonably large molecule.

They also take on the uncertainty of computed results, pointing out the likely largely overlooked irreproducibility of many DFT results, due to size difference of the computed grids, difference in implementation of the supposedly same functional, etc. They conclude with a discussion of how many significant figures one should employ.

None of this is earth-shattering, and most is really well-known yet often neglected or overlooked. In another interesting publication treat in this issue, four referee reports of the article are reproduced. The first, by Gernot Frenking,² argues exactly this point – that the lack of new information, and the sort of whimsical literary approach make the article unacceptable for publication. The other three referees disagree,^3-5 and note that though the article is not novel, the authors forcefully remind us that better behaviors should be put into practice.

The article is a nice reminder that careful studies should be carefully reported. (And both the authors of the article and the referees note that these same comments apply to our experimental colleagues, too.)

References

(1) Hoffmann, R.; Schleyer, P. v. R.; Schaefer III, H. F., “Predicting Molecules – More Realism, Please!,” Angew. Chem. Int. Ed., 2008, 47, 7164-7167, DOI: 10.1002/anie.200801206.

(2) Frenking, G., “No Important Suggestions,” Angew. Chem. Int. Ed. 2008, 47, 7168-7169, doi: 10.1002/anie.200802500.

(3) Koch, W., “Excellent, Valuable, and Entertaining,” Angew. Chem. Int. Ed., 2008, 47, 7170, DOI: 10.1002/anie.200802996.

(4) Reiher, M., “Important for the Definition of Terminology in Computational Chemistry,” Angew. Chem. Int. Ed., 2008, 48, 7171, DOI: 10.1002/anie.200802506.

(5) Bickelhaupt, F. M., “Attractive and Convincing,” Angew. Chem. Int. Ed., 2008, 47, 7172, DOI: 10.1002/anie.200802330.

Schaefer and Allen have applied their focal point method to the question of the benzylic effect in the S_N2 reaction.¹ S_N2 reactions are accelerated when the attack occurs at the benzylic carbon, a well-known phenomenon yet the reason for this remains unclear. The standard textbook-like argument has been that the negative charge built up in the S_N2 transition state can be delocalized into the phenyl ring. However, solution phase Hammett studies are often U-shaped, indicating that both electron donating and withdrawing group accelerate the substitution reaction. (This is usually argued as indicative of a mechanism change from S_N2 to S_N1.)

The focal point method involves a series of very large computations where both basis set size and degree of electron correlation are systematically increased, allowing for an extrapolation to essentially infinite basis set and complete correlation energy. The energy of the transition state (relative to separated reactants) for four simple S_N2 reactions evaluated with the focal point method are listed in Table 1. The barrier for the benzylic substitutions is lower than for the methyl cases, indicative of the benzylic effect.

Table 1. Energy (kcal mol^-1) of the transition state relative to reactants.¹

To answer the question of why the benzylic substitution reactions are faster, they examined the charge distribution evaluated at B3LYP/DZP++. As seen in Table 1, this method does not accurately reproduce the activation barriers, but the errors are not terrible, and the trends are correct.

In Figure 1 are the geometries of the transition states for the reaction of fluoride with methylflouride or benzylfluoride. The NBO atomic charges show that the phenyl ring acquired very little negative charge at the transition state. Rather, the electric potential at the carbon under attack is much more revealing. The potential is significantly more positive for the benzylic carbon than the methyl carbon in both the reactant and transition states.

VC = -405.156 V	VC = -404.379 V

Figure 1. MP2/DZP++ transition states for the reaction of fluoride with methylfluoride and benzylflouride. NBO charges on F and C and the electrostatic potential in Volts.¹

They next examined the reaction of fluoride with a series of para-substituted benzylfluorides. The relation between the Hammet σ constants and the activation energy is fair (r = 0.971). But the relation between the electrostatic potential at the benzylic carbon (in either the reactant or transition state) with the activation energy is excellent (r = 0.994 or 0.998). Thus, they argue that it is the increased electrostatic potential at the benzylic carbon that accounts for the increased rate of the S_N2 reaction.

References

(1) Galabov, B.; Nikolova, V.; Wilke, J. J.; Schaefer III, H. F.; Allen, W. D., "Origin of the S_N2 Benzylic Effect," J. Am. Chem. Soc., 2008, 130, 9887-9896, DOI: 10.1021/ja802246y.

A nice summary of the tunneling behavior of hydroxymethylene¹ was just published by Bucher in Angewandte Chemie.² Bucher strongly points out that the really novel part of this work is the very large barrier through which the proton tunnels. My blog post on this topic is here.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard IV, F. C.; Simmonett, A. C.; Allen, W.
D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

(2) Bucher, G.; “Hydroxycarbene: Watching a Molecular Mole at Work,” Angew. Chem. Int. Ed., 2008, 47, 6957 – 6958, DOI: 10.1002/anie.200803195

Alonso and coworkers have developed the technique of laser ablation molecular beam Fourier transform microwave spectroscopy to detect biomolecules. In a recent paper¹ they determined the structure of the glycine:one water complex – it is of the neutral configuration. They have now examined the conformations of cysteine². The presence of the thiol side group adds considerable complexity to the problem due to the many conformations possible.

The experiment detected six conformers. Determining the structures responsible for each set of signals was made possible by comparing the experimental results with those determined by computation. Alonso computed 11 low energy conformations of cysteine at MP2/6-311++G(d,p). Then comparing the computed rotational constants and ¹⁴N nuclear quadrupole coupling tensor components with the experiment, they were able to match up all six experimental conformers with computed structures. The experimental and computed constants for the three most abundant structures are listed in Table 1. The geometries of all six conformers are drawn in Figure 1.

Table 1.Experimental and computed spectroscopic constants (MHz) for the three most abundant conformers of cysteine.²

^aRelative energy in cm^-1 computed at MP4/6-311++G(d,p)// MP2/6-311++G(d,p).

IIb (0.0)	Ia (450)
Ib (325)	IIa (527)
IIIβc (765)	IIIβb (585)

Table 1. Optimized structures of the six observed conformers of cysteine. Relative energies in cm^-1 computed at MP4/6-311++G(d,p)//MP2/6-311++G(d,p). (Note – the geometries shown were optimized at PBE1PBE/6-311+G(d,p) since they MP2 structures are not available!)

This study demonstrates the nice complementary manner in which computation and experiment can work together in structure determination.

References

(1) Alonso, J. L.; Cocinero, E. J.; Lesarri, A.; Sanz, M. E.; López, J. C., "The Glycine-Water
Complex," Angew. Chem. Int. Ed. 2006, 45, 3471-3474, DOI: 10.1002/anie.200600342

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, DOI: 10.1002/anie.200801337

InChI

Cysteine: InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

The very simple carbene hydroxymethylene, HOCH, has finally been prepared and characterized.¹ Glyoxylic acid CHOCO₂H is subjected to high-vacuum laser photolysis. It fragments into HOCH, which is then trapped into an argon matrix. The experimental IR frequencies match up very well with the CCSD(T)/cc-pVQZ harmonic frequencies of the trans isomer 1t that are also adjusted for anharmonic effects. The computed vertical excitation energy of 415 nm matches well with the experimental value of the maximum absorption in the UV/vis spectra of 427 nm.

The other very interesting experimental result is that HOCH has a lifetime of about 2 hours in the matrix, while the deuterated species DOCH is stable. To explain these results, Schreiner, Allen and co-workers optimized a number of structures on the PES at CCSD(T)/cc-pVQZ and computed their energies using the focal point technique. The optimized structures and their relative energies are given in Figure 1.

1t (0.0)	TS2 (29.7)	2 (-52.1)
TS1(26.8)
1c (4.4)

Figure 1. Optimized CCSD(T)/cc-pVQZ structures of HOCH isomers and their Focal Point relative energies (kcal mol^-1).¹

The barriers for rearrangement from 1t are both very high. Rearrangement to formaldehyde 2 requires crossing a barrier of 29.7 kcal mol^-1, while the barrier to convert to the cis isomer 1c is 26.8 kcal mol^-1. (Note that from 1c a cleavage into CO and H2 can occur, but this barrier is another 47.0 kcal mol^-1.) These barriers are too large to be crossed at the very low temperatures of the matrices. However, using the intrinsic reaction potential at CCSD(T)/cc-pVQZ and WKB theory, the tunneling lifetime of HOCH is computed to be 122 minutes, in excellent accord with the experiment. The lifetime for DOCH is computed to be over 1200 years. Thus, the degradation of hydroxymethylene is entirely due to tunneling through a very large classical barrier! This rapid tunneling casts serious doubt on the ability to ever identify any hydroxymethylene in interstellar space.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard IV, F. C.; Simmonett, A. C.; Allen, W.
D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

InChI

1: InChI=1/CH2O/c1-2/h1-2H
2: InChI=1/CH2O/c1-2/h1H2

Here is another review of my book Computational Organic Chemistry; DOI: 10.1002/aoc.1406. This one is by John Brazier James Platts of Cardiff University and it appears in Applied Organometallic Chemistry. I do plead guilty to the charge of the interviews being USA-centric. This was due to scheduling problems that did not allow me to travel overseas.

Addicoat and Mehta¹ have made a modification of the “Kick” algorithm. Recall, that the Kick method (discussed in this previous blog post) takes a collection of atom coordinates and applies a random kick to each atom. This creates a new initial configuration and a geometry optimization is performed starting form this configuration. If hundreds of such configurations are chosen, one hopes to locate most if not all reasonable structures. The new variation is to create fragments in which the atoms are held fixed. Then the kick is applied to the fragment as a whole.

Among the examples demonstrated in the paper, only one is of an organic species. They examined the structure of the Gly-Trp peptide associated with two water molecules. They used two conformations of the Gly-Trp dipeptide. The kick was supplied to one of these conformers and to the two water molecules. They ended up locating 22 structures with the first conformer and 46 with the second, spanning a range of about 0.5 eV. It must be pointed out that many of these configurations are clearly noncompetitive by not maximizing the degree of hydrogen bonding that can be obtained. Furthermore, many other conformers of the dipeptide would need to be examined to really map out the full PES and definitively locate all reasonable low-energy configurations. (it is not necessary that the gas-phase low-energy conformers yield the lowest energy configurations of the water complex.) Nonetheless, this modified kick procedure offers a “quick-and-dirty” means of generating a wide variety of initial conditions for locating structures.

References

(1) Addicoat, M. A.; Metha, G. F., "Kick: Constraining a Stochastic Search Procedure with Molecular Fragments," J. Comput. Chem., 2008, DOI: 10.1002/jcc.21026

There remains still new territory to explore even with such well-known reactions as the Claisen rearrangement. Jacobsen reports a catalyzed Claisen rearrangement where the catalyst is urea-based.¹ Catalyst 1 produces modest to very reasonable % conversion in a series of simple Claisen rearrangements, as shown in Table 1.

Table 1. Claisen Rearrangements

With the chiral catalyst 2, the Claisen rearrangement is both catalyzed and proceeds with large enantiomeric excess, as shown in the representative example Reaction 1.

Jacobsen and Uyeda also reported the transition state for a model Claisen rearrangement catalyzed by a model guanidinium ion (Reaction 2) computed at B3LYP/6-31G(d). I have reproduced this calculation and the calculations for the both the catalyzed and uncatalyzed rearrangements, shown in Figure 1. In email communication with Dr. Jacobsen, I was able to confirm these energies against their own unpublished results.

Uncatalyzed Reaction 2
Reactant: 0.0	TS: 25.73
Product 1: -11.04	Product 2: -13.69
Catalyzed Reaction 2
Reactant: 0.0	TS: 21.09
Product 1: -12.36	Product 2: -12.80

Figure 1. B3LYP/6-31G(d) optimized structures of the critical points of uncatalyzed and catalyzed Reaction 2. Relative energies in kcal mol^-1.

The structures show the beneficial hydrogen bonds between the guanidinium anion and the carbonyl oxygens (or the ether oxygen of the reactant). In progressing from the transition state, both reactions first gives Product 1. This product conformer can than rotate to give the lower energy conformer Product 2. The activation energy of the catalyzed reaction is 4.64 kcal mol^-1 lower than for the uncatalyzed reaction, demonstrating the benefit of the complexation in the transition state.

I want to thank Dr. Jacobsen and his graduate student Chris Uyeda for sharing their computational results with me for the preparation of this blog post.

References

(1) Uyeda, C.; Jacobsen, E. N., "Enantioselective Claisen Rearrangements with a Hydrogen-Bond Donor Catalyst," J. Am. Chem. Soc., 2008, 130, 9228-9229, DOI: 10.1021/ja803370x.