Jacobsen has been pioneering the use of small organic molecules as catalysts where the interaction between the substrate and catalyst is non-covalent. At the 2009 Welch Conference last week, he spoke about the use of amido-thiourea catalysts in the enantioselective Strecker reaction. This post discusses how computations were used to determine the mechanism and helps explain the enantioselectivity.
The thiourea 1 was found to be the best catalyst for the hydrocyanation of imines. An example of this catalysis is Reaction 1. The system is quite tolerant to changes of the group attached to the carbon of the imine: with R = t-butyl group, the yield is 99% with an enantiomeric excess of 93% and with a phenyl group, the yield is 98% with 98% ee.1
|
|
Reaction 1 |
In a follow-up article, Jacobsen employs a nice combination of experiments and DFT computations to shed light on the mechanism.2 Kinetic studies established that the rate of the hydrocyanation is first order in HCN, imine and catalyst. This suggested two possible mechanisms, Scheme 1a (where protonation of the imine is followed by formation of the C-CN bond) and Scheme 1b (where cyanide adds first, followed by protonation).
Scheme 1.
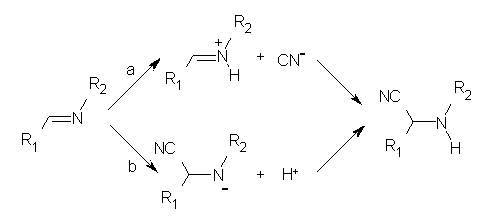
A Hammett study of phenyl-substituted imines indicates a negative ρ value, indicative of positive charge build up on nitrogen, suggesting the mechanism shown in Scheme 1a. Now on the computations!
A model study was first performed at B3LYP/6-31G(d) for the reaction of HCN with imine 2a with the catalyst 3a. Three complexes involving the three species of nearly equivalent energy were found. The first mechanism examined is for direct addition of cyanide to imine with the catalyst activating the imine. This pathway was identified but it has a very high barrier (46 kcal mol-1) and the rates of the urea and thiourea-catalyzed reactions are nearly identical, but the computations for this mechanism suggest that the thiourea-catalyzed reaction should be substantially faster. This mechanism can be discounted.

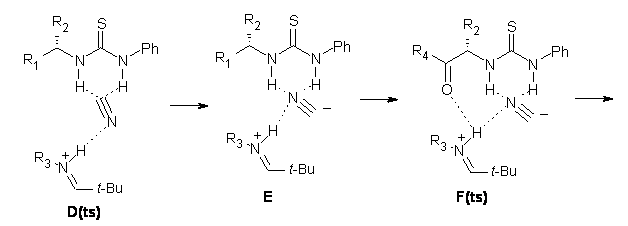
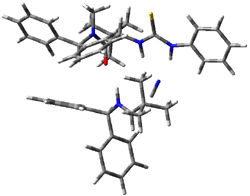
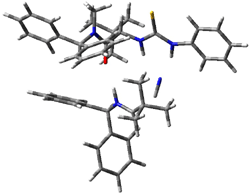
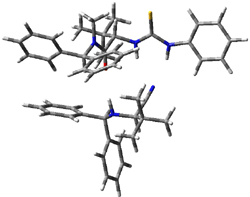
Next, they examined two related mechanism whereby either HCN or HNC complex to the catalysts and then transfer their proton to the imine. This is followed by cyanide attack on the protonated imine. The reaction involving HNC is slightly lower than that of HCN, and so this mechanism is pursued further with catalyst 3b, which more closely mimics the true catalyst, and imine 2b. The lowest energy pathway for the addition of HCN to 2b with catalyst 3b is schematically shown in Scheme 2. From A to E is transfer of the proton from HNC to the imine and rotation of the CN anion. The highest barrier is through TS F, which involves moving the imine over to the carbonyl group. The last step is the attack of the cyanide group. The structures of E through I are shown in Figure 1.
Scheme 2
|
|
|
|
|
|
|
E |
F |
|
G |
H |
|
I |
|
Figure 1. B3LYP/6-31G(d) optimized geometries for steps along Scheme 2.
The step involving the transition state F is rate determining. They then computed the difference in the activation barrier through TS F for a variety of different imines using the R– and S-catalyst and compared that with the experimental enantioselectivity. These turn out to correlate extremely well, suggesting that in fact the enantioselectivity is discriminated through TS F! And the structural feature that best correlates with this enantioselectivty is the sum of the O…H and N…H distances in F for the R– and S-catalysts. So it is the ability to stabilize the iminium cation that is key.
A couple of caveats: first, the potential energy surface of this reaction is quite complex – Jacobsen suggests a pathway with 9 critical points. One might imagine that there could be other pathways and other important critical points, and fully characterizing this surface would be an enormous task! The nice agreement between the computations and the available experiments do give the computed pathway some credence. Second, the reactions are run in solution, and solvent has been neglected in these computations. Given that charge-separated species are being formed, solvent could be a factor. Nonetheless, this remains an interesting set of papers as it shows how computations are now a standard tool even amongst synthetic chemists!
References
(1) Zuend, S. J.; Coughlin, M. P.; Lalonde, M. P.; Jacobsen, E. N., "Scaleable catalytic asymmetric Strecker syntheses of unnatural α-amino acids," Nature, 2009, 461, 968-970, DOI: 10.1038/nature08484.
(2) Zuend, S. J.; Jacobsen, E. N., "Mechanism of Amido-Thiourea Catalyzed Enantioselective Imine Hydrocyanation: Transition State Stabilization via Multiple Non-Covalent Interactions," J. Am. Chem. Soc. 2009, 131, 15358-15374, DOI: 10.1021/ja9058958.




Henry Rzepa responded on 04 Nov 2009 at 7:00 am #
As usual from the Jacobsen school, this is superb stuff.
I would like to also draw attention to another computational investigation of the asymmetric Strecker, this time using Aluminium cyanide as the reagent. This was in fact elaborated a few years back as part of a lecture course I give entitled case studies in molecular modelling, and here it served two purposes.
Firstly, an existing mechanism is evaluated computationally. It soon emerges that it is deficient
A modification to the standard mechanism also emerges with deficiencies, in particular due to the failure to consider the entropies of the process (which in effect kill that mechanism).
Inspiration is sought from the Cambridge crystal structure database
With this information, a new mechanism is proposed, which in fact replicates both the enantioselectivity, and the substituent effects on the kinetics.
I think it is certainly true nowadays that no report of a reaction where the mechanism is speculated upon should be published without a computational exploration of whether that mechanism is viable, and indeed whether it fits the known facts. Let’s face it, for a period of perhaps 30-40 years, it was assumed a sine qua non that any new reaction should be accompanied by mechanistic speculation as to its course (the curly arrow pushing proof). If reasonable arrows could be pushed, the mechanism was accepted, albeit rarely with kinetic or other direct experimental proof. In retrospect, many of these curly-arrow mechanisms have been found wanting when subjected to quantitative quantum mechanical scrutiny.
I work in predominantly a synthetic chemistry department, where curly arrow pushing reigned supreme until recently. Now increasingly, colleagues approach us to test their mechanistic hypotheses. It is not unusual for us to come back to them a week or so later with the definitive declaration that one or more of their mechanistic pathways appears not viable. Often, better ones can be substituted. In this sense, mechanistic chemistry, having been founded in firm experimental practice of kinetic measurement, went through a long period where speculation (often wild) was permissible, but now I think we are entering the next phase where such speculation must be backed up by proper quantum mechanical exploration of the potential energy surface. I would argue that the majority of new reported reactions should in future have this component, and that they should be rejected for publication if they do not!
As noted elsewhere on Steve’s blog, the same applies to spectroscopic assignments! But that is a different thread.
Henry Rzepa responded on 05 Nov 2009 at 1:17 am #
The final paragraph of Steve’s blog on this item discusses the neglect of solvation on the mechanistic pathway. He is absolutely correct of course. Take a look for example at DOI 10.1039/b913295c for a particularly relevant case where two mechanistic pathways are mooted, but one has far more charge separation than the other. A simple test (which as a referee I always insist the authors of articles apply) is to report the dipole moments. In the example I quoted earlier, the two alternative transition states had dipole moments of ~6D and ~12D. Even in a solvent such as dichloromethane, a solvation correction can invert the energies of these two systems.
The difficulty with correcting for solvation in the past has been evaluating what effect the solvent has on the geometry of the species involved. Cavity-based solvation methods work by tesselating the cavity into small triangles. This can have the unfortunate effect that evaluating derivatives for such functions can lead to irregular or even discontinuous behaviour, which in turn makes geometry optimization non-convergent. Fortunately, Darrin York and Martin Karplus came to the rescue (some time ago, it has to be said, DOI: 10.1021/jp992097l) by formulating a smoothed out solvation cavity where the first (and second derivatives) are stable and well behaved. Well, I can report in this comment to Steve’s blog (you saw it here first!) that this makes a spectacular difference to our ability to study reaction mechanisms with solvation fields. There now truly is absolutely no reason why solvated and properly optimized reaction transition states cannot become standard. We have applied this principle to the last mechanism we have studied, and it was truly effective (but apologies, I will not be blogging this research on this occasion!). Indeed, if anyone reading this blog also referees journal articles, and you come across an article where solvation is not included, send the article back to its authors with a request to do so before accepting it for publication!
Let me make an even stronger statement! With this enhancement to the computational chemist’s armory, it must be now an essential requirement to investigate the potential surface of any reaction where a serious attempt is being made to propose a mechanism for it. Lack of solvation methodology is no longer an excuse!
Computational Organic Chemistry » Enantioselective Michael Addition responded on 21 Dec 2009 at 9:26 am #
[…] computational/experimental study of the enantioselective Strecker reaction by Jacobsen (see this post), there’s this JACS communication that really disappoints in its use of computational chemistry. […]