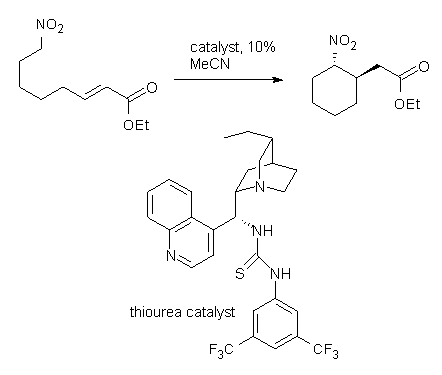
Coming on the heels of the very nice combined computational/experimental study of the enantioselective Strecker reaction by Jacobsen (see this post), there’s this JACS communication that really disappoints in its use of computational chemistry. Cobb uses yet another chiral thiourea to produce the enantioselective intramolecular Michael addition of nitronoates (Reaction1).1 The reaction goes with excellent diastereoselectivity and eneatioselectivity, and can even be done with a substrate to produce three chiral centers. This is very nice synthetic chemistry.
|
|
Reaction 1. dr >19:1 |
The lack of reactivity of the Z ester suggested that the thiourea must associate with both the nitro group and the ester carbonyl. The authors provide a B3LYP/3-21G complex of thiourea with a simple nitroester (once again without providing coordinates in the supporting materials!) to demonstrate this sort of association. But this single structure, at this very low computational level, with these simplified reagents, and lacking solvent (see Rzepa’s comment) really makes one wonder just what value this computation provides. It also goes to demonstrate just how much effort Jacobsen went through to provide substantive computational support for his proposed mechanism of action.
References
(1) Nodes, W. J.; Nutt, D. R.; Chippindale, A. M.; Cobb, A. J. A., "Enantioselective Intramolecular Michael Addition of Nitronates onto Conjugated Esters: Access to Cyclic γ-Amino Acids with up to Three Stereocenters," J. Am. Chem. Soc. 2009, 131, 16016-16017, DOI: 10.1021/ja9070915

Henry Rzepa responded on 27 Dec 2009 at 5:16 am #
There is an increasing realization that modelling enantioselective complexes is far more, well complex, than many a modeller realizes. Put it this way, if you perform an Bader AIM calculation on the putative transition state or complex aspiring to explain stereoselectivity, you are likely to get a dazzling array of so called BCPs, or bond critical points. The key property of these points is the value of ρ(r (and possibly also the Laplacian). The value for conventional bonds is in the region of 0.2-0.4, but below that threshold, there are many critical points that occur down to a value of 0.005. It seems agreed that below this threshold, the interaction is now “noise”. But this zoo of points in the region say 0.005 to 0.02 must signify something! But what is that something? Some of these points are probably “repulsive”, the point having been created by enforced proximity of two atoms. But many others are certainly “attractive”. We give them names such as “hydrogen bonds” or “π-stacking”, or quite often simply “dispersion” or “Van-der-Waals attractions”. These are the isotopic ones; then there are the anisotropic interactions! A typically complex (i.e.large) active site for an enantioselective reaction may have let’s say about 10-20 such “interactions”, and the specificity is (in part) the sum of all these.
One could argue that the theory of “chemical bonding” is in crisis! Many of the “interactions” responsible for stereoselectivity have no common name, and we are not even sure whether we can trust eg AIM to identify the key ones properly. If we are reduced to simply counting 10-20 interactions in a typical transition state, and guessing the outcome, then crisis is a true description. In fact, I do want to end on a more positive note. I do believe this menagerie can be sorted, and that analysis of this kind WILL become increasingly common in mechanistic articles (well I would say that in the knowledge that we have one such article in preparation at the moment!).