In a previous post, I described the work of Singleton on a simple hydroboration reaction. He found less regioselectivity than predicted by transition state theory. Further, trajectory computations suggested that dynamic effects were at play, and that some non-selective fast reactions were leading to the lower regioselection.

Pilling offers an alternative explanation based solely on RRKM (statistical) theory.¹ (Actually what is utilized is the stochastic energy grained master equation.) What he suggests is that there are hot intermediates (formed of a loose associate of BH₃ with propene) that react non-selectively before cooling. The cooled intermediates react very selectively (around 99%) to give the anti-Markovnikov product.

The upshot is that hydroboration – and by implication a whole lot of other seemingly ordinary chemistry – may in fact be much more complicated than we had previously thought. Standard transition state theory may not always apply, and trajectory analysis may not be enough!

References

(1) Glowacki, D. R.; Liang, C. H.; Marsden, S. P.; Harvey, J. N.; Pilling, M. J., "Alkene Hydroboration: Hot Intermediates That React While They Are Cooling," J. Am. Chem. Soc., 2010, 132, 13621-13623, DOI: 10.1021/ja105100f

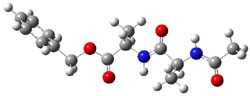
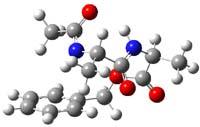
Earlier this year, Barboiu made the astonishing claim of the x-ray characterization of 1,3-dimethylcyclobutadiene, brought about by the photolysis of 4,6-dimethyl-α-pyrone encapsulated in a guanidinium-sulfonate-calixarene crystal (Reaction 1).¹ I had not blogged on this paper because Henry Rzepa did a quite thorough analysis of it in this blog post. Now, a couple of rebuttals have appeared and it is time to examine this study.

Alabugin calls in question whether the reaction has in fact proceeded beyond 2.² They note that in the x-ray crystal structure, the distance between a carbon of the purported cyclobutadiene ring and the carbon of CO₂ is only 1.50 and 1.61 Å. Barboiu called this a “strong van der Waals contact”, but this is a distance much more attributable to a covalent bond. In fact, the shorter distance is in fact shorter than some of the other C-C distances in the structure that Barboiu calls covalent! Perhaps more bizarre is that the putative CO₂ fragment is highly bent: 119.9&;deg;, a value inconsistent with CO₂ but perfectly ordinary for an sp² carbon.  In fact, B3LYP/6-31G** computations suggest that bending CO₂ this much costs about 75 kcal mol^-1 – and tack on another 7 kcal mol^-1 to make the two C-O distances unequal (as found in the x-ray structure!). Thus, Alabugin suggests that only 2 has been formed, and notes that the cleavage to 3 would likely require light of much higher energy that that used in the Barboiu experiment.

Scheschkewitz argues that the x-ray data can be better interpreted as suggesting only the Dewar β-lactone 2 is present, though in its two enantiomeric forms.³ There is no evidence, he suggests of any cyclobutadiene component at all.

It should be noted that Barboiu stands⁴ by his original work and original assignment, claiming that these types of x-ray experiments are quite difficult and large error bars in atom positions are inherent to the study.

Henry Rzepa has blogged again on this controversy and has a paper coming out on this soon. I shall update when it appears. Henry notes in one of the comments to his blog that a TD-DFT computations does show that the Dewar β-lactone 2 is transparent from 320-500nm.

References

(1) Legrand, Y.-M.; van der Lee, A.; Barboiu, M., "Single-Crystal X-ray Structure of 1,3-Dimethylcyclobutadiene by Confinement in a Crystalline Matrix," Science 2010, 329, 299-302, DOI: 10.1126/science.1188002.

(2) Alabugin, I. V.; Gold, B.; Shatruk, M.; Kovnir, K., "Comment on "Single-Crystal X-ray Structure of 1,3-Dimethylcyclobutadiene by Confinement in a Crystalline Matrix"," Science, 330, 1047, DOI: 10.1126/science.1196188.

(3) Scheschkewitz, D., "Comment on "Single-Crystal X-ray Structure of 1,3-Dimethylcyclobutadiene by Confinement in a Crystalline Matrix"," Science 2010, 330, 1047, DOI: 10.1126/science.1195752.

(4) Legrand, Y.-M.; van der Lee, A.; Barboiu, M., "Response to Comments on "Single-Crystal X-ray Structure of 1,3-Dimethylcyclobutadiene by Confinement in a Crystalline Matrix"," Science, 330, 1047, DOI: 10.1126/science.1195846.

InChIs

1: InChI=1/C7H8O2/c1-5-3-6(2)9-7(8)4-5/h3-4H,1-2H3
InChIKey=IXYLIUKQQQXXON-UHFFFAOYA

2: InChI=1/C7H8O2/c1-4-3-7(2)5(4)6(8)9-7/h3,5H,1-2H3
InChIKey=GLYAMHMFKKLRAL-UHFFFAOYAT

3: InChI=1/C6H8/c1-5-3-6(2)4-5/h3-4H,1-2H3
InChIKey=ADQGKIKNUMJFSL-UHFFFAOYAU

Heathcock’s model for predicting the stereo-outcome of Michael additions¹ involves a metal bridging across the two carbonyl oxygens. For Reaction 1, the model predicts that 1,2-syn product over the 1,2-anti product based on more favorable steric arrangements in TSA relative to TSB. Note that other rotatamers of these TS models are possible, but are presumed to be less favorable due to the inability of the metal cation to bridge the carbonyls. In fact, the syn:trans ratio for Reaction 1 is 95:5.

Kwan and Evans have examined this (and related) reactions at the M05-2x/6-31G(d) level.² Dimethyl ether is used as the model for the solvent. The lowest energy transition state for Reaction 1 is TS1, shown in Figure 1 with suppressed drawing of the hydrogens (though the JMol active image will include the hydrogens). This structure is actually more like TSC, a rotamer that was thought to not have a bridging metal. TS1 does have the bridging metal, and this is accomplished by having dihedral values of 40° instead of the ideal 60°. So, computations support the general conclusion of the Heathcock approach, with a modification of the possible inclusion of some other rotamers, though the stereoprediction is not altered.

TS1

Figure 1. M05-2x/6-31G(d) optimized structure of the lowest energy transition state of Reaction 1. Hydrogens are removed in the image for clarity, but the Jmol active image (which you can see by clicking on the above image) will include the hydrogen atoms.

References

(1) Oare, D. A.; Heathcock, C. H. In Topics in Stereochemistry; Eliel, E. L., Wilen, S. H., Eds.; Wiley: New York, 1989; Vol. 19, p 227-408.

(2) Kwan, E. E.; Evans, D. A., "Intermolecular Michael Reactions: A Computational Investigation," Org. Lett. 2010, 12, 5124–5127, DOI: 10.1021/ol102017v

The much publicized failure of common DFT methods to accurately describe alkane isomer energy and bond separation reactions (which I have blogged about many times) has recently been attributed to long-range exchange¹ (see this post) or simply just DFT exchange² (see this post). Grimme now responds by emphatically claiming that it is a failure in accounting for medium-range electron correlation.³

First, Grimme notes that the bond separation energy for linear alkanes (as defined in
Reaction 1) is underestimated by HF, and slightly overestimated by MP2, but SCS-MP2 provides energy in nice agreement with CCSD(T)/CBS energies. Since MP2 adds in coulomb correlation to the HF energy (which treats exchange exactly within a one determinant wavefunction), the traditional wavefunction approach strongly suggests a correlation error.

CH₃(CH₂)_mCH₃ + mCH₄ → (m+1)CH₃CH₃        Reaction 1

Next, bond separation energies computed with PBE and BLYP (which lack exact exchange), PBE0 (which has 25% non-local exchange) and BHLYP (which has 50% non-local exchange) are all similar and systematically too small. So, exchange cannot be the culprit. It must be correlation.

He also makes two other interesting points. First, inclusion of a long-range correction – his recently proposed D3 method⁴ – significantly improves results, but the bond separation energies are still underestimated. It is only with the double-hybrid functional B2PLYP and B2GPPLYP that very good bond separation energies are obtained. And these methods do address the medium-range correlation issue. Lastly, Grimme notes that use of zero-point vibrational energy corrected values or enthalpies based on a single conformation are problematic, especially as the alkanes become large. Anharmonic corrections become critical as does inclusion of multiple conformations with increasing size of the molecules.

References

(1) Song, J.-W.; Tsuneda, T.; Sato, T.; Hirao, K., "Calculations of Alkane Energies Using Long-Range Corrected DFT Combined with Intramolecular van der Waals Correlation," Org. Lett., 2010, 12, 1440–1443, DOI: 10.1021/ol100082z

(2) Brittain, D. R. B.; Lin, C. Y.; Gilbert, A. T. B.; Izgorodina, E. I.; Gill, P. M. W.; Coote, M. L., "The role of exchange in systematic DFT errors for some organic reactions," Phys. Chem. Chem. Phys., 2009, DOI: 10.1039/b818412g.

(3) Grimme, S., "n-Alkane Isodesmic Reaction Energy Errors in Density Functional Theory Are Due to Electron Correlation Effects," Org. Lett. 2010, 12, 4670–4673, DOI: 10.1021/ol1016417

(4) Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H., "A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu," J. Chem. Phys., 2010, 132, 154104, DOI: 10.1063/1.3382344.

Annulenes can twist, and I have blogged about a number of examples (cations and neutrals). The twist can be portioned into a twist associated with the dihedral angle as one progresses around the compound and writhe which is associated with distortion of the annulene into a third dimension.¹

Herges has prepared the 36-annulene 1 where the anthracenyl units were introduced to force the loop out of plane.² Four different conformations of 1 where isolated by crystallization out of different solvents. 1a and 1b were produced in benzene, and they differ by having two half-twists (L_k=2) and one half-twist (L_k=1), respectively. 1c was isolated from DMF, with one half-twist. 1d was isolated from Et₂O/CH₂Cl₂.

Computations at the B3LYP/6-31g* level identified 10 low lying conformations, and the ones corresponding to the experimentally observed forms are shown in Figure 1. The computed conformer that matches with 1d differs form the experimental version by a rotation about one single bond, and the computed version has a different topology than the experiment. One item of note is that all of the 10 computed conformers are dominated by the twist (T_w) and have very small writhe.

1a	1b
1c	1d
1e

Figure 1. B3LYP/6-31G* optimized structures of 1a-e.

Though not isolated in experiment, one of the low lying conformers has three half-twists (L_k=3) and is also shown in Figure 1 as 1e. Identification of this highly twisted species would be quite interesting.

References

(1) Fowler, P. W.; Rzepa, H. S., "Aromaticity rules for cycles with arbitrary numbers of half-twists," Phys. Chem. Chem. Phys., 2006, 8, 1775-1777, DOI: 10.1039/b601655c.

(2) Mohebbi, A.; Mucke, E. K.; Schaller, G.; Köhler, F.; Sönnichsen, F.; Ernst, L.; Näther, C.; Herges, R., "Singly and Doubly Twisted [36]Annulenes: Synthesis and Calculations," Chem. Eur. J., 2010, 16, 7767-7772, DOI: 10.1002/chem.201000277,

InChIs

1: InChI=1/C80H52/c1-9-25-65-57(17-1)73-45-41-53-33-35-54(36-34-53)42-46-75-61-21-5-13-29-69(61)79(70-30-14-6-22-62(70)75)51-52-80-71-31-15-7-23-63(71)76(64-24-8-16-32-72(64)80)48-44-56-39-37-55(38-40-56)43-47-74-59-19-3-11-27-67(59)78(68-28-12-4-20-60(68)74)50-49-77(65)66-26-10-2-18-58(66)73/h1-52H/b45-41-,46-42+,47-43-,48-44+,50-49+,52-51-,53-41-,54-42-,55-43-,56-44-,73-45-,74-47-,75-46-,76-48-,77-49-,78-50+,79-51+,80-52+
InChIKey=KXWPWHPRFOXOIX-IFDMNBDGBZ

Computing anions have long been understood to offer interesting challenges. For example, anions require diffuse functions for reasonable description. Jensen¹ has now investigated the electron affinity of atoms and small molecules with three DFT methods: BHHLYP having 50% HF and 50% Becke exchange, B3LYP having 20% HF and 80% Becke exchange and BLYP with 100% Becke exchange. The result is that all three express varying degrees of electron loss from the atom or molecule in the anion. Thus the anionic species really possess only fractional anionic charge.

In cation-anion pairs or in large species that have strong electron acceptors and donors (say a protein), this electron loss manifests itself in less ionic character than what should actually be present. In other words density is erroneously moved off of the anionic center and transferred to the cationic center.

This error is due to poor description of the long-range exchange. Including the LC correction does eliminate the problem, and so one should be very careful in using DFT for anions.

References

(1) Jensen, F., "Describing Anions by Density Functional Theory: Fractional Electron Affinity," J. Chem. Theory Comput., 2010, 6, 2726-2735, DOI: 10.1021/ct1003324

Borden predicted measurable heavy-atom isotope effects in the ring opening of cyclopropylcarbinyl radical. In my blog post on this paper, I concluded with the line:

Borden hopes that experimentalists will reinvestigate this
problem (and hopefully confirm his predictions).

Well, in a recent paper where Borden collaborates with Singleton, these predictions are confirmed!¹

There is a sizable kinetic isotope effect for breaking the ring bond to a ¹²C over a bond to a ¹³C atom, up to 16% at -100 °C. The KIE predicted without including tunneling are dramatically below the experimental values, but incorporation of tunneling in the computated KIEs match up with experiment with an error no greater that 0.7%. The Arrhenius plot of ln KIE vs. 1/T shows enhanced isotope effects when tunneling is included, very nice agreement between the experimental and tunneling-corrected KIEs and curvature – all indicative of heavy atom tunneling. Lastly, the ring open product (1-butene) is the observed major product (62%) at -100 °C; the minor product is methylcyclopropane. In the absence of heavy-atom tunneling, 1-butene would be the minor product (28%).

References

(1) Gonzalez-James, O. M.; Zhang, X.; Datta, A.; Hrovat, D. A.; Borden, W. T.; Singleton, D. A. J. Am. Chem. Soc., 2010, 132, 12548-12549, DOI: 10.1021/ja1055593.

InChIs

Cyclopropylcarbonyl radical: InChI=1/C4H7/c1-4-2-3-4/h4H,1-3H2
InChIKey=RMCDUNHIVVEEDD-UHFFFAOYAR

1-butene: InChI=1/C4H8/c1-3-4-2/h3H,1,4H2,2H3
InChIKey=VXNZUUAINFGPBY-UHFFFAOYAZ

I have had a long-standing interest in organolithium compounds, dating back to my graduate student days. Thus, I was excited to read Kass and Radom’s latest work on the computational and experimental evaluation of the acidity of lithium acetylide LiCCH.¹

The gas phase experimental acidity is accomplished by preparing the conjugate base of lithium acetylide through a procedure of collision-induced dissociation with loss of CO₂, as in Scheme 1. By reacting this anion with a variety of different acids, they were able to bracket the acidity and determine that ΔH_acid is 391.0 ± 1.3 kcal mol^-1. This is about 13 kcal mol^-1 less acidic than acetylene itself. The reduction is acidity understandable in terms of the C-Li being essentially ionic, and thereby loss of the proton builds up negative charge on a carbon adjacent to a carbon that already has a great deal of negative charge.

Scheme 1

Computations support this enthalpy for deprotonation. The G3, G4 and W1 values for the enthalpy deprotonation of lithium acetylide are 389.1, 388.9, and 390.4 kcal mol^-1, respectively. It should also be noted that the conjugate base of lithium acetylide posses a non-classical bridging geometry 1, which is well-known for organolithium species.²

References

(1) Meyer, M. M.; Chan, B.; Radom, L.; Kass, S., R., "Gas-Phase Synthesis and Reactivity of Lithium Acetylide Ion, LiCC^–," Angew. Chem. Int. Ed., 2010, 49, 5161-5164, DOI: 10.1002/anie.201001485

(2) Streitwieser, A.; Bachrach, S. M.; Dorigo, A.; Schleyer, P. v. R. In Lithium Chemistry: A Theoretical and Experimental Overview; Sapse, A.-M., Schleyer, P. v. R., Eds.; Wiley-Interscience: New York, 1995, p 1-45.

Here’s a nice example of the productive interplay between experiment and computations.¹ The dipeptide N-Acyl-Ala-Ala-Benzyl was prepared and subjected to UV and IR/UV analysis. The IR showed two separate structures with distinctly different environments for the NH bonds: one structure showed intramolecular hydrogen bonding while the other did not.

B97/TZVPP computations revealed two structures. The first is a linear dipeptide with intramolecular hydrogen bonding occurring in a 5,5 relationship. (There are actually three conformers of this but all have similar energy, only one is shown in Figure 1.) The second structure displays a bent shape with a NH-π interaction, also shown in Figure 1. The computed vibrational spectra for each structure matches up well with the NH region of the experimental IR.

Figure 1. B97-D/TZVPP optimized structures of N-Acyl-Ala-Ala-Benzyl.

The authors spend a great deal of time noting that the 0 K energies predict that the second structure, being 4 kcal mol^-1 more stable, should be the only one observed. However, since the jet cooling will likely trap the structures at their 300 K distribution, this could account for the existence of two structures. However, when the computations include entropy corrections, so now we’re looking at ΔG(200 K), B97-D and MO6-2x suggest that the two structures are very close in energy. But they caution that MP2 predicts a large energy gap unless atomic counterpoise corrections are used to account for intramolecular basis set superposition (see this post), a problem that appears to be much less severe with the DFT methods.

References

(1) Gloaguen, E.; de Courcy, B.; Piquemal, J. P.; Pilme, J.; Parisel, O.; Pollet, R.; Biswal, H. S.; Piuzzi, F.; Tardivel, B.; Broquier, M.; Mons, M. J. Am. Chem. Soc, 2010, 132, 11860-11863, DOI: 10.1021/ja103996q

InChIs

InChI=1/C15H20N2O4/c1-10(16-12(3)18)14(19)17-11(2)15(20)21-9-13-7-5-4-6-8-13/h4-8,10-11H,9H2,1-3H3,(H,16,18)(H,17,19)/t10-,11-/m0/s1/f/h16-17H
InChIKey=KRIKKPGWLXOEAS-VFIKCTIADD

The proline-catalyzed aldol reaction is discussed in Chapter 5.3 of my book. This is an area of continued research and the recent paper of Sharma and Sunoj addresses an alternative mechanism involving oxazolidinone.¹ They examine the proline-catalyzed aldol self-condensation of propanal with B3LYP/6-31+G** and MP2/6-31+G** computations. This reaction is found to proceed² with 4:1 anti:syn diastereoselectivity.

An oxazolidinone intermediate has been observed in proline-catalyzed aldol condensations. This intermediate is proposed to come about via Path b, whereas the generally accepted mechanism put forth by Houk and List, discussed in my book, follows Path a. Sharma and Sunoj find that the oxazolidinone 7 is lower in energy than the enamine 4, and its barrier for ring opening back to 3 is large. Thus, it is not unreasonable that it is the observed intermediate.

Gas phase computations of the reaction of 4 to 5 predict a 99% ee and an anti:syn ratio of about 5:1, in nice agreement with experiment. However, incorporation of solvent reduces the ration to 2:1, and the MP2 computations give a ratio of 1.2:1, in even worse agreement with experiment. However, the major predicted product has the same absolute configuration as the observed product.

The other mechanism is examined in the key step 8 to 9. Here all computations predict that syn addition is favored over anti addition and the enantiomer of the experimentally observed product is predicted to be formed. In addition, intermediate 9 and the TSs leading to it are much higher in energy than intermediate 5 and the TSs associated with its formation. Thus, the oxazolidinone addition mechanism is discounted.

References

(1) Sharma, A.; Sunoj, R., "Enamine versus Oxazolidinone: What Controls Stereoselectivity in Proline-Catalyzed Asymmetric Aldol Reactions?," Angew. Chem. Int. Ed., 2010, 49, 6373-6377, DOI: 10.1002/anie.201001588

(2) Northrup, A. B.; MacMillan, D. W. C., "The First Direct and Enantioselective Cross-Aldol Reaction of Aldehydes," J. Am. Chem. Soc., 2002, 124, 6798-6799, DOI: 10.1021/ja0262378