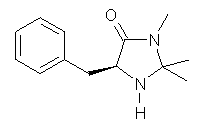
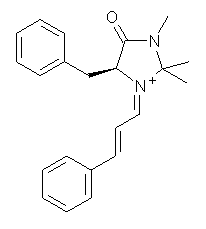
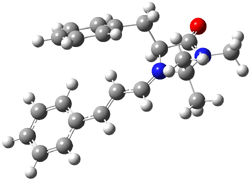
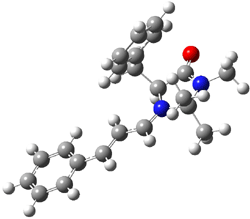
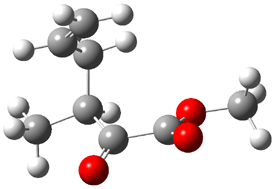
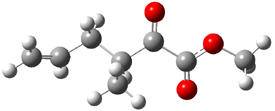
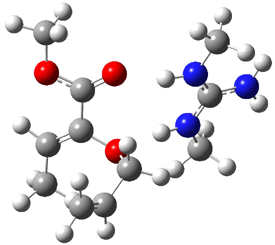
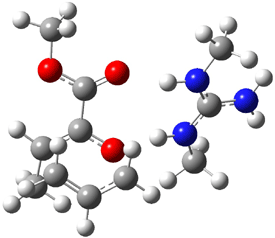
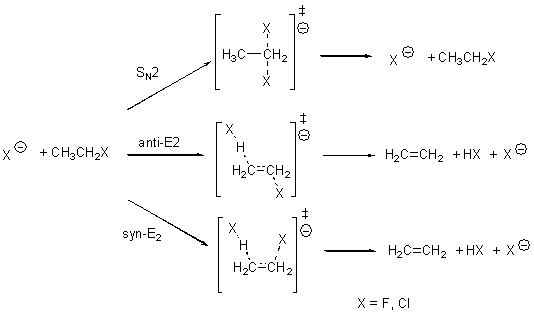
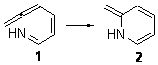
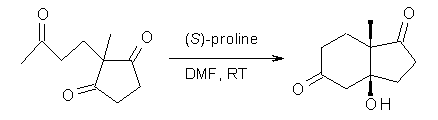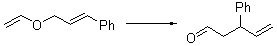What is the rate determining step in the Hajos-Parrish-Eder-Sauer-Wiechert reaction (reaction 1)? This basic question of the mechanism for the first example of the use of proline as a catalyst remains unanswered, though a recent paper by Meyer and Houk1 does moves us forward.
|
|
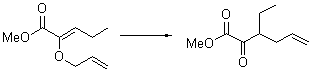
Reaction 1 |
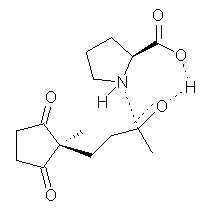
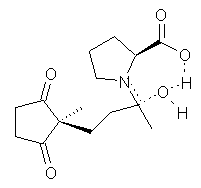
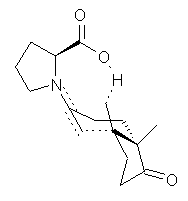
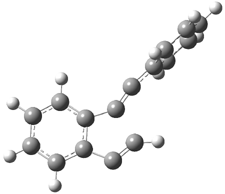
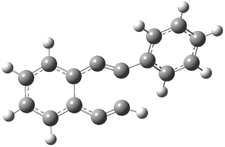
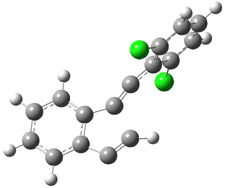
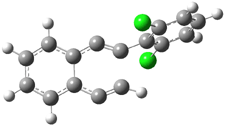
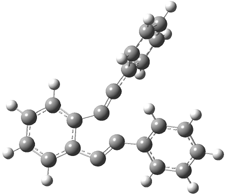
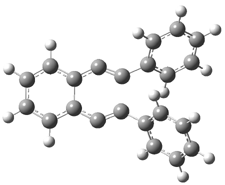
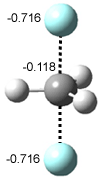
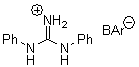
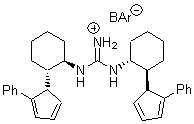
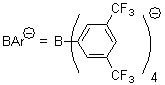
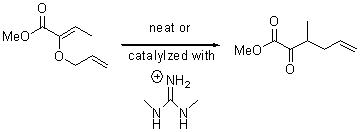
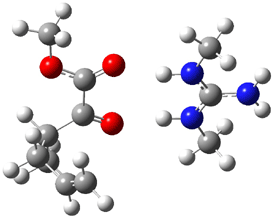
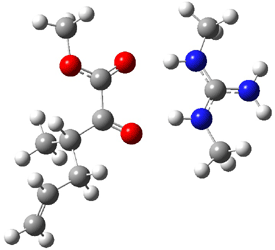
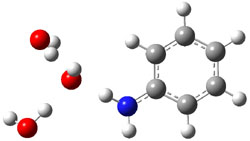
Their 13C kinetic isotope effect study revealed that only the nucleophilic ketone (the carboyl of the butyl chain) experiences any significant effect, with a value of about 1.03. B3LYP/6-31G(d,p) computations of the three transition states shown below were performed for both the gas phase and solution using IEF-PCM. Calculations of the transition state for the formation of the C-C bond (TS3) predicts no kinetic isotope effect, indicating that it is not the rate limiting step, in conflict with previous2 suggestions. The transition states for the formation of the carbinolamine (TS1) and formation of the iminium (TS2) both predict an isotope effect comparable with experiment. TS1 is about 3 kcal mol-1 higher in energy than TS2. The authors conclude that a step prior to formation of the C-C is the rate limiting step of the Hajos-Parrish-Eder-Sauer-Wiechert reaction, but cannot discern between the two possibilities examined.
|
|
|
|
|
TS1 |
TS2 |
TS3 |
References
(1) Zhu, H.; Clemente, F. R.; Houk, K. N.; Meyer, M. P., "Rate Limiting Step Precedes C-C Bond Formation in the Archetypical Proline-Catalyzed Intramolecular Aldol Reaction," J. Am. Chem. Soc., 2009, 131, 1632-1633, DOI: 10.1021/ja806672y.
(2) Clemente, F. R.; Houk, K. N., "Computational Evidence for the Enamine
Mechanism of Intramolecular Aldol Reactions Catalyzed by Proline," Angew. Chem. Int. Ed., 2004, 43, 5766-5768, DOI: 10.1002/anie.200460916.
InChIs
2-methyl-2-(3-oxobutyl)cyclopentane-1,3-dione:
InChI=1/C10H14O3/c1-7(11)5-6-10(2)8(12)3-4-9(10)13/h3-6H2,1-2H3
InChIKey=OZBYSCPBJGAYMQ-UHFFFAOYAW
(3aS,7aS)-3a-hydroxy-7a-methyl-3,4,6,7-tetrahydro-2H-indene-1,5-dione:
InChI=1/C10H14O3/c1-9-4-2-7(11)6-10(9,13)5-3-8(9)12/h13H,2-6H2,1H3/t9-,10+/m1/s1
InChIKey=PUHCDQVSBDIJTM-ZJUUUORDBA