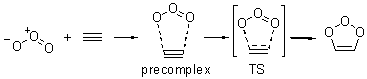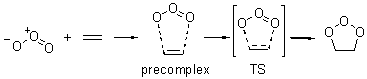The composite methods (exemplified by the Gaussian-n methods, the Weizmann-n methods and CNS-Q methods) are popularly held to be perhaps the best (if not the most straightforward and mechanical) procedures for obtaining accurate energetics. Errors are generally thought to be in the 1-2 kcal mol^-1 range – quite suitable for comparisons with experiment. The recent study of the 1,3-dipolar cycloaddition of ozone with ethene or ethyne offers serious food for thought about considering these composite methods as simple “black-box” solutions towards obtaining good results.
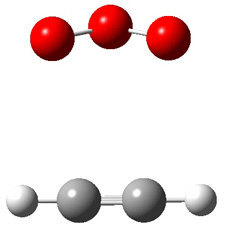
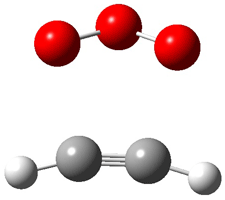
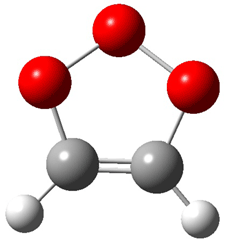
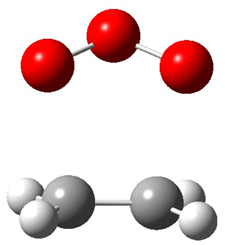
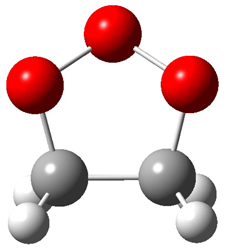
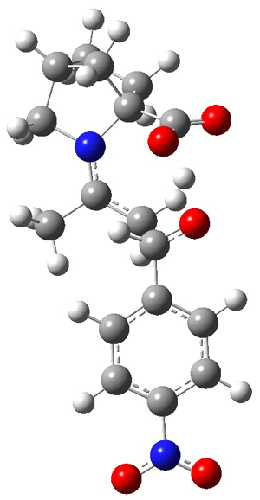
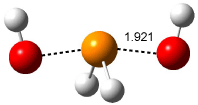
Wheeler, Ess, and Houk have examined the cycloaddition of ozone with ethyne (Reaction 1) and ethane (Reaction 2) with a variety of different computational techniques.¹ Shown in Figure 1 are the CCSD(T)/cc-pVTZ optimized geometries of the pre-complex, transition state and product for both reactions. One of the potential challenges of these reactions is that ozone has appreciable radical character which is also likely to be true in the pre-complex and transition state but the product should have little to no radical character.

Reaction 1
Precomplex	TS	Product
Reaction 2
Precomplex	TS	Product

The relative enthalphies (0K) of the complex, TS and product were computed using a number of different composite methods. The CBS-QB3, G3, G3B3, G3MP2B3 and G4^2,3 results are listed in Table 1 for both reactions. All of these methods claim a small error – perhaps 1-2 kcal mol^-1. The Gaussian-n methods nicely cluster for the reaction energy for both reactions, while CBS-QB3 predicts both reactions are more exothermic. (The same is also true of CBS-APNO.) The G-n methods indicate that the precomplex is essentially unbound. More concerning is the spread in the enthalpy values of the reaction barrier: the G-n methods predict a barrier that ranges over 5 kcal mol^-1.

Table 1. Relative enthalpies (kcal mol^-1) of the critical points for Reactions 1 and 2.¹

So what is the correct barrier height? A focal point extrapolation procedure was then performed. This seeks to extrapolate to infinite basis set and estimate the effects of correlation through CCSDT(Q) and includes corrections for the Born-Oppenheimer approximation and special relativistic effects. The focal point results are also shown in Table 1. The new G4 composite method gives enthalpies in very nice agreement with those obtained with the much more expensive focal point procedure. However, the other composite methods fair much worse, especially for the activation barrier.
The convergence of the focal point method for the reaction energy is slow, leading to a large error bar of 2 kcal mol^-1. This appears to relate to the radical character difference between the reactant and product. The convergence for the activation barrier is much better (an error of only 0.2 kcal mol^-1) and here the comparison is between reactant and TS which have similar radical character.
Perhaps the most discouraging aspect of this study is that the relative energy predicted using the highest computational component of the composite method – so, CCSD(T)/6-31+G* for the CBS-QB3 method and QCISD(T)/6-31G(d) for the G3 methods – are more accurate than the composite method itself. But, the reasonable performance of the new G4 method^2,3 does offer some glimmer of hope here.

References

(1) Wheeler, S. E.; Ess, D. H.; Houk, K. N., "Thinking
Out of the Black Box: Accurate Barrier Heights of 1,3-Dipolar Cycloadditions of Ozone with Acetylene and Ethylene," J. Phys. Chem. A, 2008, 112, 1798-1807, DOI: 10.1021/jp710104d.

(2) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory," J. Chem. Phys., 2007, 126, 084108, DOI: 10.1063/1.2436888

(3) Curtiss, L. A.; Redfern, P. C.; Raghavachari, K., "Gaussian-4 theory using
reduced order perturbation theory," J. Chem. Phys., 2007, 127, 124105-8, DOI: 10.1063/1.2770701.

InChIs

Reaction 1 product: InChI=1/C2H2O3/c1-2-4-5-3-1/h1-2H

Reaction 2 product: InChI=1/C2H4O3/c1-2-4-5-3-1/h1-2H2

Birney has published another study of a pseudopericyclic reaction to complement the many I discus in Chapter 3.4. Here he looks at that decarbonylation of benzothiophenedione 1, which if analogous to the furandione will first give the ketene 2 before forming 3.¹ Upon gentle heating, 3 dimerizes to 4. Interestingly, 2 has not been detected.²

2 does not exist as a local minimum on the B3LYP/6-31G(d,p) or G3MP2B3 surfaces; rather all optimizations collapse to 3. However, when optimized with PCM with the dielectric of DMSO, 2 is a local minimum.

The transition state for loss of CO from 1 leads directly to 3. This TS (TS1-3, see Figure 1) is non-planar, unlike for the analogous reaction of the furandione. TS1-3 does not correspond with a pseudopericyclic reaction.

TS1-3

TS3-4

Figure 1. B3LYP/6-31G(d,p) optimized geometries of TS1-3 andTS3-4.¹

The transition state for the dimerization of 3 (TS3-4), also shown in Figure 1, appears to be a [2σs + σs] cyclization, which is thermally forbidden. However, analysis of the molecular orbitals indicates the interaction of sets of orthogonal orbitals, exemplary of a pseudopericyclic reaction. The barrier for this reaction, 17.9 kcal mol^-1, is consistent with an allowed pseudopericyclic process.

References

(1) Sadasivam, D. V.; Birney, D. M., "A Computational Study of the Formation and Dimerization of Benzothiet-2-one," Org. Lett., 2008, 10, 245-248, DOI: 10.1021/ol702628v.

(2) Wentrup, C.; Bender, H.; Gross, G., "Benzothiet-2-ones: Synthesis, Reactions, and Comparison with Benzoxet-2-ones and Benzazetin-2-ones," J. Org. Chem., 1987, 52, 3838-3847, DOI: 10.1021/jo00226a022.

InChIs

1: InChI=1/C8H4O2S/c9-7-5-3-1-2-4-6(5)11-8(7)10/h1-4H

2: InChI=1/C7H4OS/c8-5-6-3-1-2-4-7(6)9/h1-4H

3: InChI=1/C7H4OS/c8-7-5-3-1-2-4-6(5)9-7/h1-4H

4: InChI=1/C14H8O2S2/c15-13-9-5-1-3-7-11(9)17-14(16)10-6-2-4-8-12(10)18-13/h1-8H

I guess one can never know enough about the S_N2 reaction! Wester and co-workers have performed careful crossed molecular beam imagining on the reaction Cl^– + CH₃I.¹ In collaboration with Hase, they have employed MP2/ECP/aug-cc-pVDZ computations to get the potential energy surface for the reaction and direct molecular dynamics. The PES is exactly as one would expect for a gas phase ion-molecule reaction: the transition state has backside attack of the nucleophile and it connects to two ion-dipole complexes (see Chapter 5.1.1).

The experiments are interpreted with the help of the MD computations. At low energy one sees formation of the complex. At higher energies, the direct backside attack reaction occurs. And at higher energies a new reaction path emerges, as sketched out in Figure 1. As the nucleophile (chloride) approaches methyl iodide, the methyl group rotates towards the nucleophile. The methyl group then collides with the nucleophile, which sends the methyl group spinning about the iodine atom in the opposite direction. The methyl group rotates all the way around the iodine atom and when it approaches the chloride a second time, the displacement reaction occurs and product is formed. They term this process a “roundabout mechanism”, and they have some experimental evidence for the occurrence of the double roundabout (two rotations of the methyl group about the iodine)! I think we should anticipate seeing more and more interesting reaction pathways as experimental and theoretical techniques continue to allow us a more detailed and precise view of motion of individual molecules across barriers.

Figure 1. Schematic of the trajectory illustrating the roundabout mechanism.
Chlorine is yellow, iodine is pink and carbon is black.

References

(1) Mikosch, J.; Trippel, S.; Eichhorn, C.; Otto, R.; Lourderaj, U.; Zhang, J. X.; Hase, W. L.; Weidemüller, M.; Wester, R., "Imaging Nucleophilic Substitution Dynamics," Science 2008, 319, 183-186, DOI: 10.1126/science.1150238.

In Chapter 5.3.2, I extensively discuss the organocatalyzed aldol reaction. Barbas and List have pioneered the use of proline to catalyze this reaction, and Houk has performed a series of computational studies to discern the mechanism. The mechanism is essentially the attack of the enamine on the carbonyl with concomitant proton transfer from the carboxylic acid to the forming oxyanion.

Shininisha and Sunoj have examined a number of bicyclic analogues of proline (1-11) as catalysts of the aldol reaction.¹ They computed the activation energies for the reaction of the enamine derived from acetone with p-nitrobenzaldehyde with the various catalysts. All computations were performed at B3LYP/6-311+G**//B3LYP/6-31G* with the solvent effects modeled using CPCM.

As Houk has demonstrated, there are four possible transition states: the attack can come to either the re or si face of the aldehyde and either the syn or anti enamine can be the reactant. The four transition states for the reaction of 8 are shown in Figure 1. These TSs are representative of all of the transition states involving the different catalysts, including proline itself. These TS are characterized by proton transfer accompanying the C-C bond formation. Their relative energies can be interpreted in terms of the distortions about the enamine double bond (the more planar, the lower the energy) and the arrangement of the carboxylic acid and the incipient oxyanion. These arguments were made by Houk and are described in my book.

8-anti-re 0.0	8-anti-si 2.12
8-syn-re 8.15	8-syn-si 7.28

Figure 1. B3LYP/6-311+G**//B3LYP/6-31G* optimized structures and relative energies (kcal/mol) of the transition states of the enamine derived from acetone and 8 with p-nitrobenzaldehyde¹

The enantiomeric excess predicted by the computations for the aldol reaction using the 11 different bicyclic catalysts is presented in Table 1. All of the catalysts except 11 give high enantiomeric excess, with a number of them predicted to produce an ee above 90%. The authors conclude that these catalysts are worth exploring, since they are predicted to perform better than proline (which has a predicted ee of 75%).

Table 1. Predicted ee for the reaction of the enamine derived
from acetone and catalyst with p-nitrobenzaldehyde.

References

(1) Shinisha, C. B.; Sunoj, R. B., "Bicyclic Proline Analogues as Organocatalysts for Stereoselective Aldol Reactions: an in silico DFT Study," Org. Biomol. Chem., 2007, 5, 1287-1294, DOI: 10.1039/b701688c.

InChIs

1: InChI=1/C8H13NO2/c1-5-4-6-2-3-8(5,9-6)7(10)11/h5-6,9H,2-4H2,1H3,(H,10,11)

2: InChI=1/C8H13NO2/c1-5-4-8(7(10)11)3-2-6(5)9-8/h5-6,9H,2-4H2,1H3,(H,10,11)

3: InChI=1/C6H9NO2/c8-5(9)6-2-1-4(3-6)7-6/h4,7H,1-3H2,(H,8,9)

4: InChI=1/C6H9NO3/c8-5(9)6-2-1-4(7-6)10-3-6/h4

5: InChI=1/C5H7NO3/c7-4(8)5-1-3(6-5)9-2-5/h3,6H,1-2H2,(H,7,8)

6: InChI=1/C6H9NO2S/c8-5(9)6-2-1-4(7-6)10-3-6/h4,7H,1-3H2,(H,8,9)

7: InChI=1/C5H7NO2S/c7-4(8)5-1-3(6-5)9-2-5/h3,6H,1-2H2,(H,7,8)

8: InChI=1/C7H11NO2/c9-6(10)7-2-1-5(3-7)4-8-7/h5,8H,1-4H2,(H,9,10)

9: InChI=1/C7H11NO2/c9-7(10)6-4-1-2-5(3-4)8-6/h4-6,8H,1-3H2,(H,9,10)

10: InChI=1/C6H9NO2/c8-6(9)5-3-1-4(2-3)7-5/h3-5,7H,1-2H2,(H,8,9)

11: InChI=1/C6H9NO2/c8-6(9)5-3-1-4(5)7-2-3/h3-5,7H,1-2H2,(H,8,9)

In Chapter 7.3.5.1 I discuss the computational and experimental results of Singleton¹ regarding C₂-C₆ enyne allene cyclization. The reaction is shown below, and though Singleton could locate no transition state that connects the reactant to the diradical, molecular dynamics trajectory calculations show that the diradical is sampled, though the dominant pathway is the concerted route.

Schmittel has expanded on this work by determining the kinetic isotope effects for four more analogues.2 The results are summarized in Table 1. Depending on the substituent, the predominant pathway can be concerted or stepwise or even a mixture of these two (termed “boundary”). Schmittel argues that the region about the single transition state, the one that directly connect reactant to product through a concerted path, is actually quite flat. This is a “broad transition state zone”. Trajectories can traverse through various regions of the zone, some that go on to diradical, some that go on to product. Substituents can alter the shape of the TS zone and thereby shift the set of trajectories in one direction or the other. The upshot is further support for the importance on non-statistical dynamics in dictating the course of reactions.

Table 1. Kinetic isotope effects for C₂-C₆ enyne allene cyclizations

References

(1) Bekele, T.; Christian, C. F.; Lipton, M. A.; Singleton, D. A., ""Concerted" Transition State, Stepwise Mechanism. Dynamics Effects in C²-C⁶ Enyne Allene Cyclizations," J. Am. Chem. Soc. 2005, 127, 9216-9223, DOI: 10.1021/ja0508673.

(2) Schmittel, M.; Vavilala, C.; Jaquet, R., "Elucidation of Nonstatistical Dynamic Effects
in the Cyclization of Enyne Allenes by Means of Kinetic Isotope Effects," Angew. Chem. Int. Ed. 2007, 46, 6911-6914, DOI: 10.1002/anie.200700709

In their continuing efforts to build novel aromatic systems, Siegel and Baldridge report the preparation of the decapropyl analogue of the per-ethynylated corrannulene 1.¹ They were hoping that this might cyclize to the bowl 2. It is however stable up to 100 °C, however, the analogue 3 was obtained in the initial preparation of decapropyl-1.

The B3LYP/cc-pVDZ optimized structures of 1 and 3 are shown in Figure 1. 1 is bowl-shaped, reflecting the property of corranulene, but interestingly 3 is planar. The geometry of the {10]annulene is interesting as it is more consistent with the alkynyl resonance form B.

1

3

Figure 1. B3LYP/cc-pVDZ optimized structures of 1 and 3.¹

Siegel and Baldridge speculate that the conversion of 1 → 3 occurs by first undergoing the Bergman cyclization to give 4, which then opens to give 3. Unfortunately, they did not compute the activation barrier for this process. They do suggest that further cyclization to give the hoped for 2 might be precluded by the long distances between radical center and neighboring alkynes in 4, but the radicals are too protected to allowing trapping by the solvent, allowing for the formation of 3.

References

(1) Hayama, T.; Wu, Y. T.; Linden, A.; Baldridge, K. K.; Siegel, J. S., "Synthesis, Structure, and Isomerization of Decapentynylcorannulene: Enediyne Cyclization/Interconversion of C₄₀R₁₀ Isomers," J. Am. Chem. Soc., 2007, 129, 12612-12613 DOI: 10.1021/ja074403b.

InChIs

1: InChI=1/C40H10/c1-11-21-22(12-2)32-25(15-5)26(16-6)34-29(19-9)30(20-10)35-28(18-8)27(17-7)33-24(14-4)23(13-3)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

2: InChI=1/C40H10/c1-2-12-14-5-6-16-18-9-10-20-19-8-7-17-15-4-3-13-11(1)21-22(12)32-24(14)26(16)34-29(18)30(20)35-28(19)27(17)33-25(15)23(13)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

3: InChI=1/C40H12/c1-9-23-25(11-3)33-27(13-5)29(15-7)35-30(16-8)28(14-6)34-26(12-4)24(10-2)32-22-20-18-17-19-21-31(23)36-37(32)39(34)40(35)38(33)36/h1-8,17-18,31-32H/b18-17-

Despite the fact that Wes Borden has indicated the he has written his last paper on the Cope rearrangement (see my interview with Wes at the end of Chapter 3), others remain intrigued by this reaction and continue to report on it. In a recent JACS communication, Tantillo¹ examines the palladium-promoted Cope rearrangement.

The ordinary Cope rearrangement displays chameleonic character – switching from concerted to stepwise with a diradical intermediate – based on substituents. The palladium-promoted Cope is suggested to proceed through a stepwise mechanism with a zwitterionic intermediate (Scheme 1).²

Scheme 1.

Tantillo¹ has examined a variety of these rearrangements at the B3LYP/LANL2DZ level. The palladium complex is PdCl₂NCMe. For all cases where R is a substituted phenyl group, the mechanism is stepwise, with the intermediate 1 sitting in a shallow well. The most stable intermediate (based on lying in the deepest well) is with the 4-dimethylaminophenyl group, and the well is 5.1 kcal mol^-1 deep. The structures of the transition state (2-pNMe₂) and the intermediate (1-pNMe₂) are shown in Figure 1.

2-pNMe2

1-pNMe2

Figure 1. B3LYP/LANL2DZ optimized structures of 2-pNMe₂ and 1-pNMe₂.¹

However, the well associated with 1 can be very shallow, as little as 0.4 kcal mol^-1 (R = 4-trifluoroimethylphenyl and 4-nitrophenyl). This suggests that perhaps when properly substituted the intermediate might vanish and the reaction become concerted. This is in fact what happens when R is CF₃, CN, or H. The transition state for the reaction with R = H is shown in Figure 2. So, this metal-assisted Cope rearrangement displays chameleonic behavior, just like the metal-free case, except that the intermediate is zwitterionic with the metal, instead of diradical in the metal-free cases.

2-H

Figure 1. B3LYP/LANL2DZ optimized structure of 2-H.¹

References

(1) Siebert, M. R.; Tantillo, D. J., "Transition-State Complexation in Palladium-Promoted [3,3] Sigmatropic Shifts," J. Am. Chem. Soc. 2007, 129, 8686-8687, DOI: 10.1021/ja072159i.

(2) Overman, L. E.; Renaldo, A. E., "Catalyzed Sigmatropic Rearrangements. 10. Mechanism of the Palladium Dichloride Catalyzed Cope Rearrangement of Acyclic Dienes. A Substituent Effect Study," J. Am. Chem. Soc. 1990, 112, 3945-3949, DOI: 10.1021/ja00166a034.

Jorgensen reports an enhanced QM/MM and ab initio study of the rate enhancement of Diels-Alder reactions in various solvents.¹ This study extends earlier studies that he and others have done, many of which are discussed in Chapter 6.2 of the book. In this study, he reports QM/MM computations using the PDDG/PM3 method for the QM component, and MP2 computations incorporating CPCM to account for bulk solvent effects.

The major advance in methodology in this paper is performing a two-dimensional potential of mean force analysis where these two dimensions correspond to the forming C-C distances. In addition, computations were done for water, methanol, acetonitrile and hexane as solvents. Highlights of the results are listed in Table 1.

Table 1. Computed bond asynchronicity^a and activation energy^b (kcal/mol) for the Diels-Alder reaction with cyclopentadiene.

The semi-empirical method underestimates the asynchronicity of these gas-phase Diels-Alder TSs. However, with inclusion of the solvent, the computations do indicate a growing asynchronicity with solvent polarity, This is associated with the ability of the solvent, especially protic solvents, to preferentially hydrogen bond to the carbonyl in the TS.

In terms of energetics, in must first be pointed out that the computations dramatically overestimate the activation barriers. However, the relative trends are reproduced: the barrier increases from water to methanol to acetonitrile to hexane. Jorgensen also computed the activation barriers at MP2/6-311+G(2d,p) with CPCM using the CBS=QB3 gas phase geometries. Some of these results are listed in Table 2. The results for water are in outstanding agreement with experiment. However, the results for the other solvents are poor, underestimating the increase in barrier in moving to the more polar solvent.

Table 2. MP2/6-311+G(2d,p)/CPCM values for ΔG^‡ (kcal/mol).

Bottom line, the conclusions of this study are in agreement with the earlier studies, namely that the hydrophobic effect (better may be the enforced hydrophobic interaction) and greater hydrogen bonding in the TS (both more and stronger hydrogen bonds) account for the rate acceleration of the Diels-Alder reaction in water.

References

(1) Acevedo, O.; Jorgensen, W. L., "Understanding Rate Accelerations for Diels-Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theory Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.

Just a short update here. In Chapter 5.1.2 we discuss nucleophilic substitution at heteroatoms. Unlike the paradigmatic case for substitution at carbon, which proceeds via the S_N2 mechanism. Nucleophilic substitution at second-row atoms (S, Si, P) appears to follow an addition-elimination pathway. Bickelhaupt¹ now adds a more thorough computational examination of nucleophilic substitution at phosphorus. He looked at a few identity reactions involving tricoordinate P, namely

X^– + PH₂X → PH₂X + X^–

X^– + PF₂X → PF₂X + X^–

X^– + PCl₂X → PCl₂X + X^–

where X is chloride or hydroxide. In all cases the only critical point located on the potential energy surface is for a tetracoordinate intermediate. Shown in Figure 1 are the intermediates for the reaction OH^– + PH₂OH and Cl^– + PCl₃. This result is consistent with the studies of nucleophilic substitution at sulfur and silicon.

(a) xyz file

(b) xyz file

Figure 1. OLYP/TZ2P optimized intermediate for the reaction (a) OH^– + PH₂OH
and (b) Cl^– + PCl₃.

References:

(1) vanBochove, M. A.; Swart, M.; Bickelhaupt, F. M., "Nucleophilic Substitution at Phosphorus (S_N2@P): Disappearance and Reappearance of Reaction Barriers," J. Am. Chem. Soc. 2006, 128, 10738-10744, DOI: 10.1021/ja0606529

The search for unusual potential energy surface topologies continues. Unusual surfaces can lead to dynamic effects that result in rates and product distributions dramatically divergent from that predicted by statistical theories. I addressed this topic in Chapter 7 of the book.

Houk has found another interesting example in the Diels-Alder reaction of cyclopentadiene with nitrostyrene 1.¹ The [4+2] adduct is 2, which can undergo a [3,3] Cope-like rearrangement to give 3. Product 3 can also result from a [2+4] Diels-Alder cycloaddition where cyclopentadiene acts as the dienophile.

Like some of the examples in Chapter 7, the potential energy surface, computed at B3LYP/6-31+G*, contains a single transition state (TS1) from reactants. Continuing on the reaction path past the transition state, a valley ridge inflection point (VRI) intervenes, causing the path to bifurcate: one path leads to 2 and the other leads to 3. In other words, a single transition state leads to two different products! TS1 is geometrically closer to 2 than 3, while TS2 lies closer to 3 than 2 (Figure 1). This topology directs most molecules to traverse a path over TS1 and on to 2. What is novel in this paper is that the acid-catalyzed reaction, using SnCl₄, shifts TS1 towards 3 and TS2 towards 2, leading to the opposite product distribution. The uncatalyzed reaction favors formation of 2 while the catalyzed reaction favors 3 over 2. Confirmation of this prediction awaits a molecular dynamics study.

TS1	TS1-Cat
TS2	TS2-Cat

Figure 1. B3LYP/6-31+G(d) optimized structures for TS1 and TS2.¹

References

(1) Celebi-Olcum, N.; Ess, D. H.; Aviyente, V.; Houk, K. N., “Lewis Acid Catalysis Alters the Shapes and Products of Bis-Pericyclic Diels-Alder Transition States,” J. Am. Chem. Soc., 2007, 129, 4528-4529. DOI: 10.1021/ja070686w

InChI

1: InChI=1/C8H7NO2/c10-9(11)7-6-8-4-2-1-3-5-8/h1-7H/b7-6+
2: InChI=1/C13H13NO2/c15-14(16)13-11-7-6-10(8-11)12(13)9-4-2-1-3-5-9/h1-7,10-13H,8H2
3: InChI=1/C13H13NO2/c15-14-9-12(10-5-2-1-3-6-10)11-7-4-8-13(11)16-14/h1-6,8-9,11-13H,7H2