I did not present π-π stacking in the book, but I think if I ever do a second edition, I will include a discussion of it. I’m not sure quite where it would fit in given the current structure of the book (I discuss DNA bases and base pairs in the context of solvation in Chapter 6), but the paper I will discuss next gives me some idea – π-π stacking is a sensitive test of the quality of computational methods and this could be part of Chapter 1 as a discussion of the failings of methods, especially DFT.
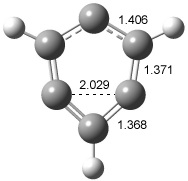
Swart and Bickelhaupt have examined a series of π-π stacked pairs, evaluating them regarding how DFT performs.1 Their first example is the benzene dimer (Table 1). At CCSD(T) the dimer binding energy is 1.7 kcal mol-1 and the rings are 3.9 Å apart. LDA, KT1 (yet another newly minted functional2,3), and BHandH get the separation and binding energy reasonably well. PW91 gets the distance too big and underestimates the binding energy. But most important is that the other (more traditional) functionals indicate that the PES is entirely repulsive! This is a manifestation of many functionals’ inability to properly account for dispersion.
Table 1. Optimized separation distance (rmin, Å) and binding energy (kcal mol-1)
of the benzene dimer using the TZ2P basis set.1
|
|
||
|
Method |
rmin |
ΔE |
|
CCSD(T) |
3.9 |
-1.70 |
|
LDA |
3.8 |
-1.33 |
|
KT1 |
3.8 |
-1.58 |
|
BHandH |
3.9 |
-0.89 |
|
PW91 |
5.0 |
-0.45 |
|
BLYP |
repulsive |
|
|
BP86 |
repulsive |
|
|
OLYP |
repulsive |
|
|
B3LYP |
repulsive |
|
|
|
||
Next, they compare 14 different orientations of stacked dimmers of cytosine. The energies of these dimmers were computed using again a variety of functionals and compared to MP2/CBS energies with a correction for CCSD(T). The mean absolute deviations (MAD) for the energies using the various functionals are listed in Table 2. Again, LDA and KT1 perform quite well, but most functionals do quite poorly.
Table 2. Mean absolute deviations of the energies of 14 cytosine
stacked dimer structures compared to their MP2 energies.
|
|
||
|
Method |
MAD |
|
|
LDA |
0.38 |
|
|
KT1 |
0.47 |
|
|
BHandH |
0.52 |
|
|
PW91 |
6.04 |
|
|
BLYP |
9.52 |
|
|
BP86 |
8.75 |
|
|
OLYP |
14.80 |
|
|
B3LYP |
8.24 |
|
|
|
||
Similar results are also demonstrated for stacked DNA bases and also stacked base pairs. These authors conclude that the KT1 functional appears suitable for treating π-π stacking. One should also consider some of the new functionals from the Truhlar group,4-6 which unfortunately are not included in this study.
References
(1) Swart, M.; van der Wijst, T.; Fonseca, C.; Bickelhaput, F. M., "π-π Stacking Tackled with Density Functional Theory," J. Mol. Model. 2007, 13, 1245-1257, DOI: 10.1007/s00894-007-0239-y.
(2) Keal, T. W.; Tozer, D. J., "The Exchange-Correlation Potential in Kohn–Sham Nuclear Magnetic Resonance Shielding Calculations," J. Chem. Phys. 2003, 119, 3015-3024, DOI: 10.1063/1.1590634
(3) Keal, T. W.; Tozer, D. J., "A Semiempirical Generalized Gradient Approximation Exchange-Correlation Functional," J. Chem. Phys. 2004, 121, 5654-5660, DOI: 10.1063/1.1784777.
(4) Zhao, Y.; Truhlar, D. G., "A Density Functional That Accounts for Medium-Range Correlation Energies in Organic Chemistry," Org. Lett. 2006, 8, 5753-5755, DOI: 10.1021/ol062318n
(5) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., "Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions," J. Chem. Theory Comput., 2006, 2, 364-382, DOI: 10.1021/ct0502763.
(6) Zhao, Y.; Truhlar, D. G., "Assessment of Model Chemistries for Noncovalent Interactions," J. Chem. Theory Comput. 2006, 2, 1009-1018, DOI: 10.1021/ct060044j