Somehow I missed this paper when it came out a few months ago, even though I was aware it was coming – as I mentioned it in one of my previous posts!

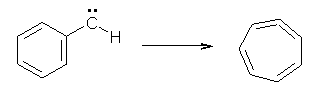
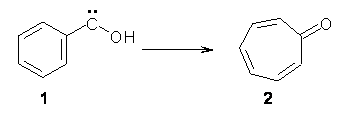
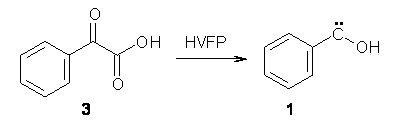
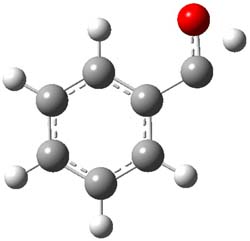
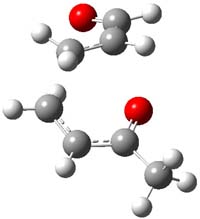
Anyways, Schreiner and Allen reported on their third study of hydroxyl carbenes (see these posts on dihydroxymethylene and hydroxymethylene), this time examining phenylhydroxycarbene.¹ As I covered in my book, there is a lot of work on phenylcarbenes which typically ring expand to the cycloheptatetraene, see Reaction 1. One might expect phenylhydroxycarbene to do the same thing, i.e. 1 converting into 2 (Reaction 2). 1 is prepared by high-vacuum flash pyrolysis of phenylglyoxylic acid 3 and then capturing the product in an argon matrix at 11 K (Reaction 3).

The carbene 1 is identified through comparison of its experimental and computed (anharmonic frequencies at CCSD(T)/cc-pVDZ) IR frequencies.

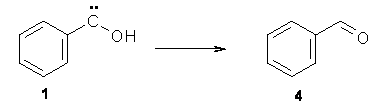
No ring expansion is observed at all – Reaction 2 does not occur. Instead, 1 rearranges to benzaldehyde 4 (Reaction 4) at 11 K with a half life of 2.46 h (and a half life of 2.55 h at 20 K). The deuterated analogue does not convert to benzaldehyde and 1-d appears to be completely stable.

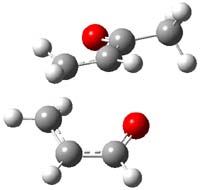
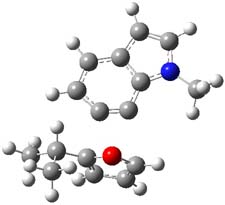
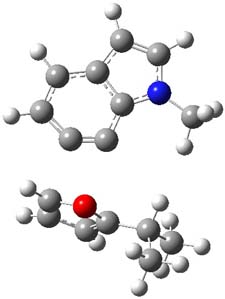
So, what is going on? The cis and trans forms of 1 interconvert through a barrier of 22.7 kcal mol^-1. The trans isomer can convert to benzaldehyde (the reaction is very exothermic: -50.8 kcal mol^-1) with a barrier of 28.8 kcal mol^-1 through TS1, shown in Figure 1. The cis isomer can cleave into benzene and CO (not observed) with a huge barrier of 55 kcal mol^-1. All of these barrier were computed at CCSD(T)/cc-pVQZ.

TS1

Figure 1. MP2/cc-pVDZ optimized transition state for the conversion of 1 into 4.

Benzaldehyde seems to be produced by passing through a huge barrier, something that is impossible from a thermal perspective (we’re at 11 K!). But this can be accomplished by tunneling. Tunneling probabilities were computed from the MP2/aug-cc-pVDZ intrinsic reaction path with barrier penetration integrals computed with the WKB approximation. The bottom line: the computed half-life is 3.3 h and the deuterated species is computed to have a half-life of 8700 years(!), both in excellent agreement with experimental observation. Quantum mechanical tunneling is clearly the explanation for this chemistry.

This is another fine example of the power of joint experimental/computational studies. And be on the look-out for an even more exciting case from this group. I met with Wes Allen on my recent trip to the University of Georgia and was entertained with another hydroxycarbene that undergoes quite novel tunneling!

References

(1) Gerbig, D.; Reisenauer, H. P.; Wu, C.-H.; Ley, D.; Allen, W. D.; Schreiner, P. R., "Phenylhydroxycarbene," J. Am. Chem. Soc., 2010, 132, 7273-7275, DOI: 10.1021/ja9107885

InChIs

1: InChI=1/C7H6O/c8-6-7-4-2-1-3-5-7/h1-5,8H
InChIKey=QVZIGMRPQWIGCV-UHFFFAOYAE

2: InChI=1/C7H6O/c8-7-5-3-1-2-4-6-7/h1-6H
InChIKey=QVWDCTQRORVHHT-UHFFFAOYAM

3: InChI=1/C8H6O3/c9-7(8(10)11)6-4-2-1-3-5-6/h1-5H,(H,10,11)/f/h10H
InChIKey=FAQJJMHZNSSFSM-KZFATGLACS

4: InChI=1/C7H6O/c8-6-7-4-2-1-3-5-7/h1-6H
InChIKey=HUMNYLRZRPPJDN-UHFFFAOYAE

The de novo design of catalysts for specific purposes remains an inspired goal for chemists and biochemists. Ken Houk and David Baker have been pursuing this goal, and their recent paper on the design of a catalyst for the bimolecular Diels-Alder¹ is a real significant step forward.

Their model enzyme is one that will provide a hydrogen bond acceptor to the carbamate proton of 1 and a proton donor to the carbonyl oxygen of the amide 2. This model is sketched in Figure 1. Glutamine or asparagines will serve as the acceptor and serine, threonine, or tyrosine will serve as the proton donor. The catalytic site is then modeled, and then this active site is fit within 207 protein scaffolds. About 10¹⁹ active site configurations are reduced to about 10⁶ possible protein scaffolds. Optimization of these led to 84 protein designs.

Figure 1. Enzyme model

These 84 possible proteins were then synthesized within E. coli and then tested for catalytic behavior
in the Diels-Alder reaction of 1 + 2. Only 2 enzymes have activity, and with some protein modifications, quite reasonable enzyme activity is found. These enzymes show strong selectivity for the substrates – addition of a methyl group significantly diminishes catalytic activity. Perhaps most important is that of the 8 possible isomers that can be formed (4 isomers are produced in the uncatalyzed reaction) only 1 is produced here, the 3R,4S isomer 3.

All-in-all, a quite remarkable accomplishment!

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D.,
"Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239.

InChIs

1: InChI=1/C13H13NO4/c1-2-3-8-14-13(17)18-9-10-4-6-11(7-5-10)12(15)16/h2-8H,1,9H2,(H,14,17)(H,15,16)/p-1/b8-3+/fC13H12NO4/h14H/q-1
InChIKey=HGMJQUSLRHRARW-OSXKDGDFDJ

2: InChI=1/C5H9NO/c1-4-5(7)6(2)3/h4H,1H2,2-3H3
InChIKey=YLGYACDQVQQZSW-UHFFFAOYAD

3: InChI=1/C18H22N2O5/c1-20(2)16(21)14-5-3-4-6-15(14)19-18(24)25-11-12-7-9-13(10-8-12)17(22)23/h4,6-10,14-15H,3,5,11H2,1-2H3,(H,19,24)(H,22,23)/p-1/t14-,15+/m0/s1/fC18H21N2O5/h19H/q-1
InChIKey=WWWDBAXWGWLFSD-AFFTYDCXDH

The α-proton of ketones and aldehydes are acidic, thanks to delocalization of the resulting anion. However, α-protons at a bridgehead position are much less acidic – the resulting anion is not delocalized as the enolate would be an anti-Bredt alkene. So, what about more remote protons from the carbonyl – would they exhibit enhanced acidity due to inductive or field effects?

Kass has examined the deprotonation of 2-adamantone 1 via experiment and computation.¹ The relative energies of the five different anions are listed in Table 1. Previous H/D exchange experiments indicate that the relative reactivity is β_ax > β_eq > α, and this is well reproduced by computations.²

Table 1. Relative energies (kcal mol^-1) of the enolates of 1.

Kass’ bracketing experiments indicate the enthalpy for deptrotonation of 2-adamantone is 394.7 ± 1.4 kcal mol^-1. This is in nice accord with the computational results for loss of the β_ax proton: 393.8 (M06-2x/aug-cc-pVDZ) and 396.8 kcla mol^-1 (G3). One interesting computational result is a competive cyclic structure 2, whose stability is similar to that to the β_ax ion at M06-2x and is the optimized structure produced at MP2/6-31G(d) when searching for the β_eq enolate.

So, to answer our question, protons remote from a carbonyl are more acidic than alkane
analogues, but much less acidic than typical α-protons of ketones.

References

(1) Meyer, M. M.; Kass, S. R., "Enolates in 3-D: An Experimental and Computational Study of Deprotonated 2-Adamantanone," J. Org. Chem., 2010, 75, 4274-4279, DOI: 10.1021/jo100953y

(2) Stothers, J. B.; Tan, C. T., "Adamantanone: stereochemistry of its homoenolization as shown by ²H nuclear magnetic resonance," J. Chem. Soc., Chem. Commun., 1974, 738-739, DOI: 10.1039/C39740000738

InChI

1: InChI=1/C10H14O/c11-10-8-2-6-1-7(4-8)5-9(10)3-6/h6-9H,1-5H2
InChIKey=IYKFYARMMIESOX-UHFFFAOYAE

2: InChI=1/C10H13O/c11-10-7-2-5-1-6(4-7)9(10)8(10)3-5/h5-9H,1-4H2/q-1
InChIKey=WTXOXRNASCZDME-UHFFFAOYAE

Often gem-dialkyl substitution accelerates a reaction, for example in the formation of an epoxide via reaction 1. Here the relative rates are 1:21:252 in going from 1 to 2 to 3.¹ This acceleration is the Thorpe-Ingold effect and had been suggested to arise from a steric reaction: that the methyl groups contract the angle and bring the terminal groups closer together.

1: R₁ = R₂ = H
2: R₁ = Me, R₂ = H
3: R₁ = R₂ = Me

Kostal and Jorgensen² have examined the reaction of the 2-chloroethoxides 1-3 using computations, especially to look at the effect of solvent. At MP2/6-311+G(d,p) and CBS-Q, the relative rates (based on the activation free energy ΔG^‡) are 1:2.8:17 and 1:0.7:3.7, respectively. Evidently there is no significant rate enhancement afforded by gem-substitution in the gas phase.

However, solution computations give a very different result. Using PCM along with the MP2 method, the computed relative rates are 1:5.8:1100 and with the Monte Carlo-Free Energy Perturbation method, the relative rates for aqueous solution are 1:30:773. Thus, the Thorpe-Ingold acceleration is due to solvent. Analysis of the hydrogen bonded structures and the solute-water pair distributions suggest that increasing alkyl substitution reduces the strength of solvation of the reactant, leading to the lower activation barrier.

References

(1) Jung, M. E.; Piizzi, G., "gem-Disubstituent Effect:Theoretical Basis and Synthetic Applications," Chem. Rev., 2005, 105, 1735-1766, DOI: 10.1021/cr940337h

(2) Kostal, J.; Jorgensen, W. L., "Thorpe-Ingold Acceleration of Oxirane Formation Is Mostly a Solvent Effect," J. Am. Chem. Soc., 2010, 132, 8766-8773, DOI: 10.1021/ja1023755

The chemical shift of the benzene proton is about 7.3ppm, significantly downfield from the range of olefinic protons (5.6-58.ppm). This is rationalized as the standard induced diatropic ring current, found in aromatic species. But what should we make of the chemical shift of the protons in cyclobutadiene at 5.8 ppm? Shouldn’t this be much further upfield?

Schleyer and Mo have applied the block localized wavefunction (BLW) technique to aromatic and antiaromatic chemical shifts.¹ In BLW, self-consistent localized orbitals are produced to describe a particular resonance structure. So, for benzene, BLW describes in effect 1,3,5-cyclohexatriene, lacking any resonance energy.  When chemical shifts are computed with the BLW description, the proton chemical shift is 6.6 ppm, and is even more upfield if the geometry is optimized (in D_3h symmetry) with the BLW method (δ=6.2ppm). Furthermore the NICS(0)_πzz (the tensor component corresponding to the perpendicular direction evaluated in the ring center using just the π orbitals) is -36.3 for benzene and 0.0 for the D_3h BLW variant, strongly indicating the role of cyclic delocalization in affecting chemical shifts.

Now for cyclobutadiene, the proton chemical shift of 5.7 ppm becomes 7.4 in the BLW case. NICS(0)_πzz for cyclobutadiene is +46.9 and +1.6 in the BLW case. The problem is that typical alkenes are poor references for cyclobutadiene – when resonance is turned off, the chemical shift does move downfield – indicating the expected upfield shift for cyclobutadiene. Schleyer and Mo suggest that 3,4-dimethylenecyclobutene is a more suitable reference; its ring protons have chemical shifts of 7.65ppm.

They also describe computations of benzocyclobutadiene and tricyclobutenabenzene and offer straightforward rationalizations of their aromatic vs. antiaromatic behavior.

References

(1) Steinmann, S. N.; Jana, D. F.; Wu, J. I.-C.; Schleyer, P. v. R.; Mo, Y.; Corminboeuf, C., "Direct Assessment of Electron Delocalization Using NMR Chemical Shifts," Angew. Chem. Int. Ed., 2009, 48, 9828-9833, DOI: 10.1002/anie.200905390

InChIs

benzene: InChI=1/C6H6/c1-2-4-6-5-3-1/h1-6H
InChIKey=UHOVQNZJYSORNB-UHFFFAOYAH

cyclobutadiene: InChI=1/C4H4/c1-2-4-3-1/h1-4H
InChIKey=HWEQKSVYKBUIIK-UHFFFAOYAI

3,4-dimethylenecyclobutene: InChI=1/C6H6/c1-5-3-4-6(5)2/h3-4H,1-2H2
InChIKey=WHCRVRGGFVUMOK-UHFFFAOYAP

Dynamic effects rear up yet again in a seemingly simple reaction. Singleton has examined the Diels-Alder cycloaddition of acrolein with methyl vinyl ketone to give two cross products 1 and 2.¹ Upon heating the product mixture, 1 is essentially the only observed species. The retro-Diels-Alder is much slower than the conversion of 2 into 1. Using a variety of rate data, the best estimate for the relative formation of 1:2 is 2.5.

The eight possible transition states for this reaction were computed with a variety of methodologies, all providing very similar results. The lowest energy TS is TS3. A TS of type TS4 could not be found; all attempts to optimize it collapsed to TS3.

IRC computations indicate the TS3 leads to 1. The lowest energy TS that leads to 2 is TS6, but a second TS (TS5) lower in energy than TS6 also leads to 1. The other TS are still higher in energy. A Cope-type TS that interconverts 1 and 2 (TS7) was also located. The geometries of these TSs are shown in Figure 1.

TS3 (0.0)	TS5 (4.2)
TS6 (5.2)	TS7 (-0.4)

Figure 1. MP2/6-311+G** optimized geometries and relative energies (kcal mol^-1) of TS3-TS7.¹

Ordinary transition state theory cannot explain the experimental results – the energy difference between the lowest barrier to 1 (TS3) and to 2 (TS6) suggests a rate preference of over 700:1 for 1:2. But the shape of the potential energy surface is reminiscent of others that have been discussed in both my book (Chapter 7) and this blog (see my posts on dynamics) – a surface where trajectories cross a single TS but then bifurcate into two product wells.

To address the chemical selectivity on a surface like this, one must resort to molecular dynamics and examine trajectories. In their MD study of the 296 trajectories that begin at TS3 with motion towards product, 89 end at 1 and 33 end at 2, an amazingly good reproduction of experimental results! Interestingly, 174 trajectories recross the transition state and head back towards reactants. These recrossing trajectories result from “bouncing off” the potential energy wall of the forming C₄-C₅ bond.

In previous work, selectivity in on these types of surfaces was argued in terms of which well the TS was closer to. But analysis of the trajectories in this case revealed that a strong correlation exists between the initial direction and velocity in the 98 cm^-1 vibration – the vibration that corresponds to the closing of the second σ bond, the one between C₆-O₁ (forming 1), in the negative direction, and closing the C­₃-O₈ bond (forming 2) in the positive direction. Singleton argues that this is a type of dynamic matching, and it might be more prevalent that previously recognized.

References

(1) Wang, Z.; Hirschi, J. S.; Singleton, D. A., "Recrossing and Dynamic Matching Effects on Selectivity in a Diels-Alder Reaction," Angew. Chem. Int. Ed., 2009, 48, 9156-9159, DOI: 10.1002/anie.200903293

InChIs

1: InChI=1/C7H10O2/c1-6(8)7-4-2-3-5-9-7/h3,5,7H,2,4H2,1H3
InChIKey=AOFHZPHBPUYLAG-UHFFFAOYAJ

2: InChI=1/C7H10O2/c1-6-3-2-4-7(5-8)9-6/h3,5,7H,2,4H2,1H3
InChIKey=PLZQHPPETMMEED-UHFFFAOYAD

Houk and Doubleday have a nice follow-up study¹ to their previous MD study² of 1,3-dipolar cycloadditions, which I posted on here. They report on the cycloaddition of either acetylene or ethylene to 9 different 1,3-dipoles. Continuing on Houk’s recent thread of looking at distortion energies to attain the TS, they note that a sizable fraction (often over 50%) of the distortion energy is associated with bending the X-Y-Z bond of the dipole, consistent with their earlier work suggesting the importance of this vibration in attaining and crossing the TS. What’s new in this paper is the extensive MD studies, with trajectory studies of all 18 reactions. These revealed again the importance of vibrational energy in this X-Y-Z bending mode in crossing the TS. They also noted the role of translational energy, and the relationship between translational vs. vibrational energy depending on the early/late nature of the TS. Their final point was that the lifetime of any diradical or diradical-like intermediate is so short, less than the time of a bond vibration, so that one can discount any diradical participation. The reaction is concerted.

References

(1) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloadditions: Energy Partitioning of Reactants and Quantitation of Synchronicity," J. Am. Chem. Soc., 2010, ASAP, DOI: /10.1021/ja909372f

(2) Xu, L.; Doubleday, C. E.; Houk, K. N., "Dynamics of 1,3-Dipolar Cycloaddition Reactions of Diazonium Betaines to Acetylene and Ethylene: Bending Vibrations Facilitate Reaction," Angew. Chem. Int. Ed., 2009, 48, 2746-2748, DOI: 10.1002/anie.200805906

The nature of reactions of indolynes is the subject of two recent computational/experimental studies. There are three isomeric indolynes 1a-c which are analogues of the more famous benzyne (which I discuss in significant detail in Chapter 4.4 of my book).

One might anticipate that the indolynes undergo comparable reactions as benzyne, like Diels-Alder reactions and nucleophilic attack. In fact the indolynes do undergo these reactions, with unusual regiospecificity. For example, the reaction of the substituted 6,7-indolyne undergoes regioselective Diels-Alder cycloaddition with substituted furans (Scheme 1), but the reaction with the other indolynes gives no regioselection. ¹ Note that the preferred product is the more sterically congested adduct.

Scheme 1

In the case of nucleophilic addition, the nucleophiles add specifically to C₆ with substituted 6,7-indolynes (Scheme 2), while addition to 4,5-indolynes preferentially gives the C₅-adduct (greater than 3:1) while addition to the 5,6-indolynes preferentially gives the C₅-adduct), but with small selectivity (less than 3:1).²

Scheme 2

The authors of both papers – Chris Cramer studied the Diels-Alder chemistry and Ken Houk studied the nucleophilic reactions – employed DFT computations to examine the activation barriers leading to the two regioisomeric products. So for example, Figure 1 shows the two transition states for the reaction of 2c with 2-iso-propyl furan computed at MO6-2X/6-311+G(2df,p).

ΔG‡ = 9.7

ΔG‡ = 7.6

Figure 1. MO6-21/6-311+G(2df,p) optimized TSs for the reaction of 2-iso-propylfuran with 2c. Activation energy (kcal mol^-1) listed below each structure.¹

The computational results are completely consistent with the experiments. For the Diels-Alder reaction of 2-t-butylfuran with the three indolynes 2a-c, the lower computed TS always corresponds with the experimentally observed major product. The difference in the energy of the TSs leading to the two regioisomers for reaction with 2a and 2b is small (less than 1 kcal mol^-1), consistent with the small selectivity. On the other hand, no barrier could be found for the reaction of 2-t-butylfuran with 2c that leads to the major product. Similar results are also obtained for the nucleophilic addition – in all cases, the experimentally observed major product corresponds with the lower computed activation barrier.

So what accounts for the regioselectivity? Both papers make the same argument, though couched in slightly different terms. Houk argues in terms of distortion energy – the energy needed to distort reactants to their geometries in the TS. As seen in Figure 2, the benzyne fragment of 2a is distorted, with the C-C-C angle at C₄ of 125° and at C₅ of 129°. In the transition states, the angle at the point of nucleophilic attack widens. Since the angle starts out wider at C₅, attack there is preferred, since less distortion is needed to achieve the geometry of the TS.

2a
TS at C4 ΔG‡ = 12.9	TS at C5 ΔG‡ = 9.9

Figure 2. B3LYP/6-31G(d) optimized structures of 2a and the TSs for the reaction of aniline with 2a. Activation energy in kcal mol^-1.²

Cramer argues in terms of the indolyne acting as an electrophile. Increasing substitution at the furan 2-position makes is better at stabilizing incipient positive charge that will build up there during a (very) asymmetric Diels-Alder transition state. This explains the increasing selectivity of the furan with increasing substitution. The indolyne acting as an electrophile means that the attack will lead from the center will lesser charge. In 2c, the C-C-C angle at C₆ is 135.3°, while that at C₇ is 117.2°. This makes C₇ more carbanionic and C₆ more carbocationic; therefore, the first bond made is to C₆, leading to the more sterically congested product. Note that Houk’s argument applies equally well, as C₆ is predistorted to the TS geometry.

References

(1) Garr, A. N.; Luo, D.; Brown, N.; Cramer, C. J.; Buszek, K. R.; VanderVelde, D., "Experimental and Theoretical Investigations into the Unusual Regioselectivity of 4,5-, 5,6-, and 6,7-Indole Aryne Cycloadditions," Org. Lett., 2010, 12, 96-99, DOI: 10.1021/ol902415s

(2) Cheong, P. H. Y.; Paton, R. S.; Bronner, S. M.; Im, G. Y. J.; Garg, N. K.; Houk, K. N., "Indolyne and Aryne Distortions and Nucleophilic Regioselectivites," J. Am. Chem. Soc., 2010, 132, 1267-1269, DOI: 10.1021/ja9098643

InChIs

1a: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h2,4-6,9H
InChIKey=RNDHGGYOIRREHC-UHFFFAOYAU

1b: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h3-6,9H
InChIKey=WWZQFJXNXMIWCD-UHFFFAOYAO

1c: InChI=1/C8H5N/c1-2-4-8-7(3-1)5-6-9-8/h1,3,5-6,9H
InChIKey=UHIRLIIPIXHWLT-UHFFFAOYAH

2a: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h3,5-7H,1H3
InChIKey=VTVUPAJGRVFCKI-UHFFFAOYAJ

2b: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h4-7H,1H3
InChIKey=KKPOWDDYMOXTFW-UHFFFAOYAN

2c: InChI=1/C9H7N/c1-10-7-6-8-4-2-3-5-9(8)10/h2,4,6-7H,1H3
InChIKey=MDAHOGWZOBLIEX-UHFFFAOYAZ

Not particularly strong programming at the year’s spring ACS meeting – but one great session in the organic division yesterday. This was the awards session in honor of John Baldwin getting the James Flack Norris Award for physical organic chemistry.

First to speak was James Duncan, who discussed his recent CASSCF computations looking for pseudopericylic [3,3]-sigmatropic migrations. I will be commenting on his latest work in a post that will appear soon.

I had to skip the next talk, but came back to hear John Brauman discuss recent work on the solvation effect in the S_N2 reaction. This is an interesting case of where the screening of larger substituents is counterbalanced by geometric changes that lead to greater charge distribution. The net effect is that they cancel each other out, and the methyl,ethyl, iso-propyl, butyl β-effect is negligible.

Next was Peter Schreiner who discussed his carbene work, specifically the enormous tunneling effect observed in hydroxymethylene (see this post). He discussed some new work, that is if anything even more fantastic on methylhydroxycarbene – look for this work perhaps later in 2011.

Last to speak was John Baldwin – and he described his truly tour de force efforts in examining the [1,3]-rearrangements of vinylcyclopropane and vinylcyclobutane. The former work is described in my book, while the later study is still ongoing.

John’s work is amazingly painstaking and careful. I am truly in awe of his dedication in taking on extremely difficult studies that require enormous care. John has really taught us a lot – not just about these rearrangements (they involve diradicals on a flat plateau demanding dynamic analysis – but how to think about a study and then carry it out to fruition so that all details are assessed. A truly deserving recipient!

Houk has performed a very nice examination of the performance of some density functionals.¹ He takes a quite different approach than what was proposed by Grimme – the “mindless” benchmarking² using random molecules (see this post). Rather, Houk examined a series of simple aldol, Mannich and α-aminoxylation reactions, comparing their reaction energies predicted with DFT against that predicted with CBQ-QB3. The idea here is to benchmark DFT performance for simple reactions of specific interest to organic chemists. These reactions are of notable current interest due their involvement in organocatalytic enantioselective chemistry (see my posts on the aldol, Mannich, and Hajos-Parrish-Eder-Sauer-Wiechert reaction). Examples of the reactions studied (along with their enthalpies at CBS-QB3) are Reaction 1-3.

For the four simple aldol reactions and four simple Mannich reactions, PBE1PBE,
mPW1PW91 and MO6-2X all provided reaction enthalpies with errors of about 2 kcal mol^-1. The much maligned B3LYP functional, along with B3PW91 and B1B95 gave energies with significant larger errors. For the three α-aminoxylation reactions, the errors were better with B3PW91 and B1B95 than with PBE1PBE or MO6-2X. Once again, it appears that one is faced with finding the right functional for the reaction under consideration!

Of particular interest is the decomposition of these reactions into related isogyric, isodesmic
and homdesmic reactions. So for example Reaction 1 can be decomposed into Reactions 4-7 as shown in Scheme 1. (The careful reader might note that these decomposition reactions are isodesmic and homodesmotic and hyperhomodesmotic reactions.) The errors for Reactions 4-7 are typically greater than 4 kcal mol^-1 using B3LYP or B3PW91, and even with MO6-2X the errors are about 2 kcal mol^-1.

Scheme 1.

Houk also points out that Reactions 4, 8 and 9 (Scheme 2) focus on having similar bond changes as in Reactions 1-3. And it’s here that the results are most disappointing. The errors produced by all of the functionals for Reactions 4,8 and 9 are typically greater than 2 kcal mol^-1, and even MO2-6x can be in error by as much as 5 kcal mol^-1. It appears that the reasonable performance of the density functionals for the “real world” aldol and Mannich reactions relies on fortuitous cancellation of errors in the underlying reactions. Houk calls for the development of new functionals designed to deal with fundamental simple bond changing reactions, like the ones in Scheme 2.

Scheme 2

References

(1) Wheeler, S. E.; Moran, A.; Pieniazek, S. N.; Houk, K. N., "Accurate Reaction Enthalpies and Sources of Error in DFT Thermochemistry for Aldol, Mannich, and α-Aminoxylation Reactions," J. Phys. Chem. A 2009, 113, 10376-10384, DOI: 10.1021/jp9058565

(2) Korth, M.; Grimme, S., ""Mindless" DFT Benchmarking," J. Chem. Theory Comput. 2009, 5, 993–1003, DOI: 10.1021/ct800511q