What is required in order to compute very accurate NMR chemical shifts? Harding, Gauss and Schleyer take on the interesting spectrum of 1-adamantyl cation to try to discern the important factors in computing its 13C and 1H chemical shifts.1
1
To start, the chemical shifts of 1-adamtyl cation were computed at B3LYP/def2-QZVPP and
MP2/qz2p//MP2/cc-pVTZ. The root means square error (compared to experiment) for the carbon chemical shifts is large: 12.76 for B3LYP and 6.69 for MP2. The proton shifts are predicted much more accurately with an RMS error of 0.27 and 0.19 ppm, respectively.
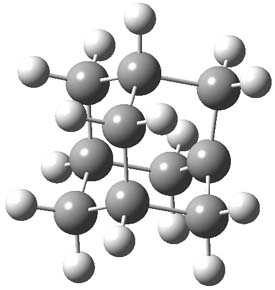
The authors speculate that the underlying cause of the poor prediction is the geometry of the molecule. The structure of 1 was optimized at HF/cc-pVTZ, MP2/cc-pVTZ and CCSD(T)/pVTZ and then the chemical shifts were computed using MP2/tzp with each optimized geometry. The RMS error of the 12C chemical shifts are HF/cc-pVTZ: 9.55, MP2/cc-pVTZ: 5.62, and CCSD(T)/pVTZ: 5.06. Similar relationship is seen in the proton chemical shifts. Thus, a better geometry does seem to matter. The CCSD(T)/pVTZ optimized structure of 1 is shown in Figure 1.
|
1 |
Figure 1. CCSD(T)/pVTZ optimized structure of 1.
Unfortunately, the computed chemical shifts at CCSD(T)/qz2p//CCSD(T)/cc-pVTZ are still in error; the RMS is 4.78ppm for the carbon shifts and 0.26ppm for the proton shifts. Including a correction for the zero-point vibrational effects and adjusting to a temperature of 193 K to match the experiment does reduce the error; now the RMS for the carbon shifts is 3.85 ppm, with the maximum error of 6 ppm for C3. The RMS for the proton chemical shifts is 0.21ppm.
The remaining error they attribute to basis set incompleteness in the NMR computation, a low level treatment of the zero-point vibrational effects (which were computed at HF/tz2p), neglect of the solvent, and use of a reference in the experiment that was not dissolved in the same media as the adamantyl cation.
So, to answer our opening question – it appears that a very good geometry and treatment of vibrational effects is critical to accurate NMR shift computation of this intriguing molecule. Let the
computational chemist beware!
References
(1) Harding, M. E.; Gauss, J.; Schleyer, P. v. R., "Why Benchmark-Quality Computations Are Needed To Reproduce 1-Adamantyl Cation NMR Chemical Shifts Accurately," J. Phys. Chem. A, 2011, 115, 2340-2344, DOI: 10.1021/jp1103356
InChI
1: InChI=1/C10H15/c1-7-2-9-4-8(1)5-10(3-7)6-9/h7-9H,1-6H2/q+1
InChIKey=HNHINQSSKCACRU-UHFFFAOYAC

Henry Rzepa responded on 21 Jul 2011 at 12:51 am #
Harding, Gauss and Schleyer methodically go through a variety of sources of error for comparing calculated and experimental carbon NMR shifts, some of which are described above. Having scanned the paper, I was surprised to find no reference to the counter ion (or its absence) as another potential source of error. Although “non-coordinating” counterions are used to generate stable solutions of carbocations, it is easy to imagine that it would adopt a relatively fixed probable position with respect to the cation, and that this would therefore perturb the various shifts. The accepted wisdom is that the counterion does not influence the shifts very much at all (< 1ppm), but I have always found that surprising. It is certainly possible nowadays to include such an anion in the calculation (see for example here) to eg eliminate its presence as a contributor to the errors noted above.
I will have a go and report back!
Henry Rzepa responded on 22 Jul 2011 at 6:44 am #
I commented earlier that no account of the ion-pair had been taken into account in the predictions of the NMR spectra of adamantyl cation. so I perfomed a cheap and simple calculation, B3LYP/cc-pVTZ/SCRF ε=8.93 or ε=181.56 using SnCl5- as the counterion. The C(+)…Sn distance came out at around 5.0Å. I did “massage” slightly, in the sense that a calculation of TMS using the same computational model would not have included the counter-ion in the model. Instead, the TMS reference was adjusted by 6.4 ppm for all the carbon shifts only (its possible the TMS was an external reference in the experiment anyway). The results came out as below. To summarise (I am not sure one can put HTML tables into the comments on Steve’s Blog), the ion-pair B3LYP model is no worse than the “kitchen sink” gas phase model.
The obvious conclusion is that one can get a good fit to expt by either increasing the quality of the theory to a very high level, but ignoring the solvent and counter-ion, or by using a very modest level of theory which however does include the counter-ion and a continuum solvent of high polarity. Is this a case of (one or other of the two approaches) getting the “right” answer for the wrong reasons? Of course the only way to settle this is to combine the two approaches (easier said than done). Another comment would be that the description of the counter-ion (which probably does not match that actually used) needs improving. And one can do better than the B3LYP functional at no extra cost.
What might be worth concluding is the days of gas-phase simulations (no matter how accurate) for predicting solution properties may be numbered!
Extreme chemical intimacy: the Xe2@C60 ion-pair. « Henry Rzepa responded on 03 Aug 2011 at 11:09 am #
[…] (b) if the outer skeleton does indeed absorb electrons, a (continuum) solvation correction may also influence the properties. This was done as a ωB97XD/cc-pVDZ/SCRF=water calculation, with aug-cc-pVDZ-pp on […]
The importance of being complete. « Henry Rzepa responded on 26 Sep 2011 at 2:05 am #
[…] Well, here I add it in to complete the model, using perchlorate. I was following in a sense my own advice on Steve Bachrach’s blog, where the NMR spectrum of the adamantly cation was discussed. I had argued there that the anion (I […]