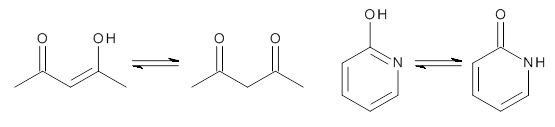
The role of dispersion in organic chemistry has been slowly recognized as being quite critical in a variety of systems. I have blogged on this subject many times, discussing new methods for properly treating dispersion within quantum computations along with a variety of molecular systems where dispersion plays a critical role. Schreiner¹ has recently published a very nice review of molecular systems where dispersion is a key component towards understanding structure and/or properties.

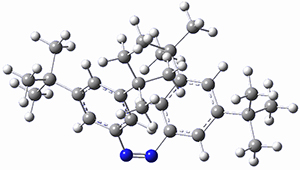
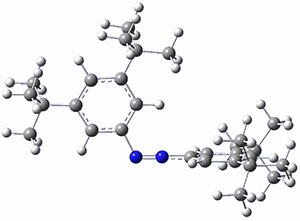
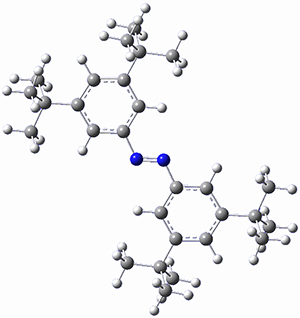
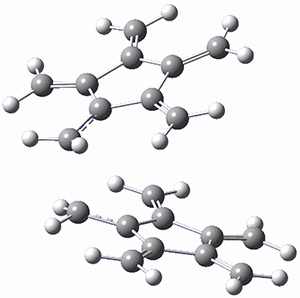
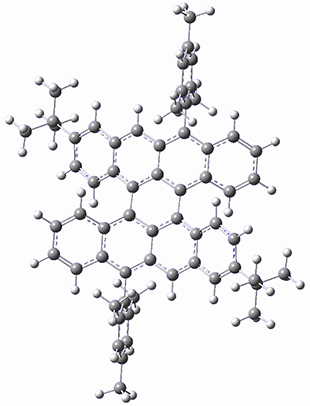
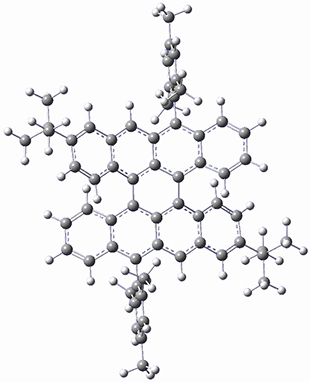
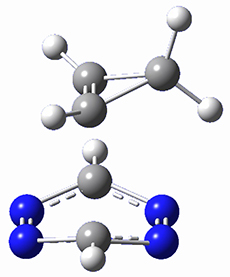
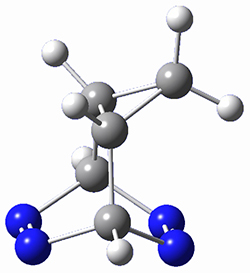
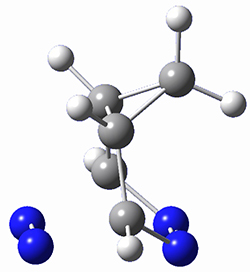
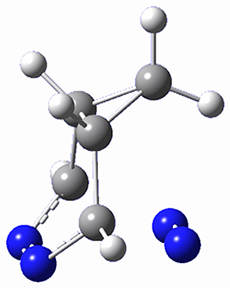
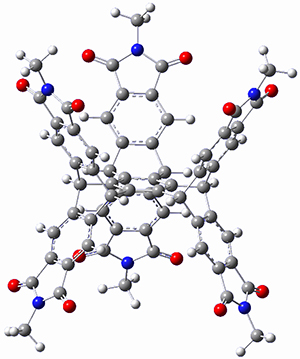
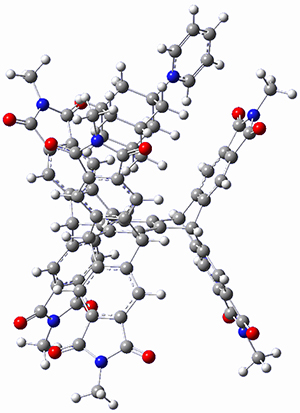
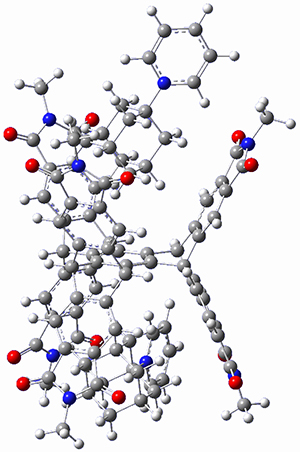
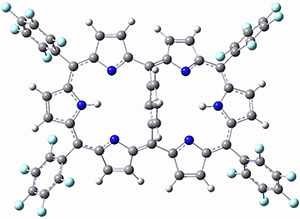
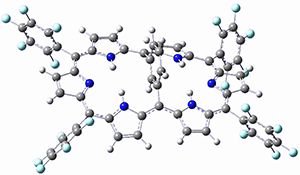
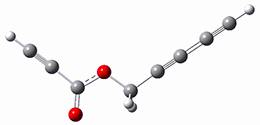
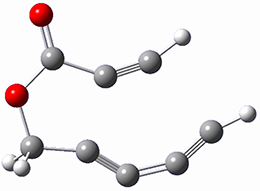
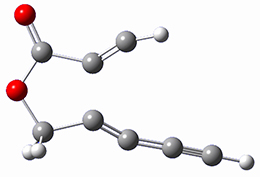
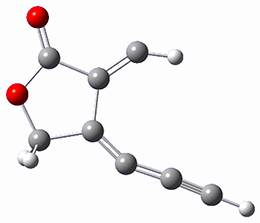
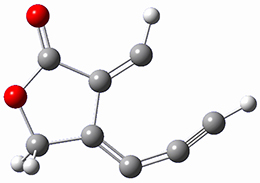
In a similar vein, Wegner and coworkers have examined the Z to E transition of azobenzene systems (1a-g → 2a-g) using both experiment and computation.² They excited the azobenzenes to the Z conformation and then monitored the rate for conversion to the E conformation. In addition they optimized the geometries of the two conformers and the transition state for their interconversion at both B3LYP/6-311G(d,p) and B3LYP-D3/6-311G(d,p). The optimized structure of the t-butyl-substituted system is shown in Figure 1.

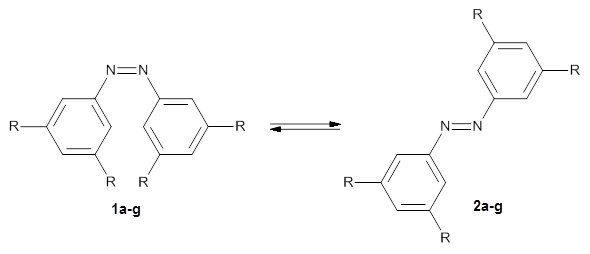
a: R=H; b: R=tBu; c: R=Me; d: R=iPr; e: R=Cyclohexyl; f: R=Adamantyl; g: R=Ph

1b

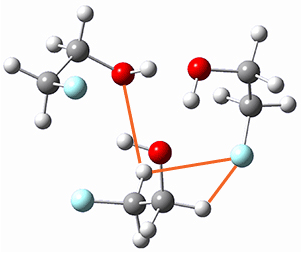
1b-TS-2b

2b

Figure 1. B3LYP-D3/6-311G(d,p) optimized geometries of 1a, 2a, and the TS connecting them.

The experiment finds that the largest activation barriers are for the adamantly 1f and t-butyl 1b azobenzenes, while the lowest barriers are for the parent 1a and methylated 1c azobenzenes.

The trends in these barriers are not reproduced at B3LYP but are reproduced at B3LYP-D3. This suggests that dispersion is playing a role. In the Z conformations, the two phenyl groups are close together, and if appropriately substituted with bulky substituents, contrary to what might be traditionally thought, the steric bulk does not destabilize the Z form but actually serves to increase the dispersion stabilization between these groups. This leads to a higher barrier for conversion from the Z conformer to the E conformer with increasing steric bulk.

References

(1) Wagner, J. P.; Schreiner, P. R. "London Dispersion in Molecular Chemistry—Reconsidering Steric Effects," Angew. Chem. Int. Ed. 2015, 54, 12274-12296, DOI: 10.1002/anie.201503476.

(2) Schweighauser, L.; Strauss, M. A.; Bellotto, S.; Wegner, H. A. "Attraction or Repulsion? London Dispersion Forces Control Azobenzene Switches," Angew. Chem. Int. Ed. 2015, 54, 13436-13439, DOI: 10.1002/anie.201506126.

InChIs

1b: InChI=1S/C28H42N2/c1-25(2,3)19-13-20(26(4,5)6)16-23(15-19)29-30-24-17-21(27(7,8)9)14-22(18-24)28(10,11)12/h13-18H,1-12H3/b30-29-
InChIKey=SOCNVTNVHBWFKC-FLWNBWAVSA-N

2b: InChI=1S/C28H42N2/c1-25(2,3)19-13-20(26(4,5)6)16-23(15-19)29-30-24-17-21(27(7,8)9)14-22(18-24)28(10,11)12/h13-18H,1-12H3/b30-29+
InChIKey=SOCNVTNVHBWFKC-QVIHXGFCSA-N

What may be something of a surprise, [5]radialene 1 has only just now been synthesized.¹ What makes this especially intriguing is that [3]radialene 2, [4]radialene 3 and [6]radialene 4 have been known for years.

Paddon-Row, Sherburn, and coworkers speculated that [5]radialene must undergo polymerization much more rapidly than the other radialenes. They computed the activation barrier for the Diels-Alder dimerization of the radialenes at G4(MP2). (The optimized structure of 1 and the transition state for the dimerization of 1 are shown in Figure 1.) The activation barrier for the dimerization of 1 is computed to be only 14.3 kJ mol^-1, much lower than for the dimerization of 3 (59.2 kJ mol^-1) or 4 (31.5 kJ mol^-1).

1

TS

Figure 1. G4(MP2) optimized geometries of 1 and the TS for the dimerization of 1.

Application of the distortion/interaction energy model helps to understand why 1 is the outlier among the radialenes. The distortion energy to bring two molecules of 1 to the transition state geometry is about 63 kJ mol^-1, and this is much less than for [4]radialene (102 kJ mol^-1) or [6]radialene (96 kJ mol^-1). The reason lies in that [5]radialene is close to planarity and so only the pyramidalization at one carbon is necessary to reach the TS geometry. For 4, which is in a chair geometry, significant distortion is needed to bring the double bonds into conjugation. For 3, the high distortion energy is due to the significant pyramidalization energy needed.

Another interesting note is that the TSs for the Diels-Alder reactions of the radialenes is bis-pericyclic. The authors point out that dynamic effects may be important – though they did not perform any MD studies.

These computations drove the synthesis of 1 by coordinating it to two equivalents of Fe(CO)₃ and then driving off the metals with cerium ammonium nitrate in acetone at -78 °C. The free [5]radialene was then detected by NMR, and it decomposes with a half-life of about 16 min at -20 °C.

References

(1) Mackay, E. G.; Newton, C. G.; Toombs-Ruane, H.; Lindeboom, E. J.; Fallon, T.; Willis, A. C.; Paddon-Row, M. N.; Sherburn, M. S. "[5]Radialene," J. Am. Chem. Soc. 2015, 137, 14653–14659, DOI: 10.1021/jacs.5b07445.

InChIs

1: InChI=1S/C10H10/c1-6-7(2)9(4)10(5)8(6)3/h1-5H2
InChIKey=RVBXYBDJWKWCLW-UHFFFAOYSA-N

Capturing buckyballs involves molecular design based on non-covalent interactions. This poses interesting challenges for both the designer and the computational chemist. The curved surface of the buckyball demands a sequestering agent with a complementary curved surface, likely an aromatic curved surface to facilitate π-π stacking interactions. For the computational chemist, weak interactions, like dispersion and π-π stacking demand special attention, particularly density functionals designed to account for these interactions.

Two very intriguing new buckycatchers were recently prepared in the Sygula lab, and also examined by DFT.¹ Compounds 1 and 2 make use of the scaffold developed by Klärner.² In these two buckycatchers, the tongs are corranulenes, providing a curved aromatic surface to match the C₆₀ and C₇₀ surface. They differ in the length of the connector unit.

B97-D/TZVP computations of the complex of 1 and 2 with C₆₀ were carried out. The optimized structures are shown in Figure 1. The binding energies (computed at B97-D/QZVP*//B97-D/TZVP) of these two complexes are really quite large. The binding energy for 1:C₆₀ is 33.6 kcal mol^-1, comparable to some previous Buckycatchers, but the binding energy of 2:C₆₀ is 50.0 kcal mol^-1, larger than any predicted before.

1

2

Figure 1. B97-D/TZVP optimized geometries of 1:C₆₀and 2:C₆₀.

Measurement of the binding energy using NMR was complicated by a competition for one or two molecules of 2 binding to buckyballs. Nonetheless, the experimental data show 2 binds to C₆₀ and C₇₀ more effectively than any previous host. They were also able to obtain a crystal structure of 2:C₆₀.

References

(1) Abeyratne Kuragama, P. L.; Fronczek, F. R.; Sygula, A. "Bis-corannulene Receptors for Fullerenes Based on Klärner’s Tethers: Reaching the Affinity Limits," Org. Lett. 2015, ASAP, DOI: 10.1021/acs.orglett.5b02666.

(2) Klärner, F.-G.; Schrader, T. "Aromatic Interactions by Molecular Tweezers and Clips in Chemical and Biological Systems," Acc. Chem. Res. 2013, 46, 967-978, DOI: 10.1021/ar300061c.

InChIs

1: InChI=1S/C62H34O2/c1-63-61-57-43-23-45(41-21-37-33-17-13-29-9-5-25-3-7-27-11-15-31(35(37)19-39(41)43)53-49(27)47(25)51(29)55(33)53)59(57)62(64-2)60-46-24-44(58(60)61)40-20-36-32-16-12-28-8-4-26-6-10-30-14-18-34(38(36)22-42(40)46)56-52(30)48(26)50(28)54(32)56/h3-22,43-46H,23-24H2,1-2H3/t43-,44+,45+,46-
InChIKey=RLOJCVYXCBOUQB-RYSLUOGPSA-N

2: InChI=1S/C66H36O2/c1-67-65-51-24-45-43-23-44(42-20-38-34-16-12-30-8-4-27-3-7-29-11-15-33(37(38)19-41(42)43)59-55(29)53(27)56(30)60(34)59)46(45)25-52(51)66(68-2)64-50-26-49(63(64)65)47-21-39-35-17-13-31-9-5-28-6-10-32-14-18-36(40(39)22-48(47)50)62-58(32)54(28)57(31)61(35)62/h3-22,24-25,43-44,49-50H,23,26H2,1-2H3/t43-,44+,49+,50-
InChIKey=JAUUHTKCNSNBMD-NETXOKAWSA-N

Feng, Müller and co-workers have prepared a bistetracene analogue 1.¹ This molecule displays some interesting features. While a closed shell Kekule structure can be written, a biradical structure results in more closed Clar rings, suggesting that perhaps the molecule is a ground state singlet biradical. The loss of NMR signals with increasing temperature along with an EPR signal that increases with temperature both support the notion of a ground state singlet biradical with a triplet excited state. The EPR measurement suggest as singlet-triplet gap of 3.4 kcal mol^-1.

The optimized B3LYP/6-31G(d,p) geometries of the biradical singlet and triplet states are shown in Figure 1. The singlet is lower in energy by 6.7 kcal mol^-1. The largest spin densities are on the carbons that carry the lone electron within the diradical-type Kekule structures.

singlet 1

triplet 1

Figure 1. B3LYP/6-31G(d,p) optimized geometries of the biradical singlet and triplet states of 1.

References

(1) Liu, J.; Ravat, P.; Wagner, M.; Baumgarten, M.; Feng, X.; Müllen, K. "Tetrabenzo[a,f,j,o]perylene: A Polycyclic Aromatic Hydrocarbon With An Open-Shell Singlet Biradical Ground State," Angew. Chem. Int. Ed. 2015, 54, 12442-12446, DOI: 10.1002/anie.201502657.

InChIs

1: InChI=1S/C62H56/c1-33-25-35(3)51(36(4)26-33)53-45-17-13-15-19-47(45)57-56-44-24-22-42(62(10,11)12)30-40(44)32-50-54(52-37(5)27-34(2)28-38(52)6)46-18-14-16-20-48(46)58(60(50)56)55-43-23-21-41(61(7,8)9)29-39(43)31-49(53)59(55)57/h13-32H,1-12H3
InChIKey=LPRMROONCKWUEJ-UHFFFAOYSA-N

Houk and Doubleday report yet another example of dynamic effects in reactions that appear to be simple, ordinary organic reactions.¹ Here they look at the Diels-Alder reaction of tetrazine 1 with cyclopropene 2. The reaction proceeds by first crossing the Diels-Alder transition state 3 to form the intermediate 4. This intermediate can then lose the anti or syn N₂, through 5a or 5s, to form the product 6. The structures and relative energies, computed at M06-2X/6-31G(d), of these species are shown in Figure 1.

3 17.4	4 -33.2
5a -28.9	5s -20.0
6 -86.2

Figure 1. M06-2X/6-31G(d) optimized geometries and energies (relative to 1 + 2) of the critical points along the reaction of tetrazine with cyclopropene.

The large difference in the activation barriers between crossing 5a and 5s (nearly 9 kcal mol^-1) suggests, by transition state theory, a preference of more than a million for loss of the anti N₂ over the syn N₂. However, quasiclassical trajectory studies, using B3LYP/6-31G(d), finds a different situation. The anti pathway is preferred, but only by a 4:1 ratio! This dynamic effect arises from a coupling of the v₃ mode which involves a rocking of the cyclopropane ring that brings a proton near the syn N₂ functionality, promoting its ejection. In addition, the trajectory studies find short residence times within the intermediate neighborhood for the trajectories that lead to the anti product and longer residence times for the trajectories that lead to the syn product. All together, a very nice example of dynamic effects playing a significant role in a seemingly straightforward organic reaction.

References

(1) Törk, L.; Jiménez-Osés, G.; Doubleday, C.; Liu, F.; Houk, K. N. "Molecular Dynamics of the Diels–Alder Reactions of Tetrazines with Alkenes and N₂ Extrusions from Adducts," J. Am. Chem. Soc. 2015, 137, 4749-4758, DOI: 10.1021/jacs.5b00014.

InChIs

1: InChI=1S/C2H2N4/c1-3-5-2-6-4-1/h1-2H
InChIKey=HTJMXYRLEDBSLT-UHFFFAOYSA-N

2: InChI=1S/C3H4/c1-2-3-1/h1-2H,3H2
InChIKey=OOXWYYGXTJLWHA-UHFFFAOYSA-N

4: InChI=1S/C5H6N4/c1-2-3(1)5-8-6-4(2)7-9-5/h2-5H,1H2
InChIKey=JGSMBFYJCNPYDM-UHFFFAOYSA-N

6: InChI=1S/C5H6N2/c1-4-2-6-7-3-5(1)4/h2-5H,1H2
InChIKey=RYJFHKGQZKUXEH-UHFFFAOYSA-N

Badjic, Hadad, and coworkers have prepared ¹ an interesting host molecule that appears like two cups joined at the base, with one cup pointed up and the other pointed down. A slightly simplified analogue 1 of the synthesized host is shown in Figure 1. The actual host is found to bind one molecule of 2, but does not appear to bind a second molecule. Seemingly, only one of the cups can bind a guest, and that this somehow deters a second guest from being bound into the other cup.

Figure 1. B3LYP/6-31G* optimized geometry of host molecule 1. (Visualization of this molecules and the structures below are greatly enhanced by clicking on each image which will invoke the molecular viewer Jmol.)

To address negative allosterism, the authors optimized the structure of 1 at B3LYP/6-31G* (shown in Figure 1). They then optimized the geometry with the constraint that the three arms in the top cup were ever more slightly moved inward. This had the consequential effect of moving the three arms of the bottom cup farther apart. They next optimized (at M06-2x/6-31G(d)) the structures of 1 holding one molecule of guest 2 and with two molecules of guest 2. These structures are shown in Figure 2. In the structure with one guest, the arms are brought in towards the guest for the cup where the guest is bound, and this consequently draws the arms in the other cup to be farther apart, and thereby less capable of binding a second guest. The structure with two guest shows that the arms are not able to get sufficiently close to either guest to form strong non-covalent interactions.

Figure 2. M06-2x/6-31G(d) optimized structures of 1 with one or two molecules of 2.

Thus, the negative allosterism results from a geometric change created by the induced fit of the first guest that results in an unfavorable environment for a second guest.

References

(1) Chen, S.; Yamasaki, M.; Polen, S.; Gallucci, J.; Hadad, C. M.; Badjić, J. D. "Dual-Cavity Basket Promotes Encapsulation in Water in an Allosteric Fashion," J. Am. Chem. Soc. 2015, 137, 12276-12281, DOI: 10.1021/jacs.5b06041.

What is the relationship between a ground state and the first excited triplet (or first excited singlet) state regarding aromaticity? Baird¹ argued that there is a reversal, meaning that a ground state aromatic compound is antiaromatic in its lowest triplet state, and vice versa. It is suggested that the same reversal is also true for the second singlet (excited singlet) state.

Osuka, Sim and coworkers have examined the geometrically constrained hexphyrins 1 and 2.² 1 has 26 electrons in the annulene system and thus should be aromatic in the ground state, while 2, with 28 electrons in its annulene system should be antiaromatic. The ground state and lowest triplet structures, optimized at B3LYP/6-31G(d,p), of each of them are shown in Figure 1.

11	12
31	32

Figure 1. B3LYP/6-31G(d,p) optimized geometries of 1 and 2.

NICS computations where made in the centers of each of the two rings formed by the large macrocycle and the bridging phenyl group (sort of in the centers of the two lenses of the eyeglass). The NICS values for 1 are about -15ppm, indicative of aromatic character, while they are about +15ppm for 2, indicative of antiaromatic character. However, for the triplet states, the NICS values change sign, showing the aromatic character reversal between the ground and excited triplet state. The aromatic states are also closer to planarity than the antiaromatic states (which can be seen by clicking on the images in Figure 1, which will launch the JMol applet so that you can rotate the molecular images).

They also performed some spectroscopic studies that support the notion of aromatic character reversal in the excited singlet state.

References

(1) Baird, N. C. "Quantum organic photochemistry. II. Resonance and aromaticity in the lowest ³ππ* state of cyclic hydrocarbons," J. Am. Chem. Soc. 1972, 94, 4941-4948, DOI: 10.1021/ja00769a025.

(2) Sung, Y. M.; Oh, J.; Kim, W.; Mori, H.; Osuka, A.; Kim, D. quot;Switching between Aromatic and Antiaromatic 1,3-Phenylene-Strapped [26]- and [28]Hexaphyrins upon Passage to the Singlet Excited State," J. Am. Chem. Soc. 2015, 137, 11856-11859, DOI: 10.1021/jacs.5b04047.

InChIs

1: InChI=1S/C60H18F20N6/c61-41-37(42(62)50(70)57(77)49(41)69)33-23-8-4-19(81-23)31-17-2-1-3-18(16-17)32(21-6-10-25(83-21)35(29-14-12-27(33)85-29)39-45(65)53(73)59(79)54(74)46(39)66)22-7-11-26(84-22)36(40-47(67)55(75)60(80)56(76)48(40)68)30-15-13-28(86-30)34(24-9-5-20(31)82-24)38-43(63)51(71)58(78)52(72)44(38)64/h1-16,85-86H/b31-19+,31-20+,32-21+,32-22+,33-23+,33-27+,34-24+,34-28+,35-25+,35-29+,36-26+,36-30+
InChIKey=TUOMWLSCXXODFY-CQGNQUHXSA-N

2: InChI=1S/C60H20F20N6/c61-41-37(42(62)50(70)57(77)49(41)69)33-23-8-4-19(81-23)31-17-2-1-3-18(16-17)32(21-6-10-25(83-21)35(29-14-12-27(33)85-29)39-45(65)53(73)59(79)54(74)46(39)66)22-7-11-26(84-22)36(40-47(67)55(75)60(80)56(76)48(40)68)30-15-13-28(86-30)34(24-9-5-20(31)82-24)38-43(63)51(71)58(78)52(72)44(38)64/h1-16,81-84H/b31-19+,31-20+,32-21+,32-22+,33-23+,33-27+,34-24+,34-28+,35-25+,35-29+,36-26+,36-30+
InChIKey=KTIAGNMFTAGKFJ-CQGNQUHXSA-N

Here is another fine example of the power of combining experiment and computation. Xu and co-worker has applied the FT microwave technique, which has been used in conjunction with computation by the Alonso group (especially) as described in these posts, to the trimer of 2-fluoroethanol.¹ They computed a number of trimer structures at MP2/6-311++G(2d,p) in an attempt to match up the computed spectroscopic constants with the experimental constants. The two lowest energy structures are shown in Figure 1. The second lowest energy structure has nice symmetry, but it does not match up well with the experimental spectra. However, the lowest energy structure is in very good agreement with the experiments.

(0.0)

(4.15)

Table 1. MP2/6-311++G(2d,p) optimized structures and relative energies (kJ mol^-1) of the two lowest energy structures of the trimer of 2-fluoroethanol. The added orange lines in the lowest energy structure denote the bifurcated hydrogen bonds identified by QTAIM.

Of particular note is that topological electron density analysis (also known as quantum theoretical atoms in a molecule, QTAIM) of the wavefunction of the lowest energy structure of the trimer identifies two hydrogen bond bifurcations. The authors suggest that these additional interactions are responsible, in part, for the stability of this lowest energy structure.

References

(1) Thomas, J.; Liu, X.; Jäger, W.; Xu, Y. "Unusual H-Bond Topology and Bifurcated H-bonds in the 2-Fluoroethanol Trimer," Angew. Chem. Int. Ed. 2015, 54, 11711-11715, DOI: 10.1002/anie.201505934.

InChIs

2-fluoroethanol: InChI=1S/C2H5FO/c3-1-2-4/h4H,1-2H2, InChIKey=GGDYAKVUZMZKRV-UHFFFAOYSA-N

The keto-enol tautomerization is a fundamental concept in organic chemistry, taught in the introductory college course. As such, it provides an excellent test reaction to benchmark the performance computational methods. Acevedo and colleagues have reported just such a benchmark study.¹

First, the compare a wide variety of methods, ranging from semi-empirical, to DFT, and to composite procedures, with experimental gas-phase free energy of tautomerization. They use seven such examples, two of which are shown in Scheme 1. The best results from each computation category are AM1, with a mean absolute error (MAE) of 1.73 kcal mol^-1, M06/6-31+G(d,p), with a MAE of 0.71 kcal mol^-1, and G4, with a MAE of 0.95 kcal mol^-1. All of the modern functionals do a fairly good job, with MAEs less than 1.3 kcal mol^-1.

Scheme 1

As might be expected, the errors were appreciably larger for predicting the free energy of tautomerization, with a good spread of errors depending on the method for handling solvent (PCM, CPCM, SMD) and the choice of cavity radius. The best results were with the G4/PCM/UA0 procedure, though M06/6-31+G(d,p)/PCM and either UA0 or UFF performed quite well, at considerably less computational expense.

References

(1) McCann, B. W.; McFarland, S.; Acevedo, O. "Benchmarking Continuum Solvent Models for Keto–Enol Tautomerizations," J. Phys. Chem. A 2015, 119, 8724-8733, DOI: 10.1021/acs.jpca.5b04116.

Cramer, Hoye, Kuwata and coworkers have examined the intramolecular cyclization of an alkyne with a diyne.¹ Their model system is 1, which can cyclize through a concerted transition state TSC togive the benzyne product 2, or it can proceed through a stepwise pathway, first going through TS1 to form the intermediate INT¸ before traversing through a second transition state TS2 and on to product 2. Using both computations and experiments, they examined a series of compounds with
differing substituents at the ends of the two yne moieties.

The experiments show almost the exact same rate of reaction regardless of the terminal substituents. This includes the parent case where the terminal substituents are hydrogens and also the case where the terminal substituents (which end up on adjacent centers on the benzyne ring) are bulky TMS groups. And though there is no real rate effect due to changes in solvent or the presence of light or triplet oxygen, which suggest a concerted reaction, these substituent effects argue for a step wise reaction.

SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p)
computations help explain these observations. Shown in Figure 1 are the optimized geometries and relative energies of the critical points on the reaction surface for the conversion of 1 into 2, and these results are similar with the other substituents as well.

1 (0.0)	2 (-56.9)
TSC (31.5)
TS1 (25.5)	INT (18.8)
TS2 (18.1)

Figure 1. SMD(o-dichlorobenzene)/B3LYP-D3BJ/6-311+G-(d,p)//M06-2X/6-311+G(d,p) optimized geometries and relative energies (kcal mol^-1).

The first thing to note is that the concerted TSC is higher in energy than the stepwise TS1. The wavefunction for TSC unstable towards moving from a restricted to unrestricted formalism. Reoptimization of some of these concerted TSs actually led to the stepwise TS.

The next item of note is that TS2 for this case is actually lower in energy than the intermediate (this is a true TS on the energy surface, but when zero-point energy and other thermal corrections are included, it becomes lower in energy than INT). For some of the cases the second TS lies above the intermediate, but typically by a small amount.

Therefore, the mechanism of this reaction is stepwise, but the second step might have such a small barrier (or even no barrier) that one might consider this to be concerted, though highly asymmetric and really bearing little resemblance to more traditional concerted pericyclic reactions.

The authors obliquely hinted at some potential interesting dynamics. I suspect that molecular dynamics calculations will show no effect of that second TS, and one might observe some interesting dynamics, which could be seen in kinetic isotope experiments.

References

(1)  Marell, D. J.; Furan, L. R.; Woods, B. P.; Lei, X.; Bendelsmith, A. J.; Cramer, C. J.; Hoye, T. R.; Kuwata, K. T. "Mechanism of the Intramolecular Hexadehydro-Diels–Alder Reaction," J. Org. Chem. 2015 ASAP, DOI: 10.1021/acs.joc.5b01356.

InChIs

1: InChI=1S/C8H4O2/c1-3-5-6-7-10-8(9)4-2/h1-2H,7H2
InChIKey=MGXDIFXPYGGQLF-UHFFFAOYSA-N

2: InChI=1S/C8H4O2/c9-8-7-4-2-1-3-6(7)5-10-8/h2,4H,5H2
InChIKey=MYFORDRJCVOBTH-UHFFFAOYSA-N