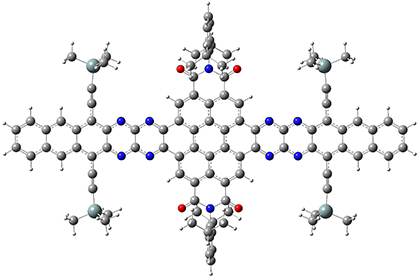
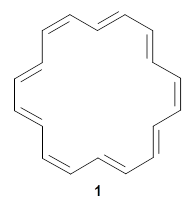
Bunz and co-workers have synthesized the novel aromatic compound 1 that contains 13 acenes in a row.¹

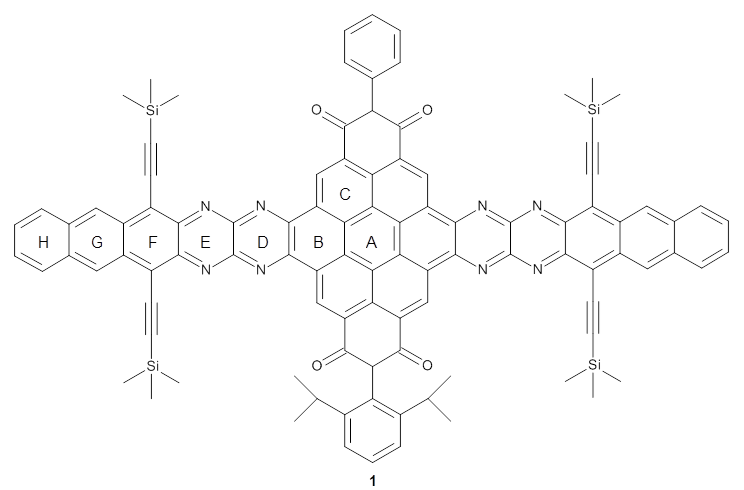
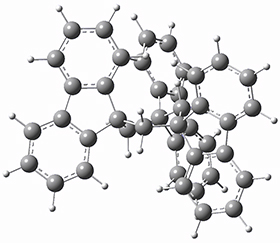
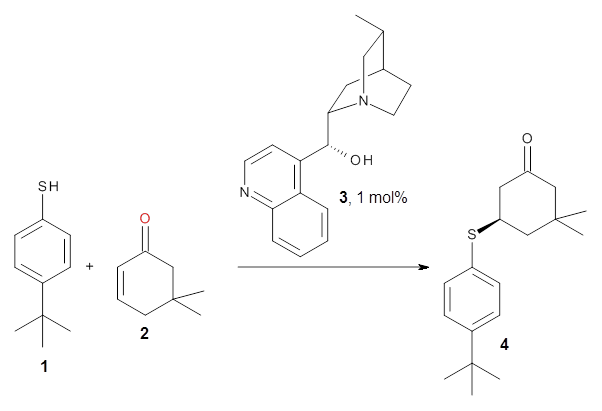
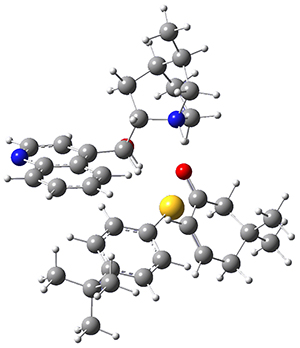
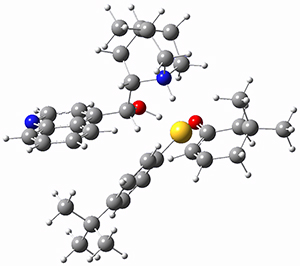
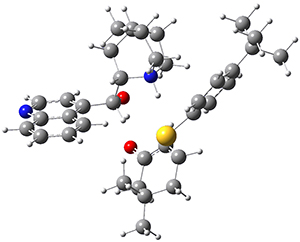
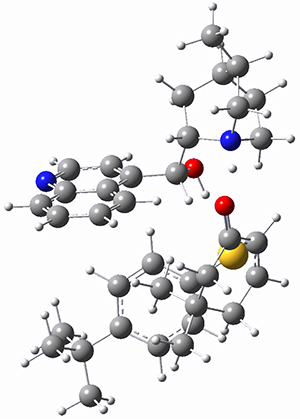
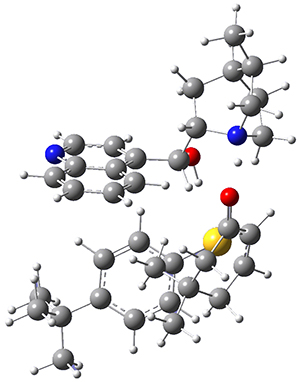
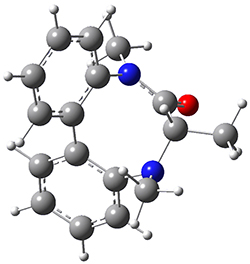
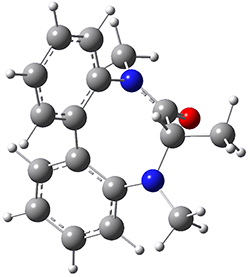
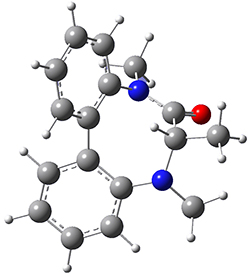
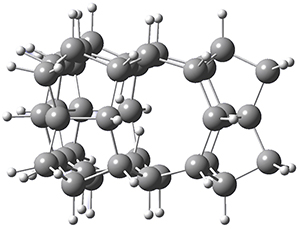
They optimized the geometry of 1 at B3LYP/6-311G*, and its geometry is shown in Figure 1. Even though this compound has quite an extensive π-system, an unrestricted computations collapses to the closed-shell wavefunction.

1

Figure 1. B3LYP/6-311G* optimized geometry of 1. (As always, don’t forget to click on this image to launch JMol and visualize the molecule in 3-D.)

NICS(1)_πzz values for the rings are given in Table 1. Interestingly, the aromaticity of the coronene moiety is reduced; in fact the central ring (ring A, with rings labeled sequentially working towards either end from the center) has a very small NICS value of only -3.77.

Table 1. NICS(1)_πzz values for the rings of 1.

References

(1) Endres, A. H.; Schaffroth, M.; Paulus, F.; Reiss, H.; Wadepohl, H.; Rominger, F.; Krämer, R.; Bunz, U. H. F. "Coronene-Containing N-Heteroarenes: 13 Rings in a Row," J. Am. Chem. Soc. 2016, 138, 1792-1795, DOI: 10.1021/jacs.5b12642.

InChIs

1: InChI=1S/C100H76N8O4Si4/c1-49(2)56-31-24-32-57(50(3)4)75(56)84-95(111)72-47-68-80-78-66(89-91(68)107-99-97(105-89)101-85-58(33-37-113(5,6)7)62-41-52-27-20-22-29-54(52)43-64(62)60(87(85)103-99)35-39-115(11,12)13)45-70-76-71(94(110)74(93(70)109)51-25-18-17-19-26-51)46-67-79(82(76)78)81-69(48-73(96(84)112)77(72)83(80)81)92-90(67)106-98-100(108-92)104-88-61(36-40-116(14,15)16)65-44-55-30-23-21-28-53(55)42-63(65)59(86(88)102-98)34-38-114(8,9)10/h17-32,41-50,74,84H,1-16H3
InChIKey=GNQHLGPUXJMSCH-UHFFFAOYSA-N

Reid, Rathore and colleagues report on the attempted preparation of the interesting molecule 1,3,5-trifluorenylcyclohexane (TFC) 1.¹ They had hoped to prepare it by subjecting the precursor 2 to acid, which might then undergo a Friedel-Crafts reaction to prepare the last fluorenyl group, and subsequent loss of a proton would give 1. Unfortunately, they could not get this step to occur, even at high temperature and for long reaction times. What made it particularly frustrating was that they could get 3 to react under these conditions to give 1,4-difluorenylcyclohexane (14-DFC) 4, and convert 5 into 1,4-difluorenylcyclohexane (13-DFC) 6.

To get at why 1 could not be formed they utilized PCM(CH₂Cl₂)/M06-2X/6-31G(d) calculations. The lowest energy conformations of 1 and 4 are shown in Figure 1. While 4 is in a chair conformation, 1 is not in a chair conformation since this would bring the three fluorenyl groups into very close contact. Instead, the cyclohexyl ring of 1 adopts a twist-boat conformation, with a much flattened ring. They estimate that 1 is strained by about 17 kcal mol^-1, with 10 kcal mol^-1 coming from strain in the twist-boat conformation and another 7 kcal mol^-1 of strain due to steric crowding of the fluorenyl groups.

They next optimized the structures of the intermediates and transition states on the path taking 2 into 1 and 3 into 4. The transition states of the Friedel-Crafts reaction are the highest points on these paths, and their geometries are shown in Figure 1. The barrier through the TS for the Friedel-Crafts step forming 1 is about 17 kcal mol^-1 higher than for the barrier to form 4. This very large increase in activation barrier, due to the strains imposed by that third fluorenyl group, explains the lack of reaction. Furthermore, since the reaction 2 → 1 is 2.0 kcal mol^-1 endothermic, at high temperature the reaction is likely to be reversible and favors 2.

1	4
TS to 1	TS to 4

Figure 1. PCM(CH₂Cl₂)/M06-2X/6-31G(d) optimized geometries.

References

(1) Talipov, M. R.; Abdelwahed, S. H.; Thakur, K.; Reid, S. A.; Rathore, R. "From Wires to Cables: Attempted Synthesis of 1,3,5-Trifluorenylcyclohexane as a Platform for Molecular Cables," J. Org. Chem. 2016, DOI: 10.1021/acs.joc.5b02792.

InChIs

1 (TFC): InChI=1S/C42H30/c1-7-19-34-28(13-1)29-14-2-8-20-35(29)40(34)25-41(36-21-9-3-15-30(36)31-16-4-10-22-37(31)41)27-42(26-40)38-23-11-5-17-32(38)33-18-6-12-24-39(33)42/h1-24H,25-27H2
InChIKey=CXXRVQFQMRJLAI-UHFFFAOYSA-N

4 (14-DFC): InChI=1S/C30H24/c1-5-13-25-21(9-1)22-10-2-6-14-26(22)29(25)17-19-30(20-18-29)27-15-7-3-11-23(27)24-12-4-8-16-28(24)30/h1-16H,17-20H2
InChIkey=ZZTDGVHNROVFMK-UHFFFAOYSA-N

6 (13-DFC):InChI=1S/C30H24/c1-2-11-22(12-3-1)24-14-4-5-15-25(24)23-13-10-20-30(21-23)28-18-8-6-16-26(28)27-17-7-9-19-29(27)30/h1-9,11-19H,10,20-21H2
InChIKey=TTZIUDUAWUTKAI-UHFFFAOYSA-N

The ACS National Meeting this week in San Diego had computers in chemistry as its theme. A number of sessions featured computer-aided drug design, and the paper that garnered a lot of attention in many of these sessions was one I missed from last year. The work, done by the Schrödinger company, presents the application of some improved techniques for performing free energy perturbation (FEP) computations.¹ FEP involves changing a small number of atoms from one type to another and determining the free energy change with this perturbation. Since so much of the system is left unaffected, the idea is that errors in the non-perturbed parts of the system will cancel, allowing for accurate determination of the free energy change due to the perturbation.

This study features a number of new technologies that have enabled much more accurate predictions. First, they have employed a new force field, OPLS2.1, which appears to provide much improved energies. Second, they have improved sampling of configuration space using the Desmond program and replica exchange with solute tempering (REST). Third, these have been implemented on GPUs that results in dramatically improved throughput. And fourth, they developed a workflow to automate the selection of ligands, created by the perturbations with the protein of interest. They examined up to 10 atom perturbations within the initial ligand.

In a validation study of 8 proteins involving 330 ligands, the RMS error in the free energy of binding was about 1 kcal mol^-1. Case studies of different types of perturbations leading to gain or loss of hydrophobic or electrostatic interactions, loss of a binding water and exposure to solvent are detailed. Lastly, in a study of two new proteins, they report a high success in predicting both strong binders and weak binders, with very few false positives.

References

(1) Wang, L.; Wu, Y.; Deng, Y.; Kim, B.; Pierce, L.; Krilov, G.; Lupyan, D.; Robinson, S.; Dahlgren, M. K.; Greenwood, J.; Romero, D. L.; Masse, C.; Knight, J. L.; Steinbrecher, T.; Beuming, T.; Damm, W.; Harder, E.; Sherman, W.; Brewer, M.; Wester, R.; Murcko, M.; Frye, L.; Farid, R.; Lin, T.; Mobley, D. L.; Jorgensen, W. L.; Berne, B. J.; Friesner, R. A.; Abel, R. "Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field," J. Am. Chem. Soc. 2015, 137, 2695-2703, DOI: 10.1021/ja512751q.

Cinchona alkaloids cat catalyze reactions, such as shown in Reaction 1. Wynberg¹ proposed a model to explain the reaction, shown in Scheme 1, based on NMR. Grayson and Houk have now used DFT computations to show that the mechanism actually reverses the arrangements of the substrates.²

Reaction 1

Scheme 1.

M06-2X/def2-TZVPP−IEFPCM(benzene)//M06-2X/6-31G(d)−IEFPCM(benzene) computations show that the precomplex of catalyst 3 with nucleophile 1 and Michael acceptor 2 is consistent with Wynberg’s model. The alternate precomplex is 5.6 kcal mol^-1 higher in energy. These precomplexes are shown in Figure 1.

Wynberg precomplex

Grayson/Houk precomplex

Figure 1. Precomplexes structures

However, the lowest energy transition state takes the Grayson/Houk pathway and leads to the major isomer observed in the reaction. The Grayson/Houk TS that leads to the minor product has a barrier that is 3 kcal mol^-1 higher in energy. The lowest energy TS following the Wynberg path leads to the minor product, and is 2.2 kcal mol^-1 higher than the Grayson/Houk path. These transition states are shown in Figure 2. The upshot is that complex formation is not necessarily indicative of the transition state structure.

Wynberg TS (major) Rel ΔG = 5.3	Wynberg TS (minor) Rel ΔG = 2.2
Grayson/Houk TS (major) Rel ΔG = 0.0	Grayson/Houk TS (minor) Rel ΔG = 3.0

Figure 2. TS structures and relative free energies (kcal mol^-1).

References

(1) Hiemstra, H.; Wynberg, H. "Addition of aromatic thiols to conjugated cycloalkenones, catalyzed by chiral .beta.-hydroxy amines. A mechanistic study of homogeneous catalytic asymmetric synthesis," J. Am. Chem. Soc. 1981, 103, 417-430, DOI: 10.1021/ja00392a029.

(2) Grayson, M. N.; Houk, K. N. "Cinchona Alkaloid-Catalyzed Asymmetric Conjugate Additions: The Bifunctional Brønsted Acid–Hydrogen Bonding Model," J. Am. Chem. Soc. 2016, 138, 1170-1173, DOI: 10.1021/jacs.5b13275.

InChIs

1: InChI=1S/C10H14S/c1-10(2,3)8-4-6-9(11)7-5-8/h4-7,11H,1-3H3
InChIKey=GNXBFFHXJDZGEK-UHFFFAOYSA-N

2: InChI=1S/C8H12O/c1-8(2)5-3-4-7(9)6-8/h3-4H,5-6H2,1-2H3
InChIKey=CDDGRARTNILYAB-UHFFFAOYSA-N

3: InChI=1S/C18H22N2O/c1-12-11-20-9-7-13(12)10-17(20)18(21)15-6-8-19-16-5-3-2-4-14(15)16/h2-6,8,12-13,17-18,21H,7,9-11H2,1H3/t12?,13?,17?,18-/m1/s1
InChIKey=ZOZLJWFJLBUKKL-NKHWWFDVSA-N

4: InChI=1S/C18H26OS/c1-17(2,3)13-6-8-15(9-7-13)20-16-10-14(19)11-18(4,5)12-16/h6-9,16H,10-12H2,1-5H3/t16-/m0/s1
InChIKey=XUTYYZOSKLYWLW-INIZCTEOSA-N

What is the size of a molecule that will stretch computational resources today? Chan and co-workers have examined some very large fullerenes¹ to both answer that question, and also to explore how large a fullerene must be to approach graphene-like properties.

They are interested in predicting the heat of formation of large fullerenes. So, they benchmark the heats of formation of C₆₀ using four different isodesmic reactions (Reaction 1-4), comparing the energies obtained using a variety of different methods and basis sets to those obtained at W1h. The methods include traditional functionals like B3LYP, B3PW91, CAM-B3LYP, PBE1PBE, TPSSh, B98, ωB97X, M06-2X3, and MN12-SX, and supplement them with the D3 dispersion correction. Additionally a number of doubly hybrid methods are tested (again with and without dispersion corrections), such as B2-PLYP, B2GPPLYP, B2K-PLYP, PWP-B95, DSD-PBEPBE, and DSD-B-P86. The cc-pVTZ and cc-pVQZ basis sets were used. Geometries were optimized at B3LYP/6-31G(2df,p).

Excellent results were obtained with DSD-PBEPBE-D3/cc-pVQZ (an error of only 1.8 kJ/mol), though even a method like BMK-D3/cc-pVTZ had an error of only 9.2 kJ/mol. They next set out to examine large fullerenes, including such behemoths as C₁₈₀, C₂₄₀, and C₃₂₀, whose geometries are shown in Figure 1. Heats of formation were obtained using isodesmic reactions that compare back to smaller fullerenes, such as in Reaction 5-8.

C180

C240

C320

Figure 1. B3LYP/6-31G(2df,p) optimized geometries of C₁₈₀, C₂₄₀, and C₃₂₀. (Don’t forget that clicking on these images will launch Jmol and allow you to manipulate the molecules in real-time.)

Next, taking the heat of formation per C for these fullerenes, using a power law relationship, they were able to extrapolate out the heat of formation per C for truly huge fullerenes, and find the truly massive fullerenes, like C₉₆₈₀, still have heats of formation per carbon 1 kJ/mol greater than for graphene itself.

References

(1) Chan, B.; Kawashima, Y.; Katouda, M.; Nakajima, T.; Hirao, K. "From C₆₀ to Infinity: Large-Scale Quantum Chemistry Calculations of the Heats of Formation of Higher Fullerenes," J. Am. Chem. Soc. 2016, 138, 1420-1429, DOI: 10.1021/jacs.5b12518.

Atropisomers are stereoisomer that differ by axial symmetry, such as in substituted biphenyls or allenes. These acyclic systems have received a fair amount of attention, but now Buevich has looked at atropisomerization that occurs in a ring system.¹ 1 has a biphenyl as part of the eight-member ring, and the biphenyl can exist in either an M or P orientation. Since C3 is chiral (S), the two isomers are (M,S)-1 and (P,S)-1. Variable temperature NMR analysis concludes that (P,S)-1 is 1.19 kcal mol^-1 more stable than (M,S)-1, and the barrier for the interchange (P,S)-1 → (M,S)-1 is 26.77 kcal mol^-1.

To identify the process for this atropisomerization process, he utilized B3LYP/6-31G(d) computations of the model system 2. A variety of different techniques were used to identify the local energy minimum conformations of both (M,S)-2 and (P,S)-2, and the lowest energy conformers (M1 for (P,S)-2 and M4 for (M,S)-2) are shown in Figure 1. He then produced a series of 2-D potential energy surfaces varying two of the dihedral angles defining the eight-member ring to help identify potential initial geometries for searching for transition states. (As an aside, this procedure ended up identifying a few additional local energy minima not identified in the initial conformational search – and these all have trans amide groups instead of the cis relationship found initially. These trans isomer are considerably higher in energy than the conformers.) With this model and this computational level, (P,S)-2 is 0.76 kcal mol^-1 lower in energy than (M,S)-2.

M1 0.0	TS1 3.54
M2 2.21	TS4 25.83
M4 0.76

Table 1. B3LYP/6-31G(d) optimized geometries and relative free energies of some critical points along the lowest energy pathway taking (P,S)-2 → (M,S)-2.

A number of transition states were identified, and the lowest energy pathway that takes M1 into M4 first crosses TS1 to make the minimum M2, which than passes a high barrier (25.8 kcal mol^-1) to go to M4. This barrier is in reasonable agreement with the experimental barrier for 1. These TSs are also shown in Figure 1.

Buevich analyzes the conformational process by examination of the changes in the ring dihedral angles following this reaction path. As expected, crossing the highest barrier requires a combination of torsional rotations, but essentially one at a time moving clockwise about the ring.

References

(1) Buevich, A. V. "Atropisomerization of 8-Membered Dibenzolactam: Experimental NMR and Theoretical DFT Study," J. Org. Chem. 2016, 81, 485–501 DOI: 10.1021/acs.joc.5b02321.

InChIs

1: InChI=1S/C27H26N2O/c1-3-12-26-27(30)29(20-21-13-6-5-7-14-21)25-18-11-9-16-23(25)22-15-8-10-17-24(22)28(26)19-4-2/h3-11,13-18,26H,1-2,12,19-20H2/t26-/m0/s1
InChIKey=IYYACMIVKDJSJD-SANMLTNESA-N

2: InChI=1S/C17H18N2O/c1-12-17(20)19(3)16-11-7-5-9-14(16)13-8-4-6-10-15(13)18(12)2/h4-12H,1-3H3/t12-/m0/s1
InChIKey=NIBPKKMKNFOPRM-LBPRGKRZSA-N

I discuss the aqueous Diels-Alder reaction in Chapter 7.1 of my book. A key case is the reaction of methyl vinyl ketone with cyclopentadiene, Reaction 1. The reaction is accelerated by a factor of 740 in water over the rate in isooctane.¹ Jorgensen argues that this acceleration is due to stronger hydrogen bonding to the ketone than in the transition state than in the reactants.^2-4

Doubleday and Houk⁵ report a procedure for calculating trajectories including explicit water as the solvent and apply it to Reaction 1. Their process is as follows:

1. Compute the endo TS at M06-2X/6-31G(d) with a continuum solvent.
2. Equilibrate water for 200ps, defined by the TIP3P model, in a periodic box, with the transition state frozen.
3. Continue the equilibration as in Step 2, and save the coordinates of the water molecules after every addition 5 ps, for a total of typically 25 steps.
4. For each of these solvent configurations, perform an ONIOM computation, keeping the waters fixed and finding a new optimum TS. Call these solvent-perturbed transition states (SPTS).
5. Generate about 10 initial conditions using quasiclassical TS mode sampling for each SPTS.
6. Now for each the initial conditions for each of these SPTSs, run the trajectories in the forward and backward directions, typically about 10 of them, using ONIOM to compute energies and gradients.
7. A few SPTS are also selected and water molecules that are either directly hydrogen bonded to the ketone, or one neighbor away are also included in the QM portion of the ONIOM, and trajectories computed for these select sets.

The trajectory computations confirm the role of hydrogen bonding in stabilizing the TS preferentially over the reactants. Additionally, the trajectories show an increasing asynchronous reactions as the number of explicit water molecules are included in the QM part of the calculation. Despite an increasing time gap between the formation of the first and second C-C bonds, the overwhelming majority of the trajectories indicate a concerted reaction.

References

(1) Breslow, R.; Guo, T. "Diels-Alder reactions in nonaqueous polar solvents. Kinetic
effects of chaotropic and antichaotropic agents and of β-cyclodextrin," J. Am. Chem. Soc. 1988, 110, 5613-5617, DOI: 10.1021/ja00225a003.

(2) Blake, J. F.; Lim, D.; Jorgensen, W. L. "Enhanced Hydrogen Bonding of Water to Diels-Alder Transition States. Ab Initio Evidence," J. Org. Chem. 1994, 59, 803-805, DOI: 10.1021/jo00083a021.

(3) Chandrasekhar, J.; Shariffskul, S.; Jorgensen, W. L. "QM/MM Simulations for Diels-Alder
Reactions in Water: Contribution of Enhanced Hydrogen Bonding at the Transition State to the Solvent Effect," J. Phys. Chem. B 2002, 106, 8078-8085, DOI: 10.1021/jp020326p.

(4) Acevedo, O.; Jorgensen, W. L. "Understanding Rate Accelerations for Diels−Alder Reactions in Solution Using Enhanced QM/MM Methodology," J. Chem. Theor. Comput. 2007, 3, 1412-1419, DOI: 10.1021/ct700078b.

(5) Yang, Z.; Doubleday, C.; Houk, K. N. "QM/MM Protocol for Direct Molecular Dynamics of Chemical Reactions in Solution: The Water-Accelerated Diels–Alder Reaction," J. Chem. Theor. Comput. 2015, , 5606-5612, DOI: 10.1021/acs.jctc.5b01029.

Setting the record for the shortest non-bonded H^…H contact has become an active contest. Following on the report of a contact distance of only 1.47 Å that I blogged about here, Firouzi and Shahbazian propose a series of related cage molecules with C-H bonds pointed into their interior.¹ The compounds were optimized with a variety of computational methods, and many of them have H^…H distances well below that of the previous record. The shortest distance is found in 1, shown in Figure 1. The H^…H distance in 1 is predicted to be less than 1.2 Å with a variety of density functionals and moderate basis sets.

1

Figure 1. Optimized geometry of 1 at ωB97X-D/cc-pVDZ.

References

(1) Firouzi, R.; Shahbazian, S. "Seeking Extremes in Molecular Design: To What Extent May Two “Non-Bonded” Hydrogen Atoms be Squeezed in a Hydrocarbon?," ChemPhysChem 2016, 17, 51-54, DOI: 10.1002/cphc.201501002.

InChIs

1: InChI=1S/C41H44/c1-7-13-25-17-9-3-40-5-11-19(35(17)40)27-15-8-2-39(1,33(13)15)34-14(7)26-18-10-4-41-6-12-20(36(18)41)28(16(8)34)32(27)30-23(11)37(40)21(9)29(31(25)26)22(10)38(41)24(12)30/h7-38H,1-6H2
InChIKey=DMWSEJFKSWCSLI-UHFFFAOYSA-N

Assessing when a molecular system might be subject to sizable static (non-dynamic) electron correlation, necessitating a multi-reference quantum mechanical treatment, is perhaps more art than science. In general one suspects that static correlation will be important when the frontier MO energy gap is small, but is there a way to get more guidance?

Grimme reports the use of fractional occupancy density (FOD) as a visualization tool to identify regions within molecules that demonstrate significant static electron correlation.¹ The method is based on the use of finite temperature DFT.^2,3

The resulting plots of the FOD for a series of test cases follow our notions of static correlation. Molecules, such as alkanes, simple aromatics, and concerted transition states show essentially no fractional orbital density. On the other hand, the FOD plot for ozone shows significant density spread over the entire molecule; the transition state for the cleavage of the terminal C-C bond in octane shows FOD at C₁ and C₂ but not elsewhere; p-benzyne shows significant FOD at the two radical carbons, while the FOD is much smaller in m-benzyne and is negligible in o-benzyne.

This FOD method looks to be a simple tool for evaluating static correlation and is worth further testing.

References

(1) Grimme, S.; Hansen, A. "A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects," Angew. Chem. Int. Ed. 2015, 54, 12308-12313, DOI: 10.1002/anie.201501887.

(2) Mermin, N. D. "Thermal Properties of the Inhomogeneous Electron Gas," Phys. Rev. 1965, 137, A1441-A1443, DOI: 10.1103/PhysRev.137.A1441.

(3) Chai, J.-D. "Density functional theory with fractional orbital occupations," J. Chem. Phys 2012, 136, 154104, DOI: doi: 10.1063/1.3703894.

The prediction of NMR chemical shifts and coupling constants through ab initio computation is a major development of the past decade in computational organic chemistry. I have written about many developments on this blog. An oft-used method is a linear scaling of the computed chemical shifts to match those of some test set. Kwan and Liu wondered if the dynamics of molecular motions might be why we need this correction.¹

They suggest that the chemical shift can be computed as

<σ> = σ(static molecule using high level computation) + error

where the error is the obtained by using a low level computation taking the difference between the chemical shifts obtained on a dynamic molecule less that obtained with a static molecule. The dynamic system is obtained by performing molecular dynamics of the molecule, following 25 trajectories and sampling every eighth point.

They find outstanding agreement for the proton chemical shift of 12 simple molecules (mean error of 0.02 ppm) and the carbon chemical shift of 19 simple molecules (mean error of 0.5 ppm) without any scaling. Similar excellent agreement is found for a test set of natural products.

They finish up with a discussion of [18]annulene 1. The structure of 1 is controversial. X-ray crystallography indicates a near D_6h geometry, but the computed NMR shifts using a D_6h geometry are in dramatic disagreement with the experimental values, leading Schleyer to suggest a C₂  geometry. Kwan and Liu applied their dynamic NMR method to the D_6h, D_3h, and C₂ structures, and find the best agreement with the experimental chemical shifts are from the dynamic NMR initiated from the D_6h geometry. Dynamic effects thus make up for the gross error found with the static geometry, and now bring the experimental and computational data into accord.

One final note on this paper. The authors indicate that they have filed a provisional patent on their method. I am disturbed by this concept of patenting a computational methodology, especially in light of the fact that many other methods have been made available to the world without any legal restriction. For example, full details including scripts to apply Tantillo’s correction method are available through the Cheshire site and a web app to implement Goodman’s DP4 method are available for free. Provisional patents are not available for review from the US Patent Office so I cannot assess just what is being protected here. However, I believe that this action poses a real concern over the free and ready exchange of computational methodologies and ideas.

References

(1) Kwan, E. E.; Liu, R. Y. "Enhancing NMR Prediction for Organic Compounds Using Molecular Dynamics," J. Chem. Theor. Comput. 2015, 11, 5083-5089, DOI: 10.1021/acs.jctc.5b00856.

InChIs

1: InChI=1S/C18H18/c1-2-4-6-8-10-12-14-16-18-17-15-13-11-9-7-5-3-1/h1-18H/b2-1-,3-1+,4-2+,5-3+,6-4+,7-5-,8-6-,9-7+,10-8+,11-9+,12-10+,13-11-,14-12-,15-13+,16-14+,17-15+,18-16+,18-17-
InChIKey=STQWAGYDANTDNA-DWSNDWDZSA-N