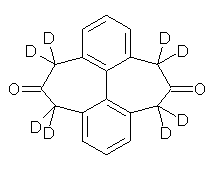
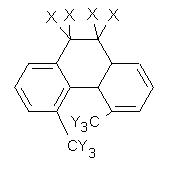
Kinetic isotope effects (KIE) are a valuable tool for probing mechanisms without changing the potential energy surface. Their interpretation can sometimes be difficult – for example is a perdeutero group larger or smaller than the perhydro analogue?

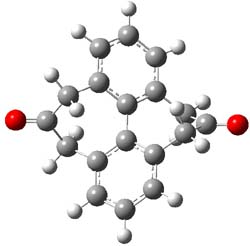
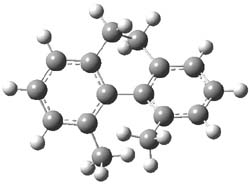
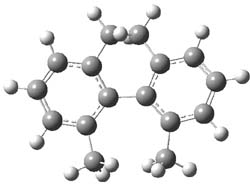
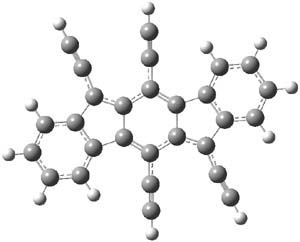
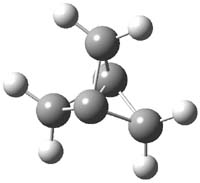
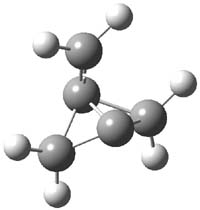
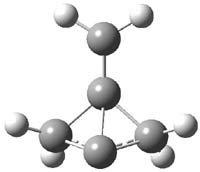
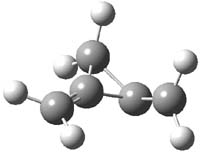
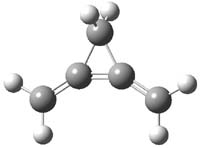
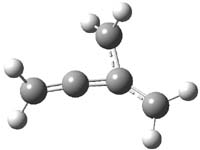
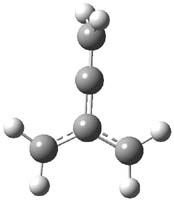
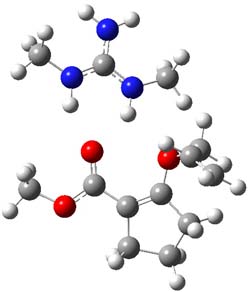
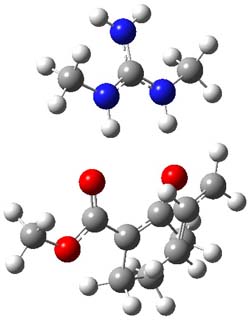
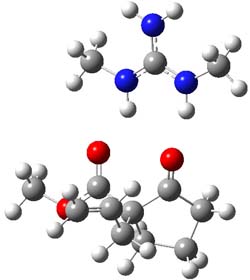
O’Leary, Rablen and Meyer have examined two related molecules and their KIEs relating to stereoinversion.¹ 1 exhibits a normal isotope effect (k_H/k_D = 1.06) while 2 has an inverse isotope effect (k_H/k_D = 0.880). They optimized the structures and transition states (see Figure 1) for racemization of both compounds at B3LYP and MP2, and computed isotope effects based on the Biegeleisen-Mayer equation (which is based on reduced partition functions). The KIEs obtained from the two computational methods is very similar.

1	1TS
2	2TS

Figure 1. MP2/6-31G(d,p) optimized geometries of 1 and 2 and the transition states for their racemization.

The experimental and computed KIEs are listed in Table 1. The agreement between experiment and computation is excellent – suggesting that computations should be routinely employed when analyzing isotope effects.

Table 1. Experimental and computed KIEs for racemization of 1 and 2.

The authors decompose the isotope effects into enthalpic and entropic components and note that the interplay between these two can be subtle – sometimes one might dominate and other times the second term will dominate, and the terms can be cooperative or non-cooperative.

References

(1) O’Leary, D. J.; Rablen, P. R.; Meyer, M. P., "On the Origin of Conformational Kinetic Isotope Effects," Angew. Chem. Int. Ed., 2011, 50, 2564-2567, DOI: 10.1002/anie.201007322

InChIs

1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2
InChIKey=DYZSIUYFWKNLHS-UHFFFAOYAB

d₈–1: InChI=1/C18H14O2/c19-15-7-11-3-1-4-12-8-16(20)10-14-6-2-5-13(9-15)18(14)17(11)12/h1-6H,7-10H2/i7D2,8D2,9D2,10D2
InChIKey=DYZSIUYFWKNLHS-UFBJYANTEO

2: InChI=1/C16H18/c1-11-5-3-7-13-9-10-14-8-4-6-12(2)16(14)15(11)13/h3-8,13,15H,9-10H2,1-2H3
InChIKey=OBRIKDRTDGHGIQ-UHFFFAOYAU

The search for ever more intriguing aromatic/antiaromatic species continues on – Haley has recently prepared the TIPS-protected indeno[1,2-b]fluorene 1. ¹ The crystal structure was determined and analogue with the tri-iso-propylsilyl groups replaced with hydrogens (2) has been computed at B3LYP/6-31G(d,p). This optimized structure is shown in Figure 1. The core system has 20 π-electrons – suggesting perhaps an antiaromatic system.

1

2

Figure 1. B3LYP/6-31G(d,p) optimized geometry of 2.

The x-ray structure and computed structure are in close agreement in terms of distances. The terminal phenyl rings exhibit very little alternation. The C₁-C₂ and C₂-C₃ distances are long (1.444 and 1.457 Å, respectively) while the C₁-C_3A and C­2-C₄ distances are short (1.379 and 1.396 Å, respectively.) This suggests a para-xylylene type structure for the central six-member ring. The NICS values of the terminal 6-member ring, the 5-member ring and the central 6-member ring are computed to be -7.12 (a reasonable phenyl value), 1.84, and 0.02. So the middle three rings possess no aromatic or antiaromatic character. Haley describes this structure as “a fully conjugated 20-π-electron hydrocarbon with fused s-trans 1,3-diene linkages across the top and bottom portions of the carbon skeleton”.

References

(1) Chase, D. T.; Rose, B. D.; McClintock, S. P.; Zakharov, L. N.; Haley, M. M., "Indeno[1,2-b]fluorenes: Fully Conjugated Antiaromatic Analogues of Acenes," Angew. Chem. Int. Ed., 2011, 50, 1127-1130, DOI: 10.1002/anie.201006312

InChIs

1: InChI=1/C64H92Si4/c1-41(2)65(42(3)4,43(5)6)37-33-57-53-29-25-27-31-55(53)61-60(36-40-68(50(19)20,51(21)22)52(23)24)64-58(34-38-66(44(7)8,45(9)10)46(11)12)54-30-26-28-32-56(54)62(64)59(63(57)61)35-39-67(47(13)14,48(15)16)49(17)18/h25-32,41-52H,1-24H3
InChIKey=JIXLLIXVMPJPEE-UHFFFAOYAI

2: InChI=1/C28H12/c1-5-17-21-13-9-11-15-23(21)27-20(8-4)26-18(6-2)22-14-10-12-16-24(22)28(26)19(7-3)25(17)27/h1-4,9-16H
InChIKey=DOQPHDKEGVECBF-UHFFFAOYAY

Proper handling of hydrogen bonding using DFT remains a concern. Sherrill has reported a careful benchmark study using the potential energy curves for the six dimer combinations involving formic acid, formamide, and formamidine.¹ Comparisons are made to the the CBS extrapolated limit CCSD(T) curve.

As anticipated, B3LYP and related functionals do a poor job. Interestingly, PBE and PBE0 provide very nice curves. The meta-GGA functionals like M05-2x and M06-2x and functionals with dispersion corrections (like ωB97X-D) provide very good potential energy curves. It is clear that intermediate and long-range correlation and dispersion must be accounted for when handling hydrogen bonded systems. Proper selection of the functional is critical.

References

(1) Thanthiriwatte, K. S.; Hohenstein, E. G.; Burns, L. A.; Sherrill, C. D., “Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions,” J. Chem. Theory Comput., 2011, 7, 88-96, DOI: 10.1021/ct100469b.

Palau’amine has been of interest since its discovery in the early 1990s. It was just recently synthesized by Baran,¹ to much acclaim. The structure of palau’amine underwent numerous revisions, and though the relative configuration had been settled, the absolute configuration was only determined by Reinscheid and Griesinger using a combination of experimental and computed ECD and ORD spectra.²

3,4-dibromopalau’amine 1 was subjected to careful NMR analysis to set as much of the overall structure as possible. Then two conformations were optimized at B3LYP/6-31G(d), one of which is displayed in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized structure of 1.

TD-DFT computations including PCM gave an ECD spectrum that nicely matches with experiment, especially where the positive and negative peaks occur. The computed and experimental ORD spectra also match well, with all the signs matching up and a difference in the absolute value of the rotation of no more that 25%. The resulting absolute configuration is (-)-(6S,10R,11S,12S,16R,17S,18S,20S)-dibromopalau’amine, demonstrating again the power of combining computation and experiment for structure determination!

References

(1) Seiple, I. B.; Su, S.; Young, I. S.; Lewis, C. A.; Yamaguchi, J.; Baran, P. S., "Total Synthesis of Palau’amine," Angew. Chem. Int. Ed., 2010, 49, 1095-1098, DOI: 10.1002/anie.200907112

(2) Reinscheid, U. M.; Köck, M.; Cychon, C.; Schmidts, V.; Thiele, C. M.; Griesinger, C., "The Absolute Configuration of Dibromopalau’amine," Eur. J. Org. Chem., 2010, 6900-6903, DOI: 10.1002/ejoc.201001392

InChI

1: InChI=1/C17H22Br2ClN9O2/c18-6-1-7-11(30)28-3-5-4(2-21)9(20)16(13(31)25-15(23)26-16)8(5)17(28)12(24-14(22)27-17)29(7)10(6)19/h1,4-5,8-9,12-13,24-27,31H,2-3,21-23H2/q+2/p+1/t4-,5-,8+,9+,12+,13+,16+,17-/m1/s1/fC17H23Br2ClN9O2/h21H/q+3
InChIKey=VGQTUXLYZXIYTJ-CAGSSHLPDN

1,2-Azaborine appears to be aromatic (see my previous post). Can the extent of aromatic character be measured? Well, obviously the first thing one must decide is just which “aromaticity metric” to choose. Dixon and Liu have now measured the aromatic resonance stablilization energy (ASE) through computations and heats of hydrogenation.¹

One can set up to hydrogenation comparisons. First, obtain the hydrogenation of 1,2-azaborine itself. They used the t-butyl analog 1, so the hydrogenation is given in Reaction 1.

Then as comparison, one can perform two separate hydrogenations, looking at the double bond adjacent to the nitrogen (Reaction 2) and the double bond adjacent to the boron (Reaction 3).

The heat of hydrogenation of Reaction 1 is -30 ± 1 kcal mol^-1 (-30.1 at G3(MP2). The heats of hydrogenations of reactions 2 and 3 are -22.7 ± 0.5 kcal mol^-1 (-23.8) and -23.9 ± 0.7 (-24.7), respectively. The difference between the sum of reactions 2 and 3 and Reaction 1 is the ASE: 16.6 kcal mol^-1 (18.4 at G3(MP2)). This can be compared to the ASE of benzene determined in the analogous way to be 32.4 kcal mol^-1. Therefore, 1,2-azoborine is aromatic, but appreciably less so than benzene, which is consistent with the NICS computations (see the post).

References

(1) Campbell, P. G.; Abbey, E. R.; Neiner, D.; Grant, D. J.; Dixon, D. A.; Liu, S.-Y., "Resonance Stabilization Energy of 1,2-Azaborines: A Quantitative Experimental Study by Reaction Calorimetry," J. Am. Chem. Soc., 2010, 132, 18048-18050, DOI: 10.1021/ja109596m

The structure of organic molecules of biochemical significance remains an important pursuit, one that I have discussed in a number of blog posts. Highlighted particularly in this blog (and in my book) has been the interplay of experiment and computation in structure determination. Dopfer and co-workers combine IR multiple photon dissociation (IRMPD) with DFT and MP2 computations to determine the structure of protonated serotonin 1H+.¹

B3LYP/cc-pVDZ and MP2/cc-pVDZ computations of the conformations of 1H+ give nearly identical results. The lowest energy conformer (see Figure 1) has the ethylamine group in a gauche arrangement so that the protonated amine can interact with the π-system of the ring. The hydroxyl group is orientated trans relative to the ethylamine group. Conformer generated by rotation about the C-O bond or the C-C and C-N bond of the ethylamine group are higher in energy, anywhere from 0.5 to about 5 kcal mol^-1 above the lowest conformer. Protonation at the ring nitrogen or the oxygen are more than 20 kcal mol^-1 higher in energy than the lowest conformer.

1H+

Figure 1. B3LYP/6-31G(d) optimized geometry of 1H+. Note that the authors did not supply sufficient information in their supporting materials to generate the full 3-D coordinates of the molecule, and I did not want to reoptimize at cc-pVDZ. Referees – please insist on complete supporting information!

Comparison of the experimental IR spectrum of 1H+ with the computed IR frequencies (either B3LYP or MP2 – they are very similar) reveals a remarkable agreement with the computed spectra of just the lowest energy conformer. While the lowest energy conformer is predicted to be nearly 70% of the population, there is little spectroscopic evidence of the participation of any other conformer. In fact, the next three lowest energy conformers have a distinctive peak (in their computed IR spectrum) at about 1400 cm^-1, a region that has virtually no absorption in the experimental IR.

References

(1) Lagutschenkov, A.; Langer, J.; Berden, G.; Oomens, J.; Dopfer, O., "Infrared Spectra of Protonated Neurotransmitters: Serotonin," J. Phys. Chem. A, 2010, 114, 13268-13276, DOI: 10.1021/jp109337a

InChIs

serotonin: InChI=1/C10H12N2O/c11-4-3-7-6-12-10-2-1-8(13)5-9(7)10/h1-2,5-6,12-13H,3-4,11H2
InChIKey=QZAYGJVTTNCVMB-UHFFFAOYAX

1H+: InChI=1/C10H12N2O/c11-4-3-7-6-12-10-2-1-8(13)5-9(7)10/h1-2,5-6,12-13H,3-4,11H2/p+1/fC10H13N2O/h11H/q+1
InChIKey=QZAYGJVTTNCVMB-HISXSYJOCA

This one is a bit afield from organic chemistry, but the result is important for computational chemists who are interested in electron density analysis.

The topological electron density analysis of Bader (also called Atoms-In-Molecules – AIM) carves up a molecular electron density into regions associated with an attractor. The attractor is a critical point in the electron density that is a maximum in all directions. Gradient paths, paths that trace increasing electron density, terminate at such an attractor. The union of all such paths defines a basin. Bader found that for typical molecules, the attractor is coincident with the position of the atomic nucleus. He has then assumed a 1:1 correspondence between these two – all nuclei are attractors and all attractors correspond with nuclei.

This correspondence has been questioned in computations on some metals. For example, Li_n and Na_n (n=2,4,6) have a non-nuclear attractor. However, no clear-cut unambiguous experimental observation of non-nuclear attractors has been made, until now. Platts and Stasch¹ have obtained the x-ray diffraction electron density of 1 and they find a non-nuclear attractor near the midpoint of the Mg-Mg bond. This is corroborated by DFT computations of 1 and some related systems. It should be said that the electron density along the Mg-Mg path is quite flat in the middle, but the attractor is present, and the integrated number of electrons within the basin associated with this non-nuclear attractor is a non-trivial 0.81 e (experiment) or 0.79 e (DFT).

It now appears incontrovertible that non-nuclear attractors of the molecular electron density can exist. It would be especially interesting if these types of points could be located in organic species.

References

(1) Platts, J. A.; Overgaard, J.; Jones, C.; Iversen, B. B.; Stasch, A., "First Experimental Characterization of a Non-nuclear Attractor in a Dimeric Magnesium(I) Compound," J. Phys. Chem. A, 2011, 115, 194-200, DOI: 10.1021/jp109547w

Here’s a real tour de force study combining exciting experiments with detailed computations. It’s a look at the radical cation of propellane performed by Bally and Williams.¹ This paper has been nicely reviewed by Hiberty.²

Propellane 1, whose bridgehead-bridgehead bond has been a topic of an earlier post, has a HOMO that is largely outside of the bridgehead-bridgehead region. Thus, loss of an electron to form the radical cation 1^.+ seems unlikely to lead to any significant geometrical change. However, the ESR of the radical cation of propellane shows two types of hydrogens, one type of four hydrogens and a second type of two hydrogens. This is incompatible with a D_3h structure similar to that of 1. Furthermore, loss of an electron from dimethylenecyclopropane 2 leads to a species whose ESR is nearly identical to that of the radical cation of propellane. Analysis of the ESR suggests that the radical actually produced is 3^.+.

CCSD(T)/cc-pVTZ//B3LYP/6-31G* computations were performed to try to discern a mechanism for this rearrangement. The D_3h structure of 1^.+ is a local energy minimum with most computational methods, though not with B3LYP, where it is a TS connecting mirror image C₂ structures. Breaking symmetry to C₂ leads to a TS (TS1) for cleaving one of the C-C_bridgehead bonds. This TS is only 1.15 kcal mol^-1 above 1^.+, and leads to 4^.+, 7.38 kcal mol^-1 below 1^.+. Cleavage of a second C-C_bridgehead bond passes through TS2, with a barrier from 4^.+ of only 2.89 kcal mol^-1. This leads to 2^.+. Lastly, cleavage of a third C-C_bridgehead bond through TS3, with a barrier of only 2.09 kcal mol^-1 above 2^.+, leads to 3^.+, overall 30.4 kcal mol^-1 exothermic from 1^.+. The structures of these critical points are shown in Figure 1. Quite a neat little pathway – three sequential bond ruptures without ever cleaving what was the weakest bond in the original compound (the bridgehead-bridgehead bond)!

1.+ 0.0	TS1 +1.15
4.+ -7.38	TS2 -4.49
2.+ -24.54	TS3 -22.45
3.+ -30.41

Table 1. B3LYP/6-31G* optimized critical points on the pathway of 1^.+ to 3^.+.
Relative energies in kcal mol^-1

The cool part of this is why the barrier is so small leading out of 1^.+ – vibronic coupling via C_s distortion of 1^.+ with its first excited state leads to an energy lowering of this pathway. This sort of vibronic coupling had in fact been implicated by Heilbronner and Wiberg³ in arguing the photoelectron spectrum of 1.

References

(1) Müller, B.; Bally, T.; Pappas, R.; Williams, F., "Spectroscopic and Computational Studies on the Rearrangement of Ionized [1.1.1]Propellane and Some of its Valence Isomers: The Key Role of Vibronic Coupling," J. Am. Chem. Soc. 2010, 132, 14649-14660, DOI: 10.1021/ja106024y

(2) Hiberty, P. C., "Vibronic coupling: Cage-breaking cascade," Nat. Chem. 2011, 3, 96-97, DOI: 10.1038/nchem.971

(3) Honegger, E.; Huber, H.; Heilbronner, E.; Dailey, W. P.; Wiberg, K. B., "The PE spectrum of [1.1.1]propellane: evidence for a non-bonding MO?," J. Am. Chem. Soc., 1985, 107, 7172-7174, DOI: 10.1021/ja00310a068

InChI

1: InChI=1/C5H6/c1-4-2-5(1,4)3-4/h1-3H2
InChIKey=ZTXSPLGEGCABFL-UHFFFAOYAJ

2: InChI=1/C5H6/c1-4-3-5(4)2/h1-3H2
InChIKey=ZNKWTJLYBOAVHI-UHFFFAOYAT

3^.+: InChI=1/C5H6/c1-4-5(2)3/h1-3H2/q+1
InChIKey=BVWPXIKADZQKEJ-UHFFFAOYAU

Once again, into the breach…

Ess, Liu, and De Proft offer another analysis of the protobranching effect.¹ As a reminder, Schleyer, Mo and Houk and coworkers argue that the reason why branched alkanes are more stable than linear ones is a stabilizing 1,3-interaction that they call protobranching.² This proposal has been met with both supporters and vigorous attacks – see these posts.

What is new here is a partitioning of the total DFT energy into three terms. The critical term is one based on the Weizäcker kinetic energy, which is defined as the integral of the gradient of the density squared divided by the density. They call this a “steric energy term”. The second term is the standard electrostatic term, and the last term, which really just picks up the slack, is a “fermionic quantum term”.

Using this partition, they examine a series of bond separation reactions involving alkanes with differing degrees of “protobranches”. The upshot is that the steric energy, which is destabilizing, is less in branched alkanes that linear ones. However, the fermionic quantum term essentially cancels this out, as branched alkanes, being more compact, are more destabilized by this fermionic effect than are linear alkanes. So, the only remaining term, electrostatics is responsible for the branched alkanes being more stable than linear alkanes.

This does not ultimately resolve the issue of whether the protobranching effect, as defined by Schleyer, Mo and Houk, is real, but these authors purposely chose to avoid that question.

References

(1) Ess, D. H.; Liu, S.; De Proft, F., "Density Functional Steric Analysis of Linear and Branched Alkanes," J. Phys. Chem. A, 2010, ASAP, DOI: 10.1021/jp108577g

(2) Wodrich, M. D.; Wannere, C. S.; Mo, Y.; Jarowski, P. D.; Houk, K. N.; Schleyer, P. v. R., "The Concept of Protobranching and Its Many Paradigm Shifting Implications for Energy Evaluations," Chem. Eur. J. 2007, 13, 7731-7744, DOI: 10.1002/chem.200700602

Jacobsen reports another interesting example of organocatalysis, here using a chiral guanadinium salt to catalyze the enantioselective Claisen rearrangement.¹ As an example, Reaction 1 proceeds in 6 days at 30 °C to give 81% yield with an ee of 84%. The system is also diastereoselective, so that Reaction 2, run for 6 days at 40 °C, gives an 82% yield with a diastereomeric ratio of 16:1 and an ee of 81%.

B3LYP/6-31G(d,p) computations provide some insight. The uncatalyzed reaction of 1 to give 2 is predicted to be exothermic by 16.1 kcal mol^-1, with an activation energy of 25.9 kcal mol^-1. Using N,N’-dimethylguanidnium as a model for the catalyst (and with no counter anion and no treatment of solvent – hexanes in this case), they find a complexation energy of almost 27 kcal mol^-1 for forming 3. 3 exhibits (See Figure 1) three hydrogen bond-like interactions – one N-H bifurcates to interact with the carbonyl oxygen and (a very long interaction) to the other oxygen. The product complex 4 also shows three hydrogen bond-like interactions, with an overall exothermicity of -14.7 kcal mol^-1. The complexed transition state 5 has two normal length hydrogen bonds, with an activation energy above 3 of 20.6 kcal mol^-1. Thus the complex lowers the barrier by about 5 kcal mol^-1, indicating the catalytic effect. They have not however addressed the enantioselectivity.

3	5
4

Figure 1. B3LYP/6-31G(d,p) optimized geometries of 3-5.

References

(1) Uyeda, C.; Rötheli, A. R.; Jacobsen, E. N., "Catalytic Enantioselective Claisen Rearrangements of O-Allyl β-Ketoesters," Angew. Chem. Int. Ed., 2010, 49, 9753–9756, DOI: 10.1002/anie.201005183

InChIs

1: InChI=1/C10H14O3/c1-3-7-13-9-6-4-5-8(9)10(11)12-2/h3H,1,4-7H2,2H3
InChIKey=NASFSRKGDOBHIX-UHFFFAOYAC

2: InChI=1/C10H14O3/c1-3-6-10(9(12)13-2)7-4-5-8(10)11/h3H,1,4-7H2,2H3/t10-/m0/s1
InChIKey=QXKXLNGEBVMWLH-JTQLQIEIBT