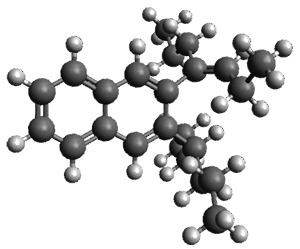
I have posted on the use of computed NMR chemical shifts and coupling constants to help aid in structure identification. The second edition of my book Computational Organic Chemistry has a largely all-new chapter on structure identification aided by computed spectra, especially NMR spectra. In my recent opinion piece speculating on challenges in computational organic chemistry,¹ the first area I highlight is encouraging the larger use of computed spectra as an essential component of structure determination.

While more and more non-traditional computational users are employing quantum computations towards these problems, I suspect that many non-users are a bit wary about stepping into an arena they are not expert in, an arena chock-filled with acronyms and methods and potentially little guidance. While some very nice papers^2-6 and web sites (Chemical Shift Repository (Cheshire) and DP4) do outline procedures for using computations in this fashion, they are not truly designed for the non-specialist.

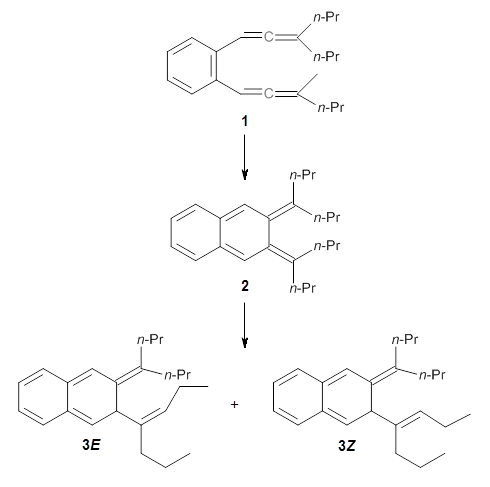
Well, fear not any longer. Hoye and coworkers, synthetic chemists who have utilized computational approaches in structure determinations for a number of years, have written a detailed step-by-step protocol for using a standard computational approach towards structure determination.⁷ The article is written with the synthetic chemist in mind, and includes a number of scripts to automate many of the steps.

For the specialist, the overall outline of the protocol is fairly routine:

1. Utilize MacroModel to perform a conformational search for each proposed structure, retaining the geometries within 5 kcal mol^-1 of the global minimum.
2. Optimize these conformations for each structure at M06-2x/6-31+G(d).
3. For each conformation of each structure, compute the ¹H and ¹³C chemical shifts, scale them, and determine the Boltzmann weighted chemical shifts
4. Compare these chemical shifts with the experimental values using Mean Absolute Error

The article is straightforward and easily guides the novice user through these steps. Anyone unsure of how to utilize quantum chemical computations in structure determination is well advised to start with this article.

References

(1) Bachrach, S. M. "Challenges in computational organic chemistry," WIRES: Comput. Mol. Sci. 2014, 4, 482-487, DOI: 10.1002/wcms.1185.

(2) Lodewyk, M. W.; Siebert, M. R.; Tantillo, D. J. "Computational Prediction of ¹H and ¹³C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry," Chem. Rev. 2012, 112, 1839–1862, DOI: 10.1021/cr200106v.

(3) Bally, T.; Rablen, P. R. "Quantum-Chemical Simulation of ¹H NMR Spectra. 2. Comparison of DFT-Based Procedures for Computing Proton-Proton Coupling Constants in Organic Molecules," J. Org. Chem. 2011, 76, 4818-4830, DOI: 10.1021/jo200513q.>

(4) Jain, R.; Bally, T.; Rablen, P. R. "Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets," J. Org. Chem. 2009, 74, 4017-4023, DOI: 10.1021/jo900482q.

(5) Smith, S. G.; Goodman, J. M. "Assigning the Stereochemistry of Pairs of Diastereoisomers Using GIAO NMR Shift Calculation," J. Org. Chem. 2009, 74, 4597-4607, DOI: 10.1021/jo900408d.

(6) Smith, S. G.; Goodman, J. M. "Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability," J. Am. Chem. Soc. 2010, 132, 12946-12959, DOI: 10.1021/ja105035r.

(7) Willoughby, P. H.; Jansma, M. J.; Hoye, T. R. "A guide to small-molecule structure assignment through computation of (1H and 13C) NMR chemical shifts," Nat. Protocols 2014, 9, 643-660, DOI: 10.1038/nprot.2014.042.

Here’s another cruel and unusual punishment applied to the poor benzene ring. Hashimoto,et al. have created a molecule that is a fused double helicene, where the fusion is about a single phenyl ring.¹ Compound 1 has two [5]helicenes oriented in opposite directions. This should provide a twist to the central phenyl ring, and the added methyl groups help to expand that twist.

They prepared 1 and its x-ray crystal structure is reported. The compound exhibits C₂ symmetry. The twist (defined as the dihedral of four consecutive carbon atoms of the central ring) is 28.17°, nearly the same twist as in [2]paraphenylene.

The B3LYP/6-31G(d) structure of 1 is shown in Figure 1. This geometry is very similar to the x-ray structure. The calculated NICS value for the central ring is -4.9 (B3LYP/6-311+G(d,p)/B3LYP/6-31G(d)) and -4.3 (B3LYP/6-311+G(d,p)/x-ray structure). This diminished value from either benzene or C₆(PSH₂)₂(CH₃)₄ indicates reduced aromaticity of this central ring, presumably due to the distortion away from planarity. Nonetheless, the central ring of 1 is not oxidized when subjected to MCPBA to oxidize to the bis phosphine oxides.

1

Figure 1. B3LYP/6-31G(d) optimized structure of 1.

References

(1) Hashimoto, S.; Nakatsuka, S.; Nakamura, M.; Hatakeyama, T. "Construction of a Highly Distorted Benzene Ring in a Double Helicene," Angew. Chem. Int. Ed. 2014, 53, 14074-14076, DOI: 10.1002/anie.201408390.

InChIs

1: InChI=1S/C50H32P2S2/c1-25-17-21-29-9-5-13-33-41(29)37(25)45-46-38-26(2)18-22-30-10-7-15-35(42(30)38)52(54)36-16-8-12-32-24-20-28(4)40(44(32)36)48(50(46)52)47-39-27(3)19-23-31-11-6-14-34(43(31)39)51(33,53)49(45)47/h5-24H,1-4H3

In solution ortho-phenylenes preferentially coil into a helix with the phenyl rings stacked. However, 25-50% of these chains will typically misfold. Hartley and coworkers have reported the use of substituents to increase the percentage of perfectly folded chains.¹

They synthesized two isomeric o-phenylenes, differing in the substitution pattern (1 and 2), with chain length of 6 to 10 phenyl rings. Substituents included methoxy, acetoxy, nitrile, and triflate. They principally employed ¹H NMR to assess the conformational distribution, and used computations to confirm the conformation.

Ideally folded conformations of 1 and 2 with eight phenyl rings are shown in Figure 1. The dihedral angle formed by two adjacent phenyl rings are typically about ±55° or ±130°.

1

2

Figure 1. Idealized folding of 1 and 2 with X=OH.
Hydrogens omitted in these images, but full structures available, through Jmol, by clicking on the image.)

Given the size of these systems, and the conformation flexibility not just of the chain but with each substituent, a full search to identify the global minimum was not undertaken. Rather, a library of conformations was generated with MM, the lowest 200 conformations were then reoptimized at PM7 and then the energies were determined at PCM/B97-D/TZV(2d,2p). The lowest energy conformer was then reoptimized at this DFT level. Three conformations of 3 and 4 are shown in Figure 2 with triflate as the substituent with six phenyl rings. The first conformer has optimal stacking (perfect folding), the second conformer as one misfold at the end, and the third conformer has no stacking at all.

3 – ideal fold	3 – one misfold
3 – all misfold
4 – ideal fold	4 – one misfold
4 – all misfold

Figure 2. Optimized geometries of conformers of 3 and 4.
(Remember that clicking on one of these images will bring up the JMol applet allowing you to rotate and visualize the molecule in 3-D – a very useful feature here!)

NMR chemical shifts were then computed using these geometries at PCM/WP04/6-31G(d). In all cases examined, the chemical shifts of the major conformation was confirmed to be the perfect folding one by comparison with the computed chemical shifts. The examined substituents enhanced the proportion of properly folded chains in all cases, often to the extent where no minor conformer was observed at all.

References

(1) Mathew, S.; Crandall, L. A.; Ziegler, C. J.; Hartley, C. S. "Enhanced Helical Folding of ortho-Phenylenes through the Control of Aromatic Stacking Interactions," J. Am. Chem. Soc. 2014, 136, 16666-16675, DOI:10.1021/ja509902m.

InChIs

3: InChI=1S/C42H26F18O18S6/c43-37(44,45)79(61,62,63)23-5-1-21(2-6-23)29-13-9-25(81(67,68,69)39(49,50)51)17-33(29)35-19-27(83(73,74,75)41(55,56)57)11-15-31(35)32-16-12-28(84(76,77,78)42(58,59)60)20-36(32)34-18-26(82(70,71,72)40(52,53)54)10-14-30(34)22-3-7-24(8-4-22)80(64,65,66)38(46,47)48/h1-20H,(H,61,62,63)(H,64,65,66)(H,67,68,69)(H,70,71,72)(H,73,74,75)(H,76,77,78)
InChIKey=BOCNJIZJHQKUNK-UHFFFAOYSA-N

4: InChI=1S/C42H26F18O18S6/c43-37(44,45)79(61,62,63)23-6-4-21(5-7-23)33-17-25(81(67,68,69)39(49,50)51)9-13-30(33)35-19-27(83(73,74,75)41(55,56)57)11-15-32(35)36-20-28(84(76,77,78)42(58,59)60)10-14-31(36)34-18-26(82(70,71,72)40(52,53)54)8-12-29(34)22-2-1-3-24(16-22)80(64,65,66)38(46,47)48/h1-20H,(H,61,62,63)(H,64,65,66)(H,67,68,69)(H,70,71,72)(H,73,74,75)(H,76,77,78)
InChIKey=YKSIXAVDGFBUIZ-UHFFFAOYSA-N

With the proliferation of density functionals, selecting the functional to use in your particular application requires some care. That is why there have been quite a number of benchmark studies (see these posts for some examples). Yu and Karton have now added to our benchmark catalog with a study of π-conjugation.¹

They looked at a set of 60 reactions which involve a reactant with π-conjugation and a product which lacks conjugation. A few examples, showing examples involving linear and cyclic systems, are shown in Scheme 1.

Scheme 1.

The reaction energies were evaluated at W2-F12, which should have an error of a fraction of a kcal mol^-1. Three of the reactions can be compared with experimental values, and difference in the experimental and computed values are well within the error bars of the experiment. It is too bad that the authors did not also examine 1,3-cyclohexadiene → 1,4-cyclohexadiene, a reaction that is both of broader interest than many of the ones included in the test set and can also be compared with experiment.

These 60 reactions were then evaluated with a slew of functionals from every rung of Jacob’s ladder. The highlights of this benchmark study are that most GGA and meta-GGA and hybrid functionals (like B3LYP) have errors that exceed chemical accuracy (about 1 kcal mol^-1). However, the range-separated functionals give very good energies, including ωB97X-D. The best results are provided with double hybrid functionals. Lastly, the D3 dispersion correction does generally improve energies by 10-20%. On the wavefunction side, SCS-MPs gives excellent results, and may be one of the best choices when considering computational resources.

References

(1) Yu, L.-J.; Karton, A. "Assessment of theoretical procedures for a diverse set of isomerization reactions involving double-bond migration in conjugated dienes," Chem. Phys. 2014, 441, 166-177, DOI: 10.1016/j.chemphys.2014.07.015.

Schmittel has examined the thermolysis of 1, which undergoes a Garratt-Braverman rearrangement followed by a [1,5]-H migration to produce 3.¹ The product 3 is formed in a 10.3:1 ratio of E to Z consistently over the temperature range of 60 – 140 °C. This non-changing ratio is unusual. The difference in the computed (UB3LYP/6-31g(d)) free energy of activation for the step 2 → 3 ranges from 2.35 to 2.56 kcal mol^-1 for this temperature range, manifesting in a predicted E:Z ratio of 24.9 at 60 °C to 22.7 at 140 °C.

The computed structures of 1-3 along with the transition states are shown in Figure 1. The activation free energy for the first step (Garrat-Braverman) is 30.9 kcal mol^-1. This is about 30 kcal mol^-1 larger than the barrier for the second step. Schmittel suggests that a non-statistical effect is manifesting here. The molecule crosses the first TS and then follows a downhill path directly over TS2E without spending any time in the region of the intermediate 2. A few computed trajectories all indicate that it takes less than 50 fs from the time the reaction crosses TS1 until the hydrogen migrates, supporting the notion that vibrational relaxation within the intermediate 2 is not occurring. This reaction is yet another example of dynamic effects dictating product distributions.

1a 0.0	1b 12.3
TS1 30.9	2 -14.6
TS2E 0.5	TS2Z 2.8
3E -50.5	3Z -46.1

Figure 1. UB3LYP/6-31G(d) optimized structures and relative free energies (kcal mol^-1) for the reaction 1 → 3. (Note that a conformational change must first take 1a into 1b before the reaction can take place.)

References

1) Samanta, D.; Rana, A.; Schmittel, M. “Nonstatistical Dynamics in the Thermal Garratt−Braverman/[1,5]‑H Shift of One Ene−diallene: An Experimental and Computational Study,” J. Org. Chem. 2014, 79, 8435–8439, DOI: 10.1021/jo501324w.

InChIs

1: InChI=1S/C24H34/c1-5-11-21(12-6-2)17-19-23-15-9-10-16-24(23)20-18-22(13-7-3)14-8-4/h9-10,15-16,19-20H,5-8,11-14H2,1-4H3
InChIKey=RVCDLAOAATXCKZ-UHFFFAOYSA-N

2: InChI=1S/C24H34/c1-5-11-19(12-6-2)23-17-21-15-9-10-16-22(21)18-24(23)20(13-7-3)14-8-4/h9-10,15-18H,5-8,11-14H2,1-4H3
InChIKey=QCHALYJSTFUUQF-UHFFFAOYSA-N

3E; InChI=1S/C24H34/c1-5-11-19(12-6-2)23-17-21-15-9-10-16-22(21)18-24(23)20(13-7-3)14-8-4/h9-11,15-18,23H,5-8,12-14H2,1-4H3/b19-11-
InChIKey=XWILUXHXXNRMRE-ODLFYWEKSA-N

3Z: InChI=1S/C24H34/c1-5-11-19(12-6-2)23-17-21-15-9-10-16-22(21)18-24(23)20(13-7-3)14-8-4/h9-11,15-18,23H,5-8,12-14H2,1-4H3/b19-11+
InChIKey=XWILUXHXXNRMRE-YBFXNURJSA-N

In trying to clean up my in-box of articles for potential posts, I write here about two articles for a more general audience, authored by two of the major leaders in computational organic chemistry.

Ken Houk offers an overview of how computational simulation is a partner with experiment and theory in aiding and guiding our understanding of organic chemistry.¹ The article is written for the non-specialist, really even more for the non-scientist. Ken describes how computations have helped understand relatively simple reactions like pericyclic reactions, that then get more subtle when torquoselection is considered, to metal-catalysis, to designed protein catalysts. If you are ever faced with discussing just what you do as a computational chemist at a cocktail party, this article is a great resource of how to explain our science to the interested lay audience.

Paul Schleyer adds a tutorial on transition state aromaticity.² The authors discusses a variety of aromaticity measures (energetics, geometry, magnetic properties) that can be employed to analyze the nature of transition states, in addition to ground state molecules. This article provides a very clear description of the methods and a few examples. It is written for a more specialized audience than Houk’s article, but is nonetheless completely accessible to any chemist, even those with no computational background.

References

(1) Houk, K. N.; Liu, P. "Using Computational Chemistry to Understand & Discover Chemical Reactions," Daedalus 2014, 143, 49-66, DOI: 10.1162/DAED_a_00305.

(2) Schleyer, P. v. R.; Wu, J. I.; Cossio, F. P.; Fernandez, I. "Aromaticity in transition structures," Chem. Soc. Rev. 2014, 43, 4909-4921, DOI: 10.1039/C4CS00012A.

Three-dimensional objects can be projected into four-dimensional objects. So for example a cube can be projected into a hypercube, as in Scheme 1.

Scheme 1.

Pichierri proposes a hydrocarbon analogue of the hypercube. The critical decision is the connecting bridge between the outer (exploded) carbons. This distance is too long to be a single carbon-carbon bond. Pichierri opts to use ethynyl bridges, to give the hypercube 1.¹

Now, unfortunately he does not supply any supporting materials. So I have reoptimized this O_h geometry at B3LYP/6-31G(d), and show this structure in Figure 1. Pichierri does not report much beyond the geometry of 1 and the perfluoronated analogue. One interesting property that might be of interest is the ring strain energy of 1, which I will not take up here.

But a question I will take up is just what bridges might serve to create the hydrocarbon hypercube. A more fundamental choice might be ethanyl bridges, to create 2. However, the O_h conformer of 2 has 13 imaginary frequencies at B3LYP/6-31G(d). Lowering the symmetry to D₃ give a structure that has only real frequencies, and it’s shown in Figure 1. An interesting exercise is to ponder other choices of bridges, which I will leave for the reader.

1

2

Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2.
As always, be sure to click on the image to enable Jmol for interactive viewing of these interesting structures!

References

(1) Pichierri, F. "Hypercubane: DFT-based prediction of an O_h-symmetric double-shell hydrocarbon," Chem. Phys. Lett. 2014, 612, 198-202, DOI: j.cplett.2014.08.032.

InChIs

1: InChI=1S/C40H24/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H
InChIKey=FFMFUIDOGFAUOP-UHFFFAOYSA-N

2: InChI=1S/C40H48/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H2
InChIKey=MCSZKKKJCDSRIV-UHFFFAOYSA-N

I remain amazed at how regularly I read reports of structure determinations of what seem to be simple molecules, yet these structures have eluded determination for decades if not centuries. An example is the recently determined x-ray crystal structure of L-phenylalanine;¹ who knew that growing these crystals would be so difficult?

The paper I want to discuss here is on the gas-phase structure of carbonic acid 1.² Who would have thought that preparing a pure gas-phase sample would be so difficult? Schreiner and co-workers prepared carbonic acid by high-vacuum flash pyrolysis (HVFP) of di-tert-butyl carbonate, as shown in Scheme 1.

Scheme 1

Carbonic acid can appear in three difference conformations, shown in Figure 1. The two lowest energy conformations are separated by a barrier of 9.5 kcal mol^-1 (estimated by focal point energy analysis). These conformations can be interconverted using near IR light. The third conformation is energetically inaccessible.

1cc (0.0)	1ct (1.6)	1tt (10.1)
2cc		2cc

Figure 1. CCSD(T)/cc-pVQZ optimized structures of 1 (and the focal point relative energies in kcal mol^-1) and the CCSD(T)/cc-pVTZ optimized structures of 2.

The structures of these two lowest energy conformations were confirmed by comparing their experimental IR spectra with the computed spectra (CCSD(T)/cc-pVTZ) and their experimental and computed rotational constants.

An interesting added component of this paper is that sublimation of the α- and β-polymorphs of carbonic acid do not produce the same compound. Sublimation of the β-isomorph does produce 1, but sublimation of the α-isomorph produces the methylester of 1, compound 2 (see Figure 1). The structure of 2 is again confirmed by comparison of the experimental and computed IR spectra.

References

(1) Ihlefeldt, F. S.; Pettersen, F. B.; von Bonin, A.; Zawadzka, M.; Görbitz, C. H. "The Polymorphs of L-Phenylalanine," Angew. Chem. Int. Ed. 2014, 53, 13600–13604, DOI: 10.1002/anie.201406886.

(2) Reisenauer, H. P.; Wagner, J. P.; Schreiner, P. R. "Gas-Phase Preparation of Carbonic Acid and Its Monomethyl Ester," Angew. Chem. Int. Ed. 2014, 53, 11766-11771, DOI: 10.1002/anie.201406969.>

InChIs

1: InChI=1S/CH2O3/c2-1(3)4/h(H2,2,3,4)
InChIKey=BVKZGUZCCUSVTD-UHFFFAOYSA-N

2: InChI=1S/C2H4O3/c1-5-2(3)4/h1H3,(H,3,4)
InChIKey=CXHHBNMLPJOKQD-UHFFFAOYSA-N

Professor Paul von Ragué Schleyer passed away November 21, 2014. Paul was a major force in physical organic and computational organic chemistry. I followed his career closely for the entirety of my own career; my doctoral studies with Andrew Streitwieser involved the analysis of the nature of the C-Li bond and we were in constant communication with Schleyer. Paul’s work on aromaticity greatly informed my thinking and my studies in this area.

I interviewed Paul in his office at the University of Georgia for the first edition of my book Computational Organic Chemistry. This interview was reprinted in the second edition without any changes. In honor of Paul, I am posting this interview here, so that our community can remember this important, inspirational figure.

The Alonso group has yet again (see these posts) determined the gas-phase structure of an important, biologically significant molecule using a combination of exquisite microwave spectroscopy and quantum computations. This time they examine the structure of histidine.¹

They optimized four conformations of histidine, as its neutral tautomer, at MP2/6-311++G(d,p). These are schematically drawn in Figure 1. Conformer 1a is the lowest in free energy, likely due to the two internal hydrogen bonds. Its structure is shown in Figure 2.

Figure 1. The four conformers of histidine. The relative free energy (MP2/6-311++G(d,p)) in kcal mol^-1 are also indicated.

Figure 2. MP2/6-311++G(d,p) optimized geometry of 1a.

The initial experimental rotation constants were only able to eliminate 1b from consideration. So they then determined the quadrupole coupling constants for the ¹⁴N nuclei. These values strongly implicated 1a as the only structure in the gas phase. The agreement between the experimental values and the computed values at MP2/6-311++G(d,p) was a concern, so they rotated the amine group to try to match the experimental values. This lead to a change in the NHCC dihedral value of -16° to -23° Reoptimization of the structure at MP2/cc-pVTZ led to a dihedral of -21° and overall excellent agreement between the experimental spectral parameters and the computed values.

It is somewhat disappointing the supporting materials does not include the structures of the other three isomers, nor the optimized geometry at MP2/cc-pVTZ.

References

1) Bermúdez, C.; Mata, S.; Cabezas, C.; Alonso, J. L. "Tautomerism in Neutral Histidine," Angew. Chem. Int. Ed. 2014, 53, 11015-11018, DOI: 10.1002/anie.201405347.

InChIs

Histidine: InChI=1S/C6H9N3O2/c7-5(6(10)11)1-4-2-8-3-9-4/h2-3,5H,1,7H2,(H,8,9)(H,10,11)/t5-/m0/s1
InChIKey=HNDVDQJCIGZPNO-YFKPBYRVSA-N