Three-dimensional objects can be projected into four-dimensional objects. So for example a cube can be projected into a hypercube, as in Scheme 1.
Scheme 1.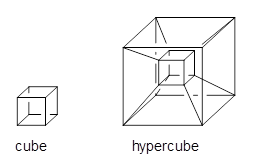
Pichierri proposes a hydrocarbon analogue of the hypercube. The critical decision is the connecting bridge between the outer (exploded) carbons. This distance is too long to be a single carbon-carbon bond. Pichierri opts to use ethynyl bridges, to give the hypercube 1.1
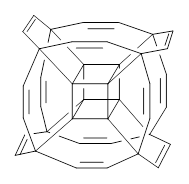
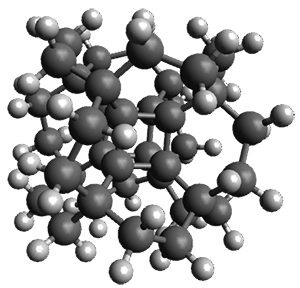
Now, unfortunately he does not supply any supporting materials. So I have reoptimized this Oh geometry at B3LYP/6-31G(d), and show this structure in Figure 1. Pichierri does not report much beyond the geometry of 1 and the perfluoronated analogue. One interesting property that might be of interest is the ring strain energy of 1, which I will not take up here.
|
|
2 |
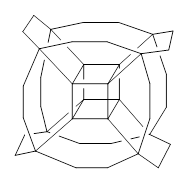
But a question I will take up is just what bridges might serve to create the hydrocarbon hypercube. A more fundamental choice might be ethanyl bridges, to create 2. However, the Oh conformer of 2 has 13 imaginary frequencies at B3LYP/6-31G(d). Lowering the symmetry to D3 give a structure that has only real frequencies, and it’s shown in Figure 1. An interesting exercise is to ponder other choices of bridges, which I will leave for the reader.
|
1 |
2 |
Figure 1. B3LYP/6-31G(d) optimized structures of 1 and 2.
As always, be sure to click on the image to enable Jmol for interactive viewing of these interesting structures!
References
(1) Pichierri, F. "Hypercubane: DFT-based prediction of an Oh-symmetric double-shell hydrocarbon," Chem. Phys. Lett. 2014, 612, 198-202, DOI: j.cplett.2014.08.032.
InChIs
1: InChI=1S/C40H24/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H
InChIKey=FFMFUIDOGFAUOP-UHFFFAOYSA-N
2: InChI=1S/C40H48/c1-2-26-7-9-29-15-11-27-5-3-25(1)4-6-28-12-16-30(10-8-26)20-23-32(22-19-29)24-21-31(17-13-27,18-14-28)39-35(27)33(25)34(26)37(29,35)40(32,39)38(30,34)36(28,33)39/h1-24H2
InChIKey=MCSZKKKJCDSRIV-UHFFFAOYSA-N

Fabio Pichierri responded on 09 Jan 2015 at 1:00 am #
Thanks for your comments Steve! My paper also contains the geometry of the hollow hypercubane molecule (and its fluorinated analogue) where the inner C8 cube is replaced with Hs along with an analysis of the frontier MOs and theoretical 13-C and 1-H NMR chemical shifts (for spectroscopic identification). As for the bridges, I thought about possible alternatives but did not come up with an interesting idea (of course one could try to use heteroatoms such as sulfur or selenium or a metal for the bridges).
The beauty of the hypercubane geometry is overwhelming. Let me explain you how I came up with this structure. In 2011 I saw the movie “Captain America: The First Avenger” and I was intrigued by the tesseract, a magical object hold by the main villain character (Red Skull). After some research about it I thought about possible ways to build a molecular analogue starting from cubane. Once I optimized the 3D model, I was flabbergasted by its beauty and high symmetry. For the next three years I almost forgot about it and in 2014 I decided to write up the paper. I hope that some brave synthetic organic chemist may be able to synthesize it in the future. If not, it will remain a curiosity among many other computed molecules published in the literature. Cheers, Fabio
Fabio Pichierri responded on 21 Jan 2016 at 9:26 pm #
The story on hypercubane continues: recently Maslov and Katin [1] investigated the kinetic stability of hypercubane by tight-binding molecular dynamics simulation. The simulations, performed in the range 1000-2000 K, indicate that this compound would be characterized by high kinetic stability and a RT life time of 10^14 s. Furthermore, the decomposition of hypercubane would result in the loss of three acetylene molecules yielding an airscrew-like decomposition product.
[1] M.M. Maslov & K.P. Katin, “High kinetic stability of hypercubane: Tight-binding molecular dynamics study”, Chem. Phys. Lett. 644 (2016) 280-283, DOI: j.cplett.2015.12.022