An emerging theme in this blog is Möbius systems, ones that can be aromatic or antiaromatic. Rzepa has led the way here, especially in examining annulenes with a twisted structure. Along with Schleyer and Schaefer, they have now explored a series of Möbius annulenes.¹ The particularly novel aspect of this new work is the examination of higher-order Möbius systems. In the commonly held notion of the Möbius strip, the strip contains a single half twist. Rzepa points out that the notion of twist must be considered as two parts, a part due to torsions and a part due to writhe.² We can think of the Möbius strip as formed by a ladder where the ends are connect such that the left bottom post connects with the top right post and the bottom right post connects with the top left post. Let’s now consider the circle created by joining the midpoints of each rug of the ladder. If this circle lies in a plane, then the torsion is π/N where N is the number of rungs in the ladder. But, the collection of midpoints does not have to lie in a plane, and if these points distort out of plane, that’s writhe and allows for less torsion in the strip.The sum of these two parts is called L_k and it will be an integral multiple of π. So the common Möbius strip has L_k = 1.

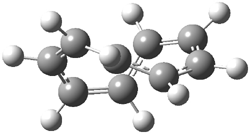
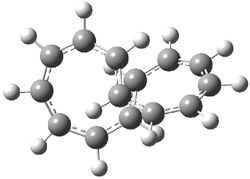
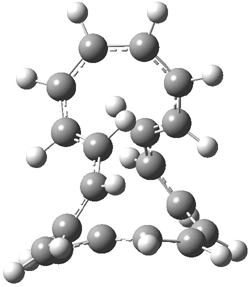
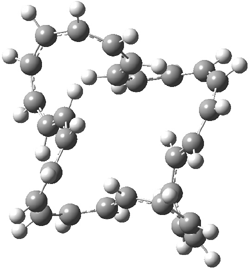
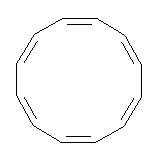
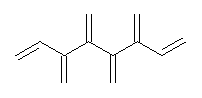
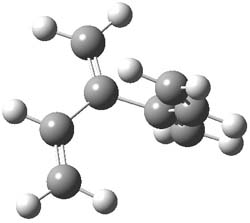
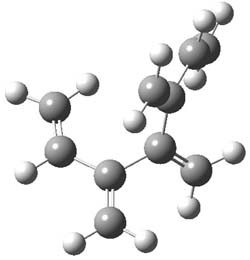
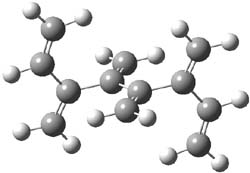
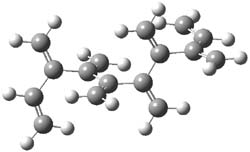
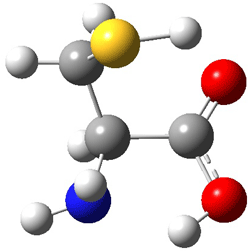
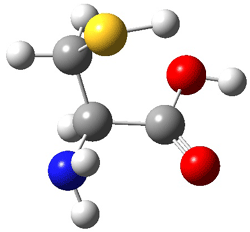
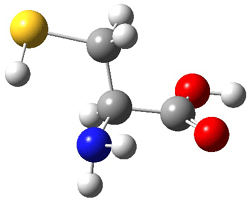
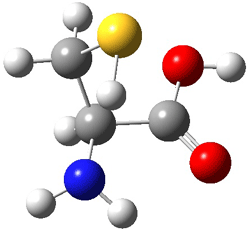
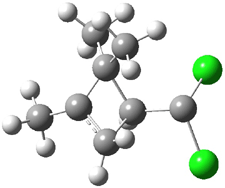
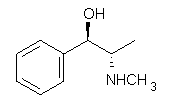
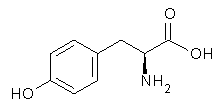
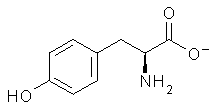
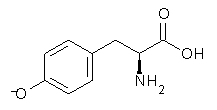
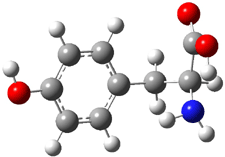
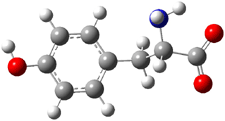
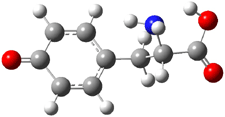
An example of a molecular analogue of the common Möbius strip is the annulene C₉H₉⁺ (1) – see figure 1. But Möbius strips can have more than one twist. Rzepa, Schleyer, and Schaefer have found examples with L_k = 2, 3, or 4. Examples are C₁₄H₁₄ (2) with one full twist (L_k = 2, two half twists), C₁₆H₁₆^2- (3) with three half twists, and C₂₀H₂₀²⁺ (4) with four half twists.

1	2
3	4

Figure 1. Structures of annulenes 1-4.

These annulenes with higher-order twisting, namely 2-4, are aromatic, as determined by a variety of measures. For example, all express negative NICS values, all have positive diagmagnetic exaltations, and all express positive isomerization stabilization energies (which are a measure of aromatic stabilization energy).

References

(1) Wannere, C. S.; Rzepa, H. S.; Rinderspacher, B. C.; Paul, A.; Allan, C. S. M.; Schaefer Iii, H. F.; Schleyer, P. v. R., "The Geometry and Electronic Topology of Higher-Order Charged M&oml;bius Annulenes" J. Phys. Chem. A 2009, ASAP, DOI: 10.1021/jp902176a

(2) Fowler, P. W.; Rzepa, H. S., "Aromaticity rules for cycles with arbitrary numbers of half-twists," Phys. Chem. Chem. Phys. 2006, 8, 1775-1777, DOI: 10.1039/b601655c.

Here’s another fine paper from the Alonso group employing laser ablation molecular beam Fourier transform microwave spectroscopy coupled with computation to discern molecular structure. In this work they examine the low-energy tautomers of guanine.1 The four lowest energy guanine tautomers are shown in Figure 1. (Unfortunately, Alonso does not include the optimized coordinates of these structures in the supporting information – we need to more vigorously police this during the review process!) These tautomers are predicted to be very close in energy (MP2/6-311++G(d,p), and so one might expect to see multiple signals in the microwave originating from all four tautomers. In fact, they discern all four, and the agreement between the computed and experimental rotational constants are excellent (Table 1), especially if one applies a scaling factor of 1.004. Once again, this group shows the power of combined experiment and computations!

Figure 1. Four lowest energy (kcal mol^-1, MP2/6-311++G(d,p)) tautomers of guanine.

Table 1. Experimental and computed rotational constants (MHz) of the four guanine tautomers.

References

(1) Alonso, J. L.; Peña, I.; López, J. C.; Vaquero, V., "Rotational Spectral Signatures of Four Tautomers of Guanine," Angew. Chem. Int. Ed. 2009, 48, 6141-6143, DOI: 10.1002/anie.200901462

InChIs

Guanine: InChI=1/C5H5N5O/c6-5-9-3-2(4(11)10-5)7-1-8-3/h1H,(H4,6,7,8,9,10,11)/f/h8,10H,6H2
InChIKey=UYTPUPDQBNUYGX-GSQBSFCVCX

Conjugated alkenes have played a major role in conceptualizing organic chemistry. Linear and cyclic unbranched conjugated alkenes have been well studied; the latter class comprising the aromatic and antiaromatic annulenes. The cyclic branched conjugate alkenes are known as radialenes and have been subject of some study. But the last category, the linear branched conjugated alkenes have been overlooked. Paddon-Row and Sherburn¹ now report a general synthetic method for preparing these species, which they call dendralenes, see Scheme 1.

Scheme 1. Classes of conjugated alkenes

The dendralenes fall into two groups – those with an odd number of double bonds and those with an even number. While the UV/Vis absorption maximum redshifts with increasing length, the molar extinctions coefficients are relatively constant for the odd denralenes but it increases by about 10,000 within the even dendralene family. The Diels-Alder chemistry is even more distinctive: the odd dendralenes react rapidly with an electron deficient dienophile (N-methylmaleimide), with rates decreasing slightly with increasing size, but the even dendralenes are significantly more sluggish.

The optimized B3LYP/6-31G(d) geometries of the lowest energy conformers of the [3]- to [8]dendralenes are shown in Figure 1. There are three types of butadiene fragments present in these structures: (a) near planar s-trans arrangement, (b) near perpendicular arrangement of the two double bonds, and (c) ­s-cis arrangement with the dihedral angle about 40°. The even dendralenes have only the first two type: alternating planar butadiene fragment that are more-or-less orthogonal to each other. The odd dendralenes all have at least one s-cis arrangement. Paddon-Row and Sherburn suggest that since the s-cis arrangement is necessary for the diene component of the Diels-SAlder reaction, the odd dendralenes are more reactive than the even ones since they have this arranegement in their ground state conformations, while the even dendralenes will have to react out of a higher energy conformation. This is a nice explanation readily formulated from simple computations.

[3]dendralene	[4]dendralene
[5]dendralene	[6]dendralene
[7]dendralene	[8]dendralene

Figure 1. B3LYP/6-31G(d) optimized structures of [3]- to [8]dendralene.¹

References

(1) Payne, A. D.; Bojase, G.; Paddon-Row, M. N.; Sherburn, M. S., "Practical Synthesis of the Dendralene Family Reveals Alternation in Behavior," Angew. Chem. Int. Ed. 2009, 48, 4836-4839, DOI: 10.1002/anie.200901733

InChIs

[3]dendralene: InChI=1/C6H8/c1-4-6(3)5-2/h4-5H,1-3H2
InChIKey=VXBVLYQDVVHAHZ-UHFFFAOYAS

[4]dendralene: InChI=1/C8H10/c1-5-7(3)8(4)6-2/h5-6H,1-4H2
InChIKey=DMCINEDFOKMBFI-UHFFFAOYAV

[5]dendralene: InChI=1/C10H12/c1-6-8(3)10(5)9(4)7-2/h6-7H,1-5H2
InChIKey=XEZCEXNNZGLEHB-UHFFFAOYAM

[6]dendralene: InChI=1/C12H14/c1-7-9(3)11(5)12(6)10(4)8-2/h7-8H,1-6H2
InChIKey=RBABOPLFRQKABD-UHFFFAOYAA

[7]dendralene: InChI=1/C14H16/c1-8-10(3)12(5)14(7)13(6)11(4)9-2/h8-9H,1-7H2
InChIKey=ZIBYAXDRKFGSBF-UHFFFAOYAH

[8]dendralene: InChI=1/C16H18/c1-9-11(3)13(5)15(7)16(8)14(6)12(4)10-2/h9-10H,1-8H2
InChIKey=YWPORNAHEZCVCQ-UHFFFAOYAR

Schaefer, Csaszar, and Allen have applied the focal point method towards predicting the energies and structures of cysteine.¹ This very high level method refines the structures that can be used to compare against those observed by Alonso² in his laser ablation molecular beam Fourier transform microwave spectroscopy experiment (see this post). They performed a broad conformation search, initially examining some 66,664 structures. These reduced to 71 unique conformations at MP2/cc-pvTZ. The lowest 11 energy structures were further optimized at MP2(FC)/aug-cc-pV(T+d)Z. The four lowest energy conformations are shown in Figure 1 along with their relative energies.

I (0.0)	II (4.79)
III (5.81)	IV (5.95)

Figure 1. MP2(FC)/aug-cc-pV(T+d)Z optimized geometries and focal point relative energies (kJ mol^-1) of the four lowest energy conformers of cysteine.¹

The three lowest energy structures found here match up with the lowest two structures found by Alonso and the energy differences are also quite comparable: 4.79 kJ and 5.81 mol^-1 with the focal point method 3.89 and 5.38 kJ mol^-1 with MP4/6-311++G(d,p)// MP2/6-311++G(d,p). So the identification of the cysteine conformers made by Alonso remains on firm ground.

References

(1) Wilke, J. J.; Lind, M. C.; Schaefer, H. F.; Csaszar, A. G.; Allen, W. D., "Conformers of Gaseous Cysteine," J. Chem. Theory Comput. 2009, DOI: 10.1021/ct900005c.

(2) Sanz, M. E.; Blanco, S.; López, J. C.; Alonso, J. L., "Rotational Probes of Six Conformers of Neutral Cysteine," Angew. Chem. Int. Ed. 2008, 4, 6216-6220, DOI: 10.1002/anie.200801337

InChIs

Cysteine:
InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)/t2-/m0/s1
InChIKey: XUJNEKJLAYXESH-REOHCLBHBU

A computational study of addition of singlet carbenes to bicyclobutanes reveals another potential energy surface where dynamics may be active. Rablen, Jones and co-workers examined the reaction of dichlorocarbene with bicyclobutane 1 and 1,2,2-trimethylbicyclobutane 2 (Reactions 1 and 2) using a number of computational techniques.¹

For reaction 1, they identified three reaction pathways. The first two involve the carbene approaching along the central C-C bond. Path A (Scheme 1) involves a single transition state that leads to product 3, with a barrier of 8.4 kcal mol^-1. The second pat (pathway B), leads to critical point 4, which is a transition state at HF/6-31G* and QCISD/6-31G* but is a local minimum at CCSD/6-31G*. This minimum however is very shallow, and vibrational energy will exceed the barriers about it. Both pathways indicate an asynchronous but concerted reaction. The last pathway (C) is for insertion of the carbine into the bridgehead C-C bond, leading to the bicyclo product 5. This barrier is very high, 27 kcal mol^-1, and so this path is unlikely to be competitive.

Experimental study of Reaction 2 showed that only 6 is produced.² Rablen and Jones identified six pathways where the carbene attacks 2 along the bridgehead bond (analogous to Paths A and B, except there are three rotamers and the attack can be at either bridgehead carbon) and the insertion path that leads to 8. Once again, this last pathway has a very large barrier and is non-competitive. Attack at the unsubstituted bridgehead carbons is favored over attack at the methyl-substituted bridgehead by 2-3 kcal mol^-1. The path that leads directly to 7 has a slightly lower barrier (0.4 kcal mol^-1) than the path that leads directly to 8. The analog of Path B leads here to a true intermediate 9 through a barrier 0.4 kcal mol^-1 higher than the barrier that leads to 7. This intermediate is shown in Figure 1.

Figure 1. CCSD/6-31G* structure of intermediate 9.¹

The energies of the barriers suggest that 7 will be the major product, but not the exclusive product. Rablen and Jones point out that intermediate 9 lies in a very shallow plateau and exit from this intermediate can lead to either 7 or 8. This sort of potential energy surface has been implicated in reactions that exhibit non-statistical behavior indicative of dynamic effects (see Chapter 7 of my book). Rablen and Jones speculate that dynamics might be dictating the product distribution in Reaction 2 as well. Confirmation awaits a molecular dynamics study.

References

(1) Rablen, P. R.; Paiz, A. A.; Thuronyi, B. W.; Jones, M., "Computational Investigation of the Mechanism of Addition of Singlet Carbenes to Bicyclobutanes," J. Org. Chem. 2009, DOI: 10.1021/jo900485z

(2) Jackson, J. E.; Mock, G. B.; Tetef, M. L.; Zheng, G.-x.; Jones, M., "Reactions of carbenes with bicyclobutanes and quadricyclane : Cycloadditions with two σ bonds," Tetrahedron 1985, 41, 1453-1464, DOI: 10.1016/S0040-4020(01)96386-0.

InChIs

1: InChI=1/C4H6/c1-3-2-4(1)3/h3-4H,1-2H2
InChIKey=LASLVGACQUUOEB-UHFFFAOYAV

2: InChI=1/C7H12/c1-6(2)5-4-7(5,6)3/h5H,4H2,1-3H3
InChIKey=GJMVYBBYZUWWLJ-UHFFFAOYAI

3: InChI=1/C5H6Cl2/c1-2-3-4-5(6)7/h2,4H,1,3H2
InChIKey=FGUOQAVVVDPABB-UHFFFAOYAR

5: InChI=1/C5H6Cl2/c6-5(7)3-1-4(5)2-3/h3-4H,1-2H2
InChIKey=SUZACPSWEYRCBD-UHFFFAOYAW

6: InChI=1/C8H12Cl2/c1-6(2)8(3,4)5-7(9)10/h5H,1H2,2-4H3
InChIKey=QIFFCMZJZYIIBA-UHFFFAOYAZ

7: InChI=1/C8H12Cl2/c1-6(2)7(3)4-5-8(9)10/h5H,4H2,1-3H3
InChIKey=MOELQSRRCNAPQV-UHFFFAOYAX

8: InChI=1/C8H12Cl2/c1-6(2)5-4-7(6,3)8(5,9)10/h5H,4H2,1-3H3
InChIKey=PRCOWYZGJRWGOB-UHFFFAOYAP

The Alonso group has once again shown the power of the combination of molecular beam Fourier transform microwave spectroscopy (MB-FTMW) coupled with computations. They examined ephedrine, norephedrine and pseudoephedrine and determined the low energy conformations of each.¹ I discuss just the ephedrine case here, but similar results were obtained for the other two compounds.

1

Ephedrine (1) has six potential conformations, differing by the rotation about the C-C bond and the orientation of the methyl group on the nitrogen. They optimized the 6 conformers at MP2/6-311+G(d,p) and corrected the energies for zero-point vibrational energies computed at B3LYP/6-311++G(d,p). The rotational constants and diagonal elements of the ¹⁴N quadrupole coupling tensor were computed and obtained by experiment. The comparison of these values (shown in Table 1) made possible the identification of three low energy conformers, labeled as AGa, AGb, and GGa. The structures are shown in Figure 1.

Table 1. Experimental and computed^a spectroscopic constants for three conformers of ephedrine.¹

AGa (0.0)	AGb (1.35)
GGa (0.73)

Figure 1. MP2/6-311+G(d,p) computed structures and relative energies (kcal mol^-1) of the three conformers of ephedrine.¹

The agreement between the experimental and computed spectroscopic values is very good, less than 1.5% for the rotational constants. This excellent agreement makes possible the identification of these three conformers. The experimental population ratio of N(AGa):N(GGa):N(AGb) is 20:4:1, in nice agreement with the computed values. Of structural interest here is the intramolecular O-H^…N hydrogen bond in each conformer. The authors also suggest a weak hydrogen bond-like interaction between the N-H and the benzene π-system.

References

(1) Alonso, J. L.; Sanz, M. E.; Lopez, J. C.; Cortijo, V., "Conformational Behavior of Norephedrine, Ephedrine, and Pseudoephedrine," J. Am. Chem. Soc., 2009, 131, 4320-4326, DOI: 10.1021/ja807674q.

InChIs

1: InChI=1/C10H15NO/c1-8(11-2)10(12)9-6-4-3-5-7-9/h3-8,10-12H,1-2H3/t8-,10-/m0/s1
InChIKey=KWGRBVOPPLSCSI-WPRPVWTQBH

I blogged on Bickelhaput’s examination of the stability of kinked vs. linear polycyclic aromatics¹ in this post. Bickelhaupt argued against any H^…H stabilization across the bay region, a stabilization that Matta and Bader² argued is present based on the fact that there is a bond path linking the two hydrogens.

Grimme and Erker have now added to this story.³ They prepared the dideuterated phenanthrene 1 and obtained its IR and Raman spectra. The splitting of the symmetric (a₁) and asymmetric (b₁) vibrational frequencies is very small 9-12 cm^-1. The computed splitting are in the same range, with very small variation with the computational methodology employed. The small splitting argues against any significant interaction between the two hydrogen (deuterium) atoms. Further, the sign of the coupling between the two vibrations indicates a repulsive interaction between the two atoms. These authors argue that the vibrational splitting is almost entirely due to conventional weak van der Waals interactions, and that there is no “bond” between the two atoms, despite the fact that a bond path connects them. This bond path results simply from two (electron density) basins forced to butt against each other by the geometry of the molecule as a whole.

References

(1) Poater, J.; Visser, R.; Sola, M.; Bickelhaupt, F. M., "Polycyclic Benzenoids: Why Kinked is More Stable than Straight," J. Org. Chem. 2007, 72, 1134-1142, DOI: 10.1021/jo061637p

(2) Matta, C. F.; Hernández-Trujillo, J.; Tang, T.-H.; Bader, R. F. W., "Hydrogen-Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals," Chem. Eur. J. 2003, 9, 1940-1951, DOI: 10.1002/chem.200204626

(3) Grimme, S.; Mück-Lichtenfeld, C.; Erker, G.; Kehr, G.; Wang, H.; Beckers, H. W., H., "When Do Interacting Atoms Form a Chemical Bond? Spectroscopic Measurements and Theoretical Analyses of Dideuteriophenanthrene," Angew. Chem. Int. Ed. 2009, 48, 2592-2595, DOI: 10.1002/anie.200805751

InChIs

1: InChI=1/C14H10/c1-3-7-13-11(5-1)9-10-12-6-2-4-8-14(12)13/h1-10H/i7D,8D
InChIKey=YNPNZTXNASCQKK-QTQOOCSTEC

Molecular structures can differ depending on phase, particularly between the gas and solution phase. Kass has looked at the protonation of 4-aminobenzoic acid. In water, the amino is its most basic site, but what is it in the gas phase? The computed relative energies of the protonation sites are listed in Table 1. If one corrects the B3LYP values for their errors in predicting the proton affinity of aniline and benzoic acid, the carbonyl oxygen is predicted to be the most basic site by 5.0 kcal mol^-1, in nice accord with the G3 prediction of 4.1 kcal mol^-1. Clearly, the structure depends on the medium.

Table 1. Computed relative proton affinities (kcal mol^-1) of 4-aminobenzoic acid.

Electrospray of 4-aminobenzoic acid from 3:1 methanol/water and 1:1 acetonitrile/water solutions gave different CID spectra. H/D exchange confirmed that electrospray from the emthanol/water solution gave the oxygen protonated species while that from the acetonitrile/water solution gave the ammonium species.

References

(1) Tian, Z.; Kass, S. R., “Gas-Phase versus Liquid-Phase Structures by Electrospray Ionization Mass Spectrometry,” Angew. Chem. Int. Ed., 2009, 48, 1321-1323, DOI: 10.1002/anie.200805392.

InChIs

4-aminobenzoic acid: InChI=1/C7H7NO2/c8-6-3-1-5(2-4-6)7(9)10/h1-4H,8H2,(H,9,10)/f/h9H
InChIKey=ALYNCZNDIQEVRV-BGGKNDAXCD

One more nail in the coffin of the widely disputed Le Clair structure of hexacyclinol is provided by the B97-2/cc-pVTZ/B3LYP/6-31G(d,p) computed proton and ¹³C NMR for the two “structures” (see my previous blog post for structures and background). These computations¹ are at a more rigorous level than those performed by Rychnovsky, and the addition of the proton spectrum helps clearly settle this issue. Rychnovsky’s structure is the correct one – the mean absolute error between the experimental and computed structure is half that for Rychnovsky structure. The computed coupling constants also are in much better agreement with the Rychnovsky structure. So, Bagno’s contribution accomplishes, I hope, two things: (1) convinces everyone that DFT NMR spectra can be an important tool in identifying natural product structure and (2) closes the book on hexacylinol!

References

(1) Saielli, G.; Bagno, A., "Can Two Molecules Have the Same NMR Spectrum? Hexacyclinol Revisited," Org. Lett. 2009, 11, 1409-1412, DOI: 10.1021/ol900164a.

Following on their prediction that the thiol of cysteine¹ is more acidic than the carboxylic acid group (see this post), Kass has examined the acidity of tyrosine 1.² Which is more acidic: the hydroxyl (leading to the phenoxide 2) or the carboxyl (leading to the carboxylate 3) proton?

Kass optimized the structures of tyrosine and its two possible conjugate bases at B3LYP/aug-cc-pVDZ, shown in Figure 1, and also computed their energies at G3B3. 2 is predicted to be 0.2 kcal mol^-1 lower in energy than 3 at B3LYP and slightly more stable at G3B3 (0.5 kcal mol^-1). However, both computational methods underestimate the acidity of acetic acid more than that of phenol. When the deprotonation energies are corrected for this error, the phenolic proton is predicted to be 0.4 kcal mol^-1 more acidic than the carboxylate proton at B3LYP and 0.9 kcal mol^-1 more acidic at G3B3.

1
2	3

Figure 1. B3LYP/aug-cc-pVDZ optimized structures of tyrosine 1 and its two conjugate bases 2 and 3.²

Gas phase experiments indicate that deprotonation of tyrosine leads to a 70:30 mixture of the phenoxide to carboxylate anions. The computations are in nice agreement with this experiment. (A Boltzmann weighting of the computed lowest energy conformers makes only a small difference to the distribution relative to using simply the single lowest energy conformer.) This demonstrates once again the important role of solvent, since only the carboxylate anion is seen in aqueous solution.

References

(1) Tian, Z.; Pawlow, A.; Poutsma, J. C.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidity, H/D Exchange Experiments, and Computations on Cysteine and Its Conjugate Base," J. Am. Chem. Soc., 2007, 129, 5403-5407, DOI: 10.1021/ja0666194.

(2) Tian, Z.; Wang, X.-B.; Wang, L.-S.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidities, Photoelectron Spectra, and Computations on Tyrosine, p-Hydroxybenzoic Acid, and Their Conjugate Bases," J. Am. Chem. Soc., 2009, 131, 1174-1181, DOI: 10.1021/ja807982k.

InChIs

1: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/t8-/m0/s1/f/h12H
InChIKey=OUYCCCASQSFEME-QAXLLPJCDY

2: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/p-1/t8-/m0/s1/fC9H10NO3/q-1
InChIKey=OUYCCCASQSFEME-HVHKCMLZDU

3: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/p-1/t8-/m0/s1/fC9H10NO3/h11h,12H/q-1
InChIKey=OUYCCCASQSFEME-XGYCJDCADS