I missed this when it came out, but Quast, Sander and Borden have made the very interesting non-Kekule diradical 1.¹

³1

The EPR spectra shows the characteristic six-line signal, with zero-field splitting parameters consistent with related triplet diradicals. The Curie-Weiss plot is linear from 4.6 to 22.9 K. These data suggest a triplet ground state. CASSCF(14,14)/6-31G* computations indicate that the triplet lies 8.5 kcal mol^-1 below the singlet. The optimized triplet geometry is shown in Figure 1. The triplet ground state is consistent with the Borden-Davidson rules for radicals.²

31

Figure 1. CASSCF(14,14)/6-31G* optimized structure of triplet 1.

References

(1) Quast, H.; Nudling, W.; Klemm, G.; Kirschfeld, A.; Neuhaus, P.; Sander, W.; Hrovat, D. A.; Borden, W. T., "A Perimidine-Derived Non-Kekule Triplet Diradical," J. Org. Chem. 2008, 73, 4956-4961, DOI: 10.1021/jo800589y.

(2) Borden, W. T.; Davidson, E. R., "Effects of electron repulsion in conjugated hydrocarbon diradicals," J. Am. Chem. Soc. 1977, 99, 4587-4594, DOI: 10.1021/ja00456a010.

InChIs

1: InChI=1/C20H27N3/c1-19(2,3)13-8-12-9-14(20(4,5)6)11-16-17(12)15(10-13)22-18(21-7)23-16/h8-11H,1-7H3,(H2,21,22,23)/f/h22-23H
InChIKey=XAKUHDACNAUAAB-PDJAEHLQCL

Here’s another great example of synthesis of highly strained compounds. Bertrand has prepared the substituted triafulvalene 1.¹ The compound is stable as a solid or in solution under inert gas. It does however react quickly with water, a remarkable addition of water across an alkene. This is understood in terms of a very high HOMO and a low LUMO, indicating a very reactive double bond. The UV/Vis corroborates this: its absorption is at 502nm, compared to 171nm of ethylene and 217nm of 1,3-butadiene. The B3LYP/6-31G(d) structure of the tetraphenyl derivative 2 is shown in Figure 1.

1

2

Figure 1. B3LYP/6-31G(d) optimized structure of 2.

References

(1) Kinjo, R.; Ishida, Y.; Donnadieu, B.; Bertrand, G., "Isolation of Bicyclopropenylidenes: Derivatives of the Smallest Member of the Fulvalene Family," Angew. Chem. Int. Ed. 2009, 48, 517-520, DOI: 10.1002/anie.200804372

InChIs

1: InChIKey=GJHAFFXCMBMUNM-DBFBYELTBP

2: InChIKey=WTGGHSXPMAHUNP-UHFFFAOYAY

The nature of the bridgehead-bridgehead bond in [1.1.1]propellane 1 poses an interesting quandary. The bond involves two inverted carbon atoms, whose hybrids should point away from each other. The internuclear region has in fact much less electron density than for an ordinary C-C bond. Nonetheless, the molecule is stable and the C-C bond is estimated to have a strength of about 6 kcal mol^-1.

Shaik and Hiberty¹ have now proposed that the central C-C bond of [1.1.1]propellane is a charge-shift bond. In classical valence bond theory, we have three configurations for a bond: the covalent structure A↑↓B ↔ A↓↑B, and the two ionic structures A↑↓ B and A B↑↓. The description of a typical covalent bond is dominated by the covalent VB structure with a little bit of the ionic structures mixed in. A charge-shift bond is one where the resonance energy due to the mixing of the covalent and ionic structures mostly accounts for the stabilization of the bond.² Just such a case is found in the F-F bond, and also to for the central C-C bond of [1.1.1]propellane!

References

(1) Wu, W.; Gu, J.; Song, J.; Shaik, S.; Hiberty, P. C., "The Inverted Bond in [1.1.1]Propellane is a Charge-Shift Bond," Angew. Chem. Int. Ed., 2008, ASAP DOI: 10.1002/anie.200804965

(2) Shaik, S.; Danovich, D.; Silvi, B.; Lauvergnat, D. L.; Hiberty, P. C., "Charge-Shift Bonding – A Class of Electron-Pair Bonds That Emerges from Valence Bond Theory and Is Supported by the Electron Localization Function Approach," Chem. Eur. J., 2005, 11, 6358-6371, DOI: 10.1002/chem.200500265

InChI

1: InChI=1/C5H6/c1-4-2-5(1,4)3-4/h1-3H2
InChIKey=ZTXSPLGEGCABFL-UHFFFAOYAJ

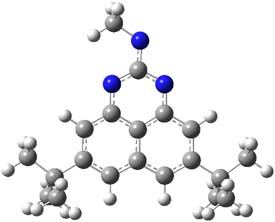
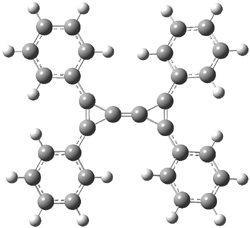
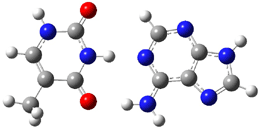
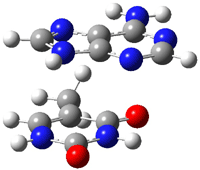
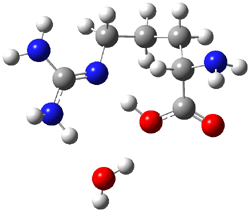
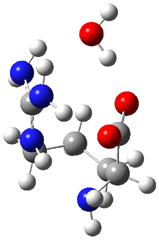
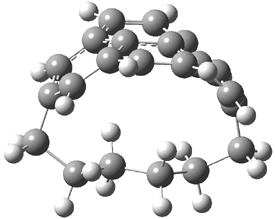
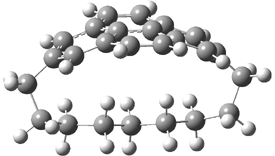
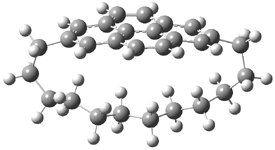
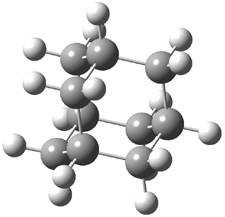
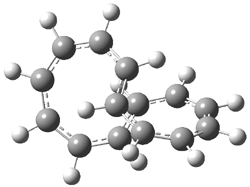
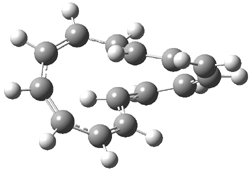
Here is another benchmark of the performance of DFT in handling difficult situations, in this case the interaction between nucleic acid base pairs. Sherrill¹ has examined the 124 nucleic acid base pairs from the JSCH-2005 database² compiled by Hobza and coworkers. This database includes 36 hydrogen bonded complexes, and example of which is shown in Figure 1a, and 54 stacked complex, one example of which is shown in Figure 1b.

(a)

(b)

Figure 1. Optimized geometries (RI-MP2/cc-pVTZ) of two representative structures of base pairs: (a) hydrogen bonded pair and (c) stacked pair.

The energies of these base pairs computed with four different functionals: PBE, PBE-D (where Grimme’s empirical dispersion correction³), and the recently developed MO5-2X⁴ and MO6-2X⁵ methods which attempt to treat mid-range electron correlation. The aug-cc-pVDZ basis set was used. These DFT energies are compared with the CCSD(T) energies of Hobza. The mean unsigned error (MUE) for the 28 hydrogen bonded complexes and the 54 stacked complexes are listed in Table 1.

Table 1. Mean unsigned error (kcal mol^-1) of the four DFT
methods (relative to CCSD(T)) for the hydrogen bonded and stacked base pairs.

A few interesting trends are readily apparent. First, PBE (representing standard GGA DFT methods) poorly describes the energy of the hydrogen bonded complexes, but utterly fails to treat the stacking interaction. Inclusion of the dispersion correction (PBE-D) results in excellent energies for the HB cases and quite reasonable results for the stacked pairs. Both of Truhlar’s functionals dramatically outperform PBE, though MO5-2X is probably still not appropriate for the stacked case. MO6-2X however seems to be a very reasonable functional for dealing with base pair interactions, indicating that mid-range correlation correction is sufficient to describe these complexes, and that the long-range correlation correction included in the dispersion correction, while giving improved results, is not essential.

References

(1) Hohenstein, E. G.; Chill, S. T.; Sherrill, C. D., "Assessment of the Performance of the M05-2X and M06-2X Exchange-Correlation Functionals for Noncovalent Interactions in Biomolecules," J. Chem. Theory Comput., 2008, 4, 1996-2000, DOI: 10.1021/ct800308k

(2) Jurecka, P.; Sponer, J.; Cerny, J.; P., H., "Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs," Phys. Chem. Chem. Phys., 2006, 8, 1985-1993, DOI: 10.1039/b600027d.

(3) Grimme, S., "Semiempirical GGA-type density functional constructed with a long-range dispersion correction," J. Comput. Chem., 2006, 27, 1787-1799, DOI: 10.1002/jcc.20495

(4) Zhao, Y.; Schultz, N. E.; Truhlar, D. G., "Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions," J. Chem. Theory Comput., 2006, 2, 364-382, DOI: 10.1021/ct0502763.

(5) Zhao, Y.; Truhlar, D. G., "The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals," Theor. Chem. Acc., 2008, 120, 215-241, DOI: 10.1007/s00214-007-0310-x.

The planar substituted cyclooctatetraene 1 has been prepared and characterized.¹ The B3LYP/6-31G(d) optimized geometry is shown in Figure 1.

1

Figure 1. B3LYP/6-31G(d) optimized geometry of 1.

The ¹H NMR spectrum of 1 shows the bridgehead proton has only a small upfield shift (Δδ = 0.18ppm) relative that of 2. This suggests that both molecules have similar degrees of aromaticity/antiaromaticity, and since both molecules display large bond alternation (ΔR = 0.169 Å in 1 and 0.089 Å in 2) one can argue that both paratropic and diatropic ring currents are attenuated in both molecules. However, the NICS value of 1 is 10.6 ppm, indicative of considerable antiaromatic character, though this NICS value is much reduced from that in planar cyclooctatetraene constrained to the ring geometry of 1 (22.1 ppm). Rabinowitz and Komatsu argue that large HOMO-LUMO gap of 1 is responsible for the reduced antiaromatic character of 1.

Though not discussed in their paper, the aromatic stabilization (destabilization) energy of 1 can be computed. I took two approaches, shown in Reactions 1 and 2. The energies of the two reactions are -13.8 kcal mol^-1 for Reaction 1 and -3.4 kcal mol^-1 for Reaction 2. The large exothermicity of Reaction 1 reflects the strain of packing the four bicyclo moieties near each other, forcing the neighboring bridgehead hydrogens to be directed right at each other. The strain is better compensated in Reaction 2 by using 3 as the reference. Since 3 is of C₂ symmetry, some strain relief remains a contributor to the overall reaction energy. Thus it appears that if 1 is antiaromatic, if manifests in little energetic consequence.

Reaction 1

Reaction 2

References

(1) Nishinaga, T.; Uto, T.; Inoue, R.; Matsuura, A.; Treitel, N.; Rabinovitz, M.; Komatsu, K., "Antiaromaticity and Reactivity of a Planar Cyclooctatetraene Fully Annelated with Bicyclo[2.1.1]hexane Units," Chem. Eur. J., 2008, 14, 2067-2074, DOI: 10.1002/chem.200701405

InChIs

1: InChI=1/C24H24/c1-9-2-10(1)18-17(9)19-11-3-13(4-11)21(19)23-15-7-16(8-15)24(23)22-14-5-12(6-14)20(18)22/h9-16H,1-8H2/b19-17-,20-18-,23-21-,24-22-
InChIKey=PUZMOHQGDBIGOO-LEYBOLSUBU

2: InChI=1/C18H18/c1-7-2-8(1)14-13(7)15-9-3-11(4-9)17(15)18-12-5-10(6-12)16(14)18/h7-12H,1-6H2
InChIKey=ULLLVKXTLZQQFF-UHFFFAOYAL

3: InChI=1/C14H16/c1-7-9-3-11(4-9)13(7)14-8(2)10-5-12(14)6-10/h9-12H,1-6H2/b14-13-
InChIKey=CSIHJUFBXMYVBH-YPKPFQOOBF

The gas phase structure of the amino acids is in their canonical or neutral form, while their aqueous solution phase structure is zwitterionic. An interesting question is how many water molecules are needed to make the zwitterionic structure more energetically favorable than the neutral form. For glycine, it appears that seven water molecules are needed to make the zwitterion the favorable tautomer.^1,2

Arginine, on the other hand, appears to require only one water molecule to make the zwitterion lower in energy than the neutral form.³ The B3LYP/6-311++G** structures of the lowest energy neutral (1N) and zwitterion (1Z) cluster with one water are shown in Figure 1. The zwitterion is 1.68 kcal mol^-1 lower in energy. What makes this zwitterion so favorable is that the protonation occurs on the guanidine group, not on the amine group. The guanidine group is more basic than the amine. Further, the water can accept a proton from both nitrogens of the guanidine and donate a proton to the carboxylate group.

1N (1.68)

1Z (0.0)

Figure 1. B3LYP/6-311++G** structures and relative energies (kcal mol^-1) of the lowest energy arginine neutral (1N) and zwitterion (1Z) cluster with one water.³

References

(1) Aikens, C. M.; Gordon, M. S., "Incremental Solvation of Nonionized and Zwitterionic Glycine," J. Am. Chem. Soc., 2006, 128, 12835-12850, DOI: 10.1021/ja062842p.

(2) Bachrach, S. M., "Microsolvation of Glycine: A DFT Study," j. Phys. Chem. A, 2008, 112, 3722-3730, DOI: 10.1021/jp711048c.

(3) Im, S.; Jang, S.-W.; Lee, S.; Lee, Y.; Kim, B., "Arginine Zwitterion is More Stable than the Canonical Form when Solvated by a Water Molecule," J. Phys. Chem. A, 2008, 112, 9767-9770, DOI: 10.1021/jp801933y.

InChIs

1: InChI=1/C6H14N4O2/c7-4(5(11)12)2-1-3-10-6(8)9/h4H,1-3,7H2,(H,11,12)(H4,8,9,10)/f/h8,10-11H,9H2
InChIKey=ODKSFYDXXFIFQN-MYOKTFMPCK

Once again into the breach – how much strain can an aromatic species withstand and remain aromatic? Cyranski, Bodwell and Schleyer employ the [n](2,7)pyrenophanes 1 to explore this question.¹ As the tethering bridge gets shorter, the pyrene framework must pucker, presumably reducing its aromatic character. Systematic shrinking allows one to examine the loss of aromaticity as defined by aromatic stabilization energy (ASE), magnetic susceptibility exaltation (Λ) and NICS, among other measures.

They examined the series of pyrenophanes where the tethering chain has 6 to 12 carbon atoms. I have shown the structures of three of these compounds in Figure 1. The bend angle α is defined as the angle made between the outside ring plane and the horizon. Relative ASE is computed using Reaction 1, which cleverly avoids the complication of exactly (a) what is the ASE of pyrene itself and (b) what is the strain energy in these compounds.

1a	1d
1g

Figure 1. B3LYP/6-311G** optimized geometries of 1a, 1d, and 1g.¹

Reaction 1

The results of the computations for this series of pyrenophanes is given in Table 1. The bending angle smoothly increases with decreasing length of the tether. The ASE decreases in the same manner. The ASE correlates quite well with the bending angle, as does the relative magnetic susceptibility exaltation. The NICS(1) values become less negative with decreasing tether length.

Table 1. Computed values for the pyrenophanes.

All of these trends are consistent with reduced aromaticity with increased out-of-plane distortion of the pyrene framework. What may be surprising is the relatively small loss of aromaticity in this sequence. Even though the bend angle is as large as almost 40°, the loss of ASE is only 16 kcal mol^-1, only about a quarter of the ASE of pyrene itself. Apparently, aromatic systems are fairly robust!

References

(1) Dobrowolski, M. A.; Cyranski, M. K.; Merner, B. L.; Bodwell, G. J.; Wu, J. I.; Schleyer, P. v. R.,
"Interplay of π-Electron Delocalization and Strain in [n](2,7)Pyrenophanes," J. Org. Chem., 2008, 73, 8001-8009, DOI: 10.1021/jo8014159

InChIs

1a: InChI=1/C22H20/c1-2-4-6-16-13-19-9-7-17-11-15(5-3-1)12-18-8-10-20(14-16)22(19)21(17)18/h7-14H,1-6H2
InChIKey=SJCYSWGQWCIONQ-UHFFFAOYAF

1b: InChI=1/C23H22/c1-2-4-6-16-12-18-8-10-20-14-17(7-5-3-1)15-21-11-9-19(13-16)22(18)23(20)21/h8-15H,1-7H2
InChIKey=VHVKAELFYUXZEM-UHFFFAOYAW

1c: InChI=1/C24H24/c1-2-4-6-8-18-15-21-11-9-19-13-17(7-5-3-1)14-20-10-12-22(16-18)24(21)23(19)20/h9-16H,1-8H2
InChIKey=HXPWDTNIUQNKLV-UHFFFAOYAQ

1d: InChI=1/C25H26/c1-2-4-6-8-18-14-20-10-12-22-16-19(9-7-5-3-1)17-23-13-11-21(15-18)24(20)25(22)23/h10-17H,1-9H2
InChIKey=DWYMZJZWMFVOIR-UHFFFAOYAM

1e: InChI=1/C26H28/c1-2-4-6-8-10-20-17-23-13-11-21-15-19(9-7-5-3-1)16-22-12-14-24(18-20)26(23)25(21)22/h11-18H,1-10H2
InChIKey=PZBADGOJPAEUIK-UHFFFAOYAZ

1f: InChI=1/C27H30/c1-2-4-6-8-10-20-16-22-12-14-24-18-21(11-9-7-5-3-1)19-25-15-13-23(17-20)26(22)27(24)25/h12-19H,1-11H2
InChIKey=YVZIXELCLJHDLW-UHFFFAOYAO

1g: InChI=1/C28H32/c1-2-4-6-8-10-12-22-19-25-15-13-23-17-21(11-9-7-5-3-1)18-24-14-16-26(20-22)28(25)27(23)24/h13-20H,1-12H2
InChIKey=QDAMLTATWKFTFB-UHFFFAOYAF

Pyrene: InChI=1/C16H10/c1-3-11-7-9-13-5-2-6-14-10-8-12(4-1)15(11)16(13)14/h1-10H
InChIKey=BBEAQIROQSPTKN-UHFFFAOYAB

4,9-dimethylenepyrene: InChI=1/C18H12/c1-11-9-13-5-4-8-16-12(2)10-14-6-3-7-15(11)17(14)18(13)16/h3-10H,1-2H2
InChIKey=XAAPFSHIUHWWCM-UHFFFAOYAM

There is a mystique surrounding chemical torture. Just how much strain can one subject a poor old carbon atom to? We construct such tortured molecules as cubane and cyclopentyne and trans-fused bicyclo[4.1.0]heptane. Inverted carbons – think of propellanes – are also a fruitful arena for torturing hydrocarbons. Now, Irikura has examined inverted adamantane inv-1.¹

The MP2/6-31G(d) optimized geometries of 1 and inv-1 and the transition state separating them are displayed in Figure 1. The inverted structure is a local energy minimum, lying 105 kcal mol^-1 above 1.² The barrier for rearrangement of the inverted adamantane into adamantane, which involved a cleave of a C-C bond, is 17 kcal mol^-1, which implies a half-life of 30 ms at 298K and and 2 days at 195 K. The perfluoro isomer has a higher barrier (32 kcal mol^-1) and a longer half-life (110 years at 298K).

1

TS-1

inv-1

Table 1. MP2/6-31G(d) optimized geometries of 1, inv-1, and the transition state connecting them.¹

So, inv-1 has some kinetic stability. It also has little computed reactivity with water, oxygen, or a second molecule of inv-1. Irikura, however, did not compute reactions that might lead to loss of a hydride from inv-1, which would give a non-classical cation.

As might be expected, the spectroscopic properties of inv-1 are unusual. The C-H vibrational
frequency for the inverted hydrogen is 3490 cm^-1 and the C-C-H bend is also 300 cm^-1 higher than in 1. The NMR shifts for the inverted methane group are 7.5 ppm for the hydrogen and 21 ppm for the carbon atom.

Irikura ends the article, “Experimental verification (or refutation) of [inv-1] presents a novel synthetic challenge.” Let’s hope someone picks up the gauntlet!

References

(1) Irikura, K. K., "In-Adamantane, a Small Inside-Out Molecule," J. Org. Chem. 2008, 73, 7906-7908, DOI: 10.1021/jo801806w.

(2) The energies are computed as E_estimate = E[CCSD(T)/6-31G(d)//MP2/6-31G(d)] + E[MP2/aug-cc-pVTZ//MP2/6-31G(d)] – E[MP2/6-31G(d)//MP2/6-31G(d)].

InChIs

1: InChI=1/C10H16/c1-7-2-9-4-8(1)5-10(3-7)6-9/h7-10H,1-6H2
InChIKey=ORILYTVJVMAKLC-UHFFFAOYAG

Rzepa has published another study of Möbius aromaticity.¹ Here he examines the [14]annulene 1 using the topological method (AIM) and NICS. The B3LYP/6-31G(d) optimized structures of 1, the transition state 3 and product of the 8-e^– electroclization 2 are shown in Figure 1.

1 (0.0)

3 (4.56)

2 (0.07)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energies (kcal mol^-1) of 1-3.¹

The topological analysis of 1 reveals a number of interesting features of the density. First, there are two bond critical points that connect the carbon atoms that cross over each other in the lemniscate structure 1 (these bond paths are drawn as the dashed lines in Scheme 1, connecting C₁ to C₈ and C₇ to C₁₄). These bond critical points have a much smaller electron density than for a typical C-C bond. With these added bond critical points come additional ring points, but not the anticipated 3 ring critical points. There is a ring critical point for the quasi-four member ring (C₁-C₁₄-C₇-C₈-C₁), but the expected ring point for each of the two 8-member ring bifurcate into two separate ring critical points sandwiching a cage critical point!

Scheme 1

Rzepa argues that the weak bonding interaction across the lemniscates is evidence for Möbius homoaromaticity in each half of 1. The NICS value at the central ring critical point is -18.6 ppm, reflective of overall Möbius aromaticity. But the NICS values at the 8-member ring ring critical points of -8.6 ppm and the cage critical points (-7.9 ppm) provide support for the Möbius homoaromaticity.

Transition state 3 corresponds to motion along the bond path of those weak bonds along either C₁-C₈ or C₇-C₁₄. This leads to forming the two fused eight-member rings of 2. An interesting thing to note is that there is only one transition state connecting 1 and 2 – even though one might think of the electrocyclization occurring in either the left or right ring. (Rzepa discusses this in a nice J. Chem. Ed. article.²) This transition state 3 is stabilized by Möbius aromaticity.

As an aside, Rzepa has once again made great use of the web in supplying a great deal of information through the web-enhanced object in the paper. As in the past, ACS continues to put this behind the subscriber firewall instead of considering it to be supporting material, which it most certainly is and should therefore be available to all.

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. AIM and ELF Critical Point and NICS Magnetic Analyses of Moöbius-Type Aromaticity and Homoaromaticity in Lemniscular Annulenes and Hexaphyrins," J. Org. Chem., 2008, 73, 6615-6622, DOI: 10.1021/jo801022b.

(2) Rzepa, H. S., "The Aromaticity of Pericyclic Reaction Transition States" J. Chem. Ed. 2007, 84, 1535-1540, http://www.jce.divched.org/Journal/Issues/2007/Sep/abs1535.html.

InChIs

1:
InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3-,6-4-,7-5+,8-6+,9-7-,10-8+,11-9-,12-10+,13-11-,14-12-,14-13-
InChIKey= RYQWRHUSMUEYST-YGYPEFQEBU

2: InChI=1/C14H14/c1-2-6-10-14-12-8-4-3-7-11-13(14)9-5-1/h1-14H/b2-1-,4-3-,9-5-,10-6-,11-7-,12-8-/t13-,14+
InChIKey= AMYHCQKNURYOBO-RFCQUTFOBS

Just how difficult can it be to compute rotational barriers? Well, it turns out that for biphenyl 1, the answer is “very”!

The experimental barriers for rotation about the C₁-C_1’ bond of biphenyl are 6.0 ± 2.1 kcal mol^-1 at 0° and 6.5 ± 2.0 kJ mol^-1 at 90°.¹ CCSD(T) with extrapolated basis set approximation computations by Sancho-Garcı´a and Cornil overestimate both barriers by more than 4 kJ mol^-1 and, more critically in error, predict that the 0° barrier is higher in energy than the 90° barrier.²

Now Johansson and Olsen have reported a comprehensive study of the rotational barrier of biphenyl.³ They tackled a number of different effects:

1. Basis sets: The cc-pVDZ basis set is simply too small to give any reasonable estimate (See Table 1).
2. Correlation effects: HF, MP2, SCS-MP2 and CCSD overestimate the barriers and get the relative energies of the two barriers wrong, regardless of the basis set. While CCSD(T) does properly predict the barrier at 0° is lower than that at 90°, even this level overestimates the barrier heights (Table 1).

Table 1. Computed torsional barriers in kJ mol^-1.

	MP2		CCSD(T)
	0°	90°	0°	90°
cc-pVDZ	12.23	7.68	10.89	7.23
aug-cc-pVDZ	9.68	7.45	9.23	6.67
cc-pVTZ	9.86	9.13	8.85	8.50
aug-cc-pVTZ	9.78	9.43	8.83	8.86
cc-pVQZ	9.65	9.33	8.68	8.74
aug-cc-pVQZ	9.35	9.31	8.39	8.76

3. Their best CCSD(T) energy using a procedure to extrapolate to infinite basis set still gives barriers that are too high, though in the right relative order: E(0°)=7.97 and E(90°) = 8.79 kJ mol^-1.
4. Inclusion of Core-Core and Core-Valence correlation energy reduces the 0° barrier and raises the 90° barrier a small amount. With an extrapolation for completeness in the coupled clusters expansion, their best estimates for the two barriers are 7.88 and 8.94 for the 0° and 90° barriers, respectively.
5. Relativity has no effect on the barrier heights. (This is a great result – it suggests that we don’t have to worry about relativistic corrections for normal organics!)
6. Intramolecular basis set superposition error might be responsible for as much a 0.4 kJ difference in the energies of the two barriers.
7. Inclusion of vibrational energies along with all of the other corrections listed above leads to their best estimate of the two barriers: E(0°)=8.0 and E(90°) = 8.3 kJ mol^-1, which are at least in the correct order and within the experimental error bars.

Who would have thought this problem was so difficult?

References

(1) Bastiansen, O.; Samdal, S., "Structure and barrier of internal rotation of biphenyl derivatives in the gaseous state: Part 4. Barrier of internal rotation in biphenyl, perdeuterated biphenyl and seven non-ortho-substituted halogen derivatives," J. Mol. Struct., 1985, 128, 115-125, DOI: 10.1016/0022-2860(85)85044-4.

(2) Sancho-Garcia, J. C.; Cornil, J., "Anchoring the Torsional Potential of Biphenyl at the ab Initio Level: The Role of Basis Set versus Correlation Effects," J. Chem. Theory Comput., 2005, 1, 581-589, DOI: 10.1021/ct0500242.

(3) Johansson, M. P.; Olsen, J., "Torsional Barriers and Equilibrium Angle of Biphenyl: Reconciling Theory with Experiment," J. Chem. Theory Comput., 2008, 4, 1460-1471, DOI: 10.1021/ct800182e.

InChIs

Biphenyl 1: InChI=1/C12H10/c1-3-7-11(8-4-1)12-9-5-2-6-10-12/h1-10H
InChIKey: ZUOUZKKEUPVFJK-UHFFFAOYAV