What is the size of a molecule that will stretch computational resources today? Chan and co-workers have examined some very large fullerenes1 to both answer that question, and also to explore how large a fullerene must be to approach graphene-like properties.
They are interested in predicting the heat of formation of large fullerenes. So, they benchmark the heats of formation of C60 using four different isodesmic reactions (Reaction 1-4), comparing the energies obtained using a variety of different methods and basis sets to those obtained at W1h. The methods include traditional functionals like B3LYP, B3PW91, CAM-B3LYP, PBE1PBE, TPSSh, B98, ωB97X, M06-2X3, and MN12-SX, and supplement them with the D3 dispersion correction. Additionally a number of doubly hybrid methods are tested (again with and without dispersion corrections), such as B2-PLYP, B2GPPLYP, B2K-PLYP, PWP-B95, DSD-PBEPBE, and DSD-B-P86. The cc-pVTZ and cc-pVQZ basis sets were used. Geometries were optimized at B3LYP/6-31G(2df,p).
|
C60 + 10 benzene → 6 corannulene |
Reaction 1 |
|
C60 + 10 naphthalene → 8 corannulene |
Reaction 2 |
|
C60 + 10 phenanthrene → 10 corannulene |
Reaction 3 |
|
C60 + 10 triphenylene → 12 corannulene |
Reaction 4 |
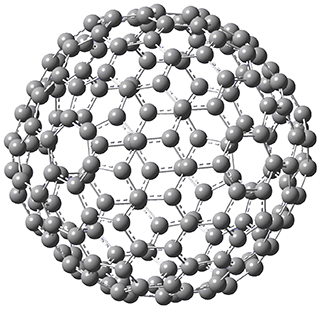
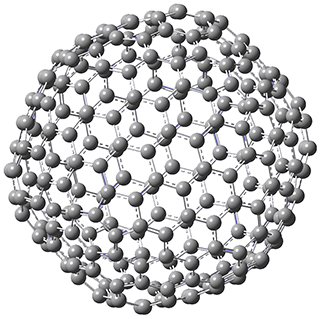
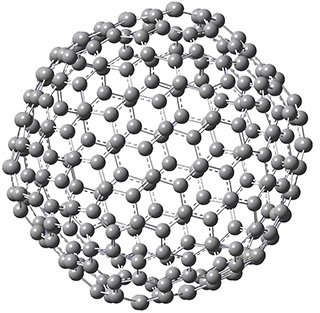
Excellent results were obtained with DSD-PBEPBE-D3/cc-pVQZ (an error of only 1.8 kJ/mol), though even a method like BMK-D3/cc-pVTZ had an error of only 9.2 kJ/mol. They next set out to examine large fullerenes, including such behemoths as C180, C240, and C320, whose geometries are shown in Figure 1. Heats of formation were obtained using isodesmic reactions that compare back to smaller fullerenes, such as in Reaction 5-8.
|
C70 + 5 styrene → C60 + 5 naphthalene |
Reaction 5 |
|
C180 → 3 C60 |
Reaction 6 |
|
C320 + 2/3 C60 → 2 C180 |
Reaction 7 |
|
C180 |
|
C240 |
|
C320 |
Figure 1. B3LYP/6-31G(2df,p) optimized geometries of C180, C240, and C320. (Don’t forget that clicking on these images will launch Jmol and allow you to manipulate the molecules in real-time.)
Next, taking the heat of formation per C for these fullerenes, using a power law relationship, they were able to extrapolate out the heat of formation per C for truly huge fullerenes, and find the truly massive fullerenes, like C9680, still have heats of formation per carbon 1 kJ/mol greater than for graphene itself.
References
(1) Chan, B.; Kawashima, Y.; Katouda, M.; Nakajima, T.; Hirao, K. "From C60 to Infinity: Large-Scale Quantum Chemistry Calculations of the Heats of Formation of Higher Fullerenes," J. Am. Chem. Soc. 2016, 138, 1420-1429, DOI: 10.1021/jacs.5b12518.

Henry Rzepa responded on 29 Feb 2016 at 2:56 am #
Re: “What is the size of a molecule that will stretch computational resources today? ”
C320 is certainly impressive, but as a practical matter, what can we infer from this?
Thus the single two most important aspects of deciding if you have enough resources to perform any given calculation is
1. How many processors in parallel you can deploy and
2. How much shared memory can you allocate to the run.
Thus, even a few years ago, GAMESS was capable of running >1000 processors in parallel for certain types of calculation, but I suspect more typically on the sorts of commodity systems out there and the typical software used, the more realistic number is 8-64 (please correct me if you think it is outside of these limits) and the average commodity memory is probably < 100 Gbyte.
I set out to find from the article above what sort of resources had been used for their research. It is not quoted (unless I missed it) in either the body of the article or its SI. Part of the problem is that SI almost always is condensed down from the actual outputs (mostly just to the coordinates). What is almost always missing is
3. The input conditions, including keyword/value pairs defining various run settings, convergence limits, etc etc.
4. The actual outputs, which contain far more information about the run itself. This often includes how many processors and memory was used and the actual wall times of the runs themselves (important if your batch queues have time limit constraints).
This sort of information is key to answering questions such as “What is the size of a molecule that my own computational resources today can stretch to?”
I must again make the point that SI is no longer (if it ever was) fit for purpose in its current form and that the general area of RDM (research data management) sets out many guidelines for making research data available. One aspect of this is to help researchers easily answer questions about resources such as above.
If you are about to attend the ACS national meeting in San Diego, there are several sessions devoted to these general topics, e.g. https://ep70.eventpilotadmin.com/web/page.php?page=Session&project=ACS16spring&id=208680 and I urge you to attend some of them!
Fabio Pichierri responded on 03 Mar 2016 at 2:30 am #
Henry,
I fully agree with you that information on the nr. of processors and shared memory is key to answering the above question. As far as I know, performances are linear in the range 2-X processors, non-linear in the range X-Y processors and then saturation occurs above Y processors for most quantum chemistry packages. Hence, the performance-processors dependence is important for defining the size of the molecule that can be treated with a specific resource/computer.
Steven Bachrach responded on 03 Mar 2016 at 8:55 am #
There are certainly lots of factors that play into answering the question “what is the size of a molecule that will stretch computational resources today?” The number of processors, the speed of these processors, the amount of RAM, the amount of disk, symmetry, qm method, basis set size, etc. I asked this question not to give a specific answer, but rather to to step back and think about how far we have come in terms of the size of the molecule that we can routinely handle.
Fabio Pichierri responded on 04 Mar 2016 at 3:15 pm #
Steven,
indeed, it is important to think about the above question but does routine handling include or not the use of supercomputers? I am asking this question because routine calculations are usually performed on workstations which are available in most labs.