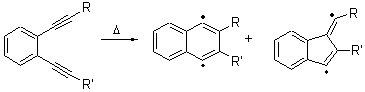
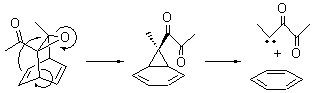
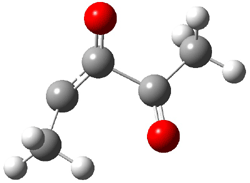
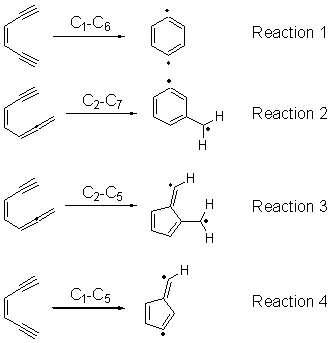
Cyclization of enediynes is thoroughly discussed in Chapter 3.3 of my book. The reaction that started all the excitement is the C₁-C₆ cyclization (the Bergman cyclization, Reaction 1). Meyers and Saito then proposed the alternative C₂-C₇ cyclization (Reaction 2), and a variant on this, the Schmittel cyclization (Reaction 3) followed soon thereafter. Now, Pascal completes the theme with a report on the C₁-C₅ cyclization (Reaction 4).¹

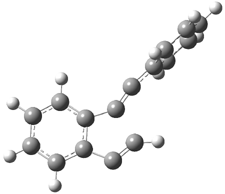
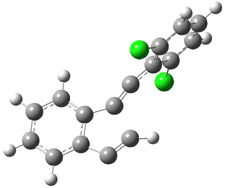
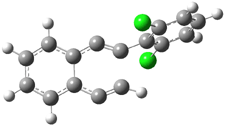
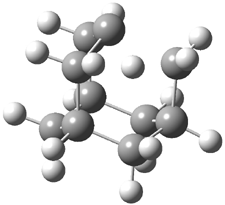
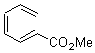
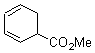
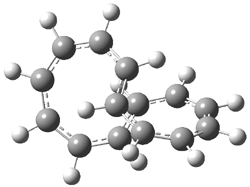
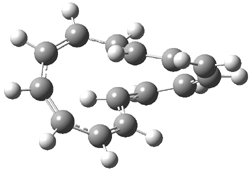
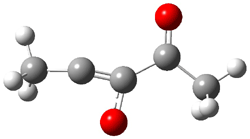
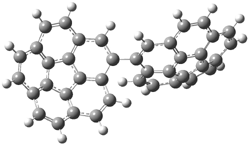
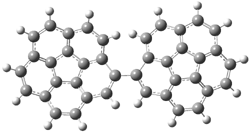
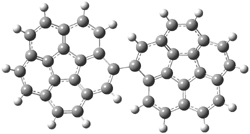
Pascal begins with the assumption that terminal aryl substitution on the enediyne will both (a) inhibit the C₁-C₆ cyclization due to steric interactions and (b) the C₁-C₅ cyclization should be enhanced due to stabilization of the radical by the neighboring aryl group. He computed the activation energies of a series of analogues, some of which are listed in Table 1. The transition state structures are shown in Figure 1 for 1b and 1c. Phenyl substitution does accomplish both suggestions: the activation barrier for the Bergman cyclization increases by 4 kcal mol^-1, while the barrier for the C₁-C₅ cyclization is lowered by nearly 6 kcal mol^-1. Further substitution of the phenyl ring by either chloro or methyl groups brings the barriers into near degeneracy.

Table 1. RBLYP/6-31G(d) Activation energies (kcal mol^-1) for
competing cyclization reactions of substituted enediynes.¹

C1-C5 TS of 1b	C1-C6 TS of 1b
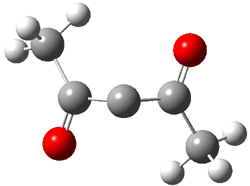
C1-C5 TS of 1c	C1-C6 TS of 1c

Figure 1. RBLYP/6-31G(d) optimized geometries of the C₁-C₅ and C₁-C₆ transition states for 1b and 1c.¹

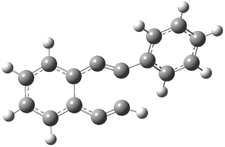
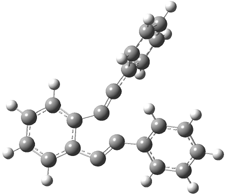
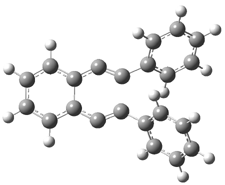
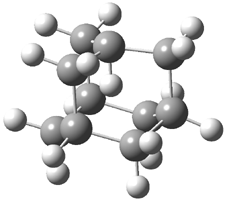
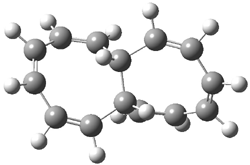
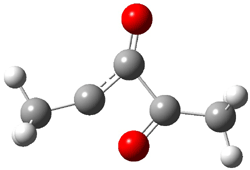
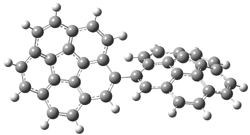
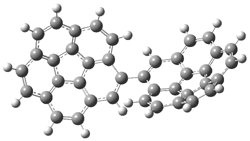
The di-substituted enediynes were examined next. The C₁-C₅ and C₁-C₆ transition states for the phenyl (2a) analogue are shown in Figure 2, and the activation energies for it and the 2,4,6-trichlorophenyl (2b) analogue are listed in Table 1. With BLYP, the C₁-C₅ cyclization is favored by a significant amount over the Bergman cyclization. This may be an overestimation as the BCCD(T)/cc-pVDZ//-BLYP/6-31G(d) computations predict the opposite energy ordering.

C1-C5 TS of 2a

C1-C2 TS of 2a

Figure 1. RBLYP/6-31G(d) optimized geometries of the C₁-C₅ and C₁-C₆ transition states for 2a.¹

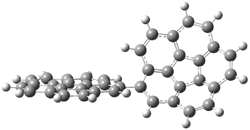
Pascal synthesized 2b and subjected it to thermolysis. Only indenes were obtained, indicative of the C₁-C₅ cyclization occurring in total preference over the C₁-C₆ pathway. The presence of 1,4-cyclohexadiene does improve the yields, suggestive that the transfer hydrogenation mechanism may be operative. However, when the reaction is done in the absence of 1,4-cyclohexadiene and at lower temperature (180 °C), the C₁-C₅ cyclization is still observed and no Bergman cyclization is seen. It appears that C₁-C₅ cyclization of enediynes is a viable reaction.

References

(1) Vavilala, C.; Byrne, N.; Kraml, C. M.; Ho, D. M.; Pascal, R. A., "Thermal C¹-C⁵ Diradical Cyclization of Enediynes," J. Am. Chem. Soc. 2008, 130, 13549-13551, DOI: 10.1021/ja803413f.

InChIs

1a: InChI=1/C10H6/c1-3-9-7-5-6-8-10(9)4-2/h1-2,5-8H
InChIKey=CBYDUPRWILCUIC-UHFFFAOYAY

1b: InChI=1/C16H10/c1-2-15-10-6-7-11-16(15)13-12-14-8-4-3-5-9-14/h1,3-11H
InChIKey=FFEGFMOHMPSHTK-UHFFFAOYAQ

1c: InChI=1/C16H8Cl2/c1-2-12-6-3-4-7-13(12)10-11-14-15(17)8-5-9-16(14)18/h1,3-9H
InChIKey=ZQRAACNBGPDESE-UHFFFAOYAV

1d: InChI=1/C18H14/c1-4-16-10-5-6-11-17(16)12-13-18-14(2)8-7-9-15(18)3/h1,5-11H,2-3H3
InChIKey=XGUCEMJKUJLOHZ-UHFFFAOYAZ

2a: InChI=1/C22H14/c1-3-9-19(10-4-1)15-17-21-13-7-8-14-22(21)18-16-20-11-5-2-6-12-20/h1-14H
InChIKey=XOJSMLDMLXWRMT-UHFFFAOYAD

2b: InChI=1/C22H8Cl6/c23-15-9-19(25)17(20(26)10-15)7-5-13-3-1-2-4-14(13)6-8-18-21(27)11-16(24)12-22(18)28/h1-4,9-12H
InChIKey=FNGRRGHMCFPDDG-UHFFFAOYAU

There is a mystique surrounding chemical torture. Just how much strain can one subject a poor old carbon atom to? We construct such tortured molecules as cubane and cyclopentyne and trans-fused bicyclo[4.1.0]heptane. Inverted carbons – think of propellanes – are also a fruitful arena for torturing hydrocarbons. Now, Irikura has examined inverted adamantane inv-1.¹

The MP2/6-31G(d) optimized geometries of 1 and inv-1 and the transition state separating them are displayed in Figure 1. The inverted structure is a local energy minimum, lying 105 kcal mol^-1 above 1.² The barrier for rearrangement of the inverted adamantane into adamantane, which involved a cleave of a C-C bond, is 17 kcal mol^-1, which implies a half-life of 30 ms at 298K and and 2 days at 195 K. The perfluoro isomer has a higher barrier (32 kcal mol^-1) and a longer half-life (110 years at 298K).

1

TS-1

inv-1

Table 1. MP2/6-31G(d) optimized geometries of 1, inv-1, and the transition state connecting them.¹

So, inv-1 has some kinetic stability. It also has little computed reactivity with water, oxygen, or a second molecule of inv-1. Irikura, however, did not compute reactions that might lead to loss of a hydride from inv-1, which would give a non-classical cation.

As might be expected, the spectroscopic properties of inv-1 are unusual. The C-H vibrational
frequency for the inverted hydrogen is 3490 cm^-1 and the C-C-H bend is also 300 cm^-1 higher than in 1. The NMR shifts for the inverted methane group are 7.5 ppm for the hydrogen and 21 ppm for the carbon atom.

Irikura ends the article, “Experimental verification (or refutation) of [inv-1] presents a novel synthetic challenge.” Let’s hope someone picks up the gauntlet!

References

(1) Irikura, K. K., "In-Adamantane, a Small Inside-Out Molecule," J. Org. Chem. 2008, 73, 7906-7908, DOI: 10.1021/jo801806w.

(2) The energies are computed as E_estimate = E[CCSD(T)/6-31G(d)//MP2/6-31G(d)] + E[MP2/aug-cc-pVTZ//MP2/6-31G(d)] – E[MP2/6-31G(d)//MP2/6-31G(d)].

InChIs

1: InChI=1/C10H16/c1-7-2-9-4-8(1)5-10(3-7)6-9/h7-10H,1-6H2
InChIKey=ORILYTVJVMAKLC-UHFFFAOYAG

While catalysis of many pericyclic reactions have been reported, until now there have been no reports of a catalyzed electrocylization. Bergman, Trauner and coworkers have now identified the use of an aluminum Lewis Acid to catalyze a 6e^– electrocyclization.¹

They start off by noting that electron withdrawing groups on the C₂ position of a triene lowers the barrier of the electrocylization. So they model the carbomethoxy substituted hexatriene (1a-d) with a proton attached to the carbonyl oxygen as the Lewis acid at B3LYP/6-31G**. Table 1 presents the barrier for the four possible isomeric reactions. Only in the case where the substituent is in the 2 position is there a significant reduction in the activation barrier: 10 kcal mol^-1.

Table 1. B3LYP/6-31G** activation barriers (kcal mol^-1) for the catalyzed (H⁺) and uncatalyzed electrocylication reaction of carbomethoxy-substituted hexatrienes.

With these calculations as a guide, they synthesized compounds 3 and 5 and used Me₂AlCl as the catalysts. In both cases, significant rate enhancement was observed. The thermodynamic parameters for these electrocylizations are given in Table 2. The aluminum catalyst acts primarily to lower the enthalpic barrier, as predicted by the DFT computations. The effect is not as dramatic as for the computations due likely to a much greater charge dispersal in over the aluminum catalyst (as opposed to the tiny proton in the computations) and the omission of solvent from the calculations.

Table 2. Experimental thermodynamic parameters for the electrocylcization of 3 and 5.

References

(1) Bishop, L. M.; Barbarow, J. E.; Bergman, R. G.; Trauner, D., "Catalysis of 6π Electrocyclizations," Angew. Chem. Int. Ed. 2008, 47, 8100-8103, DOI: 10.1002/anie.200803336

InChIs

1a: InChI=1/C8H10O2/c1-3-4-5-6-7-8(9)10-2/h3-7H,1H2,2H3/b5-4-,7-6+
InChIKey=INMLJEKOJCNLTL-SCFJQAPRBY

1b: InChI=1/C8H10O2/c1-3-4-5-6-7-8(9)10-2/h3-7H,1H2,2H3/b5-4-,7-6-
InChIKey=INMLJEKOJCNLTL-RZSVFLSABV

1c: InChI=1/C8H10O2/c1-4-5-6-7(2)8(9)10-3/h4-6H,1-2H2,3H3/b6-5-
InChIKey=QALYADPPGKOFPQ-WAYWQWQTBX

1d: InChI=1/C8H10O2/c1-4-6-7(5-2)8(9)10-3/h4-6H,1-2H2,3H3/b7-6+
InChIKey=BRDQFYBEWWPLFX-VOTSOKGWBR

2a: InChI=1/C8H10O2/c1-10-8(9)7-5-3-2-4-6-7/h2-5>,7H,6H2,1H3
InChIKey=LUFUPKXCMNRVLT-UHFFFAOYAU

2c: InChI=1/C8H10O2/c1-10-8(9)7-5-3-2-4-6-7/h2-3,5H,4,6H2,1H3
InChIKey=KPYYGHDMWKXJCE-UHFFFAOYAC

2d: InChI=1/C8H10O2/c1-10-8(9)7-5-3-2-4-6-7/h3,5-6H,2,4H2,1H3
InChIKey=YCTXQIVXFOMZCV-UHFFFAOYAU

3: InChI=1/C17H20O2/c1-5-16(17(18)19-4)14(3)11-13(2)12-15-9-7-6-8-10-15/h5-12H,1-4H3/b13-12+,14-11-,16-5-
InChIKey=DPBZDJWWRAWHQX-USTKDYFJBV

4: InChI=1/C17H20O2/c1-11-10-12(2)16(17(18)19-4)13(3)15(11)14-8-6-5-7-9-14/h5-10,13,15H,1-4H3/t13-,15-/m1/s1
InChIKey=JFBDOBRQORXZEY-UKRRQHHQBP

5: InChI=1/C16H16O/c1-13(12-14-6-3-2-4-7-14)10-11-15-8-5-9-16(15)17/h2-4,6-8,10-12H,5,9H2,1H3/b11-10-,13-12+
InChIKey=OAQIPONHGIZOBU-JPYSRSMKBG

6: InChI=1/C16H16O/c1-11-7-8-13-14(9-10-15(13)17)16(11)12-5-3-2-4-6-12/h2-8,14,16H,9-10H2,1H3/t14-,16-/m0/s1
InChIKey=MJUGKTLVECDOOO-HOCLYGCPBO

Rzepa has published another study of Möbius aromaticity.¹ Here he examines the [14]annulene 1 using the topological method (AIM) and NICS. The B3LYP/6-31G(d) optimized structures of 1, the transition state 3 and product of the 8-e^– electroclization 2 are shown in Figure 1.

1 (0.0)

3 (4.56)

2 (0.07)

Figure 1. B3LYP/6-31G(d) optimized structures and relative energies (kcal mol^-1) of 1-3.¹

The topological analysis of 1 reveals a number of interesting features of the density. First, there are two bond critical points that connect the carbon atoms that cross over each other in the lemniscate structure 1 (these bond paths are drawn as the dashed lines in Scheme 1, connecting C₁ to C₈ and C₇ to C₁₄). These bond critical points have a much smaller electron density than for a typical C-C bond. With these added bond critical points come additional ring points, but not the anticipated 3 ring critical points. There is a ring critical point for the quasi-four member ring (C₁-C₁₄-C₇-C₈-C₁), but the expected ring point for each of the two 8-member ring bifurcate into two separate ring critical points sandwiching a cage critical point!

Scheme 1

Rzepa argues that the weak bonding interaction across the lemniscates is evidence for Möbius homoaromaticity in each half of 1. The NICS value at the central ring critical point is -18.6 ppm, reflective of overall Möbius aromaticity. But the NICS values at the 8-member ring ring critical points of -8.6 ppm and the cage critical points (-7.9 ppm) provide support for the Möbius homoaromaticity.

Transition state 3 corresponds to motion along the bond path of those weak bonds along either C₁-C₈ or C₇-C₁₄. This leads to forming the two fused eight-member rings of 2. An interesting thing to note is that there is only one transition state connecting 1 and 2 – even though one might think of the electrocyclization occurring in either the left or right ring. (Rzepa discusses this in a nice J. Chem. Ed. article.²) This transition state 3 is stabilized by Möbius aromaticity.

As an aside, Rzepa has once again made great use of the web in supplying a great deal of information through the web-enhanced object in the paper. As in the past, ACS continues to put this behind the subscriber firewall instead of considering it to be supporting material, which it most certainly is and should therefore be available to all.

References

(1) Allan, C. S. M.; Rzepa, H. S., "Chiral Aromaticities. AIM and ELF Critical Point and NICS Magnetic Analyses of Moöbius-Type Aromaticity and Homoaromaticity in Lemniscular Annulenes and Hexaphyrins," J. Org. Chem., 2008, 73, 6615-6622, DOI: 10.1021/jo801022b.

(2) Rzepa, H. S., "The Aromaticity of Pericyclic Reaction Transition States" J. Chem. Ed. 2007, 84, 1535-1540, http://www.jce.divched.org/Journal/Issues/2007/Sep/abs1535.html.

InChIs

1:
InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3-,6-4-,7-5+,8-6+,9-7-,10-8+,11-9-,12-10+,13-11-,14-12-,14-13-
InChIKey= RYQWRHUSMUEYST-YGYPEFQEBU

2: InChI=1/C14H14/c1-2-6-10-14-12-8-4-3-7-11-13(14)9-5-1/h1-14H/b2-1-,4-3-,9-5-,10-6-,11-7-,12-8-/t13-,14+
InChIKey= AMYHCQKNURYOBO-RFCQUTFOBS

Cramer and Truhlar have tested their latest solvation model SM8 against a test set of 17 small, drug-like molecules.¹ Their best result comes with the use of SM8, the MO5-2X functional, the 6-31G(d) basis set and CM4M charge model. This computational model yields a root mean squared error for the solvation free energy of 1.08 kcal mol^-1 across this test set. This is the first time these authors have recommended a particular computational model. Another interesting point is that use of solution-phase optimized geometries instead of gas-phase geometries leads to only marginally improved solvation energies, so that the more cost effective use of gas-phase structures is encouraged.

These authors note in conclusion that further improvement of solvation prediction rests upon “an infusion of new experimental data for molecules characterized by high degrees of functionality (i.e. druglike)”.

References

(1) Chamberlin, A. C.; Cramer, C. J.; Truhlar, D. G., “Performance of SM8 on a Test To Predict Small-Molecule Solvation Free Energies,” J. Phys. Chem. B, 2008, 112, 8651-8655, DOI: 10.1021/jp8028038.

Just how difficult can it be to compute rotational barriers? Well, it turns out that for biphenyl 1, the answer is “very”!

The experimental barriers for rotation about the C₁-C_1’ bond of biphenyl are 6.0 ± 2.1 kcal mol^-1 at 0° and 6.5 ± 2.0 kJ mol^-1 at 90°.¹ CCSD(T) with extrapolated basis set approximation computations by Sancho-Garcı´a and Cornil overestimate both barriers by more than 4 kJ mol^-1 and, more critically in error, predict that the 0° barrier is higher in energy than the 90° barrier.²

Now Johansson and Olsen have reported a comprehensive study of the rotational barrier of biphenyl.³ They tackled a number of different effects:

1. Basis sets: The cc-pVDZ basis set is simply too small to give any reasonable estimate (See Table 1).
2. Correlation effects: HF, MP2, SCS-MP2 and CCSD overestimate the barriers and get the relative energies of the two barriers wrong, regardless of the basis set. While CCSD(T) does properly predict the barrier at 0° is lower than that at 90°, even this level overestimates the barrier heights (Table 1).

Table 1. Computed torsional barriers in kJ mol^-1.

	MP2		CCSD(T)
	0°	90°	0°	90°
cc-pVDZ	12.23	7.68	10.89	7.23
aug-cc-pVDZ	9.68	7.45	9.23	6.67
cc-pVTZ	9.86	9.13	8.85	8.50
aug-cc-pVTZ	9.78	9.43	8.83	8.86
cc-pVQZ	9.65	9.33	8.68	8.74
aug-cc-pVQZ	9.35	9.31	8.39	8.76

3. Their best CCSD(T) energy using a procedure to extrapolate to infinite basis set still gives barriers that are too high, though in the right relative order: E(0°)=7.97 and E(90°) = 8.79 kJ mol^-1.
4. Inclusion of Core-Core and Core-Valence correlation energy reduces the 0° barrier and raises the 90° barrier a small amount. With an extrapolation for completeness in the coupled clusters expansion, their best estimates for the two barriers are 7.88 and 8.94 for the 0° and 90° barriers, respectively.
5. Relativity has no effect on the barrier heights. (This is a great result – it suggests that we don’t have to worry about relativistic corrections for normal organics!)
6. Intramolecular basis set superposition error might be responsible for as much a 0.4 kJ difference in the energies of the two barriers.
7. Inclusion of vibrational energies along with all of the other corrections listed above leads to their best estimate of the two barriers: E(0°)=8.0 and E(90°) = 8.3 kJ mol^-1, which are at least in the correct order and within the experimental error bars.

Who would have thought this problem was so difficult?

References

(1) Bastiansen, O.; Samdal, S., "Structure and barrier of internal rotation of biphenyl derivatives in the gaseous state: Part 4. Barrier of internal rotation in biphenyl, perdeuterated biphenyl and seven non-ortho-substituted halogen derivatives," J. Mol. Struct., 1985, 128, 115-125, DOI: 10.1016/0022-2860(85)85044-4.

(2) Sancho-Garcia, J. C.; Cornil, J., "Anchoring the Torsional Potential of Biphenyl at the ab Initio Level: The Role of Basis Set versus Correlation Effects," J. Chem. Theory Comput., 2005, 1, 581-589, DOI: 10.1021/ct0500242.

(3) Johansson, M. P.; Olsen, J., "Torsional Barriers and Equilibrium Angle of Biphenyl: Reconciling Theory with Experiment," J. Chem. Theory Comput., 2008, 4, 1460-1471, DOI: 10.1021/ct800182e.

InChIs

Biphenyl 1: InChI=1/C12H10/c1-3-7-11(8-4-1)12-9-5-2-6-10-12/h1-10H
InChIKey: ZUOUZKKEUPVFJK-UHFFFAOYAV

Following on the great study of hydroxycarbene¹ (see my blog post), Schreiner now reports on the synthesis and characterization of dihydroxycarbene 1.² It is prepared by high-vacuum flash pyrolysis of oxalic acid (Scheme 1).

Scheme 1

Dihydroxycarbene can exist in three different conformations characterized by the relationship about the C-O bond, either s-cis or s-trans. The three conformations are shown in Figure 1, and the s-trans,s-trans structure is the local energy minimum (computed at CCSD(T)/cc-pVTZ).

1tt (0.0)

1ct (0.1)

1cc (6.7)

Figure 1. CCSD(T)/cc-pVTZ optimized geometries and relative energies (kcal mol^-1) of the conformers of 1.²

Identification of the 1 is made through comparison of the experimental and computed IR vibrational frequencies. As an example, the experimental and computed frequencies for the s-trans,s-trans conformer are listed in Table 1. The agreement is excellent.

Table 1. Computed and experimental vibrational frequencies (cm^-1) and intensities (in parentheses) of the s-trans,s-trans conformation of 1.²

Unlike hydroxycarbene, dihydroxycarbene is stable. The amazing instability of hydroxycarbene is due to tunneling through a large barrier: nearly 30 kcal mol^-1.¹ The tunneling route for the decomposition of 1 is more difficult for two reasons. First, its C-O bond is quite strong; the C-O distance is quite short, 1.325 Å. This makes a long distance that must be traversed in the tunneling mode. (The strong bond is due to π-donation from the oxygen lone pair into the empty carbon p orbital; this is noted by the large rotational barrier about the C-O bonds of 17 kcal mol^-1!) Second, the activation barrier for decomposition is very high, at least 34 kcal mol^-1.

References

(1) Schreiner, P. R.; Reisenauer, H. P.; Pickard Iv, F. C.; Simmonett, A. C.; Allen, W. D.; Matyus, E.; Csaszar, A. G., "Capture of hydroxymethylene and its fast disappearance through tunnelling," Nature, 2008, 453, 906-909, DOI: 10.1038/nature07010.

(2) Schreiner, P. R.; Reisenauer, H. P., "Spectroscopic Identification of Dihydroxycarbene13," Angew. Chem. Int. Ed., 2008, 47, 7071-7074, DOI: 10.1002/anie.200802105

InChIs

1: InChI=1/CH2O2/c2-1-3/h2-3H

Well, here’s my vote for paper of the year (at least so far!). It is work from Barry Carpenter’s lab¹ and pertains to many topics discussed in my book, including pericyclic and psuedopericylic reactions, non-statistical dynamics, and the use of high-level computations to help understand confusing experimental results. The paper is in an interesting read – and not just for the great science. It is told as a story, recounting the experiments and interpretation as they took place in chronological order with a surprising and critical contribution made from a referee!

The story begins with Carpenter’s continuing interest in unusual dynamic effects and the supposition that non-statistical dynamics might be observed in the rearrangements of carbenes. So, they took on the Wolff rearrangement, specifically the rearrangement of 3 into 4. Using labeled starting material 1, one should observe equal amounts of 4a and 4b if normal statistical dynamics is occurring (Scheme 1).

Scheme 1.

In fact, the ratio of products is not unity, but rather 4a:4b = 1:4.5. But the excess of 4b could be the result of another parallel rearrangement, 2 to 5 to 4b (Scheme 2).

Scheme 2.

To try to distinguish whether 5 is intervening, they carried out the photolysis of a different labeled version of 1 (namely 1’). The product distribution of the products is shown in Sheme 3. It appears that the reaction through 5 dominates, but the ratio of products that come from 3 still shows non-statistical behavior.

Scheme 3.

CCSD(T) computation suggested that 5 is higher in energy than 3, and this does not help understand the experiments. At this point, Carpenter decided to write up the work as a communication, with the main point that non-statistical dynamics were occurring.

Now here an unusual event took place that offers up hope that the peer-review system still works! A referee, later identified as Dan Singleton, offered an alternative mechanism for the production of 5. Shown in Scheme 4 is the novel pseudopericylic reaction that leads from 1 directly to 5. In fact, the transition state for this pseudopericyclic reaction is 19.0 kcal mol^-1 lower in energy than the transition state for the retro-Diels-Alder reaction of Scheme 1 (computed at MPWB1K/ 6-31+G(d,p), and this pseudopericyclic TS is shown in Figure 1).

Scheme 4.

Figure 1. MPWB1K/6-31+G(d,p) optimized geometry of the transition state for the pseudopericyclic reaction shown in Scheme 4.¹

The revised mechanism was then modified to include the additional complication of the formation of 6, and is shown in Scheme 5, along with their relative CCSD(T) energies. The CCSD(T)/cc-pVTZ//CCSD/cc-pVTZ optimized geometries of the critical points of Scheme 5 are drawn in Figure 2.

Scheme 5.

5
TS 5 → 3	3
TS 5 → 6	6
TS 5 → 4	4

Figure 2. CCSD/cc-pVTZ optimized geometries.¹

Any non-statistical effect would occur in the transition from 5 to 3. A direct dynamics trajectory analysis was performed starting in the neighborhood of this TS using three different functionals to generate the potential energy surface. Though only 100 trajectories were computed, the results with all three functionals are similar. About 2/3rds of these trajectories led to 3 followed by the shift of the C₅ methyl group. Another 15% led to 3 and then the C₁ methyl shifted. This MD simulation supports the non-statistical Wolff rearrangement, with a clear preference for the C₅ shift, consistent with experiment. A larger MD study is underway and will hopefully shed additional insight onto this fascinating reaction.

References

(1) Litovitz, A. E.; Keresztes, I.; Carpenter, B. K., "Evidence for Nonstatistical Dynamics in the Wolff Rearrangement of a Carbene," J. Am. Chem. Soc., 2008, 130, 12085-12094, DOI: 10.1021/ja803230a.

InChIs

3: InChI=1/C5H6O2/c1-4(6)3-5(2)7/h1-2H3
InChIKey = IGYQBMPIQGLNRU-UHFFFAOYAO

4: InChI=1/C5H6O2/c1-4(3-6)5(2)7/h1-2H3
InChIKey = ABVJXABNYINQLN-UHFFFAOYAA

5: InChI=1/C5H6O2/c1-3-5(7)4(2)6/h1-2H3
InChIKey = FJJXVDYICOYKRN-UHFFFAOYAD

6: InChI=1/C5H6O2/c1-4-3(6)5(4,2)7-4/h1-2H3
InChIKey = CAMBQRQJZBTNNS-UHFFFAOYAB

Consider bicorannulenyl 1. Each corranulene unit is a bowl and each is chiral due to being monosubstituted. Additional chirality is due to the arrangement of the bowls along the C₁-C_1’ bond, the bond where the two rings join. So both rotation about the C₁-C_1’ bond and bowl inversion will change the local chirality (Scheme 1 distinguishes these two processes.) One might anticipate that the stereodynamics of 1 will be complicated!

Scheme 1

Rabinovitz, Scott, Shenhar and their groups have tackled the stereodynamics of 1.¹ (This is a very nice joint experimental and theoretical study and I wonder why it did not appear in JACS.) At room temperature and above, one observes a single set of signals, a singlet and eight doublets, in the ¹H NMR. Below 200 K, there are three sets of signals, evidently from three different diastereomers.

Each ring can have either P or M symmetry. The authors designate conformations using these symbols for each ring along with the value of the torsion angle about the C₁-C_1’ bond. So, for example, a PP isomer is the enantiomer of the MM conformer when their dihedral angles are of opposite sign.

DFT computations help make sense of these results. PBE0/6-31G* computations reveal all local minima and rotational and inversion transition states of 1. The lowest (free) energy structure is PP₄₄ (see Figure 1). A very small barrier separates it from PP₁₁₁; this barrier is related to loss of conjugation between the two rings. Further rotation must cross a much larger barrier (nearly 17 and 20 kcal mol^-1). These barriers result from the interaction of the C₂ hydrogen of one ring with either the C_2’ or C_10’ hydrogen, similar to the rotational barrier in 1,1’-binaphthyl. However, the barrier is lower in 1 than in 1,1’-binaphthyl due to the non-planar nature of 1 that allows the protons to be farther apart in the TS. Once over these large barriers, two local minima, PP_-45 and PP_-137, separated by a small barrier are again found.

PP44 0.0	PP-28 19.80	PP-45 3.38
PP111 1.54	PP166 16.76	PP-137 0.14

Figure 1. PBE0/6-31G* optimized geometries and relative free energies (kcal mol^-1) of the PP local minima (PP₄₄, PP₁₁₁, PP_-45, and PP_-137) and rotational transition states.¹

The lowest energy bowl inversion transition state (P₄₉) lies 9.6 kcal mole^-1 above PP₄₄. It is shown in Figure 2. The bowl inversion barrier is comparable to that found in other substituted corannulenes,² which are typically about 9-12 kcal mol^-1).

P49 9.58

Figure 2. PBE0/6-31G* optimized geometry and relative free energy of the lowest energy bowl inversion transition state.¹

Interestingly, it is easier to invert the bowl than to rotate about the C₁-C_1’ bond. And this offers an explanation for the experimental ¹H NMR behavior. At low temperature, crossing the low rotational barriers associated with loss of conjugation occurs. So, using the examples from Figure 1, PP₄₄ and PP₁₁₁ appear as a single time-averaged signal in the NMR. This leads to three pairs of enantiomers (S.PP/R.PP, S.MM/R.PP, and S.PM/R.MP), giving rise to the three sets of NMR signals.

References

(1) Eisenberg, D.; Filatov, A. S.; Jackson, E. A.; Rabinovitz, M.; Petrukhina, M. A.; Scott, L. T.; Shenhar, R., "Bicorannulenyl: Stereochemistry of a C40H18 Biaryl Composed of Two Chiral Bowls," J. Am. Chem. Soc. 2008, 73, 6073-6078, DOI: 10.1021/jo800359z.

(2) Wu, Y. T.; Siegel, J. S., "Aromatic Molecular-Bowl Hydrocarbons: Synthetic Derivatives, Their Structures, and Physical Properties," Chem. Rev. 2006, 106, 4843-4867, DOI: 10.1021/cr050554q.

InChIs

1: InChIKey = XZISQKATUXKXQW-UHFFFAOYAG

Ken Houk has produced a very nice minireview on bifurcations in organic reactions.¹ This article is a great introduction to a topic that has broad implication for mechanistic concepts. Bifurcations result when a valley-ridge inflection point occurs on or near the intrinsic reaction coordinate. This inflection point allows trajectories to split into neighboring basins (to proceed to different products) without crossing a second transition state. In the examples discussed, the reactant crosses a single transition state and then leads to two different products. This is the so-called “two-step no intermediate” process.

I discuss the implications of these kinds of potential energy surfaces, and other ones of a pathological nature, in the last chapter of my book. Very interesting reaction dynamics often are the result, leading to a mechanistic understanding far from the ordinary!

References

(1) Ess, D. H.; Wheeler, S. E.; Iafe, R. G.; Xu, L.; Çelebi-Ölçüm, N.; Houk, K. N., "Bifurcations on Potential Energy Surfaces of Organic Reactions," Angew. Chem. Int. Ed. 2008, DOI: 10.1002/anie.200800918