Can a remote substituent affect the singlet-triplet spin state of a carbene? Somewhat surprisingly, the answer is yes. Sheridan has synthesized and characterized the meta and para methoxy-substituted phenyltrifluoromethyl)carbenes 1 and 2.¹ The UV-Vis spectrum of 1 is consistent with a triplet as its EPR and reactivity with oxygen. However, the para isomer 2 gave no EPR signal and failed to react with oxygen or hydrogen, suggestive of a singlet.

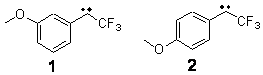
The conformations of 1 and 2 were optimized at B3LYP/6-31+G(d,p) and the lowest energy
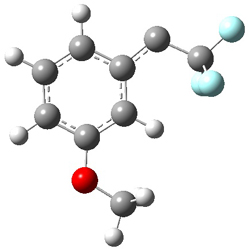
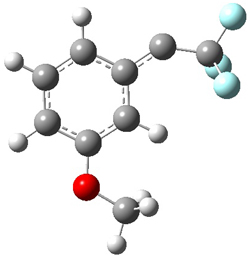
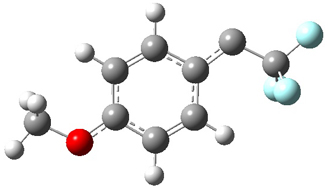
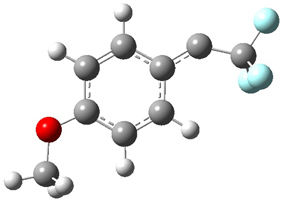
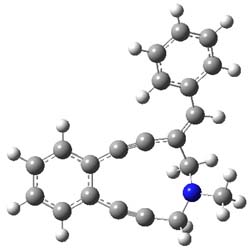
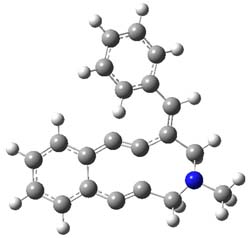
singlet and triplet conformers are shown in Figure 1. The experimental spectral features of 1 match up best with the computed features of the triplet, and the same is true for the singlet of 2.

1singlet	1triplet
2singlet	2triplet

Figure 1. B3LYP/6-31+G(d,p) optimized geometries of 1 and 2.

The triplet of 1 is estimated to be about 4 kcal mol^-1 below that of the singlet – larger than the general overestimation of the stability of triplets that beleaguer B3LYP. For 2, B3LYP predicts a singlet ground state.

The isodesmic reactions 1 and 2 help understand the strong substituent effect. For 1, the meta substituent destabilizes both the singlet and triplet by a small amount. For 2, the para methoxy group stabilizes the triplet slightly, but stabilizes the singlet by a large amount. This stabilization is likely the result of the contribution of a second resonance structure 2b. A large rotational barrier for both the methyl methyl and the trifluoromethyl groups supports the participation of 2b.

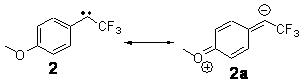
References

(1) Song, M.-G.; Sheridan, R. S., "Regiochemical Substituent Switching of Spin States in
Aryl(trifluoromethyl)carbenes," J. Am. Chem. Soc. 2011, 133, 19688-19690, DOI: 10.1021/ja209613u

InChIs

1: InChI=1/C9H7F3O/c1-13-8-4-2-3-7(5-8)6-9(10,11)12/h2-5H,1H3
InChIKey=CAHMVAJXXQQHDW-UHFFFAOYAA

2: InChI=1/C9H7F3O/c1-13-8-4-2-7(3-5-8)6-9(10,11)12/h2-5H,1H3
InChIKey

Synthetic application of the Bergman cyclization is rare. Basak reports a real interesting use of this reaction to create polycyclic aromatics.¹ So, for example, heating up 1 in DMSO leads to the 4helicene 2. The proposed mechanism is shown in Figure 1. The Bergman cyclization leads to the biradical 3, which adds to the pendant phenyl group to give 4. Hydrogen abstraction then gives 5, which abstracts hydrogens from the solvent to produce 6. (Use of DMSO-d ₆ provides deuterium incorporated products consistent with the diradical shown in 4.) Oxidation then gives the final product 2.

Figure 1. Proposed mechanism for the conversion of 1 to 2.

B3LYP computations were performed to examine the relative rates with substituents on the phenyl ring. The structure of 1’ (with a methyl group replacing the Ns group – 4-nitrobenzenesulfonyl) and the transition state for the Bergman cyclization are shown in Figure 2. Unfortunately, computations were not used to analyze the complete proposed mechanism – a project that awaits the eager student perhaps?

1’

1’TS

Figure 2. B3LYP/def2-TZVP//BP86/def2-TZVP optimized structures of 1’ and transition state for the Bergman cyclization of 1’.

References

(1) Roy, S.; Anoop, A.; Biradha, K.; Basak, A., "Synthesis of Angularly Fused Aromatic Compounds from Alkenyl Enediynes by a Tandem Radical Cyclization Process," Angew. Chem. Int. Ed., 2011, 50, 8316-8319, DOI: 10.1002/anie.201103318

InChIs

1’: InChI=1/C21H17N/c1-22-15-7-12-20-10-5-6-11-21(20)14-13-19(17-22)16-18-8-3-2-4-9-18/h2-6,8-11,16H,15,17H2,1H3/b19-16+
InChIKey=MKFCCTRNSOHUDU-KNTRCKAVBS

2’: InChI=1/C21H17N/c1-22-12-16-10-14-6-2-4-8-18(14)21-19-9-5-3-7-15(19)11-17(13-22)20(16)21/h2-11H,12-13H2,1H3
InChIKey=ZNCMIYYKBITIMW-UHFFFAOYAR

Bergman and Raymond have prepared a Ga₄L₆^12- host that can encapsulate small monocations and neutral species.^1,2 Figure 1 shows the host with an encapsulated tetraethylammonium ion NEt₄⁺. (Note that the hydrogens have been suppressed for easier viewing. And be sure to click on the structure in order to interact with the 3-D model.)

Figure 1. Structure of the Ga₄L₆^12- host encapsulating NEt₄⁺.

Of interest for readers of this blog is that they have now computed the NMR spectra of the encapsulated species.³ The geometry of the host is fixed to that found in the crystal structure where Cp*Co is the guest and the geometry of the guest (NEt₄⁺, PEt₄⁺ and others) is optimized with molecular mechanics. The complex is then computed at B3LYP with the 3-21G basis set for the host and the G-311(g,p) basis set for the guest. The computed ¹H chemical shifts are actually within 0.1 ppm of experiment, and show the swapping of the relative position of the chemical shifts of the methyl vs methylene proton for the two guests.

This demonstrates the computed NMR shifts can be applied to some very large molecules including organometallics.

References

(1) Caulder, D. L.; Powers, R. E.; Parac, T. N.; Raymond, K. N., "The Self-Assembly of a Predesigned Tetrahedral M₄L₆ Supramolecular Cluster," Angew. Chem. Int. Ed. 1998, 37, 1840-1843, DOI: 10.1002/(SICI)1521-3773(19980803)37:13/14<1840::AID-ANIE1840>3.0.CO;2-D

(2) Biros, S. M.; Bergman, R. G.; Raymond, K. N., "The Hydrophobic Effect Drives the Recognition of Hydrocarbons by an Anionic Metal-Ligand Cluster," J. Am. Chem. Soc. 2007, 129, 12094-12095, DOI: 10.1021/ja075236i

(3) Mugridge, J. S.; Bergman, R. G.; Raymond, K. N., "¹H NMR Chemical Shift Calculations as a Probe of Supramolecular Host-Guest Geometry," J. Am. Chem. Soc. 2011, 133, 11205-11212, DOI: http://dx.doi.org/10.1021/ja202254x

The [1,5]-H migration in cyclopentadiene seems like it should be a very ordinary reaction. A molecular dynamics study by Carpenter at first glance appears to confirm this notion.¹ Trajectories studies show that the ratio of endo:exo migration is very close to 1:1, suggesting, as expected, statistical behavior. However, inspection of the time dependence of the endo to exo migration shows oscillatory behavior. This oscillation corresponds to the B₁ vibration that effectively flips the methylene group through the ring plane and interchanges the exo and endo hydrogens. The hydrogen preferentially migrates from the endo position, with the ring bent by typically 10°, a point far from the computed [1,5]-H migration transition state (which is planar).

Differential damping this B₁ vibration should then lead to variable endo:exo ratios, and Carpenter suggests that performing this reaction in the gas phase and in solution with different solvent viscosities should exhibit such a variable ratio. The experiment awaits an experimenter!

Once again the take-home message is that dynamics matter, even in seemingly simple and well-understood processes. Reactions can take place far from the nominal transition state and the consequences can be significant.

References

(1) Goldman, L. M.; Glowacki, D. R.; Carpenter, B. K., "Nonstatistical Dynamics in Unlikely Places: [1,5] Hydrogen Migration in Chemically Activated Cyclopentadiene," J. Am. Chem. Soc. 2011, 133, 5312-5318, DOI: 10.1021/ja1095717

One of the great challenges to computational chemistry and computational biochemistry is rational design of enzymes. Baker and Houk have been pursuing this goal and in their recent paper they report progress towards an enzyme designed to catalyze a Diels-Alder reaction.¹

They envisaged an enzyme that could catalyze the Diels-Alder of 1 with 2 by having a suitable hydrogen bond acceptor of the carbamide proton of 1 (such as the carbonyl oxygen of glutamine or asparagine) along with a suitable donor to the oxygen of 2 (such as the hydroxyl of tyrosine, serine or threonine) – as shown below. Along with positioning the diene and dienophile near each other and properly orienting them for reaction, the activation barrier should be lowered by narrowing the HOMO-LUMO gap.

A series of transition states for the Diels-Alder reaction of 1 with 2 along with the hydrogen-bonded amino acids were optimized B3LYP/6-31+G(d,p) and used as constraints within the RosettaMatch code for locating a protein scaffold that could accommodate this TS structure. This resulted in 84 protein designs, each of which were synthesized and screened for activity in catalyzing the Diels-Alder reaction. Of these potential enzymes, 50 were soluble and of these 50, only 2 showed any activity. These two were selectively mutated to try to improve activity, and some improvement was obtained.

Of particular note is that mutation that removed one or both of the residues designed to hydrogen bond to the substrates resulted in complete loss of activity.

In principle 8 different steriosomeric products are possible in the reaction of 1 with 2. In solution in the absence of enzyme, four products are observed, with the major product (47%) the 3R,4S endo prodcut 3. The designed enzymes were constructed to make this product, and in fact it is the only observed stereoisomer formed in the reaction in the presence of enzyme. Furthermore, the designed enzymes are quite selective; for example, changing a single N-methyl group to N-ethyl on 2 reduced the rate by a factor of 2 and larger substituents resulted in a greater rate suppression.

Turnover rate is high and suggests that these enzymes might have real application in chemical synthesis. The disappointing aspect of the study was the poor ratio of predicted enzymes (84) to ones that actually had activity (2).

References

(1) Siegel, J. B.; Zanghellini, A.; Lovick, H. M.; Kiss, G.; Lambert, A. R.; St.Clair, J. L.; Gallaher, J. L.; Hilvert, D.; Gelb, M. H.; Stoddard, B. L.; Houk, K. N.; Michael, F. E.; Baker, D., "Computational Design of an Enzyme Catalyst for a Stereoselective Bimolecular Diels-Alder Reaction," Science, 2010, 329, 309-313, DOI: 10.1126/science.1190239

I missed this short communication last year, (thanks to the computational chemistry list CCL for bringing this to our attention!) but it is worth commenting on even a year later as this topic is one that frequently confuses users.

Ho, Klamt, and Coote¹ note that popular quantum chemistry codes, including the Gaussian series, present the output of continuum solvent models in a way that can be misleading. What is called the free energy is in fact the sum of the electronic energy in solution and the free energy associated with non-electrostatic contributions. What is missing are corrections to the solute to give its free energy. What is assumed (oftentimes without fully recognizing this assumption) is that the thermal corrections for the solute in the gas and solution phase will cancel – but this does not have to be. Let the QM code user (and reader of the literature) beware!

References

(1) Ho, J.; Klamt, A.; Coote, M. L., "Comment on the Correct Use of Continuum Solvent Models," J. Phys. Chem. A 2010, 114, 13442-13444, DOI: 10.1021/jp107136j

Suppose a compound could exist in one of two ways: (a) a symmetrical structure like the bromonium cation A or (b) equilibrating structures that on a time-average basis appear symmetrical, like B. How would one differentiate between these two possibilities?

Saunders developed a method whereby the species is isotopically labeled and then examined by NMR.^1-3 For case B, isotopic labeling will desymmetrize the two structures and so the chemical shifts of what were equivalent nuclei will become (often quite) different. But the isotopic labeling of A, while breaking the symmetry, does so to a much lesser extent, and the chemical shit difference of the (former) equivalent nuclei will be similar.

Singelton has employed this concept using both experiment and theory for two interesting cases.⁴ For the bromonium cation 1, Ohta⁵ discovered that the ¹³C NMR chemical shifts differed by 3.61 ppm with the deuterium labels. This led Ohta to conclude that the bomonium cation is really two equilibrating structures. It should be noted that the DFT optimized structure has C_2v symmetry (a single symmetric structure). Singleton applied a number of theoretical methods, the most interesting being an MD simulation of the cation. A large number of trajectories were computed and then the NMR shifts were computed at each point along each trajectory to provide a time-averaged difference in the chemical shifts of 4.8 ppm. Thus 2 can express a desymmetrization even though the unlabled structure is symmetric. This desymmetrization is due to coupling of vibrational modes involving the isotopes.

The second example is phthalate 2. Perrin observed a large ¹⁸O chemical shift difference upon isotopic labeling of one of the oxygen atoms, suggesting equilibrating structures.⁶ An MD study of such a system would take an estimated 1500 processor-years. Instead, by increasing the mass of the label to ²⁴O, the trajectories could be computed in a more reasonable time, and this would result in an isotope effect that is 4 times too large. The oxygen chemical shifts of more the 2.5 million trajectory points were computed for the two labeling cases, and each again showed a large chemical shift difference even though the underlying structure is symmetrical.

Thus, isotopic labeling can desymmetrize a symmetrical potential energy surface.

References

(1) Saunders, M.; Kates, M. R., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance spectra of deuterated cyclohexenyl and cyclopentenyl cations," J. Am. Chem. Soc., 1977, 99, 8071-8072, DOI: 10.1021/ja00466a061

(2) Saunders, M.; Telkowski, L.; Kates, M. R., "Isotopic perturbation of degeneracy. Carbon-13 nuclear magnetic resonance spectra of dimethylcyclopentyl and dimethylnorbornyl cations," J. Am. Chem. Soc., 1977, 99, 8070-8071, DOI: 10.1021/ja00466a060

(3) Saunders, M.; Kates, M. R.; Wiberg, K. B.; Pratt, W., "Isotopic perturbation of resonance. Carbon-13 nuclear magnetic resonance of 2-deuterio-2-bicyclo[2.1.1]hexyl cation," J. Am. Chem. Soc., 1977, 99, 8072-8073, DOI: 10.1021/ja00466a062

(4) Bogle, X. S.; Singleton, D. A., "Isotope-Induced Desymmetrization Can Mimic
Isotopic Perturbation of Equilibria. On the Symmetry of Bromonium Ions and Hydrogen Bonds," J. Am. Chem. Soc., 2011, 133, 17172-17175, DOI: 10.1021/ja2084288

(5) Ohta, B. K.; Hough, R. E.; Schubert, J. W., "Evidence for β-Chlorocarbenium and β-Bromocarbenium Ions," Organic Letters, 2007, 9, 2317-2320, DOI: 10.1021/ol070673n

(6) Perrin, C. L., "Symmetry of hydrogen bonds in solution," Pure Appl. Chem., 2009, 81, 571-583, DOI: 10.1351/PAC-CON-08-08-14.

How should one add diffuse functions to the basis set? Diffuse functions are known to be critical in describing the electron distribution of anions (as discussed in my book), but they are also quite important in describing weak interactions, like hydrogen bonds, and can be critical in evaluating activation barriers and other properties.

The Truhlar group has been active in benchmarking the need of basis functions and their recent review¹ summarizes their work. In particular, they recommend that for DFT computations a minimally augmented basis set is appropriate for examining barrier heights and weakly bound systems. A minimally augmented basis set would have s and p diffuse functions on heavy atoms for the Pople split-valence basis sets and the Dunning cc-pVxZ basis sets.

For wavefunction based computations, they recommend the use of the “jun-“ basis sets. The “jun” basis set is one of the so-called calendar basis set derived from the aug-cc-pVxZ, which includes diffuse functions of all types. So, for C in the aug-cc-pVTZ basis set, there are diffuse s, p, d, and f functions. The “jun-“ basis set omits the diffuse f functions along with all diffuse functions on H.

The great advantage of these trimmed basis sets is that they are smaller than the fully augmented sets, leading to faster computations. And since trimming off some diffuse functions leads to little loss in accuracy, one should seriously consider using these types of basis sets. As Truhlar notes, these trimmed basis sets might allow one to use a partially augmented but larger zeta basis set at the same cost of the smaller zeta basis that is fully augmented.

References

(1) Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H. R.; Truhlar, D. G., "Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions," J. Chem. Theory Comput., 2011,
7, 3027-3034, DOI: 10.1021/ct200106a

Bally and Rablen have followed up their important study of the appropriate basis sets and density functional needed to compute NMR chemical shifts¹ (see this post) with this great examination of procedures for computing proton-proton coupling constants.²

They performed a comparison of 165 experimental coupling constants from 66 small, rigid molecules with computed proton-proton coupling constants. They use a variety of basis sets and functionals. They also test whether all four components that lead to nuclear-nuclear spin coupling constants are need, or if just the Fermi contact term would suffice.

The computationally most efficient procedure, one that still provides excellent agreement with the experimental coupling constants is the following:

1. optimize the geometry at B3LYP/6-31G(d)
2. Calculate only the proton-proton Fermi contact terms at B3LYP/6-31G(d,p)u+1s[H]. The basis set used for computing the Fermi contact terms is unusual. The basis set for hydrogen (denoted as “u+1s[H]”) uncontracts the core functions and adds one more very compact 1s function.
3. Scale the Fermi contact terms by 0.9155 to obtain the proton-proton coupling constants.

This methodology provides coupling constants with a mean error of 0.51 Hz, and when applied to a probe set of 61 coupling constants in 37 different molecules (including a few that require a number of conformers and thus a Boltzmann-weighted averaging of the coupling constants) the mean error is only 0.56 Hz.

Bally and Rablen supply a set of scripts to automate the computation of the coupling constants according to this prescription; these scripts are available in the supporting materials and also on the Cheshire web site. It should also be noted that the procedure described above can be performed with Gaussian-09; no other software is needed. Thus, these computations are amenable to synthetic chemists with a basic understanding of quantum chemistry.

References

(1) Jain, R.; Bally, T.; Rablen, P. R., "Calculating Accurate Proton Chemical Shifts of Organic Molecules with Density Functional Methods and Modest Basis Sets," J. Org. Chem., 2009, 74, 4017-4023, DOI: 10.1021/jo900482q.

(2) Bally, T.; Rablen, P. R., "Quantum-Chemical Simulation of ¹H NMR Spectra. 2. Comparison of DFT-Based Procedures for Computing Proton-Proton Coupling Constants in Organic Molecules," J. Org. Chem., 2011, 76, 4818-4830, DOI: 10.1021/jo200513q

For those of you interested in learning about dispersion corrections for density functional theory, I recommend Grimme’s latest review article.¹ He discusses four different approaches to dealing with dispersion: (a) vdW-DF methods whereby a non-local dispersion term is included explicitly in the functional, (b) parameterized functional which account for some dispersion (like the M06-2x functional), (c) semiclassical corrections, labeled typically as DFT-D, which add an atom-pair term that typically has an r^-6 form, and (d) one-electron corrections.

The heart of the review is the comparison of the effect of including dispersion on thermochemistry. Grimme nicely points out that reaction energies and activation barriers typically are predicted with errors of 6-8 kcal mol^-1 with conventional DFT, and these errors are reduced by up to 1.5 kcal mol^-1 with the inclusion fo the “-D3” correction. Even double hybrid methods, whose mean errors are much smaller (about 3 kcal mol^-1), can be improved by over 0.5 kcal mol^-1 with the inclusion of the “-D3” correction. The same is also true for conformational energies.

Since the added expense of including the “-D3” correction is small, there is really no good reason for not including it routinely in all types of computations.

(As an aside, the article cited here is available for free through the end of this year. This new journal WIREs Computational Molecular Science has many review articles that will be of interest to readers of this blog.)

References

(1) Grimme, S., "Density functional theory with London dispersion corrections," WIREs Comput. Mol. Sci., 2011, 1, 211-228, DOI: 10.1002/wcms.30