The norbornyl cation has been a source of controversy for decades. Just what is the nature of this cation? Should one consider it a classical cation A or of some non-classical character B? A recent computational study adds further fuel to this fire.¹

The B3LYP/6-311G(d,p) structure of the norbornyl cation is shown in Figure 1, and this structure is little changed when reoptimized at PBE1PBE/6-311G(d,p) or CCSD/6-311G(d,p). Application of the topological method (sometimes referred to as atoms-in-molecules or AIM) reveals a bond path network that resembles the bicyclo[3.2.0]heptyl cation C. The C₁-C₂ distance is 1.75 Å and a bond path does connect these two atoms, though the density at the bond critical point is only 60% the value at the other C-C bonds in the compound. There is no bond path connecting C₁ to C₃ that would close up a three-member ring. The C₁-C₃ distance is 1.955 Å. So, the non-classical structure is not a proper description of this unusual species.

Figure 1. B3LYP/6-311G(d,p) optimized structure of the norbornyl cation.

References

(1) Werstiuk, N. H., "7-Norbornyl Cation – Fact or Fiction? A QTAIM-DI-VISAB Computational Study," J. Chem. Theory Comput., 2007, 3, 2258-2267, DOI: 10.1021/ct700176d.

In the book I extensively discuss the singlet-triplet gap of methylene and some of the chemistry of phenylcarbene. Schleyer and Schaefer have now reported computations on the singlet-triplet gap of arylcarbenes.¹ The geometries of phenylcarbene 1, diphenylcarbene 2, 1-naphthylcarbene 3, bis(1-naphtyl)carbene 4, and 9-anthrylcarbene 5 were optimized at B3LYP/6-311+G(d,p). These geometries are shown in Figure 1.

1s	1t
2s	2t
3s	3t
4s	4s
4s	4s

Figure 1. B3LYP/6-311+G(d,p) optimized structures of singlet and triplet 1-5.

Since this functional is known to underestimate the singlet-triplet gap of carbenes, they employ an empirical correction based on the difference in this gap for methylene between the computed value (11.89 kcal mol^-1) and the experimental value (9.05 kcal mol^-1). These corrected energy gaps are listed in Table 1.

Table 1. Corrected singlet-triplet energy gaps (kcal mol^-1) at B3LYP/6-311+G(d,p).

Using the following isodesmic reactions, they estimate the stabilization of the singlet or triplet carbene afforded by the aryl substituent:

R-C-H + CH₄ → H-C-H + R-CH₃

R-C-R + CH₄ → R-C-H + R-CH₃

These isodesmic energies are listed in Table 2. For phenylcarbne, the phenyl group stabilizes the singlet more than the triple, reducing the ST gap by 6.3 kcal mol^-1. However, adding a second phenyl group (making 2) stabilizes both the singlet and triplet by about the same amount, leading to little change in the ST gap. The singlet does not get accrue the potential benefit of the second aryl group because sterics prohibit the two rings from being coplanar.

Table 2. Aryl effect for 1-5 based on the isodesmic reaction energies (kcal mol^-1)

References

(1) Woodcock, H. L.; Moran, D.; Brooks, B. R.; Schleyer, P. v. R.; Schaefer, H. F., "Carbene Stabilization by Aryl Substituents. Is Bigger Better?," J. Am. Chem. Soc., 2007, 129, 3763-3770, DOI: 10.1021/ja068899t.

InChIs

1: InChI=1/C7H6/c1-7-5-3-2-4-6-7/h1-6H

2: InChI=1/C13H10/c1-3-7-12(8-4-1)11-13-9-5-2-6-10-13/h1-10H

3: InChI=1/C11H8/c1-9-5-4-7-10-6-2-3-8-11(9)10/h1-8H

4: InChI=1/C21H14/c1-2-8-19-14-16(12-13-17(19)6-1)15-20-10-5-9-18-7-3-4-11-21(18)20/h1-14H

5: InChI=1/C15H10/c1-11-14-8-4-2-6-12(14)10-13-7-3-5-9-15(11)13/h1-10H

Poutsma has followed up on the work he reported earlier in collaboration with Kass concerning the gas-phase acidity of the amino acids.¹ Their previous work reported on cysteine,² with the unusual result that the thiol group is more acidic than the carboxylic acid group. (I blogged on this a previous post.) Now, he reports the experimental and DFT acidities of all 20 amino acids, shown in Table 1. The experiments were done using the kinetic method in a quadrupole ion trap with electrospray ionization. The computations were performed at B3LYP/6-311++G**//B3LYP/6-31+G*, following some MM searching to identify low-lying conformations. The computed acidities were obtained relative to acetic acid, i.e. R-CH₂COOH + OAc^– → R-CH₂COO^– +HOAc.

Table 1. Relative acidities (kJ mol^-1) of the amino acids¹

The computed values are in very good agreement with the experimental values. The amino acids are ordered in increasing acidity in Table 1. The order predicted by experiment and DFT are quite close, and the disagreements are well within the error bar of the experiment.

Similar to the result for cysteine, tyrosine also displays unusual acidity. The alcohol proton is more acidic than the carboxylic acid proton. The structures of tyrosine, and its two conjugate
bases, one from loss of the phenolic proton and the other from loss of the carboxylic acid proton are shown in Figure 1. The stability of the tyrosine conjugate base from loss of the phenolic
hydrogen arises from both the stability of phenoxide and the internal hydrogen bond from the carboxylic acid proton to the amine. This is different that in the cysteine case, the thiolate anion is stabilized by an internal hydrogen bond from the carboylic acid group (see Figure 2c here).

tyrosine
Tyrosine conjugate base (loss of phenolic hydrogen)	Tyrosine conjugate base (loss of carboxylate hydrogen)

Figure 1. B3LYP/6-31G* optimized structures of tyrosine and its conjugate bases.¹

References

(1) Jones, C. M.; Bernier, M.; Carson, E.; Colyer, K. E.; Metz, R.; Pawlow, A.; Wischow, E. D.; Webb, I.; Andriole, E. J.; Poutsma, J. C., "Gas-Phase Acidities of the 20 Protein Amino Acids," Int. J. Mass Spectrom. 2007, 267, 54-62, DOI: 10.1016/j.ijms.2007.02.018.

(2) Tian, Z.; Pawlow, A.; Poutsma, J. C.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidity, H/D Exchange Experiments, and Computations on Cysteine and Its Conjugate Base," J. Am. Chem. Soc. 2007, 129, 5403-5407, DOI: 10.1021/ja0666194.

InChI

Tyrosine: InChI=1/C9H11NO3/c10-8(9(12)13)5-6-1-3-7(11)4-2-6/h1-4,8,11H,5,10H2,(H,12,13)/t8-/m0/s1

In their continuing efforts to build novel aromatic systems, Siegel and Baldridge report the preparation of the decapropyl analogue of the per-ethynylated corrannulene 1.¹ They were hoping that this might cyclize to the bowl 2. It is however stable up to 100 °C, however, the analogue 3 was obtained in the initial preparation of decapropyl-1.

The B3LYP/cc-pVDZ optimized structures of 1 and 3 are shown in Figure 1. 1 is bowl-shaped, reflecting the property of corranulene, but interestingly 3 is planar. The geometry of the {10]annulene is interesting as it is more consistent with the alkynyl resonance form B.

1

3

Figure 1. B3LYP/cc-pVDZ optimized structures of 1 and 3.¹

Siegel and Baldridge speculate that the conversion of 1 → 3 occurs by first undergoing the Bergman cyclization to give 4, which then opens to give 3. Unfortunately, they did not compute the activation barrier for this process. They do suggest that further cyclization to give the hoped for 2 might be precluded by the long distances between radical center and neighboring alkynes in 4, but the radicals are too protected to allowing trapping by the solvent, allowing for the formation of 3.

References

(1) Hayama, T.; Wu, Y. T.; Linden, A.; Baldridge, K. K.; Siegel, J. S., "Synthesis, Structure, and Isomerization of Decapentynylcorannulene: Enediyne Cyclization/Interconversion of C₄₀R₁₀ Isomers," J. Am. Chem. Soc., 2007, 129, 12612-12613 DOI: 10.1021/ja074403b.

InChIs

1: InChI=1/C40H10/c1-11-21-22(12-2)32-25(15-5)26(16-6)34-29(19-9)30(20-10)35-28(18-8)27(17-7)33-24(14-4)23(13-3)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

2: InChI=1/C40H10/c1-2-12-14-5-6-16-18-9-10-20-19-8-7-17-15-4-3-13-11(1)21-22(12)32-24(14)26(16)34-29(18)30(20)35-28(19)27(17)33-25(15)23(13)31(21)36-37(32)39(34)40(35)38(33)36/h1-10H

3: InChI=1/C40H12/c1-9-23-25(11-3)33-27(13-5)29(15-7)35-30(16-8)28(14-6)34-26(12-4)24(10-2)32-22-20-18-17-19-21-31(23)36-37(32)39(34)40(35)38(33)36/h1-8,17-18,31-32H/b18-17-

In section 4.4 of the book, I discuss in great detail the computational (and some experimental) studies of the benzynes, the formal diradicals created by loss of two hydrogen atoms from benzene. Now comes a very nice experimental study on a molecule that takes the next step: 1,3,5-tridehydrobenzene 1, benzene that lacks three hydrogen atoms. Sander reports the preparation and characterization of trifluoro-1,3,5-tridehydrobenzene 2.¹ The characterization of this novel molecule is made through comparison with computed IR spectra.

2 is prepared by flash vapor pyrolysis of 1,3,5-triiodo-2,4,6-trifluorobenezene
and then trapping the products in a low temperature matrix. Sander identifies five IR peaks of a product he believes is 2. These IR frequencies are listed in Table 1.

Table 1. Experimental and computed^a IR frequencies (cm^-1) and relative intensities of 2.

^aUBLYP/cc-pVTZ. ^bTransition state.

In order to confirm that this IR spectra comes from 2, Sander computed the structure and IR frequencies of both 1 and 2. The ²A₁ structure of 1 had been studied previously², but what had gone unnoticed is that another structure is possible, the ²B₂ state. These two states differ in the separation between C₁ and C₃. When the distance is short, the SOMO is of a₁ symmetry and this orbital has bonding character between these two carbon centers, giving rise to the ²A₁ state (1a). As the distance gets longer between C₁ and C₃, a b₂ orbital, having antibonding character between C₁and C₃, becomes lower in energy than the a₁ orbital, so that the structure is ²B₂ (1b). The UBLYP/cc-pVTZ optimized structures are shown in Figure 1. 1a is 2-3 kcal mol^-1 lower in energy than 1b. Furthermore, 1b has one imaginary frequency and is not a local energy minimum. Sander also optimized the structures of 2a and 2b¸ finding little effect due to the fluorine substitution.

1a

1b

Figure 1. UBLYP/cc-pVTZ optimized structures of 1a (²A₁) and 1b (²B₁).

The computed IR frequencies are listed in Table 1. The computed frequencies (and their relative intensities) of 2a match up strikingly well with those of the experiment. Sander concludes that 2a has in fact been prepared and characterized.

References

(1) Venkataramani, S.; Winkler, M.; Sander, W., "Trifluoro-1,3,5-tridehydrobenzene," Angew. Chem. Int. Ed. 2007, 46, 4888-4893, DOI: 10.1002/anie.200700536

(2) Cristian, A. M. C.; Shao, Y.; Krylov, A. I., "Bonding Patterns in Benzene Triradicals from Structural, Spectroscopic, and Thermochemical Perspectives," J. Phys. Chem. A 2004, 108, 6581-6588, DOI: 10.1021/jp049007j.

InChI:

1: InChI=1/C6H3/c1-2-4-6-5-3-1/h1,4-5H
2: InChI=1/C6F3/c7-4-1-5(8)3-6(9)2-4

Kass has once again uncovered a simple system that challenges our notions of basic chemical concepts. It is a well accepted notion that the most acidic proton of all of the amino acids is the carboxylic acid one. However, acidities are strongly influenced by the solvent, and the absence of solvent in the gas phase can dramatically alter things.

Kass and co-workers examined the gas-phase acidity of cysteine with computational and
experimental techniques.¹ The lowest energy conformer of cysteine is 1a, characterized by having three intramolecular hydrogen bonds (Figure 1). The next lowest conformer, 1b, has only two intramolecular hydrogen bonds and is 1.5 kcal mol^-1 higher in energy at G3B3.

1a xyz	1b xyz

Figure 1. B3LYP/aug-cc-pVDZ optimized structures of cysteine 1.¹

They optimized a number of different configurations of the conjugate base of cysteine: two conformers from the loss of the carboxylate proton (2a and 2b), two conformers from the loss of the thiol proton (2c and 2d), and one conformer from the loss of the thiol proton of the zwitterion (2e). These structures are shown in Figure 2 along with their relative energies. All of these structures possess two intramolecular hydrogen bonds.

2a (3.1) xyz	2b (3.4) xyz
2c (0.0) xyz	2d (5.1) xyz
2e (10.1) xyz

Figure 2. B3LYP/aug-cc-pVDZ optimized structures of the conjugate base of cysteine 2. Relative energies (kcal mol^-1) in parenthesis computed at G3B3.¹

The gas phase acidity of carboxylic acids is greater than thiols; the deprotonation energy of propanoic acid (CH₃CH₂CO₂H) is 347.7 kcal mol^-1 at G3B3 (347.2 expt.²), about 6 kcal mol^-1 less than that of ethanethiol (CH₂CH₂SH: 355.0 at G3B3 and 354.2 expt.²). However, the computations indicate that 2c is the lowest energy structure of deprotonated cysteine, and 2c comes about by loss of the thiol proton! Te lowest energy cysteine conjugate base from loss of the carboxylate proton is 1a, which is 3.1 kcal mol^-1 higher in energy. Apparently, the hydrogen bonding network in 2c is quite favorable, able to make up for the inherent favorability of a carboxylate over a thiolate anion.

The G3B3 computed deprotonation energy of cysteine is 333.3 kcal mol^-1 (for removal of the thiol proton). Kass determined the deprotonation energy of cysteine using a kinetic and a thermodynamic method. The kinetic method gives a value of 332.9 ± 3.3 kcal mol^-1­, while the thermodynamic method gives 334.4 ± 3.3 kcal mol^-1­. These are in fine agreement with the computed value.

This study ably demonstrates the dramatic role that solvent can play in determining molecular properties. Kass titled the article “Are carboxyl groups the most acidic sites in amino acids?” and answers with “no” – in the gas phase the thiol group is more acidic. He ends the article with an indication that the alcohol of tyrosine may be competitive in acidity with its carboxylic group, too.

References

(1) Tian, Z.; Pawlow, A.; Poutsma, J. C.; Kass, S. R., "Are Carboxyl Groups the Most Acidic Sites in Amino Acids? Gas-Phase Acidity, H/D Exchange Experiments, and Computations on Cysteine and Its Conjugate Base," J. Am. Chem. Soc., 2007, 129, 5403-5407, DOI: 10.1021/ja0666194.

(2) NIST, NIST Chemistry WebBook, 2005, http://webbook.nist.gov/.

InChIs

1: InChI=1/C3H7NO2S/c4-2(1-7)3(5)6/h2,7H,1,4H2,(H,5,6)

Kinked polycyclic benzoids are more stable that their straight chain analogues. For example, the gaseous heat of formation of phenanthrene 1 is 49.6 kcal mol^-1 while that of anthracene 2 is 55.2 kcal mol^-1.¹ This stability of the kinked over the straight chain is reproduced by computation: 1 is 4.24 kcal mol^-1 lower in energy than 2 at BLYP/TZ2P.href="#phenanref2">² The standard explanation for this has been better resonance in 1 than in 2, leading to 1 being more aromatic than 2.

Bader has recently offered at alternative explanation. Topological electron density analysis³ (also referred to as Atoms-In-Molecules, or AIM) examines the electron density distribution to uncover chemically-relevant information. The bond path traces out the ridge of maximum electron density between two atoms, passing through the bond critical point. Bader has argued that the existence of the bond path is the necessary and sufficient condition for a chemical bond. In the AIM analysis of 1, he noted a bond path connecting the hydrogen atoms on C₄ and C₅.⁴ These are the hydrogen atoms in the bay region, labeled explicitly in the sketch above. Based on this bond path, and the fact that the bay region hydrogen atoms are stabilized due to charge transfer from carbon, Bader argued that H-H bonding in 1 stabilizes this molecule, accounting for its lower heat of formation than 2.

In a 2007 JOC paper, Bickelhaupt directly attacked this contention.² The BLYP/TZ2P geometries of 1 and 2 are shown in Figure 1.

1

2

Figure 1. BLYP/TZ2P optimized geometries of 1 and 2.²

He approached the problem by examining the reaction of two 2-methtriylphenyl moieties combining to form either 1 or 2 (Scheme 1). The binding energy ΔE is then decomposed into two terms, ΔE_prep which is the energy required to deform the triradical fragment 3 from its optimum geometry into the geometry within either 1 or 2, designated as 3(1) or 3(2), and ΔE_int which is the interaction energy of the deformed fragments.

Scheme 1.

The deformation energy of the triradical fragment is nearly identical for 1 and 2. Therefore, the interaction energy to from 1 is more negative (stabilizing) than to form 2. The interaction energy for 1 was also obtained in two other ways. First, 3 was fixed to its geometry in 2 (i.e., 3(2)) with the distance of the two forming C-C bonds also that of 2. The interaction energy defined this way is -0.69 kcal mol^-1, indicating a preference for aligning the fragments in the orientation of phenanthrene. Bickelhaupt further partitions the interaction energy to σ- and π-components, and finds the stabilization of the model interaction energy is dominated by π-interactions, not the σ-interactions one would expect from Bader’s model of H-H stabilization. Allowing the C-C distances between the two 3(2) fragments to adjust to those in 1 further strengthens the interaction energy to -2.49 kcal mol^-1. The geometrical changes allow for the p-bonds to strengthen (by shortening the C₉-C₁₀ distance), and the repulsion between the bay area hydrogen atoms to diminish (by lengthening the C_4a-C_4b distance).

Bickelhaupt argues that the presence of a bond path may simply be due to two atomic basins being forced to bump into each other, whether these contacts be stabilizing or destabilizing. For example, two benzene molecules arranged such that a C-H bond points toward the C-H bond of another (see 4), a bond path will connect the two hydrogen atoms and the AIM energies of these two hydrogen atoms will indicate a net stabilization. He concludes by calling into question the basis for the claim that a bond path is the necessary and sufficient conditions for a chemical bond.

InChI:

1: InChI=1/C14H10/c1-3-7-13-11(5-1)9-10-12-6-2-4-8-14(12)13/h1-10H

2: InChI=1/C14H10/c1-2-6-12-10-14-8-4-3-7-13(14)9-11(12)5-1/h1-10H

References

(1) Cox, J. D.; Pilcher, G. Thermochemistry of Organic and Organometallic Compounds; Academic Press: New York, 1970.

(2) Poater, J.; Visser, R.; Sola, M.; Bickelhaupt, F. M., "Polycyclic Benzenoids: Why Kinked is More Stable than Straight," J. Org.Chem. 2007, 72, 1134-1142, DOI: 10.1021/jo061637p

(3) Bader, R. F. W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990.

(4) Matta, C. F.; Hernández-Trujillo, J.; Tang, T.-H.; Bader, R. F. W., "Hydrogen-Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals," Chem. Eur. J. 2003, 9, 1940-1951, DOI: 10.1002/chem.200204626

In the pursuit of further elucidation of just what the concepts “aromatic” and “antiaromatic” mean, Schleyer and Bunz reported the preparation and characterization of a novel antiaromatic compound that is isolable.¹

Bunz synthesized the redox pair of compounds 1 and 2 that differ in the electron count in the pi-system. The former (1) has 14 π electrons and should be aromatic, while the latter (5) has 16 π electrons and should be antiaromatic. The NMR spectrum of both compounds was measured and compared to the computed signals of the parent compounds 3 and 4. The signals match very nicely. The structures of 1 and 2 were further confirmed by x-ray crystallography. 1 and 2 can be interconverted by redox reactions and 2 is stable in air, only slowly oxidizing to 1.

The NICS(0)_πizz values computed for 3 and 4 are shown in Figure 1. (See ref 2 for a discussion on this NICS method and also Chapter 2 of my book.) These values are quite negative for each ring of 3, consistent with its expected aromatic character. On the other hand, the NICS value for each ring of 4 is more positive than the corresponding ring of 3, with the value in the center of the pyrazine ring being positive. These NICS values indicate that 4 is certainly less aromatic than 3, and perhaps even expresses antiaromatic character.

Figure 1. NICS(0)_πzz values for 3 and 4 computed at PW91/6-311G**.

Interestingly, hydrogenation of 3 to give 4 is -14.0, indicating that while 3 appears to be a normal aromatic compound, 4, if it is antiaromatic, exhibits some energetic stabilization. They identify this stabilization as a result of the interaction between the dihydropyrazine ring and the thidiazole ring, evidenced in the exothermicity of the isodemic reaction:

So while 4 may be antiaromatic, it appears to be energetically reasonably stable. It is important to keep in mind though that 4 is not the most stable tricycle isomer; in fact, 5 is 7 kcal mol^-1 lower in energy than 4.

Schleyer and Bunz conclude that antiaromaticity may “not result in a prohibitive energetic penalty.”

References

(1) Miao, S.; Schleyer, P. v. R.; Wu, J. I.; Hardcastle, K. I.; Bunz, U. H. F., "A Thiadiazole-Fused N,N-Dihydroquinoxaline: Antiaromatic but Isolable," Org. Lett. 2007, 9, 1073-1076, DOI: 10.1021/ol070013i

(2) Fallah-Bagher-Shaidaei, H.; Wannere, C. S.; Corminboeuf, C.; Puchta, R.; Schleyer, P. v. R., "Which NICS Aromaticity Index for Planar π Rings Is Best?," Org. Lett., 2006, 8, 863-866, DOI: 10.1021/ol0529546.

InChI

3: InChI=1/C8H4N4S/c1-2-10-6-4-8-7(11-13-12-8)3-5(6)9-1/h1-4H
4: InChI=1/C8H6N4S/c1-2-10-6-4-8-7(11-13-12-8)3-5(6)9-1/h1-4,9-10H
5: InChI=1/C8H6N4S/c1-2-10-6-4-8-7(11-13-12-8)3-5(6)9-1/h1-2H,3-4H2

In Chapter 1.6.2 we discuss computed NMR spectra, and in particular note some successes in correlating predicted chemical shifts with experiment values. Recently, Rychnovsky took the next logical step, utilizing computational methods to predict the NMR spectrum of a compound whose structure was in doubt.

Hexacyclinol was isolated from Panus Rudis, a type of mushroom. Based on spectroscopic studies, Gräfe proposed 1 as its structure.¹ Le Clair claimed to have synthesized a substance with this structure in 2006.² This article became a cause célèbre in the blogosphere,³ with serious doubts cast upon the veracity of the author and his claims.

Rychnovsky⁴ doubted that the molecule actually possessed the unusual structure of 1. Since the actual structure was unknown, he proposed to compute the NMR shifts based on the optimized structure of 1 and compare them with the experimental values. Given the very large size of hexacyclinol, the computational approach would have to be rather limited. Therefore, whatever (small) method was to be employed would have to be tested for adequate predictive performance with known compounds. Rychnovsky selected the three diterpenes elisapterosin B 2, elisabethin A 3, and maoecrystal V 4 to benchmark his computations. His computational approach was to first utilize a Monte Carlo search with the MMFF force field to identify low lying conformers. The best conformer was then optimized at HF/3-21G and the chemical shifts were computed using this geometry with the GIAO/mPW1PW91/6-31G(d,p). The optimized structures of the diterpenes 2-3 are shown in Figure 1.

elisapterosin B 2 xyz file PubChem entry
elisabethin A 3 xyz file
maoecrystal V 4 xyz file

Figure 1. HF/3-21G optimized structures of 2-3.⁴

The computed ¹³C chemical shifts for these test compounds were then plotted against the experimental values and a linear fit was determined to correct the computed values. The average ¹³C chemical shift difference between computation and experiment is less than 2 ppm, and no difference exceeds 5 ppm. Next, Rychnovsky optimized the proposed structure of hexacyclinol 1, shown in Figure 2, and computed its ¹³C chemical shifts and corrected them using the fitting procedure developed for the three test compounds. These computed chemical shifts were in poor agreement with the experimental values; the average deviation was 6.8 ppm and five shifts differ by more than 10 ppm. Rychnovsky concluded that this poor agreement discredits the proposed structure 1.

1
xyz file

Figure 2. HF/3-21G optimized structures of 1.⁴

As an alternative, Rychnovsky proposed that hexacyclinol is in fact the by-product from work-up of the natural product panepophenanthrin, also obtained from Panus rudis. He proposed that hexacylinol has the structure shown in 5. He optimized the geometry of 5 and obtained two low-energy conformers. The second-lowest conformer, shown in Figure 3, has a predicted ¹³C NMR spectrum in very close agreement with experiment. Its average chemical shift deviation is 1.8 ppm with a maximum difference of 5.8 ppm. These differences are consistent with those found in the diterpenes test set. This structure has now been synthesized by Porco and its x-ray structure obtained.⁵ This compound has the structure predicted by Rychnovsky and is completely consistent with the original hexacyclinol compound reported by Gräfe. This successful resolution of the structure of hexacycliinol should spur further use of computational methods to predict NMR spectra and evaluate chemical structures. ACD has recently applied its method for predicting NMR spectra to the problem of hexacylinol.⁶ You can read about this on the ChemSpider blog.

5 xyz file

Figure 3. HF/3-21G optimized structures of 5.⁴

References

(1) Schlegel, B.; Hartl, A.; Dahse, H.-M.; Gollmick, F. A.; Gräfe, U.; Dorfelt, H.; Kappes, B., “Hexacyclinol, a New Antiproliferative Metabolite of Panus Rudis HKI 0254,” J. Antibiot. 2002, 55, 814-817.

(2) La Clair, J. J., “Total Syntheses of Hexacyclinol, 5-epi-Hexacyclinol, and Desoxohexacyclinol Unveil an Antimalarial Prodrug Motif,” Angew. Chem. Int. Ed. 2006, 45, 2769-2773, DOI: 10.1002/anie.200504033

(3) (a) Halford, B., “Hexacyclinol Debate Heats Up,” Chem. Eng. News 2006, 84 (31, July 28), 11, http://pubs.acs.org/cen/news/84/i31/8431notw1.html. (b) Love, D. “Hexacyclinol? Or Not?” http://pipeline.corantte.com/archives/2006/06/05/hexacyclinol_or_not.php (c) “Structure Revision of Hexacyclinol”, http://totallynthetic.com/blog/?p=110 (d) Halford, B., “Hexacyclinol Showdown: The Biggest Non-Event at the ACS Meeting”, http://cenonline.blogs.com/sanfrancisco_2006/2006/09/hexacyclinol_sh.html (e) “Hexacyclinol Rides Again”, http://www.healthvoices.com/feed/items/blog_perspective/consultants/pharma/2006/07/3/hexacyclinol_rides_again

(4) Rychnovsky, S. D., “Predicting NMR Spectra by Computational Methods: Structure Revision of Hexacyclinol,” Org. Lett. 2006, 8, 2895-2898, DOI: 10.1021/ol0611346

(5) Porco, J. A. J.; Shun Su, S.; Lei, X.; Bardhan, S.; Rychnovsky, S. D., “Total Synthesis and Structure Assignment of (+)-Hexacyclinol,” Angew. Chem. Int. Ed. 2006, 45, 5790-5792, DOI: 10.1002/anie.200602854
(6) Elyashberg, M. E.; Williams, A. J.; Martin, G. E., “Computer-Assisted Structure Verification and Elucidation Tools in NMR-Based Structure Elucidation,” Prog. Nuc. Mag. Res. Spectrosc., 2007, in press, DOI: 10.1016/j.pnmrs.2007.04.003.

InChI

1: InChI=1/C23H28O7/c1-8(2)6-11-23-10(22(3,4)27-5)7-9-12(21(23)26)13-15(23)18(30-29-11)14(17(13)25)19-20(28-19)16(9)24/h6-7,10-15,17-20,25H,1-5H3/t10-,11+,12?,13?,14?,15?,17-,18?,19+,20+,23?/m1/s1

2: InChI=1/C20H26O3/c1-9(2)14-13-8-11(4)12-7-6-10(3)15-16(21)17(22)19(14,5)18(23)20(12,13)15/h10-14,21H,1,6-8H2,2-5H3/t10-,11-,12+,13-,14-,19+,20-/m0/s1

3: InChI=1/C20H28O3/c1-10(2)8-14-9-12(4)15-7-6-11(3)16-18(22)17(21)13(5)19(23)20(14,15)16/h8,11-12,14-16,21H,6-7,9H2,1-5H3/t11-,12-,14?,15+,16-,20-/m1/s1

4: InChI=1/C19H22O5/c1-10-11-4-7-18(13(10)21)17-9-23-15(22)19(18,8-11)24-14(17)16(2,3)6-5-12(17)20/h5-6,10-11,14H,4,7-9H2,1-3H3/t10-,11-,14-,17?,18-,19+/m1/s1

5: InChI=1/C23H28O7/c1-8(2)6-11-23-10(22(3,4)27-5)7-9-12(15(25)18-17(29-18)14(9)24)13(23)16(28-11)19-20(30-19)21(23)26/h6-7,10-13,15-20,25H,1-5H3/t10-,11+,12?,13?,15+,16+,17-,18-,19-,20?,23-/m0/s1

Castro and Karney¹ previously predicted a Möbius aromatic transition state for the π-bond shift in [12]annulene (see Chapter 2.4.3.1), a process they termed “twist-couple bond shifting”. In late 2006 they turned their attention to the conformational surface of [16]annulene, searching again for Möbius aromatic ground or transition states.²

Oth synthesized [16]annulene by the photolysis of cycloctatetraene dimer. He observed two isomers 1a and 2a in a 83:17 ratio³ at -140 °C, with a barrier⁴ of 10.3 kcal mol^-1 separating them. The ¹H NMR spectrum at -30 °C shows only one signal. The equivalence of all of the protons implicates rapid conformational changes and bond shifting, as suggested in Scheme 1. Also noted was that these conversions, including the configuration change from 1 to 2, have barriers much lower than for the electrocyclization of Reaction 1 of about 22 kcal mol^-1.⁵

Scheme 1
	Reaction 1

Following on the results from their [12]annulene study, Castro and Karney optimized geometries at BH&HLYP/6-311+G(d,p). Since, as we discussed in Chapter 2.4.3.1, relative energies of annulene conformations are very sensitive to the computational method and basis set, they determined estimated CCSD(T)/cc-pVDZ energies, which I will call E_est, according to a prescription proposed by Bally and MacMahon,⁶ namely

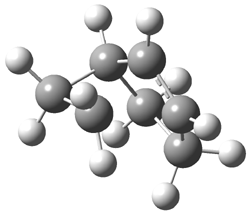
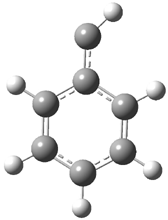
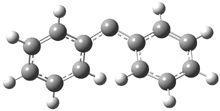
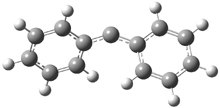
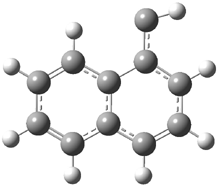
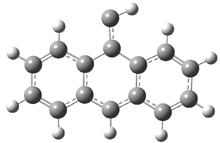
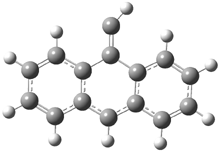
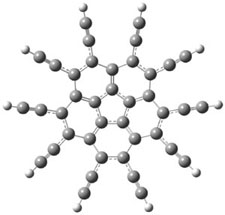
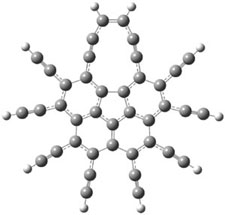
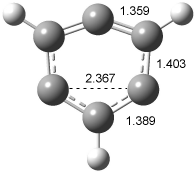
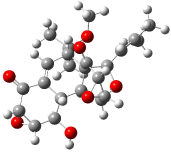
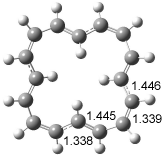
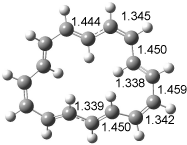
The optimized structures of 1a and 2a are drawn in Figure 1. Both molecules are not planar, their bond lengths are clearly alternating, and their NICS(0) values are +6.4 ppm (1a) and +7.3 ppm (2a), all evidence that neither molecule is aromatic. 1a is predicted to be 0.8 kcal mol^-1 lower in energy than 2a, consistent with experiment.

1a (0.0) xyz file	1b (5.6) xyz file
1c (5.4) xyz file	1d (7.7) xyz file
2a (0.8) xyz file	2b (4.1) xyz file
TS-1c2b (13.7) xyz file

Figure 1. BH&HLYP/6-311+G(d,p) optimized geometries and relative energies (kcal mol^-1) based on E_est.²

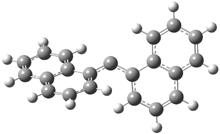
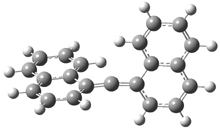
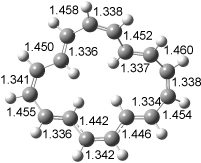
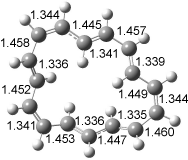
The conformational change 1a → 1a’ is a multi-step process. This is in contrast to [12]annulene where this change occurs via a concerted mechanism. So, 1a first converts to 1c through a barrier of 7.9 kcal mol^-1. The path now splits; 1b can next be formed with a barrier of 9.4 kcal mol^-1 to give 1c’ or 1d can be formed through a barrier of 7.7 kcal mol^-1 to produce 1c’. 1c’ converts to 1a’ with a barrier of 7.9 kcal mol^-1. The structures of the intermediates and their relative energies are shown in Figure 1.

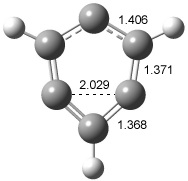
The conversion of 1 to 2 takes place through the transition state TS-1c2b that actually connects isomer 1c to 2b. This structure, shown in Figure 1, exhibits little bond alternation and has a NICS(0) value of -14.2, both strongly suggestive of Möbius aromatic character. Aromaticity should also imply energetic stabilization; TS-1c2b lies only 13.7 kcal mol^-1 above 1a. This barrier is less than that predicted for the twist-coupled bond shift in either [10]annulene or [12]annulene.

The highest barrier for the various interconversions indicated in Scheme 1 is the barrier associated with TS-1c2b. This barrier (13.7 kcal mol^-1) is significantly lower that the activation energy for Reaction 1 (22 kcal mol^-1). These computations confirm that the scrambling of the protons of [16]annulene is due to the rapid rearrangements of Scheme 1. Furthermore, the computations demonstrate that the key step is a twist-coupled bond shift that is facilitated by the Möbius aromatic character of its transition state.

Since the configuration change in [12]- and [16]annulene proceeds with a bond-shifting Möbius aromatic bond shifting transition state, might not the configuration change of [14]annulene proceed through a Möbius antiaromatic bond shifting transition state? In 2007, Castro and Karney⁷ answered this question in the affirmative.

Consistent with their previous studies, geometries were optimized at UBH&HLYP/6-311+G**. The unrestricted method is necessary since the expected antiaromatic transition state will have singlet radical character. In order to obtain reasonable energies, CASPT2(14,14)/cc-pVDZ single-point computations were employed.

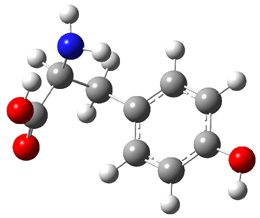
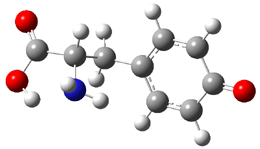
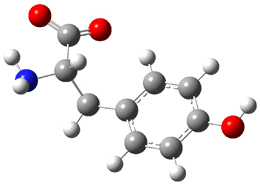
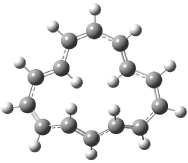
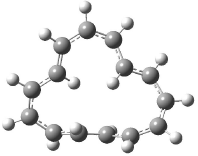
[14]annulene must undergo two conformational changes (3a-c) before the bond shift/configuration change can occur through transition state 4 to give 5. Note that this process changes the number of cis and trans double bonds. This overall process is shown in Figure 2. The optimized structures of 3c, 4, and 5 are shown in Figure 3.

Figure 2. CASPT2(14,14)/cc-pVDZ// UBH&HLYP/6-311+G** relative energies of stable structures along the pathway for configuration change of [14]annulene.

The computed barrier for the configuration change (through 4) is computed to be 19.3 kcal mol-1, in very reasonable agreement with the experimental value⁴ of 21.3 kcal mol-1.

3c

4

5

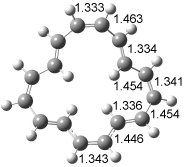
Figure 3. UBH&HLYP/6-311+G** optimized geometries of 3c, 4, and 5.⁷

Based on its magnetic properties, transition state 4 has decided antiaromatic character. Its computed NICS(0) value is +19.0 ppm. Compare this to the NICS(0) values for 3a and 5 of -8.0 and -5.0 ppm, respectively. In addition, the computed chemical shifts of the two interior protons are very downfield, 26.4 and 26.7 ppm.

InChI

1: InChI=1/C16H16/c1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1/h1-16H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7-,10-8-,11-9-,12-10+,13-11+,14-12+,15-13+,16-14-,16-15-

2: InChI=1/C16H16/c1-2-4-6-8-10-12-14-16-15-13-11-9-7-5-3-1/h1-16H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7+,10-8+,11-9+,12-10+,13-11-,14-12-,15-13-,16-14+,16-15+

3: InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2+,5-3+,6-4+,7-5+,8-6-,9-7-,10-8+,11-9+,12-10+,13-11+,14-12-,14-13-

5: InChI=1/C14H14/c1-2-4-6-8-10-12-14-13-11-9-7-5-3-1/h1-14H/b2-1-,3-1-,4-2-,5-3+,6-4+,7-5+,8-6+,9-7-,10-8-,11-9-,12-10-,13-11-,14-12+,14-13+

References

(1) Castro, C.; Karney, W. L.; Valencia, M. A.; Vu, C. M. H.; Pemberton, R. P., “Möbius Aromaticity in [12]Annulene: Cis-Trans Isomerization via Twist-Coupled Bond Shifting,” J. Am. Chem. Soc. 2005, 127, 9704-9705, DOI: 10.1021/ja052447j.

(2) Pemberton, R. P.; McShane, C. M.; Castro, C.; Karney, W. L., “Dynamic Processes in [16]Annulene: Change,” J. Am. Chem. Soc. 2006, 128, 16692-16700, DOI: 10.1021/ja066152x

(3) Oth, J. F. M.; Anthoine, G.; Gilles, J.-M., “Le dianion du [16] annulene,” Tetrahedron Lett. 1968, 9, 6265-6270, DOI: 10.1016/S0040-4039(00)75449-9.

(4) Oth, J. F. M., “Conformational Mobility and Fast Bond Shift in the Annulenes,” Pure Appl. Chem. 1971, 25, 573-622.

(5) Schroeder, G.; Martin, W.; Oth, J. F. M., “Thermal and Photochemical Behavior of a [16]Annulene,” Angew. Chem. Int. Ed. Engl. 1967, 6, 870-871, DOI: 10.1002/anie.196708701.

(6) Matzinger, S.; Bally, T.; Patterson, E. V.; McMahon, R. J., “The C₇H₆ Potential Energy Surface Revisited: Relative Energies and IR Assignment,” J. Am. Chem. Soc. 1996, 118, 1535-1542, DOI: 10.1021/ja953579n.

(7) Moll, J. F.; Pemberton, R. P.; Gutierrez, M. G.; Castro, C.; Karney, W. L., “Configuration Change in [14]Annulene Requires Möbius Antiaromatic Bond Shifting,” J. Am. Chem. Soc. 2007, 129, 274-275, DOI: 10.1021/ja0678469.