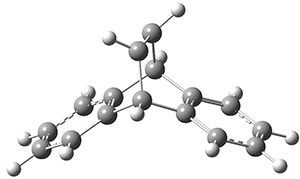
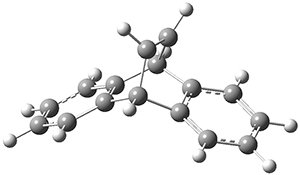
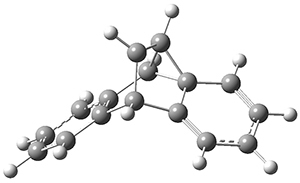
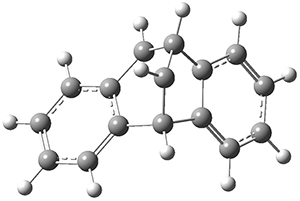
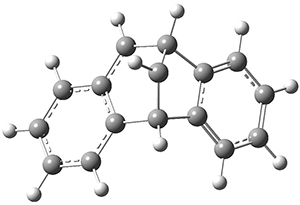
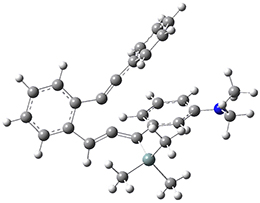
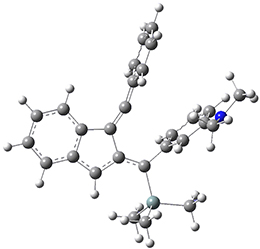
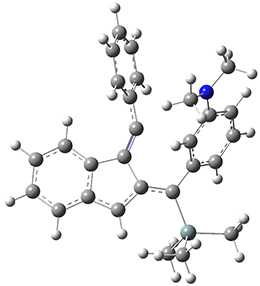
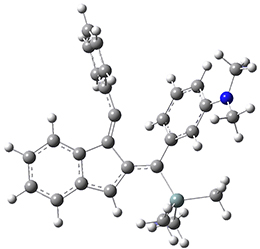
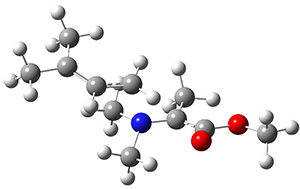
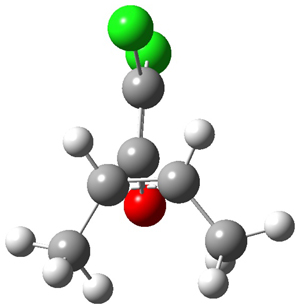
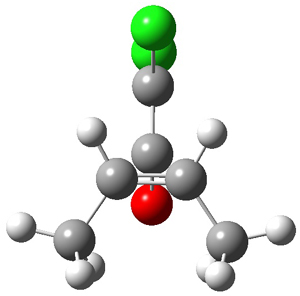
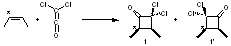The di-π-methane photorearrangement has been known for many years, first studied by Zimmerman.^1,2 The triplet photorearrangement gives an interesting rearranged product; and the mechanism of this photorearrangement of 1 into 2 has now been examined by the Houk group using computational techniques, including trajectory analysis. The proposed mechanism is that excitation to the triplet state 1* is followed by rearrangement to the triplet intermediate INT1* which then rearranges to the triplet INT2*. Intersystem crossing then leads to the singlet product 2.

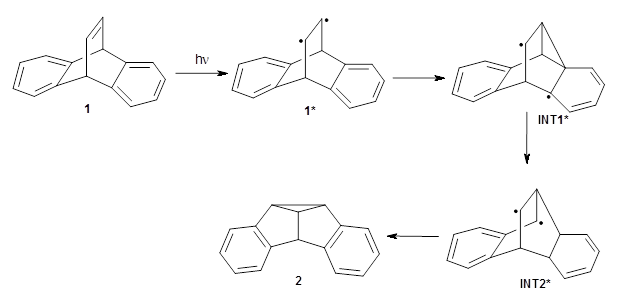
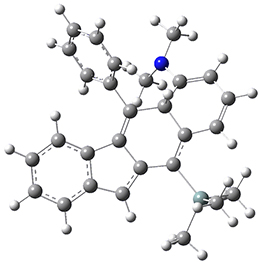
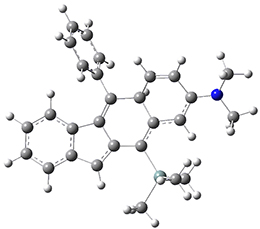
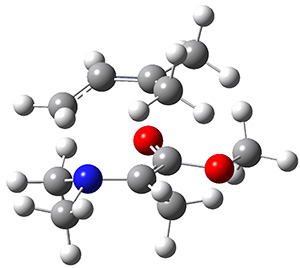
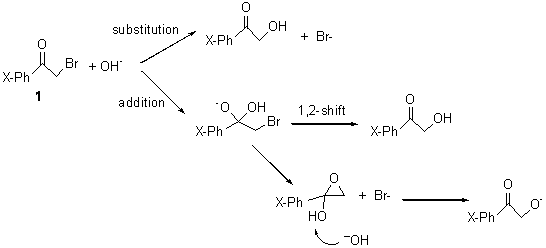
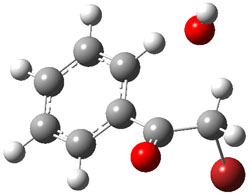
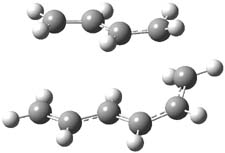
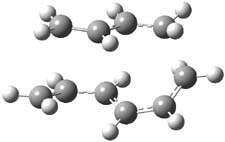
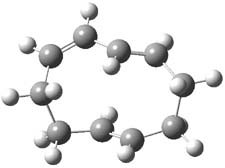
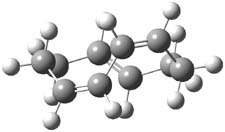
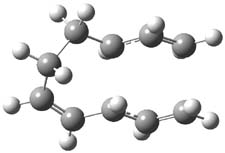
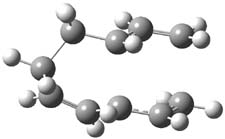
The PES for this rearrangement was explored³ at CASMP2(10,10)/6-31G(d)//CASSCF(10,10)/6-31G(d), with geometries and relative energies shown in Figure 1, as well as at (U)M06-2x/6-31G(d) and (U)B3LYP/6-31G(d); they all give qualitatively the same result. The first TS is the rate limiting step, and the second TS lies only 1-2 kcal mol^-1 above the intermediate INT1. So, the reaction appears to be two steps, but with such a low barrier for the second step, dynamic effects might be important as trajectories might cross INT1* and go over TS2* without residing in the intermediate well for any appreciable time – a seemingly one step reaction. Note than no TS for directly traversing from 1* to INT2* was found.

1* 0.0
TS1* 12.9	INT1* 7.1
TS2* 8.2	INT2* -15.4

Figure 1. CASSCF(10,10)/6-31G(d) geometries and CASMP2 energies in kcal mol^-1.

Now in a follow-up study, Houk and co-workers⁴ performed trajectories analysis on the M06-2x/6-31G(d) PES. A total of 256 trajectories were initiated at TS1* and 241 ended at INT2* within 1500fs. Of these, 24 trajectories resided for less than 60fs within the region of INT1, a time less than a C-C vibration. Furthermore, the lifetime of INT1 that is predicted by RRKM is much longer (about 500fs) than what is observed in the trajectories (about 200 fs). Thus, there is significant dynamic effects in this excited state rearrangement, though INT1 is always sampled.

References

(1) Zimmerman, H. E.; Grunewald, G. L. "The Chemistry of Barrelene. III. A Unique Photoisomerization to Semibullvalene," J. Am. Chem. Soc. 1966, 88, 183-184, DOI: 10.1021/ja00953a045.

(2) Zimmerman, H. E.; Binkley, R. W.; Givens, R. S.; Sherwin, M. A. "Mechanistic organic photochemistry. XXIV. The mechanism of the conversion of barrelene to semibullvalene. A general photochemical process," J. Am. Chem. Soc. 1967, 89, 3932-3933, DOI: 10.1021/ja00991a064.

(3)  Matute, R. A.; Houk, K. N. "The Triplet Surface of the Zimmerman Di-π-Methane Rearrangement of Dibenzobarrelene," Angew. Chem. Int. Ed. 2012, 51, 13097-13100, DOI: 10.1002/anie.201208002.

(4) Jiménez-Osés, G.; Liu, P.; Matute, R. A.; Houk, K. N. "Competition Between Concerted and Stepwise Dynamics in the Triplet Di-π-Methane Rearrangement," Angew. Chem. Int. Ed. 2014,
53, 8664-8667, DOI: 10.1002/anie.201310237.

InChIs

1: InChI=1S/C16H12/c1-2-6-12-11(5-1)15-9-10-16(12)14-8-4-3-7-13(14)15/h1-10,15-16H
InChIKey=VWDKVBGOVYWYFZ-UHFFFAOYSA-N

2: InChI=1S/C16H12/c1-3-7-11-9(5-1)13-10-6-2-4-8-12(10)15-14(11)16(13)15/h1-8,13-16H
InChIKey=RATAQXOLJVRERC-UHFFFAOYSA-N

Demonstrating the occurrence of non-statistical dynamics generally has been accomplished through trajectory studies. These trajectory studies are often quite computationally demanding, requiring many trajectories, often of long duration, with molecules that are typically not small! Schmittel and co-workers present a case where their evidence for non-statistical dynamics rests not on trajectory studies but a combination of experimental product distributions and free energy of activation computations.¹

For the Schmittel C²-C⁶ cyclization taking 1 into 5¸Schmittel has located no concerted transition state, but rather two different transition states 2 and 2’, leading to a common intermediate diradical 3. Then there are two different transition states 4 and 4’ leading to the two regioisomeric products 5 and 5’. The BLYP/6-31G* structures and relative free energies are shown in Figure 1.

1 0.0
2 19.4	2’ 20.2
3 13.3
4 16.5	4’ 15.4
5 -6.3	5’ -14.3

Figure 1. BLYP/6-31G*geometries and relative free energies (kcal mol^-1) of the critical points along the reaction 1 → 5.

If transition state theory (TST) holds here, the rate limiting step is the first set of transition states, and the product distribution should be dictated by the second set of transition states. Since 4’ is lower in energy than 4, TST predicts that 5’ should be the major product. However, the experiments show that the ratio 5:5’ ranges from 1.48 at 30 °C to 1.65 at 60 °C, with the ratio decreasing a bit at higher temperatures still.

Examination of the potential energy surfaces in the neighborhoods of the transition states and the intermediate show a couple of interesting features. First, there is a large barrier separating 2 and 2’ and this precludes the concerted pathway. Second, the minimum energy path forward from 2 requires a sharp turn to proceed to the intermediate 3. Schmittel suggests that this surface supports the notion of some direct reaction paths from 2 avoiding the intermediate 3 and directly over transition state 4’. Schmittel offers a simple formula for predicting the percentage of the products formed from a non-statistical pathway:

X_NSQ₁ + X_SQ₂ = Q_exp

where X_NS is the mole fraction following non-statistical pathways and X_S is the fraction following a statistical pathway and Q_exp is the experimental mole ratio and Q₁ is the partitioning at the first set of TSs and Q₂ is the partitioning at the second set of TSs. While this approach is certainly much simpler than performing molecular dynamics, it does require experimental values. According to this model, the above reaction follows non-statistical dynamics about 75% of the time.

References

(1) Samanta, D.; Rana, A.; Schmittel, M. "Quantification of Nonstatistical Dynamics in an Intramolecular Diels–Alder Cyclization without Trajectory Computation," J. Org. Chem. 2014, 79, 2368-2376, DOI: 10.1021/jo500035b.

InChIs

1: InChI=1S/C28H29NSi/c1-29(2)27-17-11-16-26(22-27)28(30(3,4)5)21-20-25-15-10-9-14-24(25)19-18-23-12-7-6-8-13-23/h6-17,20,22H,1-5H3
InChIKey=CKQXQJAGCGSOOP-UHFFFAOYSA-N

5: InChI=1S/C28H29NSi/c1-29(2)24-17-11-16-22-27(24)25(19-12-7-6-8-13-19)26-21-15-10-9-14-20(21)18-23(26)28(22)30(3,4)5/h6-17H,18H2,1-5H3
InChIKey=OFALZDSJOVLMHZ-UHFFFAOYSA-N

5′: InChI=1S/C28H29NSi/c1-29(2)21-15-16-23-24(18-21)28(30(3,4)5)25-17-20-13-9-10-14-22(20)27(25)26(23)19-11-7-6-8-12-19/h6-16,18H,17H2,1-5H3
InChIKey=UQRNTADMKHTLNR-UHFFFAOYSA-N

While the [2-3]-sigmatropic rearrangement is well known and understood as allowed under the Woodward-Hoffmann rules, [1,2]-sigmatropic are much more rare, perhaps because they are forbidden by the same orbital symmetry arguments. It is perhaps surprising that these two rearrangements may sometimes be found in competition. Singleton has applied many of his tried-and-true techniques, namely, careful normal abundance kinetic isotope effect (KIE) analysis and molecular dynamics computations, to this problem.¹

Reaction 1 takes place exclusively through a [2,3]-rearrangement; the principle evidence is the lack of any crossover reaction. However, the slightly more substituted analogue shown in Reaction 2 gives rise to two products: that obtained from a [2,3]-rearrangement 6 and that obtained from a [1,2]-rearrangement 7.

The KIE for the rearrangement of 2 is large for the carbon breaking the bond with nitrogen, while it is small at the carbons that are forming the new bond. This becomes a metric for judging the transition state obtained with computations. With the computed TS and canonical variational transition state theory (VTST) including small curvature tunneling, the KIE can be computed from a computed structures and frequencies. This imposes a range of reasonable distances for the forming C-C bond of 2.6-2.9 Å – much longer that a typical distance in the TS of similar pericyclic reactions.

Crossover experiments for Reaction 2 are understood in terms of a reaction model whereby some fraction of the reactants undergo a concerted rearrangement to form 6, and 7 is formed by first breaking the C-N bond, forming two radicals, that either recombine right away or form isolated radicals that then collapse to product.

The interesting twist here is that one would expect two different transition states, one for the concerted process 8 and one to cleave the bond 9. Both do exist and are shown in Figure 1. However, VTST predicts that the concerted process should be 25-50 times faster than cleavage, and that does not match up with experiments. Amazingly, molecular dynamics trajectories started from the concerted TS 8 leads to cleavage about 20% of the time using UMO6-2X with a variety of basis sets. Thus, as Singleton has noted many times before, a single TS is crossed that leads to two different products! An argument based on entropy helps explain why the second (cleavage) pathway is viable.

8

9

Figure 1. UMO6-2x/6-31G* optimized structures of TS 8 and 9.

References

(1) Biswas, B.; Collins, S. C.; Singleton, D. A. "Dynamics and a Unified Understanding of Competitive [2,3]- and [1,2]-Sigmatropic Rearrangements Based on a Study of Ammonium Ylides," J. Am. Chem. Soc. 2014, 136, 3740-3743, DOI: 10.1021/ja4128289.

I think most organic chemists hold dear to their hearts the notion that selectivity is due to crossing over different transition states. Readers of my book and this blog know of the many examples where this notion simply is not true (see here). This post discusses yet another example taking place in a seemingly simple reaction.

Singleton has examined the nucleophilic substitution reaction of 1 with sodium tolylsulfide.¹ The mono substitution gives potentially two different stereoproducts 2 and 3. The experimental ratio of these products 2:3 is 81:19. (Note that things are a bit more complicated because disubstitution can also occur, but this has been factored into the product ratio.)

Based on previous literature, this reaction is likely to proceed in a concerted fashion, and so one might anticipate running computations to locate a transition state leading to 2 and a transition state leading to 3. In fact, Singleton finds six different TSs (the lowest energy TS 4 is shown in Figure 1), all within 2 kcal mol^-1 of each other at PCM(ethanol)/B3LYP/6-31+G**. However, the intrinsic reaction coordinate going forward from each of these six TSs leads solely to 2; no TS could be located that connects to 3! (Computations were also performed at PCM(ethanol)/M06-2x/6-31+G** which give very similar results.) Classical transition state theory would lead
one to conclude that only 2 should be formed, inconsistent with experiment.

4

5

Figure 1. PCM/B3LYP/6-31+G** optimized structures of TSs 4 and 5.

Furthermore, no intermediate could be located. This is consistent with a concerted mechanism. A second transition state was located which interconverts 2 and 3 with the involvement of a chloride – a sort of addition/rotation/elimination process. This TS 5 is also shown in Figure 1.

A direct dynamics study was performed, and 197 trajectories were computed. Of these, 185 trajectories went to product: 156 to 2 and 29 to 3, for a ratio of 84:16 – in amazing agreement with experiment! The product selectivity is due entirely to dynamic effects. In fact, it is one vibrational mode that dictates the product distribution. Essentially, the nature of the rotation about the C=C bond differentiates the eventual route, with a clockwise rotation leading always to 2 and a counterclockwise rotation leading about a third of the time to 3.

References

(1) Bogle, X. S.; Singleton, D. A. "Dynamic Origin of the Stereoselectivity of a Nucleophilic Substitution Reaction," Org. Lett., 2012, 14, 2528-2531, DOI: 10.1021/ol300817a.

InChIs

1: InChI=1S/C4H4Cl2O/c1-3(7)2-4(5)6/h2H,1H3
InChIKey=NXDUHPYJFYSBCT-UHFFFAOYSA-N

2: InChI=1S/C11H11ClOS/c1-8-3-5-10(6-4-8)14-11(12)7-9(2)13/h3-7H,1-2H3/b11-7-
InChIKey=NCXXSKTZGJETLW-XFFZJAGNSA-N

3: InChI=1S/C11H11ClOS/c1-8-3-5-10(6-4-8)14-11(12)7-9(2)13/h3-7H,1-2H3/b11-7+
InChIKey=NCXXSKTZGJETLW-YRNVUSSQSA-N

Once again the Singleton group reports experiments and computations that require serious reconsideration of our notions of reaction mechanisms.¹ In this paper they examine the reaction of dichloroketene with labeled cis-2-butene. With ¹³C at the 2 position of 2-butene, two products are observed, 1 and 1’, in a ratio of 1’:1 = 0.993 ± 0.001. This is the opposite what one might have imagined based on the carbonyl carbon acting as an electrophile.

The first interesting item is that B3LYP/6-31+G** fails to predict the proper structure of the transition state. It predicts an asymmetric structure 2, shown in Figure 1, while MPW1k/6-31+G**, M06, and MP2 predict a C_s transition structure 3. The C_s TS is confirmed by a grid search of M06-2x geometries with CCSD(T)/6-311++G88/PCM(CH₂Cl₂) energies.

2

3

Figure 1. Optimized TSs 2 (B3LYP/6-31+G**) and 3 (MPW1K/6-31+G**).

The PES using proper computational methods is bifurcating past TS 3, falling downhill to product 1 or 1’. Lying on the C_s plane is a second transition state that interconverts 1 and 1’. On such a surface, conventional transition state theory would predict equal amounts of 1 and 1’, i.e. no isotope effect! So they must resort to a trajectory study – which would be impossibly long if not for the trick of making the labeled carbon super-heavy – like ²⁸C,⁴⁴C, ⁷⁶C and ¹⁴⁰C and then extrapolating back to just ordinary ¹³C. These trajectories indicate a ratio of 1’:1 of 0.990 in excellent agreement with the experimental value of 0.993.

Interestingly, most trajectories recross the TS, usually by reaching into the region near the second TS. However, the recrossing decreases with increasing isotopic mass, and this leads to the isotope effect. It turns out the vibrational mode 3 breaks the C_s symmetry; movement in one direction along mode 3 has no mass dependence but in the opposite direction, increased mass leads to decreased recrossing – or put in another way, in this direction, increased mass leads more often to product.

But one can understand this reaction from a statistical point of view as well. If one looks at the free energy surface, there is a variational TS near 3, but then there is a second set of variational transition states (one leading to 1 and one to 1’) which are associated with the formation of the second C-C bond. In a sense there is an intermediate past 3 that leads to two entropic barriers, one on a path to 1 and one on the path to 1’. RRKM using this model gives a ratio of 0.992 – again in agreement with experiment! It is as Singleton notes “perplexing”; how do you reconcile the statistical view with the dynamical (trajectory) view? Singleton has no full explanation.

Lastly, they point out that a similar situation occurs in the organocatalyzed Diels-Alder reaction of MacMillan shown below.² (This reaction is also discussed in a previous post.) Now Singleton finds that the “substituent effects, selectivity, solvent effects, isotope effects and activation parameters” are all dictated by a second variational TS far removed from the conventional electronic TS.

References

(1) Gonzalez-James, O. M.; Kwan, E. E.; Singleton, D. A., "Entropic Intermediates and Hidden Rate-Limiting Steps in Seemingly Concerted Cycloadditions. Observation, Prediction, and Origin of an Isotope Effect on Recrossing," J. Am. Chem. Soc. 2012, 134, 1914-1917, DOI: 10.1021/ja208779k

(2) Ahrendt, K. A.; Borths, C. J.; MacMillan, D. W. C., "New Strategies for Organic Catalysis: The First Highly Enantioselective Organocatalytic Diels-Alder Reaction," J. Am. Chem. Soc. 2000, 122, 4243-4244, DOI: 10.1021/ja000092s.

InChIs

2-butene: InChI=1/C4H8/c1-3-4-2/h3-4H,1-2H3/b4-3-
InChIKey=IAQRGUVFOMOMEM-ARJAWSKDBO

Dichloroketene: InChI=1/C2Cl2O/c3-2(4)1-5
InChIKey=TVWWMKZMZALOFP-UHFFFAOYAY

1 (no isotope): InChI=1/C6H8Cl2O/c1-3-4(2)6(7,8)5(3)9/h3-4H,1-2H3/t3-,4+/m0/s1
InChIKey=BAEYWHUXGUIZSP-IUYQGCFVBH

The roaming mechanism has gained some traction as a recognizable model.^1,2 This mechanism involves typically the near complete dissociation of a molecule into two radical fragments. But before they can completely separate they form a loose complex on a flat potential energy surface. The two fragments can then wander about each other (the “roaming” part of the mechanism), eventually finding an alternative exit channel. The first example was the dissociation of formaldehyde which forms the complex H + CHO.³ The hydrogen atom roams over to the other side of the HCO fragment and then abstracts the second hydrogen atom to form H₂ and CO – with the unusual signature of a hot H₂ molecule and CO in low rotational/vibrational states.

The photodissociation of nitrobenzene is now suggested to also follow a roaming pathway.⁴ Bimodal distribution is found for the NO product channel. There is a slow component with low J and a fast component with high J. This suggests two different operating mechanisms for dissociation.

G2M(CC1)/UB3LYP/6-311+G(3df,2p) computations provide the two mechanisms. Near dissociation to phenyl radical and NO₂ can lead to a roaming process that eventually leads to recombination to form phenyl nitrite, which can then dissociate to the slow NO product. The fast NO product is suggested to come from rearrangement of nitrobenzene to phenylnitrite on the triplet surface, again eventually leading to loss of NO, but with high rotational excitation.

References

(1) Herath, N.; Suits, A. G., "Roaming Radical Reactions," J. Phys. Chem. Lett. 2011, 2, 642-647, DOI: 10.1021/jz101731q

(2) Bowman, J. M.; Suits, A. G., "Roaming reactions: The third way," Phys. Today 2011, 64, 33-37, DOI: 10.1063/PT.3.1330

(3) Townsend, D.; Lahankar, S. A.; Lee, S. K.; Chambreau, S. D.; Suits, A. G.; Zhang, X.; Rheinecker, J.; Harding, L. B.; Bowman, J. M., "The Roaming Atom: Straying from the Reaction Path in Formaldehyde Decomposition," Science 2004, 306, 1158-1161, DOI: 10.1126/science.1104386.

(4) Hause, M. L.; Herath, N.; Zhu, R.; Lin, M. C.; Suits, A. G., "Roaming-mediated isomerization in the photodissociation of nitrobenzene," Nat. Chem 2011, 3, 932-937, DOI: 10.1038/nchem.1194

InChI

Nitrobenzene: InChI=1/C6H5NO2/c8-7(9)6-4-2-1-3-5-6/h1-5H
InChIKey=LQNUZADURLCDLV-UHFFFAOYAA

The [1,5]-H migration in cyclopentadiene seems like it should be a very ordinary reaction. A molecular dynamics study by Carpenter at first glance appears to confirm this notion.¹ Trajectories studies show that the ratio of endo:exo migration is very close to 1:1, suggesting, as expected, statistical behavior. However, inspection of the time dependence of the endo to exo migration shows oscillatory behavior. This oscillation corresponds to the B₁ vibration that effectively flips the methylene group through the ring plane and interchanges the exo and endo hydrogens. The hydrogen preferentially migrates from the endo position, with the ring bent by typically 10°, a point far from the computed [1,5]-H migration transition state (which is planar).

Differential damping this B₁ vibration should then lead to variable endo:exo ratios, and Carpenter suggests that performing this reaction in the gas phase and in solution with different solvent viscosities should exhibit such a variable ratio. The experiment awaits an experimenter!

Once again the take-home message is that dynamics matter, even in seemingly simple and well-understood processes. Reactions can take place far from the nominal transition state and the consequences can be significant.

References

(1) Goldman, L. M.; Glowacki, D. R.; Carpenter, B. K., "Nonstatistical Dynamics in Unlikely Places: [1,5] Hydrogen Migration in Chemically Activated Cyclopentadiene," J. Am. Chem. Soc. 2011, 133, 5312-5318, DOI: 10.1021/ja1095717

Reactions whose outcomes depend on dynamic processes is a major theme of my book and this blog. The recent study of the reaction of a nucleophile (hydroxide) with bromoacetophenones adds yet another case for post-transition state product determination.

Itoh and Yamataka have examined the reaction of hydroxide with substitutes α-bromoacetophenones 1.¹ The nucleophile can attack at the carbonyl carbon or the α-carbon, though both lead ultimately to the same product, as shown in Scheme 1.

Scheme 1

B3LYP/6-31+G* computations of the reaction surface with a variety of different substituents on the phenyl ring of 1 located in all cases a single transition state for the two different reactions (addition and substitution). This TS is shown in Figure 1 for the parent case (X=H).

Figure 1. The single transition state for the addition and substitution reaction of 1 and hydroxide.

Tracing the IRC forward leads to either the carbonyl addition product or the substitution product, and which path is traced depends to some extent on the nature of the substituent. Most intriguing is that trajectories initiated at the transition state lead to both products. So once again, we see a case where a single transition state leads to two products, and product selectivity is determine by the dynamics – the initial conditions at the TS dictate which of the two products is eventually obtained.

References

(1) Itoh, S.; Yoshimura, N.; Sato, M.; Yamataka, H., "Computational Study on the Reaction Pathway of α-Bromoacetophenones with Hydroxide Ion: Possible Path Bifurcation in the Addition/Substitution Mechanism," J. Org. Chem., 2011, 70, 8294–8299, DOI: 10.1021/jo201485y

In a previous post, I described the work of Singleton on a simple hydroboration reaction. He found less regioselectivity than predicted by transition state theory. Further, trajectory computations suggested that dynamic effects were at play, and that some non-selective fast reactions were leading to the lower regioselection.

Pilling offers an alternative explanation based solely on RRKM (statistical) theory.¹ (Actually what is utilized is the stochastic energy grained master equation.) What he suggests is that there are hot intermediates (formed of a loose associate of BH₃ with propene) that react non-selectively before cooling. The cooled intermediates react very selectively (around 99%) to give the anti-Markovnikov product.

The upshot is that hydroboration – and by implication a whole lot of other seemingly ordinary chemistry – may in fact be much more complicated than we had previously thought. Standard transition state theory may not always apply, and trajectory analysis may not be enough!

References

(1) Glowacki, D. R.; Liang, C. H.; Marsden, S. P.; Harvey, J. N.; Pilling, M. J., "Alkene Hydroboration: Hot Intermediates That React While They Are Cooling," J. Am. Chem. Soc., 2010, 132, 13621-13623, DOI: 10.1021/ja105100f

Alder and co-workers have published a substantial theoretical study of potential [6+4]-cycloaddition reactions.¹ There is much too much to summarize from this study, but I highlight here an interesting result that is consistent with one of the themes of the book and blog: unusual potential energy surfaces.

They examined two [6+4]-cycloadditon routes involving 1,3,5-hexatriene with 1,3-butadiene to give 1 and 2. These products are shown in Figure 1. A competing [4+2]-cycloaddition is also possible, giving rise to 3 and 4. Interestingly, only one TS is found leading to 1/3 and one TS leading to 2/4. (These TSs are also shown in Figure 1.) This is reminiscent of many examples from the book and blog where a single TS seems to lead to 2 different products. A valley-ridge inflection point divides the surface between 1 and 3 (VRI-1), and a second valley-ridge inflection point separates 2 from 4 (VRI-2). In addition a Cope transition state (CTS1) takes 1 into 3, and a second TS (CTS2) takes 2 into 4.

TS1	TS2
1	2
CTS1	CTS2

Figure 1. B3LYP/6-31G* optimized structures of the TSs and products of the reaction of 1,3,5-hexadiene with 1,3-butadiene.¹

This type of surface requires study of the dynamics to truly predict what the outcome will be of the reaction. Unfortunately, the low barriers for the Cope rearrangements along with 3 and 4 being much more stable than 1 and 2 indicates that the [6+4] product is unlikely to be observed. Nonetheless, this is yet another example of an unexpected PES.

References

(1) Alder, R. W.; Harvey, J. N.; Lloyd-Jones, G. C.; Oliva, J. M., "Can _π6 + _π4 = 10? Exploring Cycloaddition Routes to Highly Unsaturated 10-Membered Rings," J. Am. Chem. Soc. 2010, 132, 8325-8337, DOI: 10.1021/ja1008135

InChIs

1: InChI=1/C10H14/c1-2-4-6-8-10-9-7-5-3-1/h1-4,9-10H,5-8H2/b3-1-,4-2+,10-9+
InChIKey=RBGHZLIWLPEVLM-OCXPBMDHBA

2: InChI=1/C10H14/c1-2-4-6-8-10-9-7-5-3-1/h1-4,9-10H,5-8H2/b3-1-,4-2-,10-9+
InChIKey=RBGHZLIWLPEVLM-ARMDLRMMBD

3: InChI=1/C10H14/c1-3-9-7-5-6-8-10(9)4-2/h3-5,7,9-10H,1-2,6,8H2/t9-,10-/m0/s1
InChIKey=ANOQDGNLTWJTRB-UWVGGRQHBI

4: InChI=1/C10H14/c1-3-9-7-5-6-8-10(9)4-2/h3-5,7,9-10H,1-2,6,8H2/t9-,10+/m1/s1
InChIKey=ANOQDGNLTWJTRB-ZJUUUORDBZ